第1页 / 共6页
第2页 / 共6页
第3页 / 共6页
第4页 / 共6页
第5页 / 共6页
第6页 / 共6页
IEEE 802.11ax On Performance of MultiAntenna Technologies with L....pdf
IEEE 802.11ax: On Performance of Multi-
Antenna Technologies with LDPC Codes
Roger Pierre Fabris Hoefel
Electrical Engineering Department
Federal University of Rio Grande do Sul (UFRGS)
Porto Alegre, RS, Brazil
roger.hoefel@ufrgs.br
Abstract—The implementation of low-density parity-check (LDPC)
codes will be a mandatory feature in the 2019 IEEE 802.11ax
amendment, the sixth generation of wireless local area networks
(WLANs) for frequencies below 6 GHz. Orthogonal frequency
division multiplexing multi-user multiple-input multiple-output
(OFDM MU-MIMO) technologies for both downlink and uplink
have been specified in Task Group (TG) 802.11ax meetings to
improve the spectrum and area efficiency in ultra-dense WLANs.
In this paper, we compare the performance of binary convolutional
codes (BCC) and LDPC codes using different configurations of
multi-antenna technologies taking into account both hardware and
system impairments. We have concluded that on the most study
cases, the implementation of LDPC codes in the IEEE 802.11ax
physical layer allows power gains between 2.5 and 4.0 dB in relation
to BCC with soft-decision Viterbi decoding.
Keywords—802.11ax; LDPC, BCC; Multi-User MIMO.
I. INTRODUCTION
The optional implementation of low-density parity-check
(LDPC) codes was specified in the 2007 IEEE 802.11n
amendment, where single-user multiple-input multiple-output
(SU-MIMO) technologies were introduced by the first time in
wireless local area networks (WLANs) [1, p.164]. Notice that
the implementation of binary convolutional codes (BCC) is
mandatory in the 802.11 standards. The LDPC codes remained
as an optional feature in the 2013 IEEE 802.11ac amendment,
the 5th generation of WLANs, where the downlink (DL) multi-
user (MU) MIMO technology was specified to improve the
network throughput. The IEEE Task Group (TG) 802.11ax,
lauched in 2014, aims to improve spectrum and area throughput
of ultra-dense WLANS deployed in both indoor and outdoor
environments using frequencies below 6 GHz. Both downlink
and uplink (UL) MU-MIMO and orthogonal frequency division
multiple access (OFDMA) are essential technologies to achieve
the ambitious targets defined by IEEE TG 802.11ax [2]. At this
moment, the TG 802.11ax has been working in the resolutions
to improve the Draft 2.0, released in October 2017, since its
approval was failed in November 2017 [3]. However, there is a
consensus that the implementation of LDPC codes will be
mandatory in 2019 802.11ax amendment [2], and researchers
from industry and academia have been presented several studies
about this topic in TGax meetings (e.g., LDPC codes for 1024-
QAM [4]).
We have been developing research activities related to the
effects of hardware impairments on the performance of
orthogonal frequency division multiplexing (OFDM) UL MU-
MIMO technology in the IEEE 802.11ax physical layer (PHY).
In reference [5], we have concluded, based on extensive
simulation results, that the joint effects of in-phase and
quadrature (IQ) imbalance and differences on the received
power at the access point (AP) can affect dramatically the
performance of UL MU-MIMO 802.11ax PHY. In reference [6],
we implement a joint power control (PC) and time-domain IQ
imbalance mitigation scheme that counterbalances the effects of
IQ hardware impairments on the UL MU-MIMO 802.11ax PHY
performance.
Analyze, design and optimization of LDPC for WLANs have
been extensively researched in academia and industry since the
specification of 2007 IEEE 802.11n amendment [1, p. 164].
However, we strongly believe that we can contribute with our
wireless
research community by developing a unified
performance evaluation of the IEEE 802.11ax PHY with either
BCC or LDPC codes using different multi-antenna
technologies: spatial multiplexing (SM) SU-MIMO; DL MU-
MIMO and UL MU-MIMO. One main novel contribution of this
paper
the
implementation of LDPC codes in OFDM UL MU-MIMO
802.11ax PHY with hardware and system impairments. Finally,
we mention that the design of techniques to mitigate the effects
of hardware impairments on the 802.11ax PHY performance is
still a topic of intensive research in the Wi-Fi community [7-8].
The remaining of this paper is organized as follows: Section II
succinctly describes aspects related to the implementation of
LDPC codes in 802.11 WLANs. Section III presents simulation
results that allow a first order validation of our IEEE
802.11ac/ax PHY simulator. Section
the
performance of 802.11ax PHY over a set of significant scenarios
with BCC and LDPC codes. Section V concludes this paper.
issues and drawbacks on
IV analyzes
is related
to
the
II. LOW DENSITY PARITY CHECK CODES IN 802.11 WLANS
The LDPC codes specified in 802.11 amendments support
block lengths of 648 bits, 1296 bits and 1944 bits [1, p. 167]. The
LDPC encoding process fits the payload bits into an integer
number of OFDM symbols and an integer number of LDPC code
words using the following steps [1, pp. 165-175]:
1. Determine the minimum number of OFDM symbols based on
the payload length and the number of bits per subcarrier (SC).
2. Determine the number of code words and the LDPC code
word length using a table look up procedure.
3. Determine the number of shortening bits, where shortening is
defined as the procedure of inserting zeros after the payload
bits before computing the parity bits.
4. Generate the parity bits per each code word using the LDPC
802.11 parity check matrices [1, p. 177]. In this paper, we
implement a computational efficient recursive encoding
procedure proposed in [9] for 802.11n systematic LDPC
codes. The shortening bits are deleted from each code word
after the parity bits are calculated.
5. Puncture the parity bits if the total number of coded bits is
159
greater than the total number of coded bits that fit in all OFDM
symbols. Decision rules are specified to create one more
OFDM symbol (which that reduces or even eliminates the
need of puncturing) in order to avoid performance degradation
due to excessive puncturing. On the other hand, if puncturing
is not necessary, then it is performed the repetition of the
coded bits to fill all the bits into the OFDM symbols.
6. Perform the concatenation of the LDPC code words;
demultiplex the code word bits into spatial streams (stream
parsing) and modulate the coded bits into symbols. Notice that
interleaving is not implemented for the LDPC codes due to
their intrinsic pseudo-randomness that avoids burst errors.
III. IEEE 802.11AX SIMULATOR
Table I shows the main parameters and characteristics of the
IEEE 802.11ax/ac simulator that we have been developing [10].
In this paper, we implement soft-decision Viterbi decoding for
BCC, while the LDPC codewords are decoded using a message
passing algorithm, implemented using the log-domain sum-
product algorithm. The number maximum of iterations is set to
100.
Table II reports the modulation and code schemes (MCS)
whose performance is analyzed in this research. Notice that for
LDPC codes, the code rate of the MCS can be different from the
native code rate shown in Tab. II due to the operations of
shortening, puncturing and repetition. However, as the number
of payload bits increases, there is a minor difference between the
native code rate and the effective code rate for LDPC codes. On
the other hand, the MCS determines the code rate for BCC.
TABLE I. Parameters and characteristics of the IEEE 802.11ax simulator.
Parameter
Carrier
Frequency
Bandwidth
(BW)
GI Length
Modulation
Channel Codes:
1. BCC
2. LDPC
Value
5.25 GHz
Parameter
MCS
20 MHz, 40 MHz,
80 MHz
800 ns
BPSK, QPSK,
16-QAM, 64-QAM,
Number of
Spatial Streams
Synchronization
MIMO Channel
Estimation
Value
0-9
1 to 8
Auto-Correlation
Least Squares (LS)
[1, p. 98]
256-QAM
Code rate:
r=1/2, r=2/3, r=3/4,
r=5/6
Channel
Decoder
Hard and Soft-
Decision Viterbi
Decoding,
LDPC Soft-Decision
TABLE II. Characteristics of the MCS analyzed in this paper.
MCS
0
1
2
3
Mod
BPSK
QPSK
QPSK
16-QAM
Code Rate
MCS
1/2
1/2
3/4
1/2
4
5
6
7
Mod
16-QAM
64-QAM
64-QAM
64-QAM
Code Rate
3/4
2/3
3/4
5/6
=
∙ ,
In this paper, the signal-to-noise ratio (SNR), assuming a
normalized average power at the channel output, is defined as the
ratio of signal power to noise power at the output of each receive
antenna:
=
where is the energy per OFDM symbol available to use in
all spatial streams (SS) at the transmitter and is the number of
prefix length (CP) length are denoted by and ,
+ samples. In our baseband discrete time simulator, the
respectively. Notice that each OFDM symbol is transmitted using
transmit antennas. The fast Fourier transform (FFT) and cyclic
variance of the additive complex circular symmetric Gaussian
noise (CCSGN) random variable (r.v.) is modelled by No, which
(1)
(2)
,
where the number of bits per subcarrier (modulation cardinality),
is the one side power spectral density (PSD) of the CCSGN
random process.
The energy per bit at each SS is given by
=
and the code rate are denoted by and , respectively. The
and , respectively. The last two terms on the right of
The SNR as a function of the SNR per bit ⁄
, using (2) in
= +
Nfft
(2) model, respectively, the overhead necessary for the CP and
reference signals (pilots).
∙( ).
number of SC used for transport data and pilots are labeled as
(1), can be expressed as follows:
(3)
resulting
In this research, we shall show simulation results for the
following channels: (1) TGac B channel (multipath channel with
low frequency selectivity); (2) TGac D channel (highly
frequency selective multipath channel) [1, p. 39, pp. 57-58].
Both channels present spatial correlation at both transmitter and
receiver sides of the link. The MIMO channel defined as
[nt,nr,K,nss] has the following characteristics: (1) nt is the
number of transmit antennas; (2) nr denotes the number of
receive antennas; (3) K is the number of stations (STAs)
accessing the channel simultaneously; (4) nss is the number of
SS transmitted (received) per STA over the UL (DL) MIMO
channels.
A. Hardware and System Impairments
In the following, we describe the hardware and system
impairments investigated in this paper: phase noise (PN); IQ
imbalance; relative carrier frequency offset (CFO); differences
on the delay and average received power at the AP.
The PN hardware impairment for frequencies below 6 GHz is
modelled according with the specified by the TGax 802.11ax
[11, p. 7]. The PSD at direct current (DC) is specified as -100
dBc/Hz,
impairment must be modeled at both transmitter and receiver.
All the simulation results shown in this paper take into account
the PN effects on the system performance.
The IQ imbalance is modeled by the gain error Ia and phase
mismatch Ip between the in-phase and quadrature components
using the analytical model defined in [12]. The IQ imbalance is
constant in all subcarriers, i.e., it is non-frequency selective.
Single-side band (SSB) suppression of -30 dBc is achievable if
the radio-frequency (RF) analog front-end has a gain imbalance
of 0.5 dB and phase imbalance of 1o [13]. In this paper, we
investigate the effects of IQ imbalance on the performance of
UL MU-MIMO 802.11ax PHY.
The difference on the average received power at the AP among
the STAs in uplink transmissions is denoted by ΔP, where ΔP=
x dB means that half of the clients are x dB weaker than the other
is modelled assuming that half of the clients have extra delay
in PSD(∞)=−130 dBc/Hz. The PN
half [14].
The asynchronous reception through UL MU-MIMO channels
with relation to (w.r.t.) the other half [14].
The mitigation of the CFO is more challenging for uplink
transmissions since each client can have a different impairment
(relative CFO) due to the multipoint to point multiple access.
160
symbols at nth sample for the uth STA without CFO and IQ
The normalized CFO of the uth STA is defined by
= ,
Notice that the correction of the common CFO that impinges
equally all clients in both downlink and uplink transmissions can
be mitigated without the need of pre-compensation scheme at
the transmitter (i.e., STAs for UL MU-MIMO) [10].
The CFO in the uplink is modelled as follows:
(5)
where Δfu and DF denote the CFO of the uth STA and the
spacing between SC, respectively [15, p. 27].
[]=,[]+,[]=∑
()[]
, (4)
where ()[]=()[]+()[] denotes the complex received
unbalancing. The sample period is denoted by .
In this paper we use the following notation for the CFO: =
& ∆ Hz means that half of the STAs have a common
normalized CFO = (see Eq. 5) plus an unnormalized relative
CFO of −∆ 2⁄ Hz and the other half of the STAs have the same
common relative CFO of = plus an unnormalized relative
CFO of +∆ 2⁄ Hz [10, 16]. We use the same specifications
maximum CFO of ±232 kHz, i.e., |ε|≅0.74 [1].
[]=,[]+,[]=,[]+10 ,
∙,[], (6)
[]=,[]+10 ,∙,[]−∙[]. (7)
The time-domain received signal with CFO and IQ imbalance
with gain Ia,dB in dB is modeled by (6). The received signal with
CFO and amplitude and phase imbalance is given by (7), where
Ip denotes the IQ phase mismatch [12].
defined in the 802.11ac amendment, i.e., SC of 312.5 kHz and
B. First-Order Validation
Fig. 1 compares our simulation results for the packet error rate
(PER) as a function of SNR in dB w.r.t the simulation results
shown in [1, p.176] for BCC (Fig. 1a) and LDPC codes (Fig. 1b),
where the following parameters are assumed: SU-MIMO TGac
D [2,2,1,2] channel; bandwidth (BW) of 20 MHz; medium access
control protocol data unit (MPDU) payload of 970 bytes. The
transmitter does not implement any precoding scheme. The
receiver implements minimum mean squared error (MMSE)
MIMO detector with realistic least squares (LS) channel state
information (CSI).
• Remark 1: The simulation of 802.11ax PHY evolve a multitude
of algorithms (e.g., time and frequency synchronization, channel
estimation, phase tracking, MIMO detector schemes, SNR
estimation on-the-flight, soft-decision metrics, BCC and LDPC
decoding algorithms) [17]. Hence, it is extremely difficult to have
an exact agreement among simulation results from different
references if the source code is not open and there is not a pre-
defined calibration procedure to validate the simulation results
obtained
the above
considerations, we claim that the results shown in Fig. 1 allows a
first-order validation of our simulation results for SU-MIMO
802.11 PHY.
from different sources. Based on
• Remark 2: The reference [1] (see pages 31-36, 118 and 123)
defines the SNR independent of the number of transmit antennas.
In this paper, we normalize the total energy per OFDM symbol
considering all transmit antennas (cf. Eq. 1). Hence, the SNR
shown in [1] must be increased by 10 (i.e., 3 dB in Fig.
1) in order to allow a consistent comparison w.r.t the simulation
results developed in this paper.
TGac D [2,2,1,2]
20 MHz
BCC: Npl=970 bytes
MCS0: Ref. [1]
MCS0: Simulation
MCS1: Ref. [1]
MCS1: Simulation
MCS3: Ref. [1]
MCS3: Simulation
MCS4: Ref. [1]
MCS4: Simulation
MCS7: Ref. [1]
MCS7: Simulation
BCC
Npl=970 bytes
LS CSI
5
10
15
20
25
SNR in dB
30
35
40
45
Fig. 1a. Binary convolutional codes.
TGac D [2,2,1,2]
20 MHz
LDPC
Npl=970 bytes
LS CSI
MCS0: Ref. [1]
MCS0: Simulation
MCS1: Ref. [1]
MCS1: Simulation
MCS3: Ref. [1]
MCS3: Simulation
MCS4: Ref. [1]
MCS4: Simulation
MCS7: Ref. [1]
MCS7: Simulation
1
0.1
R
E
P
0.01
1
0.1
R
E
P
0.01
5
10
15
20
25
30
35
40
45
SNR in dB
Fig. 1b. Low-density parity-check codes.
Fig. 1. Comparison between the PER as a function of the SNR in dB obtained
from our IEEE 802.11ac/ax simulator and the simulation results from [1]: TGac
D [2,2,1,2] channel; BW=20 MHz; MMSE MIMO receiver with LS CSI; MPDU
payload of 970 bytes.
IV. PERFORMANCE ANALYSES: LDPC VS BCC IN 802.11AX PHY
A. Effects of Bandwidth on the Performance Gain
In this section, we evaluate the effects of system bandwidth on
the performance of BCC and LDPC codes on the IEEE
802.11ac/ax PHY.
Table III shows the data rates for the MCS whose performance
is investigated in this subsection.
TABLE III. Data for SU-MIMO configuration with 2 SS. The PHY data rates
assume a guard-interval (GI) of 800 ns.
MCS
Data Rate: 2 SS
Mbps
20 MHz
80 MHz
0
1
2
3
13.0
26.0
39.0
52.0
58.5
117.0
175.5
234.0
4
5
6
7
MCS
Data Rate: 2 SS
Mbps
20 MHz
78.0
104.0
117.0
130.0
80 MHz
351.0
468.0
526.5
585.0
Fig. 2 shows the PER as a function of SNR in dB using the
same configuration of Fig. 1, except that now it is shown results
for bandwidths of 20 and 80 MHz.
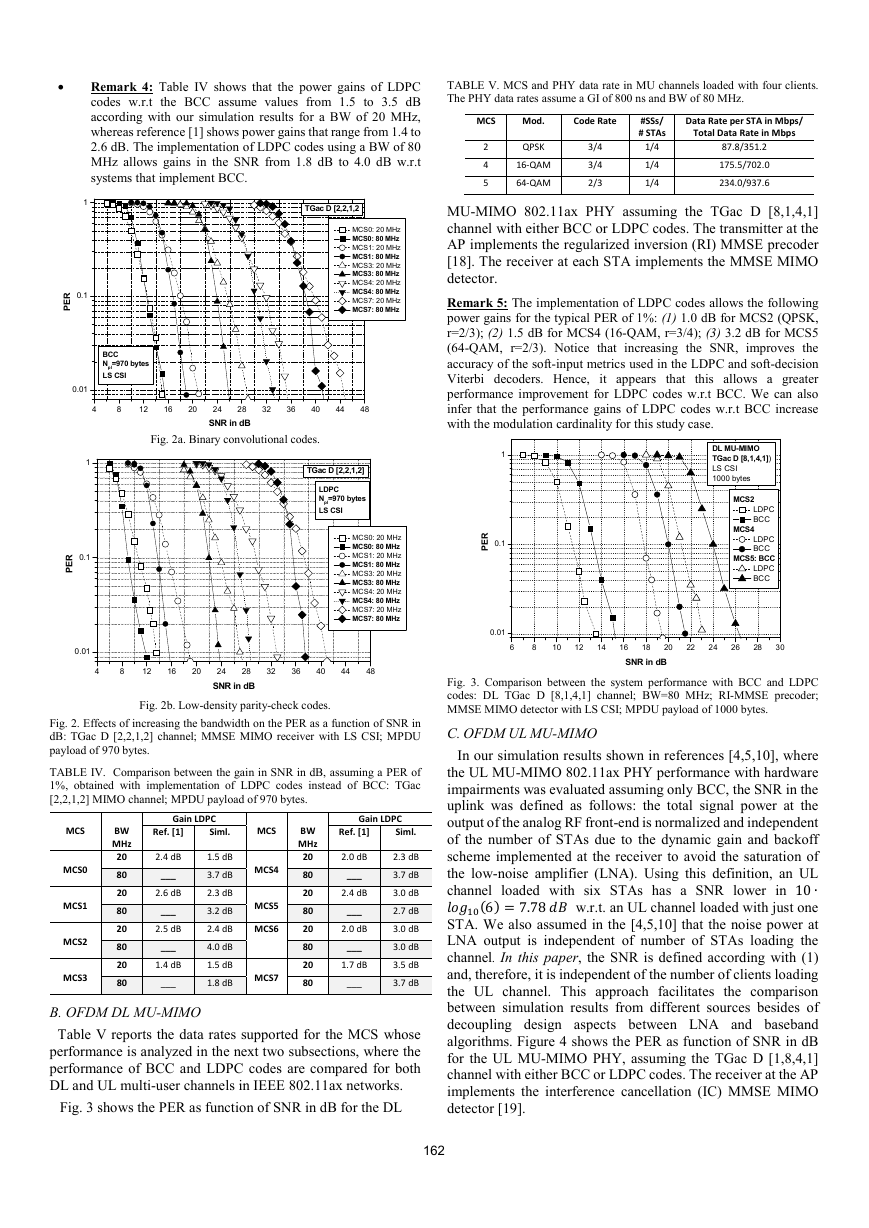
• Remark 3: The increase of frequency diversity due to the larger
bandwidth can improve the system performance for both BCC
and LDPC codes, mainly when modulation schemes with
higher cardinality are used. Notice that the power gains due to
the higher BW ranges from 0 dB (MCS0 with BCC) to 3 dB
(MCS7 for both BCC and LDPC codes).
161
1
0.1
R
E
P
0.01
1
0.1
R
E
P
0.01
1
R
E
P
0.1
TGac D [2,2,1,2]
LDPC
Npl=970 bytes
LS CSI
MCS0: 20 MHz
MCS0: 80 MHz
MCS1: 20 MHz
MCS1: 80 MHz
MCS3: 20 MHz
MCS3: 80 MHz
MCS4: 20 MHz
MCS4: 80 MHz
MCS7: 20 MHz
MCS7: 80 MHz
DL MU-MIMO
TGac D [8,1,4,1])
LS CSI
1000 bytes
MCS2
LDPC
BCC
MCS4
LDPC
BCC
MCS5: BCC
LDPC
BCC
•
Remark 4: Table IV shows that the power gains of LDPC
codes w.r.t the BCC assume values from 1.5 to 3.5 dB
according with our simulation results for a BW of 20 MHz,
whereas reference [1] shows power gains that range from 1.4 to
2.6 dB. The implementation of LDPC codes using a BW of 80
MHz allows gains in the SNR from 1.8 dB to 4.0 dB w.r.t
systems that implement BCC.
TGac D [2,2,1,2
MCS0: 20 MHz
MCS0: 80 MHz
MCS1: 20 MHz
MCS1: 80 MHz
MCS3: 20 MHz
MCS3: 80 MHz
MCS4: 20 MHz
MCS4: 80 MHz
MCS7: 20 MHz
MCS7: 80 MHz
BCC
Npl=970 bytes
LS CSI
4
8
12
16
20
28
24
SNR in dB
32
36
40
44
48
Fig. 2a. Binary convolutional codes.
TABLE V. MCS and PHY data rate in MU channels loaded with four clients.
The PHY data rates assume a GI of 800 ns and BW of 80 MHz.
MCS
2
4
5
Mod.
Code Rate
QPSK
16-QAM
64-QAM
3/4
3/4
2/3
#SSs/
# STAs
1/4
1/4
1/4
Data Rate per STA in Mbps/
Total Data Rate in Mbps
87.8/351.2
175.5/702.0
234.0/937.6
MU-MIMO 802.11ax PHY assuming the TGac D [8,1,4,1]
channel with either BCC or LDPC codes. The transmitter at the
AP implements the regularized inversion (RI) MMSE precoder
[18]. The receiver at each STA implements the MMSE MIMO
detector.
Remark 5: The implementation of LDPC codes allows the following
power gains for the typical PER of 1%: (1) 1.0 dB for MCS2 (QPSK,
r=2/3); (2) 1.5 dB for MCS4 (16-QAM, r=3/4); (3) 3.2 dB for MCS5
(64-QAM, r=2/3). Notice that increasing the SNR, improves the
accuracy of the soft-input metrics used in the LDPC and soft-decision
Viterbi decoders. Hence, it appears that this allows a greater
performance improvement for LDPC codes w.r.t BCC. We can also
infer that the performance gains of LDPC codes w.r.t BCC increase
with the modulation cardinality for this study case.
4
8
12
16
20
24
28
SNR in dB
32
36
40
44
48
Fig. 2b. Low-density parity-check codes.
Fig. 2. Effects of increasing the bandwidth on the PER as a function of SNR in
dB: TGac D [2,2,1,2] channel; MMSE MIMO receiver with LS CSI; MPDU
payload of 970 bytes.
TABLE IV. Comparison between the gain in SNR in dB, assuming a PER of
1%, obtained with implementation of LDPC codes instead of BCC: TGac
[2,2,1,2] MIMO channel; MPDU payload of 970 bytes.
Gain LDPC
Gain LDPC
MCS
MCS0
MCS1
MCS2
MCS3
BW
MHz
20
80
20
80
20
80
20
80
Ref. [1]
Siml.
MCS
2.4 dB
___
2.6 dB
___
2.5 dB
___
1.4 dB
___
1.5 dB
3.7 dB
2.3 dB
3.2 dB
2.4 dB
4.0 dB
1.5 dB
1.8 dB
MCS4
MCS5
MCS6
MCS7
BW
MHz
20
80
20
80
20
80
20
80
Ref. [1]
Siml.
2.0 dB
___
2.4 dB
___
2.0 dB
___
1.7 dB
___
2.3 dB
3.7 dB
3.0 dB
2.7 dB
3.0 dB
3.0 dB
3.5 dB
3.7 dB
B. OFDM DL MU-MIMO
Table V reports the data rates supported for the MCS whose
performance is analyzed in the next two subsections, where the
performance of BCC and LDPC codes are compared for both
DL and UL multi-user channels in IEEE 802.11ax networks.
Fig. 3 shows the PER as function of SNR in dB for the DL
0.01
6
8
10
12
14
18
16
20
SNR in dB
22
24
26
28
30
Fig. 3. Comparison between the system performance with BCC and LDPC
codes: DL TGac D [8,1,4,1] channel; BW=80 MHz; RI-MMSE precoder;
MMSE MIMO detector with LS CSI; MPDU payload of 1000 bytes.
C. OFDM UL MU-MIMO
In our simulation results shown in references [4,5,10], where
the UL MU-MIMO 802.11ax PHY performance with hardware
impairments was evaluated assuming only BCC, the SNR in the
uplink was defined as follows: the total signal power at the
output of the analog RF front-end is normalized and independent
of the number of STAs due to the dynamic gain and backoff
scheme implemented at the receiver to avoid the saturation of
the low-noise amplifier (LNA). Using this definition, an UL
channel loaded with six STAs has a SNR lower in 10∙
(6)=7.78 w.r.t. an UL channel loaded with just one
STA. We also assumed in the [4,5,10] that the noise power at
LNA output is independent of number of STAs loading the
channel. In this paper, the SNR is defined according with (1)
and, therefore, it is independent of the number of clients loading
the UL channel. This approach facilitates the comparison
between simulation results from different sources besides of
decoupling design aspects between LNA and baseband
algorithms. Figure 4 shows the PER as function of SNR in dB
for the UL MU-MIMO PHY, assuming the TGac D [1,8,4,1]
channel with either BCC or LDPC codes. The receiver at the AP
implements the interference cancellation (IC) MMSE MIMO
detector [19].
162
1
R
E
P
0.1
0.01
no CFO
no IQ
MCS2: BCC
MCS4: BCC
Ref. [16]
Sml.
Ref. [16]
Sml
Ref. [16]
Sml.
MCS5: BCC
UL MU-MIMO
TGac D [1,8,4,1])
Lest Square CSI
1000 bytes
no CFO
no IQ
MCS2: LDPC
MCS4: LDPC
Sml.
Sml
MCS5: LDPC
Sml.
1
R
E
P
0.1
0.01
TGac B [1,8,6,1]
TGac D [1,8,6,1])
MCS3: 16-QAM
1500 bytes
No IQ, ΔP= 0 dB
ΔT=0 ns
BCC
LDPC
IQ: -30 dBc
ΔP= 10 dB,PC: ON
ΔT=400 ns
IQ Mitigation
LDPC
BCC
No IQ Mitigation
LDPC
24
26
28
30
32
34
2
4
6
8
10
14
12
16
SNR in dB
18
20
22
24
26
Fig. 4. Comparison between the system performance with BCC and LDPC
codes: UL TGac D [1,8,4,1] channel; BW=80 MHz; IC-MMSE MU-MIMO
detector with LS CSI; MPDU payload of 1000 bytes.
• Remark 6: There is a good agreement between our simulations
results and the simulation results published in [16] for BCC.
• Remark 7: The implementation of LDPC codes allows the
following power gains for a PER of 1% w.r.t the 802.11ax PHY
that implements BCC: (1) 3.0 dB for MCS2 (QPSK, r=2/3); (2)
4.0 dB for MCS4 (16-QAM, r=3/4); (3) 3.2 dB for MCS5 (16-
QAM, r=2/3).
• Remark 8: When BCCs are implemented, there is a greater
demand of SNR in the DL MU-MIMO (see Fig. 3) in relation to
the UL MU-MIMO 802.1ax PHY (see Fig. 4) to obtain a target
PER of 1%: (1) 3 dB for MCS2 and MCS5; (2) 2.5 dB for MCS4.
It is assumed that the same power is available in the DL and UL,
then the power available at the transmitter per each one of the K
STAs loading the downlink channel is 10∙()=6
less than the power available for each STA accessing the channel
in the UL. Notice that the DL MU-MIMO transceiver
implements RI-MMSE precoding with 8 transmit antennas at the
AP and MMSE MIMO detector at each STA with only receive
antenna. On the other hand, the UL MU-MIMO transceiver has
only one transmit antenna, but it implements IC-MMSE MIMO
detector with 8 receive antennas.
• Remark 9: When LDPC codes are implemented, the differences
in the SNR between the DL (see Fig. 3) and UL (see Fig. 4) to
achieve a target PER of 1% are: (1) 4 dB for MCS2; (2) 6 dB for
MCS4; (3) 4.5 dB for MCS5. Hence, we have concluded that the
802.11ax PHY with LDPC codes presents a higher mismatch
between the SNR required to obtain the same performance in DL
and UL MU-MIMO w.r.t. the 802.11ax PHY that implements
BCC (as pointed out in the Remark 8).
D. OFDM UL MU-MIMO: IQ IMBALANCE AND POWER CONTROL
Here, we evaluate the joint effects of differences on the
received power and IQ imbalance on the PER of UL MU-MIMO
802.11ax PHY. We implement the time-domain IQ mitigation
scheme, power control (PC) and time-advance algorithms
described in [6], where the 802.11ax PHY performance was
analyzed with only BCC. The
IQ mitigation scheme
implemented in [6] is based on the scheme proposed in [12].
Fig. 5 shows the PER versus the SNR in dB for the UL MU-
MIMO 802.11ax PHY, considering the TGac B and TGac D
[1,8,6,1] channels for either BCC or LDPC codes considering
the following set ups: (1) without IQ imbalance; synchronous
channel (i.e., same delay for all clients) and same path loss; (2)
IQ
imbalance of -30 dBc; asynchronous channel with
propagation delay differences between the near and far end
clients of 400 ns; differences of path loss between the near and
6
8
10
12
14
16
20
18
22
SNR in dB
Fig. 5. Effects IQ imbalance impairment on the PER: MCS3; TGac B and TGac
D [1,8,6,1] channels; BW=80 MHz; IC-MMSE MU-MIMO receiver; LS CSI;
MPDU payload of 1500 bytes.
far end clients of 10 dB (ΔP=10 dB). Note that six clients
accessing the UL channel using MCS3 correspond to a network
throughput of 702 Mbps.
• Remark 10: The joint PC and IQ scheme mitigates adequately
the effects of IQ imbalance on the system performance. Observe
the catastrophic effects on the PER depicted for the TGacD
channel when the PC is operational, but the IQ mitigation scheme
is not operational.
• Remark 11: The implemented LDPC code allows an expressive
power gain w.r.t the BCC of 3 dB and 4 dB assuming the
[1,8,6,1] TGac B and D channels, respectively, when the MCS3
(16-QAM, r=1/2) is implemented.
E. OFDM UL MU-MIMO: IQ IMBALANCE AND CFO
In this item, we evaluate the coupled effects of IQ imbalance
and CFO on the PER of UL MU-MIMO 802.11ax PHY. All
results assume IQ imbalance of -30 dBc; asynchronous channel
with differences in the propagation delay between the near and
far end clients of 400 ns; no differences on the average received
power among the clients (ΔP=0 dB). The CFO is mitigated
using a frequency-domain estimation scheme coupled with a
pre-compensation scheme implemented at the clients [10,16].
Notice that the pre-compensation is necessary in the UL
transmissions since the receiver at the AP can only compensates
the common CFO (i.e., when all clients have the same CFO).
The IQ mitigation scheme must be implemented before the CFO
estimation and compensation algorithm at both AP and STAs.
Fig. 6 shows the PER versus the SNR in dB for the UL MU-
MIMO 802.11ax PHY, considering the TGac B and TGac D
[1,8,6,1] channels for either BCC or LDPC codes considering
the following set ups: (1) without CFO; (2) CFO with
parameters =0.7 & Δ=1000 .
• Remark 12: The reduction of the SNR decreases the estimation
accuracy of the CFO at the clients, which is necessary to pre-
compensate the relative CFO. This explains the power loss of 1.5
dB due to the CFO observed for the TGac B channel with LDPC
codes. On the other hand, the CFO estimation and mitigation
schemes are very effective for the medium and high values of the
SNR. The power gains due to the implementation of LDPC codes
are 2 dB and 4 dB for TGac B and D channels, respectively, for
MCS3 with CFO.
163
TGac B [1,8,6,1]
TGac D [1,8,6,1])
MCS3: 16-QAM
1500 bytes
IQ: -30 dBc
ΔT=400 ns
No CFO
LDPC
BCC
CFO
ε=0.7 & Δf=1000 Hz
LDPC
BCC
1
R
E
P
0.1
0.01
6
8
10
12
14
16
20
18
22
SNR in dB
24
26
28
30
32
34
Fig. 6. Joint effects of IQ imbalance and CFO on the PER: TGac D [1,8,6,1]
channel; BW=80 MHz; IC-MMSE MU-MIMO receiver; LS CSI; MPDU
payload of 1500 bytes.
F. OFDM UL MU-MIMO: IQ IMBALANCE, POWER CONTROL AND
CFO
In this last subsection, we analyze the coupled effects of IQ
imbalance and CFO on the PER of UL MU-MIMO 802.11ax
PHY when there is a difference of 10 dB (ΔP=10 dB) in the
average received power between one-half and the other-half of
the clients. All results assume IQ imbalance of -30 dBc and
asynchronous channel with latency difference between the near
and far end clients of 400 ns.
TGac D [1,8,6,1])
MCS3
IQ: -30 dBc
ΔT=400 ns
1
0.1
R
E
P
0.01
No CFO, Δ P= 0 dB
ε=0.7 & Δf=1000 Hz
Δ P= 0 dB, PC=OFF
All STAs
LDPC
BCC
LDPC
BCC
Δ P= 10 dB, PC=ON
Lower Path Loss
Higher Path Loss
LDPC
BCC
LDPC
BCC
16
18
20
22
24
28
26
SNR in dB
30
32
34
36
38
40
Fig. 7. Joint effects of IQ imbalance and relative CFO on the PER when there
are differences on the average received power among the clients: TGac D
[1,8,6,1] channel; BW=80 MHz; IC-MMSE MU-MIMO receiver; LS CSI;
MPDU payload of 1500 bytes
•
Remark 13: For the BCC, there is no power loss for the clients
with higher average received power due to the accurate CFO pre-
compensation scheme implemented at the clients. However, for
the LDPC code, a power loss of 1.8 dB for the clients with higher
average power is observed since the clients can operate with a
lower SNR to achieve a target PER (which reduces the accuracy
of CFO estimation scheme used to pre-compensate the CFO)
w.r.t the clients that implement BCC.
Remark 14: For the BCC, there is a power loss of 3.8 dB for the
clients received with lower average power. For the LDPC code,
there is a dramatic power loss of 6 dB due to the inaccurate CFO
pre-compensation scheme. At this moment, we are researching
solutions to solve the observed performance dependence with the
received power when there is CFO: (1) to implement a PC
scheme in the downlink, which allows improving the CFO
estimation by the clients; (2) to design CFO estimation
algorithms with less sensibility w.r.t. the received power.
•
V. CONCLUSIONS
We first specified the main objective of this paper: a
comparative performance assessment between BCC and LDPC
codes when these codes are implemented in the IEEE 802.11ax
PHY with multi-antenna technologies. Second, we summarized
the LDPC encoding process in 802.11 WLANs. Third, we
described and validated an 802.11ac/ax PHY simulator. In the
following, we presented an embracing set of simulation results
for SU-MIMO, DL and UL MU-MIMO that show that LDPC
codes can provide power gains w.r.t. BCC between 2.0 and 4.0
dB. Finally, we have concluded that is fundamental to design
UL and DL power control schemes to avoid performance
degradation in the UL MU-MIMO 802.11ax PHY impaired with
CFO since a relatively high SNR is demanded to estimate the
relative CFO at the clients to pre-rotate the transmitted symbols.
On the other hand, we have concluded that only DL power
control coupled with IQ mitigation scheme is necessary to avoid
performance losses due to IQ imbalance in UL MU-MIMO since
the critical correction IQ correction is carried out at the receiver.
REFERENCES
[1] E. Perahia and R. Stacey, Next Generation Wireless LANS: 802.11n and
802.11ac.2th ed. Cambridge: Cambridge University Press, 2013.
[2] R. Stacey. Proposed TGax Draft Specification. IEEE 802.11-16/0024r1,
March 2016.
[3] R. Stacey. TGax Editor´s Report. IEEE 802.11-17/1687/r1, Nov 2017.
[4] A. Chen et. al. 11ax LDPC Tone Mapper for 160MHz. IEEE 802.11-
15/1310r0, Nov 2015.
[5] R. P. F. Hoefel. "IEEE 802.11ax: Effects of IQ mismatching on the
performance of uplink multi-user MIMO,” in 21th IEEE International ITG
Workshop on Smart Antennas (WSA2017), Berlin, March 2017.
[6] R. P. F. Hoefel. “IEEE 802.11ax: Joint Effects of Power Control and IQ
Imbalance Mitigation Schemes on the Performance of OFDM Uplink Multi-
User MIMO”, in 2017 IEEE 86th Vehicular Technology Conference, Toronto,
Sept. 2017.
[7] F. Jiang, R. Porat and T. Mguyen. “On the impact of residual CFO in IL MU-
MIMO,” in 2016 IEEE International Conference on Acoustics, Speech and
Signal Processing (ICASSP), Shanghai, March 2016
[8] K. Oteri and R. Yang. Power Control for Multi-User Transmission in
802.11ax. IEEE 802.11-16/0331r1, March 2016.
[9] Z. Cai et. al. “Efficient encoding of IEEE 802.11n LDPC codes,” Electronics
Letters, vol. 42, no. 25, Dec. 2006.
[10] R. P. F. Hoefel. “IEEE 802.11ax: A study on techniques to mitigate the
frequency offset in the uplink multi-user MIMO”, in 8th 2016 IEEE Latin-
American Conference on Communication (LATINCOM 2016), Medellin,
Colombia, Nov. 2016.
[11] R. Stacey. Specification Framework for TGax. IEEE 11-15/0132r15, Jan.
2016.
[12] I. Held et. al. "Low complexity digital IQ imbalance correction in OFDM
WLAN receivers'', in IEEE 59st Vehicular Technology Conference (VTC'2004
Spring), Milan, 2004.
[13] E. Nash, “Correcting imperfections in IQ modulators to improve RF signal
fidelity,” in Analog Devices Application Note AN-1039.
[14] R. V. Nee. Uplink MU-MIMO sensitivity to power differences and
synchronization errors. IEEE 802.11-09/1036-00-00ac, Sept. 2009.
[15] R. Spitschka, Synchronization Algorithms for OFDM Systems Using the
Example of WLAN. Saarbrucken, Germany: VDM Verlag, 2008.
[16] N. Shah et. al. “Carrier frequency offset correction for uplink multi-user
MIMO for next generation Wi-Fi,” in 2015 International Conference on
Computing, Networking and Communications, Anaheim, USA, Fed. 2015.
[17] R. Porot et. al. 11ax Evaluation Methodology. IEEE 802.11-14/ 0571r12,
Jan. 2016.
[18] C. B Peel, B. M. Howhwald and A. L. Swindlehurst. "A vector -pertubation
technique for near-capacity multiantenna multiuser communication - Parte I:
channel inversion and regularization," IEEE Transaction on Communications,
vol. 53, no. 1, Fen. 2005, pp. 195-202.
[19] S. Veramani and A. V. Zelst, Interference cancellation for downlink MU-
MIMO. IEEE 802.11-09/1234r1, 2010.
164
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
