基于改进遗传算法的曲面拟合参数辨识.pdf

发布时间：2022-05-29 发布人：admin 分类：说明书资料大小：0.49M 资料格式：pdf 举报版权申诉

weixin_38622125-12155385-4744302543420776716.pdf-第1页.png

第1页 / 共8页

weixin_38622125-12155385-4744302543420776716.pdf-第2页.png

第2页 / 共8页

weixin_38622125-12155385-4744302543420776716.pdf-第3页.png

第3页 / 共8页

weixin_38622125-12155385-4744302543420776716.pdf-第4页.png

第4页 / 共8页

weixin_38622125-12155385-4744302543420776716.pdf-第5页.png

第5页 / 共8页

weixin_38622125-12155385-4744302543420776716.pdf-第6页.png

第6页 / 共8页

weixin_38622125-12155385-4744302543420776716.pdf-第7页.png

第7页 / 共8页

weixin_38622125-12155385-4744302543420776716.pdf-第8页.png

第8页 / 共8页

文本预览

基于改进遗传算法的曲面拟合参数辨识1 http://www.paper.edu.cn 谷川1, 潘国荣1,2，陈兴权1 ⒈同济大学测量与国土信息工程系，上海 (200092) ⒉现代工程测量国家测绘局重点实验室，上海 (200092) E-mail: guchuanhaha@163.com 摘要：空间曲面拟合是一个难以解决的复杂强非线性问题。已有的曲面拟合方法在求解明确的曲面表达式方面尚显难有作为。从参数辨识的角度来看，曲面拟合需要求解出坐标平移、旋转以及标准曲面方程参数。利用遗传算法在该领域的优势，并且针对经典简单遗传算法的缺陷进行了一系列改进。用MATLAB语言实现了改进算法的程序包。在钢结构马鞍面工业部件以及雷达天线椭圆抛物面表面检测两个工程实例中分别采用文章中的改进遗传算法和简单遗传算法进行了多次运算，并且对结果进行了比较。应用和比较结果表明，遗传算法能够较好地应用于空间曲面拟合，并且本文的改进算法更具优势。关键词：曲面拟合，参数辨识，遗传算法，改进，坐标转换，马鞍面(双曲抛物面)，椭圆抛物面中图分类号：TB22 文献标示码：A 1 引言在工业检测与逆向工程中，曲面拟合是一个经常涉及到的实际问题。由于实物的形状通常有严格的数学公式描述，通过对其表面点进行三维坐标采样，可以拟合出实物表面在空间坐标系中的几何方程，这对于发现实物的整体变形以及生成模型设计CAD图纸是至关重要的，在工业领域中有广泛的应用。目前已有的曲面拟合方法主要有基于插值和逼近的样条拟合[1] [2]，基于神经网络的曲面拟合[3]，格网法拟合[4]，这些方法在曲面拟合中具有一定的应用价值，但是，无法拟合出曲面方程的参数。比较基础的多项式曲面拟合由于精度较低不适用于高精度工业检测和逆向工程领域。文献[5]提出了一种出了按特征值、旋转角和平移量为参数拟合二次曲面的拟合方法，能够拟合出曲面方程的参数，但是算法比较复杂，需要大量的矩阵运算，并且通用性也不够好。正如文献[6]所阐述的，对于平面拟合问题，已经得到很好的解决，但对于复杂曲面，即便是简单的二次曲面的最小二乘拟合的研究也相对较少，而且已有的拟合算法存在方程求解困难、有奇异值和算法不稳定等问题，因此需要探索采用一种新的参数辨识方法。遗传算法(Genetic Algorithm，简称GA)是由美国Michigan大学的John H. Holland教授于 1975年在他的著作《Adaptation in Natural and Artificial Systems》中根据C. R. Darwin的生物进化论和G. Mendel的遗传变异理论提出的一种基于种群搜索的优化算法。其思想是随机产生初始种群, 通过选择(Reproduction)、交叉(Crossover) 和变异(Mutation) 等遗传算子的共同作用使种群不断进化, 最终得到最优解[7]。与其他优化方法相比， GA以单一字符串的形式描述所研究的问题，只需利用适应度函数进行优化计算，而不需要函数导数等其他信息，特别适合解决其他学科技术无法解决或难以解决的复杂和非线性问题,是继专家系统、人工神经网络之后又一受人青睐的人工智能学科，一直是研究的一个热点，被广泛地应用于组合优化、机器学习、自适应控制、规划设计、智能机器系统、智能制造系统、系统工程，人工智能、人工生命等领域，是21世纪智能计算 1本课题得到自动化工业测量系统的资助。 - 1 -

http://www.paper.edu.cn 中的关键技术之一[8]。习惯上将John H. Holland提出的遗传算法称为简单遗传算法（Simple Genetic Algorithm, 简称SGA）。和其它优化方法一样，由于全局性的要求，SGA作为一种通用的自适应随机搜索算法，还存在着早熟收敛(过早收敛于局部最优值)和收敛速度慢这两个缺陷，而且比较难克服,这给遗传算法的应用带来了很大的不便。为此，本文第2部分对SGA算法进行了改进，并且用MATLAB语言实现了改进之后的算法。 2 遗传算法的改进出现早熟往往是由于种群中出现了某些超级个体,随着模拟生物演化过程的进行,这些个体的基因物质很快占据种群的统治地位,导致种群中由于缺乏新鲜的基因物质而不能找到全局最优值；另一个主要原因是由于遗传算法中选择及杂交变异等算子的作用,使得一些优秀的基因片段过早丢失,从而限制了搜索范围,使得搜索只能在局部范围内找到最优值,而不能得到满意的全局最优值[9]。 Whitley认为，GA 中最重要的两个因素就是“种群多样性”和“选择压力”，而选择压力过大是导致早熟收敛的一个重要原因。过大的选择压力虽然可以加快算法的收敛速度，却会使种群中适应度不利于问题的求解的个体迅速“死亡”，种群的多样性遭到破坏，使得算法搜索空间减小，进而导致算法错误地收敛到局部最优值。降低选择压力虽然可以增大算法搜索到全局最优值的概率，但却会降低搜索效率，使算法的收敛速度变慢。为了使算法具有良好的性能，必须在提高选择压力和保持种群多样性之间达到某种平衡[10]。为提高遗传算法的搜索效率并保证得到问题的最优解，从以下几个方面提高遗传算法的效率及性能： 2.1 初始种群产生在 GA 中，采用实数编码策略比二进制编码策略具有精度高、搜索范围大、表达自然直观等优点。如此，能克服二进制编码所存在的诸多缺点，如不易求解高精度问题，不便于反应所求问题的特定知识及无法借鉴一些经典优化算法的宝贵经验等。 2.2 个体适应度计算计算适应度，需先构造适应度函数。合理的适应度函数能引导搜索朝最优化方向前行。本文的适应度函数是基于顺序的基础，其特点是个体被选择的概率与目标函数的具体值无关，仅于顺序有关。构造方法是先将种群中所有个体按目标函数值的好坏进行排序，设参数 β (0,∈ 1)，定义基于顺序的适应度函数为： ) 1( ββ −⋅ i=1,2,……,m (1) eval = i 1 − ( iX ' ) 式中， ' iX 为种群个体按优劣排序后的第 i 个个体。β 一般在 0.01~0.3 之间取值。 2.3 选择与交叉放弃赌轮选择，避免早期的高适应度个体迅速占据种群和后期的种群中因个体的适应大相差不大而导致种群停止进化。此处采用基于种群的按个体适应度大小排序的选择算法代替赌轮选择方法，其过程伪码描述如下： fitsort() - 2 -

http://www.paper.edu.cn { 将种群中的个体按适应度大小进行排序； } while(种群还没有扫描完) do { 排在最前面的个体复制两份；排在中间的个体复制一份；排在后面的个体不复制； } 在不破坏种群基因多样性的前提下加快算法的进化速度。交叉率按照公式（2）进行自适应调整： f f − − f f k 1 ⋅ ' f Pc = ≥ max max k 2 ' f < f ave ' ave ⎧ ⎪ ⎨ ⎪ ⎩ f ave (2) 式中，fmax 为群体中最大的适应度值；fave 为每代群体的平均适应度值；f’为要交叉的两个个体中较大的适应值。此处，只要设定 k1,k2（在[0，1]取值）的值，Pc 即可进行自适应调整。 2.4 个体子代的产生在选择出父本和母本后，按照交叉方法（单点、多点、一致交叉）进行 n 次交叉，产生 2n 个个体，再从这 2n 个个体中选出最优的两个个体加入到新的种群中。如此，既保留了父本和母本的基因，又在进化的过程中种群中个体的平均性能。 2.5 变异在 GA 中，如采用固定的变异概率 Pm，则当 Pm 取值很小时，变异算子对群体不会产生影响，不利于新的基因的引入；当 Pm 取值很大时，有可能破坏群体中的优良基因，使得算法收揽速度变慢甚至不收敛。此处，本文采用动态确定变异概率的方法，该方法既可防止优良基因因为变异而遭破坏，又可在陷入举步最优解时引入新的基因，该方法的伪码描述如下： if 个体的适应度>平均适应度 then Pm 取值很小或为 0； else Pm 取值相对很大 end if 如此，使得种群中好的基因不被破坏，既有利于不良基因的去除，又有利于新的基因的引入，从而可以很大程度的提高遗传算法的性能。具体的自适应调整的公式为： Pm = ⎧ ⎪ ⎨ ⎪⎩ k 3 ⋅ k 4 f f − max − max f f ave f ≥ f ave f < f ave (3) 式中，fmax 为群体中最大的适应度值；fave 为每代群体的平均适应度值；f’为要变异个体的适应度值。此处，只要设定 k3,k4（在[0，1]取值）的值，P 某即可进行自适应调整 - 3 -

http://www.paper.edu.cn 2.6 种群的进化将初始种群和产生的子代种群放在一起，形成新的种群，然后计算新的种群各个体的适应度，将适应度排在前面的 m 个个体保留，将适应度排在后面 m 个个体淘汰，这样种群便得到了进化。 2.7 进化终止条件每计划一次计算一下个个体的目标函数值，当相邻两次进化平均目标函数之差小于等于某一给定精度 ε 时，既满足如下条件 XF ( t )1( −+ XF ( t ) ε≤ (4) +tXF )1( ( 式中，平均目标函数值，此时，可终止进化。为第 t+1 次进化后种群的平均目标函数值， tXF ( ) 为第 t 次进化后种群的 2.8 遗传算法流程遗传算法流程的伪码表示如下： Procedure Genetic Algorithm; k=0; begin 初始化 P(k); 计算 P(k)的适应值； end while (不满足停止准则) do end begin 从 P(k-1)中选择 P(k);{复制算子} 重组 P(k)；{杂交和变异算子} 计算 P(k)的适应值； end k=k+1; 作者采用 MATLAB 编程语言，实现了本文提出的改进遗传算法的程序包 ImprovedGM。 3 曲面方程拟合参数辨识 3.1 曲面方程拟合的几何描述绝大多数情况下，检测仪器坐标系统与检测对象坐标系统不是统一的，事实上也是无法直接统一的，必须对检测点坐标进行坐标转换，使其统一到检测对象坐标系。最常用的坐标转换方法为七参数法，其转换公式如式(5)所示： − − − ( XX ( YY 0 ( ZZ (5) RRRr X Y 0 Z ⋅= + ⋅ ⋅ X Y Z ′ ′ ′ ⎤ ⎥ ⎥ ⎥ ⎦ ⎡ ⎢ ⎢ ⎢ ⎣ 0 ) ⎤ ⎥ ) ⎥ ) ⎥ ⎦ 0 ⎤ ⎥ ⎥ ⎥ ⎦ ⎡ ⎢ ⎢ ⎢ ⎣ ⎡ ⎢ ⎢ ⎢ ⎣ 0 0 ⋅ Z Y X 式中，(X, Y, Z)为转换前的坐标，(X’, Y’, Z’)为转换后的坐标，(X0, Y0, Z0)为平移参数，r 为尺度比例因子，RX，RY，RZ为旋转矩阵，其计算公式分别为： - 4 -

1 0 0 http://www.paper.edu.cn 。 ⎤ ⎥ ⎥ ⎥ ⎦ ⎡ ⎢ ⎢ ⎢ ⎣ 0 1 0 − ϕ Y XR = ， YR = ϕ X ϕ X 0 sin − cos cos ϕ Y 0 sin ϕ Y 0 cos ϕ X sin ϕ X ⎡ ⎢ ⎢ ⎢ ⎣ 由于工业检测一般所涉及到的范围比较小，故完全可认为比例因子r=1，如此，可在不影响拟合精度的基础上减少一个需要识别的参数。于是，需要辨识的参数有：3个旋转参数φX、 φY、φZ，三个平移参数X0，Y0，Z0，以及曲面标准方程参数，其个数由曲面标准方程本身决定。为了保证结果的唯一性和合理性，可以允许对曲面方程标准参数作一些合理的规定。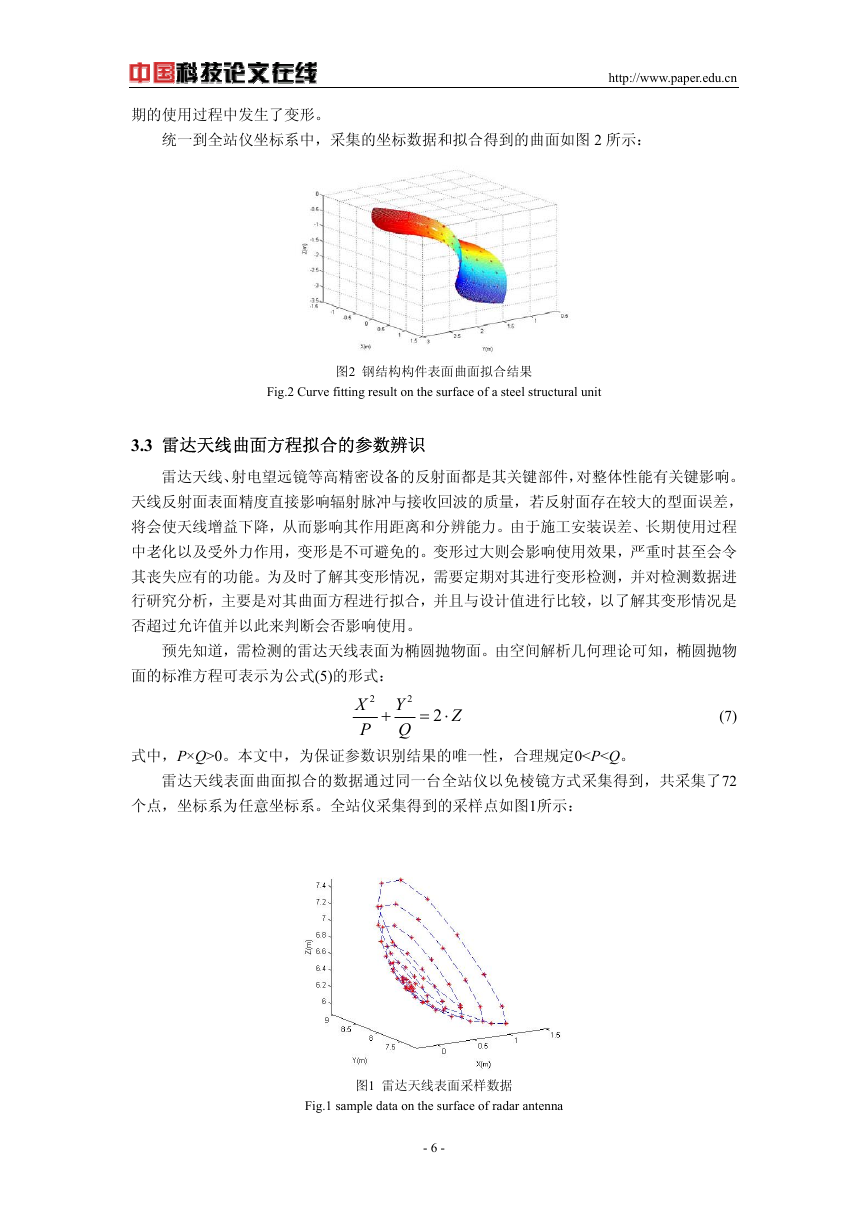 sin − ϕ Z cos ϕ Z 0 sin 0 cos ϕ Y cos ϕ Z sin ϕ Z 0 0 0 1 ⎤ ⎥ ⎥ ⎥ ⎦ ， ZR ⎤ ⎥ ⎥ ⎥ ⎦ = ⎡ ⎢ ⎢ ⎢ ⎣ 3.2 钢结构马鞍面工业构件曲面拟合宝钢某钢结构工业构件的表面为马鞍面（双曲抛物面），其表面曲面拟合的数据通过 Sokkia NET 1200全站仪以免棱镜方式采集得到，共采集了56个点，坐标系统为任意坐标系。全站仪标称精度指标为：测角精度1弧秒(0.5㎜/100m)，无棱镜测距精度为1㎜+2ppm。全站仪采集到的采样点数据如图1所示：图 1 钢结构构件表面采样数据 Fig.2 Sample data on the surface of a steel structural unit 由空间解析几何理论可知，马鞍面标准方程为： X 2 P − Y 2 Q = 2 Z (6) 式中，P×Q>0。为保证结果唯一性，合理规定0370s <120s 平均遗传代数平均计算时间有无陷入局部极小 >550 <200 SGA Improved GA 由于遗传算法的特性，每一次计算求得的参数值均在最后数位上略有差异，本文中采用改进遗传算法计算得到的参数值的平均值，分别为φX=- 1.06789814rad，φY= 0.1652586rad， φZ=- 0.08726693rad；X0= 1.95644m，Y0= 2.32768;m，Z0= 0.78972；P= 1.5253，Q= 1.7744。同设计的P0=1.5，Q0=1.8相比可知，P和Q都发生了一定的变化，分析认为该钢结构部件在长 >5㎜ <3㎜平均RMSE 有无 - 5 -

期的使用过程中发生了变形。统一到全站仪坐标系中，采集的坐标数据和拟合得到的曲面如图 2 所示： http://www.paper.edu.cn 图2 钢结构构件表面曲面拟合结果 Fig.2 Curve fitting result on the surface of a steel structural unit 3.3 雷达天线曲面方程拟合的参数辨识雷达天线、射电望远镜等高精密设备的反射面都是其关键部件，对整体性能有关键影响。天线反射面表面精度直接影响辐射脉冲与接收回波的质量，若反射面存在较大的型面误差，将会使天线增益下降，从而影响其作用距离和分辨能力。由于施工安装误差、长期使用过程中老化以及受外力作用，变形是不可避免的。变形过大则会影响使用效果，严重时甚至会令其丧失应有的功能。为及时了解其变形情况，需要定期对其进行变形检测，并对检测数据进行研究分析，主要是对其曲面方程进行拟合，并且与设计值进行比较，以了解其变形情况是否超过允许值并以此来判断会否影响使用。预先知道，需检测的雷达天线表面为椭圆抛物面。由空间解析几何理论可知，椭圆抛物面的标准方程可表示为公式(5)的形式： Y 2 Q X 2 P + 2 ⋅= Z (7) 式中，P×Q>0。本文中，为保证参数识别结果的唯一性，合理规定0

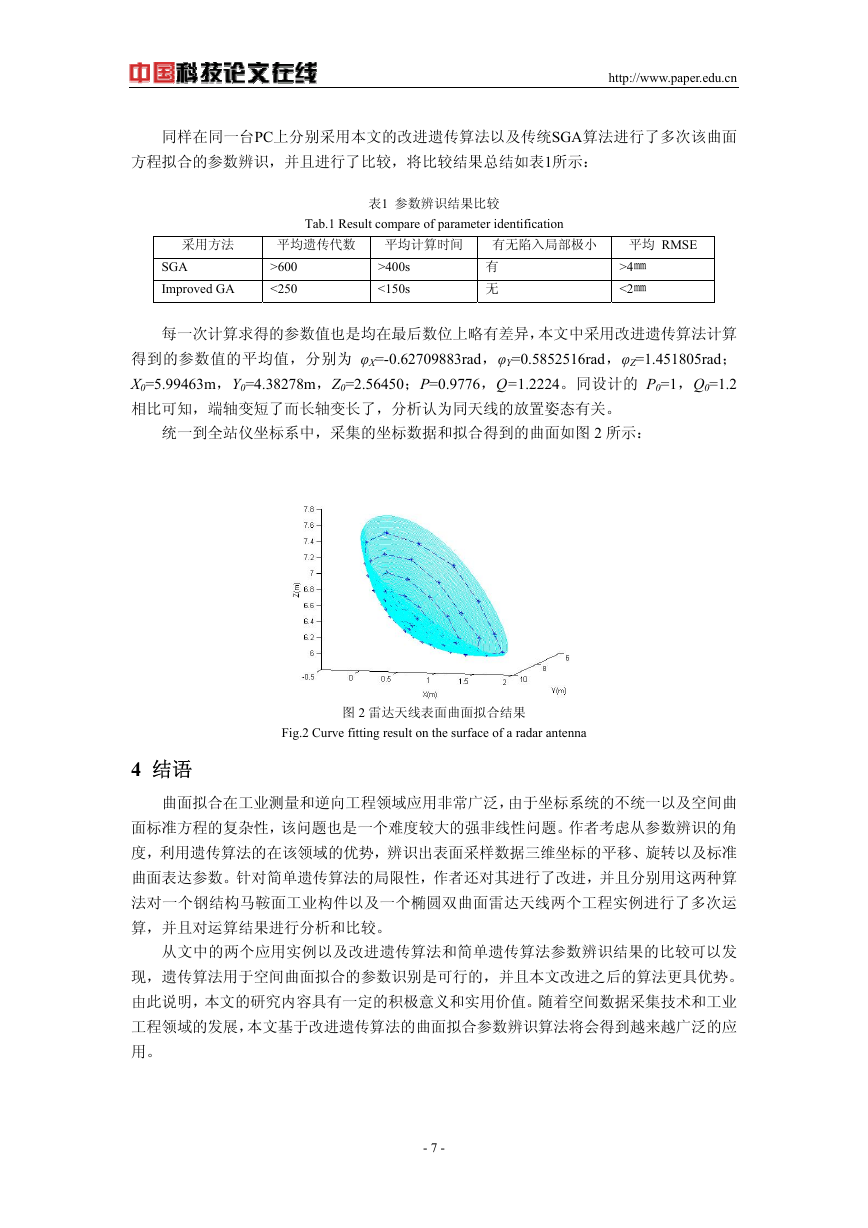
同样在同一台PC上分别采用本文的改进遗传算法以及传统SGA算法进行了多次该曲面方程拟合的参数辨识，并且进行了比较，将比较结果总结如表1所示： http://www.paper.edu.cn 表1 参数辨识结果比较 Tab.1 Result compare of parameter identification 有无平均 RMSE >4㎜ <2㎜采用方法 >400s <150s 平均遗传代数平均计算时间有无陷入局部极小 >600 <250 SGA Improved GA 每一次计算求得的参数值也是均在最后数位上略有差异，本文中采用改进遗传算法计算得到的参数值的平均值，分别为 φX=-0.62709883rad，φY=0.5852516rad，φZ=1.451805rad； X0=5.99463m，Y0=4.38278m，Z0=2.56450；P=0.9776，Q=1.2224。同设计的 P0=1，Q0=1.2 相比可知，端轴变短了而长轴变长了，分析认为同天线的放置姿态有关。统一到全站仪坐标系中，采集的坐标数据和拟合得到的曲面如图 2 所示：图 2 雷达天线表面曲面拟合结果 Fig.2 Curve fitting result on the surface of a radar antenna 4 结语曲面拟合在工业测量和逆向工程领域应用非常广泛，由于坐标系统的不统一以及空间曲面标准方程的复杂性，该问题也是一个难度较大的强非线性问题。作者考虑从参数辨识的角度，利用遗传算法的在该领域的优势，辨识出表面采样数据三维坐标的平移、旋转以及标准曲面表达参数。针对简单遗传算法的局限性，作者还对其进行了改进，并且分别用这两种算法对一个钢结构马鞍面工业构件以及一个椭圆双曲面雷达天线两个工程实例进行了多次运算，并且对运算结果进行分析和比较。从文中的两个应用实例以及改进遗传算法和简单遗传算法参数辨识结果的比较可以发现，遗传算法用于空间曲面拟合的参数识别是可行的，并且本文改进之后的算法更具优势。由此说明，本文的研究内容具有一定的积极意义和实用价值。随着空间数据采集技术和工业工程领域的发展，本文基于改进遗传算法的曲面拟合参数辨识算法将会得到越来越广泛的应用。 - 7 -

http://www.paper.edu.cn References [1] Wang W, Pottmann H, Liu Y. Fitting B-spline curves to point clouds by curvature-based squared distance minimization [J]. ACM Transactions on Graphics 2006, 25(2): 214-238. [2] Wang L Z,Zhu X X. Local interpolation blended B-spline surfaces and its conversion to NURBS surface [J]. Computer Aided Drafting, Design and Manufacturing, 1994, 4(2): 5-17. [3] 刘成龙, 杨天宇.基于BP神经网络的GPS高程拟合方法的探讨[J]. 西南交通大学学报, 2007, 42(02): 148-151. [3] Liu Chenglong, Yang Tianyu. Study on Method of GPS Height Fitting Based on BP Artificial Neural Network[J]. Journal of Southwest Jiaotong University 2007, 42(02): 148-151. [4] Wu Jian-Huang, Liu Wei-Jun, Wang Tian-Ran1, Zhao Ji-Bin. A Fitting Algorithm of Subdivision Surface from Noising and Dense Triangular Meshes[J]. Journal of Software, Vol.18, No.2, February 2007, 442-452. [5] 王解先. 工业测量中一种二次曲面的拟合方法[J]. 武汉大学学报（信息科学版）, 2007, 32(01) : 47-50. [5] Wang Jieian. A Method for Fitting of Conicoid in Industrial Measurement[J]. GEOMATICS AND INFORMATION SCIENCE OF WUHAN UNIVERSITY 2007, 32(01) : 47-50. [6] 顾步云, 周来水, 刘胜兰, 陈涛.逆向工程中二次曲面拟合方法的研究[J].南京:机械制造与研究, 2004 , 33 ( 1): 11-14. [6] GU Bu-yun, ZHOU Lai-shui, LIU Sheng-lan, CHEN Tao.Study on Algorithm of Quadric Surface Fitting in Reverse Engineering[J]. Machine Building & Automation, 2004 , 33 ( 1) : 11-14. [7] Holland J. Adaptation in Natural and Artificial Systems[M].University of Michgan Press,1975. [8] 王福林, 王吉权, 吴昌友, 吴秋峰.实数遗传算法的改进研究[J].鞍山: 生物数学学报, 2006, 21(1): 153-158. [8] WANG Fu-lin, WANG Ji-quan, WU Chang-you,WU Qiu-feng.The Improved Research on Actural Number Genetic Algorithms. Anshan: Journal of Biomathematics, 2006, 21(1): 153-158. [9] 黄绪明.一类改进的遗传算法.长沙: 长沙大学学报, 2005, 19(5): 1-4. [9] HUANG Xu-ming. A Kind of Improved Hereditary Algorithm[J]. Journal of Changsha University, 2005, 19(5), 1-4. [10] Whitley D. The Genetic algorithm and selection Pressure: why rank-based allocation reproduction trials is best[A].In Schaffer J, Proceeding of the 3rd international conference on genetic algorithm[C]. Los Altos: Morgan Kaufmann publishers, 1989. Parameter Identification of Surface Fitting Based on Improved Genetic Algorithm Gu Chuan1, Pan Guorong1,2, Chen Xingquan1 ⒈ Department of Surveying and Geo ⒉ Key Laboratory of Modern Engineering Surveying of SBSM, Shanghai (200092) -Informatics, Tongji University, Shanghai (200092) Abstract Spatial surface fitting is a complex highly nonlinear problem which is hard to solve. Existing surface fitting methods can barely figure out explicit curved surface expression. Viewing from the aspect of parameter identification, the parameters of coordinate translation, rotation and the standard curved surface equation are to be estimated. Genetic algorithm has particular advantages in this field. A series of modifications are made aiming at several defects of the classic simple genetic algorithm, and the improved algorithm is realized using MATLAB language. Both algorithms are used many times in double engineering examples, and the calculation results are compared. Applications and compares show that genetic algorithm can be well used in the field of spatial surface fitting, and the improved algorithm is better. Keywords: Surface fitting, parameter identification, genetic algorithm, improvement, coordinate transformation, hyperbolic paraboloid, elliptic paraboloid 作者简介：谷川（1983- ），男，山东省嘉祥县人，博士研究生，主要研究方向为精密工程测量、工业测量与测量数据处理。 - 8 -

分享到：

赞收藏

资料库

基于改进遗传算法的曲面拟合参数辨识.pdf

相关推荐

开发技术

热门标签

最新资料