logo资料库

智能PID算法在远程液位控制系统中的应用.doc

发布时间：2022-05-29 发布人：admin 分类：说明书 资料大小：0.18M 资料格式：doc 举报 版权申诉
第1页 / 共6页
第2页 / 共6页
第3页 / 共6页
第4页 / 共6页
第5页 / 共6页
第6页 / 共6页
资料共6页，全文预览结束
    智能PID算法在远程液位控制系统中的应用
    智能 PID 算法在远程液位控制系统中的应用 2008-10-10 11:15 来源： 互联网 1、引言 在工业过程控制系统中，目前采用最多的控制方式依然是 PID 控制。即使 在美国、日本等工业发达国家，PID 控制的使用率仍达 90%，可见 PID 控制在工业 过程控制中占有异常重要的地位。PID 控制技术经历了数十年的发展，从模拟 PID 控制发展到数字 PID 控制，技术不断完善与成熟。尤其近十多年来，随着微处理技 术的发展，国内外对智能控制的理论研究和应用研究十分活跃，智能控制技术发展 迅速，如专家控制、自适应控制、模糊控制等，现已成为工业过程控制的重要组成 部分。智能控制与常规 PID 控制相结合，形成所谓智能 PID 控制，这种新型的控制 方式已引起人们的普遍关注和极大兴趣，并已得到较为广泛的应用。本文介绍了一 种应用于远程液位控制的智能 PID 控制算法，它有不依赖于系统控制对象精确模型 的特点，有较好的鲁棒性。 2、控制对象及特征 某建材企业的生产用水以河水为水源，简单净化后经加压泵站输送到屋顶 水池，然后由屋顶水池经自然落差送往生产车间。加压泵采用变频控制。系统框图 如图 1 所示。 为保证水池的水位维持在设定的位置，使加压泵输送到水池的水量与车间 的用水量相一致，达到节电节水的目的，就必须根据用水量的变化及时调节加压泵 的转速（即出水量）。然而由于屋顶水池与加压泵站的距离较远，从加压泵站给水 量的增减到屋顶水池水位的变化，需经过长距离的输送管道，受管网压力、流量的 影响，系统惯性大，滞后时间长，用常规的 PID 控制方式系统产生振荡，水位大范 围波动不定。针对上述特征，采用可编程控制器实现的智能 PID 控制方案较好地解 决了这一问题。 3、常规的 PID 控制 通常闭环控制系统由控制器、执行部件、被控对象以及反馈检测元件几部
    分组成。原理框图如图 2 所示。 在闭环控制系统中，控制器是系统的核心，其控制算法决定了系统的控制 特性和控制效果。控制器最常用的控制规律是 PID 控制。PID 控制器是一种线性控 制器，它根据给定值 r（t）与实际输出值 c（t）构成控制偏差 e（t）（e（t）= r （t）-c（t）），将偏差 e（t）的比例（P）、积分（I）和微分（D）通过线性组 合构成控制量，对被控制对象进行控制，故称为 PID 控制器。 4、智能 PID 控制算法 4.1 典型的二阶系统分析 典型的二阶系统单位阶跃响应误差曲线如图 3 所示。在图 3 中Ⅰ、Ⅲ、Ⅴ、 Ⅶ……区域，误差朝绝对值减小的方向变化，此时可实施较弱的控制作用或保持等 待。在Ⅱ、Ⅳ、Ⅵ、Ⅷ……区域，误差朝绝对值增大的方向变化，此时可根据误差 的大小分别实施较强的或一般的控制作用。对于典型二阶系统阶跃响应过程分析如 下。 设 e（k）表示离散化的当前采样时刻的误差值，e（k-1）、e（k-2）分别 表示前一个和前二个采样时刻的误差值，则有： △e（k）=e（k）-e（k-1） △e（k-1）=e（k-1）-e（k-2） （4—1） （1）当|e（k）|≥emax 时，说明误差的绝对值很大，此时不论误差的变
    化趋势如何，都应考虑控制器按最大（或最小）输出，以迅速调整误差。即： u（k）=umax 当 e（k）>0 时 u（k）=umin 当 e（k）<0 时 （4—2） （2）当 e（k）·△e（k）>0 时，说明误差在朝绝对值增大的方向变化， 此时如果 emid≤|e（k）| u（k）=u（k-1）+ k1·△u（k） （4—3） 如果 emin≤|e（k）| u（k）=u（k-1）+△u（k） （4—4） （3）当 e（k）·△e（k）<0 时，说明误差在朝绝对值减小的方向变化， 此时如果 emid≤|e（k）| u（k）=u（k-1）+△u（k） （4—5） 如果 emin≤|e（k）| u（k）=u（k-1）+ k2·△u（k） （4—6） （4）当|e（k）| u（k）=u（k-1） （4—7） 以上式中： umax—控制器输出最大值; umin—控制器输出最小值; u（k-1）—第（k-1）次控制器输出; △u（k）—Kp[e（k）-e（k-1）]+Ki·e（k）+Kd[e（k）- 2e（k-1）+ e（k-2）]; k1—放大系数，k1>1; k2—抑制系数，0
    emax、emid、emin 为设定的误差界限，其中 emax>emid>emin。 4.2 智能 PID 控制规则 智能 PID 控制是在常规 PID 控制的基础上，根据专家及操作人员的实际经 验，针对具有大滞后、时变、非线性系统而提出的控制方法。其主要特点是按区段 进行不同算法的调节，它既有 bang-bang 控制的快速性，又有迟滞控制的稳定性和 抗干扰能力。根据上述的分析，总结出相应的控制规则如下： 规则 1：如果|e（k）|≥emax 则 u（k）=umax e（k）>0 时; 或 u（k）=umin e（k）<0 时 规则 2：如果 emid≤|e（k）| 则 u（k）=u（k-1）+ k1·△u（k） e（k）·△e（k）≥0 时; 或 u（k）=u（k-1）+△u（k） e（k）·△e（k）<0 时 规则 3：如果 emin≤|e（k）| 则 u（k）=u（k-1）+△u（k） e（k）·△e（k）≥0 时; 或 u（k）=u（k-1）+ k2·△u（k） e（k）·△e（k）<0 时 规则 4：如果|e（k-1）| 则 u（k）=u（k-1） 由上述四条规则可知，智能 PID 算法本质上是非线性的，能较好克服常规 PID 的缺点。规则 1、4 条体现了系统的快速性与稳定性，规则 2、3 条体现了 PID 变参数调节的自适应性。 5、采用 PLC 实现的智能控制策略
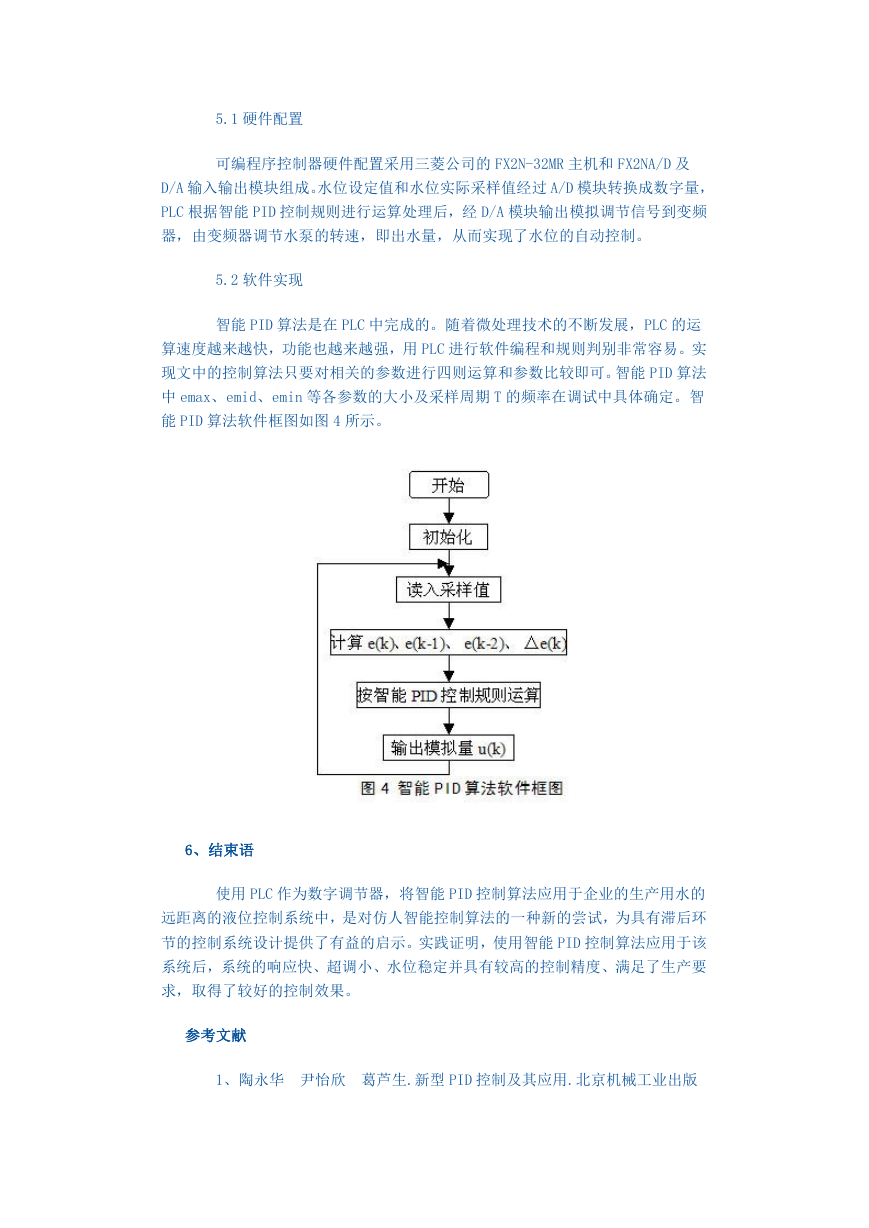
    5.1 硬件配置 可编程序控制器硬件配置采用三菱公司的 FX2N-32MR 主机和 FX2NA/D 及 D/A 输入输出模块组成。水位设定值和水位实际采样值经过 A/D 模块转换成数字量， PLC 根据智能 PID 控制规则进行运算处理后，经 D/A 模块输出模拟调节信号到变频 器，由变频器调节水泵的转速，即出水量，从而实现了水位的自动控制。 5.2 软件实现 智能 PID 算法是在 PLC 中完成的。随着微处理技术的不断发展，PLC 的运 算速度越来越快，功能也越来越强，用 PLC 进行软件编程和规则判别非常容易。实 现文中的控制算法只要对相关的参数进行四则运算和参数比较即可。智能 PID 算法 中 emax、emid、emin 等各参数的大小及采样周期 T 的频率在调试中具体确定。智 能 PID 算法软件框图如图 4 所示。 6、结束语 使用 PLC 作为数字调节器，将智能 PID 控制算法应用于企业的生产用水的 远距离的液位控制系统中，是对仿人智能控制算法的一种新的尝试，为具有滞后环 节的控制系统设计提供了有益的启示。实践证明，使用智能 PID 控制算法应用于该 系统后，系统的响应快、超调小、水位稳定并具有较高的控制精度、满足了生产要 求，取得了较好的控制效果。 参考文献 1、陶永华 尹怡欣 葛芦生.新型 PID 控制及其应用.北京机械工业出版
    社.1998.9 2、廖常初.可编程序控制器的编程方法与工程应用.重庆.重庆大学出版 社.2001.2 3、高金源.自动控制工程基础.北京.中央广播电视大学出版社.1992.2
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料