天牛须算法.pdf

发布时间：2022-06-20 发布人：admin 分类：说明书资料大小：0.47M 资料格式：pdf 举报版权申诉

c2fda446-49d9-4221-84b0-8c7641594b9e.pdf-第1页.png

第1页 / 共17页

c2fda446-49d9-4221-84b0-8c7641594b9e.pdf-第2页.png

第2页 / 共17页

c2fda446-49d9-4221-84b0-8c7641594b9e.pdf-第3页.png

第3页 / 共17页

c2fda446-49d9-4221-84b0-8c7641594b9e.pdf-第4页.png

第4页 / 共17页

c2fda446-49d9-4221-84b0-8c7641594b9e.pdf-第5页.png

第5页 / 共17页

c2fda446-49d9-4221-84b0-8c7641594b9e.pdf-第6页.png

第6页 / 共17页

c2fda446-49d9-4221-84b0-8c7641594b9e.pdf-第7页.png

第7页 / 共17页

c2fda446-49d9-4221-84b0-8c7641594b9e.pdf-第8页.png

第8页 / 共17页

文本预览

BAS: 天牛须搜索智能优化算法

基本情况  天牛须搜索(Beetle Antennae Search-BAS)，也叫甲壳虫须搜索，是2017年提出的一种高效的智能优化算法。  类似于遗传算法、粒子群算法、模拟退火等智能优化算法，天牛须搜索不需要知道函数的具体形式，不需要梯度信息，就可以实现高效寻优。  相比于粒子群算法，天牛须搜索只需要一个个体，即一只天牛，运算量大大降低。

仿生原理  天牛须搜索是受到天牛觅食原理启发而开发的算法。  天牛须搜索的生物原理：当天牛觅食时，天牛并不知道实物在哪里，而是根据食物气味的强弱来觅食。天牛有两只长触角，如果左边触角收到的气味强度比右边大，那下一步天牛就往左飞，否则就往右飞。依据这一简单原理天牛就可以有效找到食物。  天牛须搜索对我们的启发：食物的气味就相当于一个函数，这个函数在三维空间每个点值都不同，天牛两个须可以采集自身附近两点的气味值，天牛的目的是找到全局气味值最大的点。仿照天牛的行为，我们就可以高效的进行函数寻优。

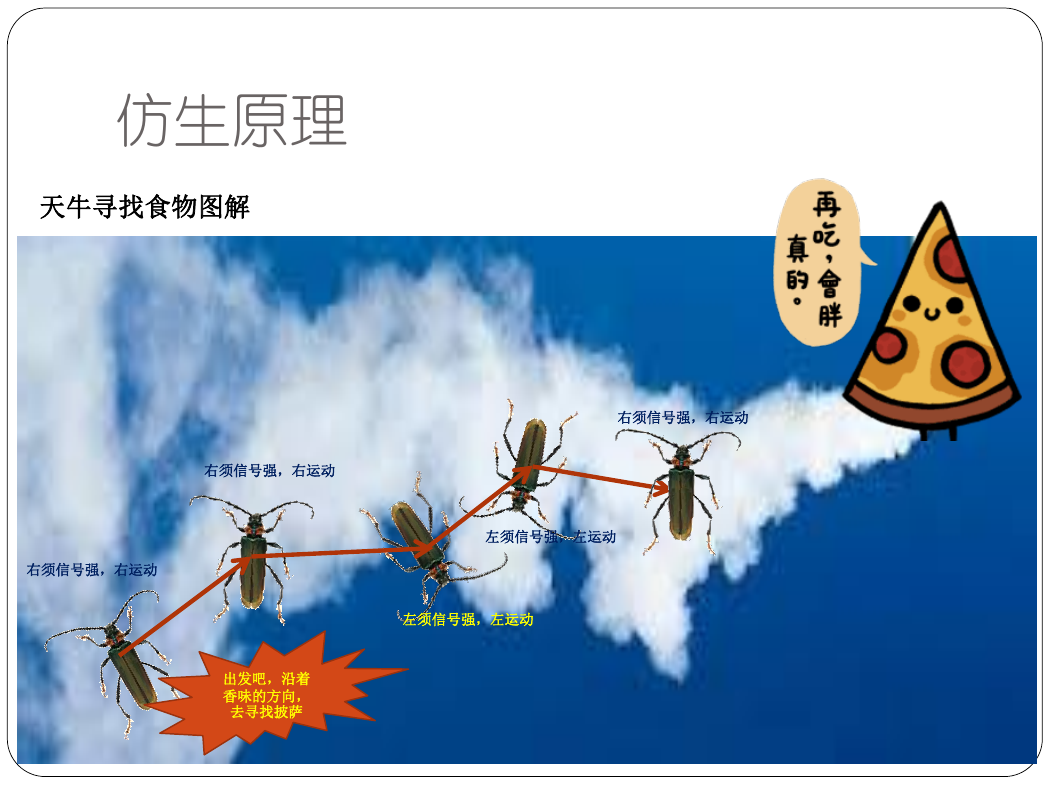
仿生原理天牛寻找食物图解右须信号强，右运动右须信号强，右运动右须信号强，右运动出发吧，沿着香味的方向，去寻找披萨左须信号强，左运动左须信号强，左运动

算法  天牛在三维空间运动，而天牛须搜索需要对任意维函数都有效才可以。因而，天牛须搜索是对天牛生物行为在任意维空间的推广。  我们采用如下的简化模型假设描述天牛：  1. 天牛左右两须位于质心两边。  2. 天牛步长step与两须之间距离d0的比是个固定常数即 step=c*d0其中c是常数。即，大天牛（两须距离长）走大步，小天牛走小步。天牛质心  3. 天牛飞到下一步后，头的朝向是随机的。天牛左须简化模型天牛右须两须之间的距离d0

建模（n维空间函数f最小化）  第一步：对于一个n维空间的优化问题，我们用xl表示左须坐标，xr表示右须坐标，x表示质心坐标，用 d0表示两须之间距离。根据假设3，天牛头朝向任意，因而从天牛右须指向左须的向量的朝向也是任意的，所以可以产生一个随机向量dir=rands(n,1)来表示它。对此归一化：dir=dir/norm(dir); 我们这样可以得到 xl-xr=d0*dir；显然， xl，xr还可以表示成质心的表达式：xl=x+d0*dir/2;xr=x-d0*dir/2. 天牛质心天牛左须天牛右须简化模型两须之间的距离d0

建模  第二步：对于待优化函数f，求取左右两须的值： fleft=f(xl); fright=f(xr); 判断两个值大小, 如果fleftfright,为了探寻f的最小值，则天牛向着右须方向行进距离step，即x=x-step*normal (xl-xr)； 如上两种情况可以采用符号函数sign统一写成： x=x-step*normal (xl-xr) *sign(fleft-fright)=x-step*dir *sign(fleft-fright). （注：其中normal是归一化函数）

建模基本步骤就这两步。总结下：  dir=rands(n,1); dir=dir/norm(dir); %须的方向  xl=x+d0*dir/2; xr=x-d0*dir/2. %须的坐标  fleft=f(xl); fright=f(xr); %须的气味强度  x=x-step*dir*sign(fleft-fright). %下一步位置循环迭代 几点说明： 1. 2. 实用中可以设置可变步长，由于假设2中我们认为step=c*d0其中c是常数，变核心代码如上，只有4行。步长意味着d0=step/c为变化的。

分享到：

赞收藏

资料库

天牛须算法.pdf

相关推荐

大数据

热门标签

最新资料