logo资料库

经验小波变换方面的论文.pdf

发布时间：2022-06-18 发布人：admin 分类：说明书 资料大小：2.45M 资料格式：pdf 举报 版权申诉
第1页 / 共15页
第2页 / 共15页
第3页 / 共15页
第4页 / 共15页
第5页 / 共15页
第6页 / 共15页
第7页 / 共15页
第8页 / 共15页
资料共15页，剩余部分请下载后查看
    See discussions, stats, and author profiles for this publication at: https://www.researchgate.net/publication/239523527 Empirical Wavelet Transform Article in IEEE Transactions on Signal Processing · August 2013 DOI: 10.1109/TSP.2013.2265222 READS 1,334 CITATIONS 184 1 author: Jerome Gilles San Diego State University 36 PUBLICATIONS 496 CITATIONS SEE PROFILE Some of the authors of this publication are also working on these related projects: Multicluster thresholding of unimodal histogram View project Imaging Through Atmospheric Turbulence View project All content following this page was uploaded by Jerome Gilles on 05 June 2014. The user has requested enhancement of the downloaded file.
    IEEE TRANS. ON SIGNAL PROCESSING, VOL. XX, NO. XX, FEBRUARY 2013 1 Empirical wavelet transform J´erˆome Gilles Abstract—Some recent methods, like the Empirical Mode De- composition (EMD), propose to decompose a signal accordingly to its contained information. Even though its adaptability seems useful for many applications, the main issue with this approach is its lack of theory. This paper presents a new approach to build adaptive wavelets. The main idea is to extract the different modes of a signal by designing an appropriate wavelet filter bank. This construction leads us to a new wavelet transform, called the empirical wavelet transform. Many experiments are presented showing the usefulness of this method compared to the classic EMD. Index Terms—Wavelet, Empirical mode decomposition, Adap- tive filtering I. INTRODUCTION A DAPTIVE methods to analyze a signal is of great in- terest to find sparse representations in the context of compressive sensing. “Rigid” methods, like the Fourier or wavelets transforms, correspond to the use of some basis (or frame) designed independently of the processed signal. The aim of adaptive methods is to construct such a basis directly based on the information contained in the signal. A well known way to build an adaptive representations is the basis pursuit approach which is used in the wavelet packets transform. Even though the wavelet packets have shown interesting results for practical applications, they still are based on a prescribed subdivision scheme. A completely different approach to build an adaptive representation is the algorithm called “Empirical Mode Decomposition” (EMD) proposed by Huang et al. [9]. The purpose of this method is to detect the principal “modes” which represent the signal (roughly speaking, a mode corresponds to a signal which have a compactly supported Fourier spectrum). This method has gained a lot of interest in signal analysis this last decade, mainly because it is able to separate stationary and non- stationary components from a signal. However, the main issue of the EMD approach is its lack of mathematical theory. Indeed, it is an algorithmic approach and, due to its non- linearity, is difficult to model. Nevertheless, some experiments [5]–[7] show that EMD behaves like an adaptive filter bank. Some recent works attempt to model EMD in a variational framework. In [4], the authors proposed to model a mode as an amplitude modulated-frequency modulated (AM-FM) Manuscript received October, 2012. Revised version received February, 2013. Copyright (c) 2012 IEEE. Personal use of this material is permitted. However, permission to use this material for any other purposes must be obtained from the IEEE by sending a request to pubs-permissions@ieee.org J. Gilles is with the Department of Mathematics, University of California, Los Angeles (UCLA), 520 Portola Plaza, Los Angeles, CA 90024, USA email: jegilles@math.ucla.edu. This work was partially founded by the following grants NSF DMS- 0914856, NSF DMS-1118971, ONR N00014-08-1-1119, ONR N0014-09-1- 0360, ONR MURI USC, the UC Lab Fees Research and the Keck Foundation. signal and then use the properties of such signals to build a functional to represent the whole signal. Then they are able to retrieve the different modes by minimizing this functional. Another proposed variational approach is the work of Hou et al. [8] where the authors also use the AM-FM formalism. They propose to minimize a functional which is build on some regularity assumptions about the different components and uses higher-order total variation priors. In this paper, we propose a new approach to build adaptive wavelets capable of extracting AM-FM components of a signal. The key idea is that such AM-FM components have a compact support Fourier spectrum. Separating the different modes is equivalent to segment the Fourier spectrum and to apply some filtering corresponding to each detected support. We will show that it is possible to adapt the wavelet formalism by considering distinct Fourier supports and then build a set of functions which form an orthonormal basis. Based on this construction, we propose an empirical wavelet transform (and its inverse) to analyze a signal. The remainder of the paper is organized as follows. Section II has two distinct subsections: in II-A, we recall the principle of the EMD algorithm and the AM-FM model; while in II-B, we recall some wavelet formalism which will be useful in our own construction and we discuss some of the existing adaptive wavelet methods. In section III, we build the proposed empirical wavelets and give some of their properties, then the empirical wavelet transform and its inverse are introduced. Section IV show many experiments based on simulated and real signals. The time-frequency representation based on the Hilbert transform is introduced in section V. In section VI, we address the question of the estimation of the number of modes. An extension to 2D signals (images) is presented in section VII. Finally, we conclude and give some perspectives in section VIII. II. EXISTING APPROACHES A. Empirical Mode Decomposition In 1998, Huang et al. [9] proposed an original method called Empirical Mode Decomposition (EMD) to decompose a signal into specific modes (we define the meaning of “mode” hereafter). Its particularity is that it does not use any prescribed function basis but it is self adapting accordingly to the analyzed signal f (t). In this paper, as we will use the Fourier formalism in section III, we adopt the description used in [4] which is slightly different from the original used in [9]. EMD aims to decompose a signal as a (finite) sum of N + 1 Intrinsic Mode Functions (IMF) fk(t) such that N k=0 f (t) = fk(t). (1)
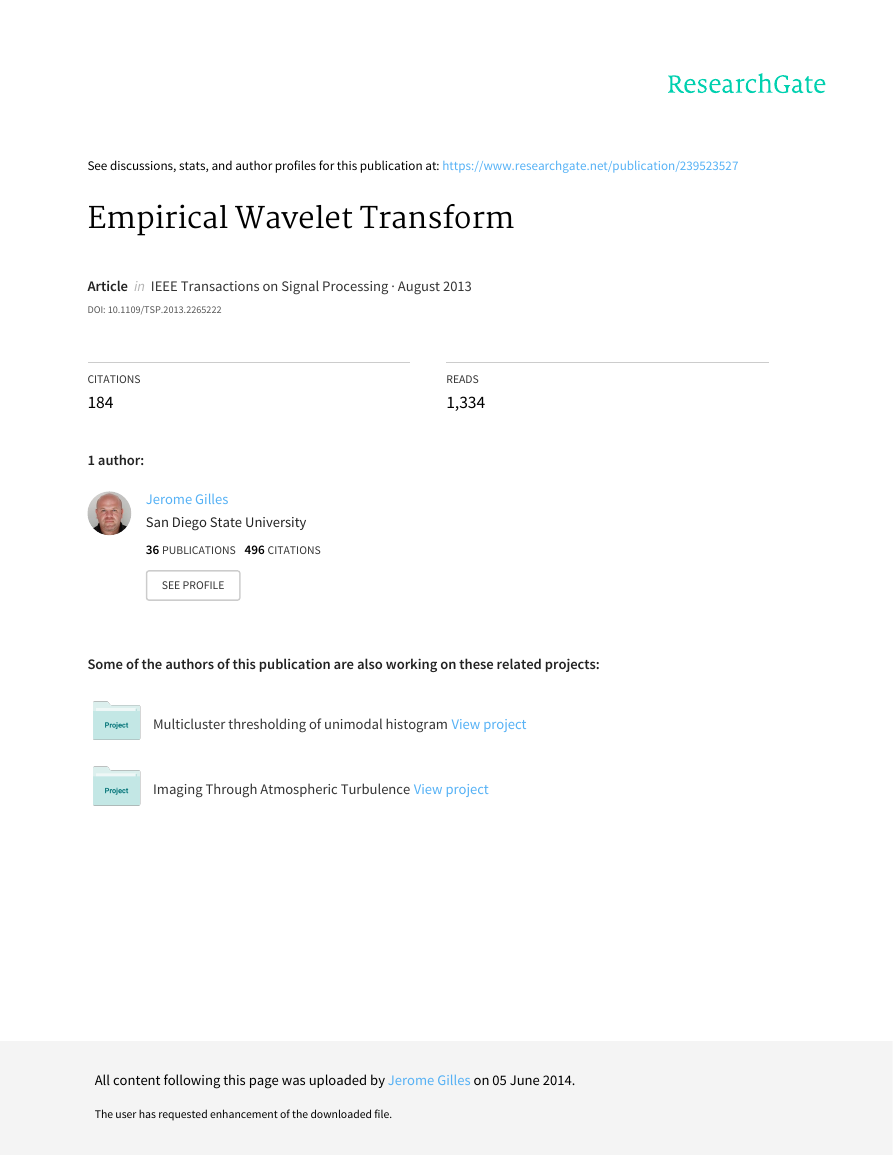
    2 IEEE TRANS. ON SIGNAL PROCESSING, VOL. XX, NO. XX, FEBRUARY 2013 Fig. 1. EMD: basic IMF detection. Envelopes detection on top (thin continuous: f, dashed: ¯f and f and thick continuous: m). On bottom: the first IMF candidate r1. An IMF is an amplitude modulated-frequency modulated function which can be written in the form where Fk(t), ϕ k(t) > 0 ∀t. fk(t) = Fk(t) cos (ϕk(t)) (2) The main assumption is that Fk and ϕ k vary much slower than ϕk. The IMF fk behaves as a harmonic component. Originally, the method of Huang et al. [9] to extract such IMFs is a pure algorithmic method. Candidates for an IMF are extracted by first computing the upper, ¯f (t), and lower, f (t), envelopes via a cubic spline interpolation from the maxima and minima of f. Then the mean envelope is obtained by computing m(t) = ( ¯f (t) + f (t))/2 and finally the candidate by r1(t) = f (t) − m(t) (see Fig. 1). Generally, r1(t) does not fulfill the properties of an IMF. A good candidate can be reached by iterating the same process to r1 and the subsequent rk. The final retained IMF is f1(t) = rn(t). Then the next IMF is obtained by the same algorithm applied on f (t)−f1(t). The remaining IMFs can be computed by repeating this algorithm on the successive residues. The interesting fact about this algorithm is that it is highly adaptable and is able to extract the non-stationary part of the original function. However, its main problem is that it is based on an ad-hoc process which is mathematically difficult to model. Consequently it is difficult to really understand what the EMD provides. For example, some problems appear when some noise is present in the signal. To deal with this problem, an Ensemble EMD (EEMD) was proposed in [17]. The authors propose to compute several EMD decompositions of the original signal corrupted by different artificial noises. Then the final EEMD is the average of each EMD. This approach seems to stabilize the obtained decomposition but it increases the computational cost. Another EMD approach is proposed in [8]. The authors Fig. 2. On top: dyadic wavelet tiling of the frequency line. On bottom: a wavelet packet like tiling. proposed to minimize a functional which looks for a sparse representation of f in a dictionary of IMFs. This variational method provides similar results as the original EMD algorithm. However, this functional is based on a scheme which uses higher order total variation terms, this makes the method sensitive to the presence of noise and some filtering must be added to the method. B. Wavelets approaches Nowadays, wavelet analysis is one of the most used tool in signal analysis. Let us fix some notations and recall the very basics about wavelet theory. For further details, we refer the reader to the extensive literature about the wavelet theory, see for example [3], [10], [12], [14]. The Fourier transform and its inverse are denoted ˆf and ˇf, respectively. In the temporal domain, a wavelet dictionary {ψu,s} is defined as the dilated, with a parameter s > 0, and translated by u ∈ R of a mother wavelet ψ (of zero-mean) as t − u ψu,s(t) = 1 √s ψ s . (3) Then the wavelet transform of f is obtained by computing the inner products Wf (u, s) = f, ψu,s. If s is a continuous variable then Wf (u, s) is called the continuous wavelet trans- form while if s = aj then Wf (u, s) = Wf (u, j) is called the discrete wavelet transform. A useful property of the wavelet transform is that it can be viewed as the application of a filter bank (each filter corresponds to one scale). In practice, the most used case is the dyadic case, s = 2j. It can be shown that such a case corresponds to tile the time-frequency plane like in top of Fig. 2. As we are interested in developing adaptive representations, we recall some existing tentatives of adaptive wavelets con- struction. As far as we know there are a very few attempts in the literature. Probably the most known method is the wavelet packets in a basis pursuit framework based on successive scale refinements of the expansion. It provides an adaptive time- frequency plane tiling like in bottom of Fig. 2. Even though the wavelet packets are useful in many applications, they use a constant prescribed ratio in the subdivision scheme, which 0.20.40.60.81.0-22460.20.40.60.81.0-1.0-0.50.51.0ωππ/2π/4π/8...ωππ2π4π83π4......
    GILLES: EMPIRICAL WAVELET TRANSFORM 3 Fig. 3. Partitioning of the Fourier axis limits their adaptability. Another approach, called the Malvar-Wilson wavelets [10], [13], tries to build an adaptive representation by segmenting the temporal signal itself in order to separate the time intervals containing different spectral information. While the original idea is interesting, it turns out that the temporal segmentation is a difficult task to perform efficiently. In [15], the authors propose a method, called the brushlets, which aims to build an adaptive filter bank directly in the Fourier domain. Basically, it uses the idea of the Malvar- Wilson wavelets but segments the Fourier spectrum of the signal, instead of the signal itself. Conceptually the ideas in this work are really interesting, however the proposed con- struction is quite complicated and is also based on prescribed subdivisions. The last work we want to mention is a recent work of Daubechies et al. [4] entitled “synchrosqueezed wavelets”. This approach combines a classic wavelet analysis and a real- location method of the time-frequency plane information. This algorithm permits to obtain a more accurate time-frequency representation and consecutively it is possible to extract spe- cific “modes” by choosing the appropriate information to keep. All the above methods use either a prescribed scale subdivision schemes or a smart utilization of the output of a classic wavelet analysis. As far as we know, no work exists which aims to build a full adaptive wavelet transform. The remaining of the paper will addresses such construction. III. EMPIRICAL WAVELETS A. Definition We propose a method to build a family of wavelets adapted to the processed signal. If we take the Fourier point of view, this construction is equivalent to building a set of bandpass filters. One way to reach the adaptability is to consider that the filters’ supports depend on where the information in the spectrum of the analyzed signal is located. Indeed, the IMF properties are equivalent to say that the spectrum of an IMF is of compact support and centered around a specific frequency (signal dependent). For clarity, we only consider real signals (their spectrum is symmetric with respect to the frequency ω = 0) but the following reasoning can be easily extended to complex signal by building different filters in the positive and negative frequencies, respectively. We also consider a normalized Fourier axis which have a 2π periodicity, in order to respect the Shannon criteria, and we restrict our discussion to ω ∈ [0, π]. Let us start by assuming that the Fourier support [0, π] is segmented into N contiguous segments (we will discuss later how we can obtain such partitioning). We denote ωn to be the limits between each segments (where ω0 = 0 and ωN = π), see Fig. 3. Each segment is denoted Λn = [ωn−1, ωn], then it n=1 Λn = [0, π]. Centered around each ωn, we define a transition phase (the gray hatched areas on Fig. 3) Tn of width 2τn. is easy to see that N The empirical wavelets are defined as bandpass filters on each Λn. To do so, we utilize the idea used in the construction of both Littlewood-Paley and Meyer’s wavelets [3]. Then ∀n >   1 0   1 0 1 0 ˆφn(ω) = and ˆψn(ω) = 0, we define the empirical scaling function and the empirical wavelets by expressions of equations (4) and (5), respectively. π 1 2 β 2τn if |ω| ≤ ωn − τn (|ω| − ωn + τn) if ωn − τn ≤ |ω| ≤ ωn + τn otherwise 1 cos 0 (4) π π 1 1 2τn cos 2 β sin 2 β if ωn + τn ≤ |ω| ≤ ωn+1 − τn+1 2τn+1 (|ω| − ωn+1 + τn+1) if ωn+1 − τn+1 ≤ |ω| ≤ ωn+1 + τn+1 (|ω| − ωn + τn) if ωn − τn ≤ |ω| ≤ ωn + τn otherwise. (5) The function β(x) is an arbitrary Ck([0, 1]) function such that and β(x) + β(1− x) = 1 ∀x ∈ [0, 1]. β(x) = (6) Many functions satisfy these properties, the most used in the literature [3] is if x ≤ 0 if x ≥ 1 0 1 β(x) = x4(35 − 84x + 70x2 − 20x3). (7) Concerning the choice of τn, several options are possible. The simplest is to choose τn proportional to ωn: τn = γωn where 0 < γ < 1. Consequently, ∀n > 0, Eq. (4) and (5) simplify to Eq. (8) and (9) ˆφn(ω) = and ˆψn(ω) = π 1 cos 2 β 2γωn if |ω| ≤ (1 − γ)ωn (|ω| − (1 − γ)ωn) if (1 − γ)ωn ≤ |ω| ≤ (1 + γ)ωn otherwise, (8) π π 1 if (1 + γ)ωn ≤ |ω| ≤ (1 − γ)ωn+1 cos 2 β 1 2γωn+1 (|ω| − (1 − γ)ωn+1) if (1 − γ)ωn+1 ≤ |ω| ≤ (1 + γ)ωn+1 sin 2 β 2γωn (|ω| − (1 − γ)ωn) if (1 − γ)ωn ≤ |ω| ≤ (1 + γ)ωn otherwise. (9) πω1ω2ω3ωnωn+1oo2τ12τ22τ32τn2τn+1τN1oo
    4 IEEE TRANS. ON SIGNAL PROCESSING, VOL. XX, NO. XX, FEBRUARY 2013 Fig. 4. On left: Fourier transform of the scaling function for νn = 1, γ = 0.5. On right: Fourier transform of the wavelet function for νn = 1, νn+1 = 2.5, γ = 0.2. An example of ˆφn for νn = 1, γ = 0.5 and ˆψn for νn = 1, νn+1 = 2.5, γ = 0.2 is given in Fig. 4. B. Segmentation of the Fourier spectrum How we segment the Fourier spectrum is important as it is the step which provides the adaptability with respect to the analyzed signal to our method. We aim to separate different portions of the spectrum which correspond to modes e.g centered around a specific frequency and of compact support. In this paper, we assume that the number of segment, N, is given (in section VI we propose a method to estimate the number of bands). This implies that we need a total of N + 1 boundaries, but 0 an π are always used in our definition and consequently we need to find N − 1 extra boundaries. To find such boundaries, we first detect the local maxima in the spectrum and sort them in decreasing order (0 and π are excluded). Let us assume that the algorithm found M maxima. Two cases can appear: • M ≥ N: the algorithm found enough maxima to define the wanted number of segments, then we keep only the first N − 1 maxima, • M < N: the signal has less modes than expected, then we keep all the detected maxima and reset N to the appropriate value. Now, equipped with this set of maxima plus 0 and π, we define the boundaries ωn of each segment as the center between two consecutive maxima. C. Frame The following proposition shows that, by properly choosing the parameter γ, we can obtain a tight frame. Proposition 1: If γ < minn then the set ωn+1−ωn , n=1} is a tight frame of L2(R). ωn+1+ωn Proof: We follow the idea behind the construction of {φ1(t),{ψn(t)}N Meyer’s wavelet. +∞ The set {φ1(t),{ψn(t)}N ˆφ1(ω + 2kπ) 2 Fig. 5. Periodicity of the filter bank Fig. 6. text for details) Example of a Fourier partitioning of an empirical filter bank (see where Λσ(n) is a copy of Λn but centered at 2π − νn instead νn. First, it is easy to see that for ω ∈ ∪ we have N n+1 Λn/N ˆφ1(ω − 2π) 2 ˆψn(ω) 2 ˆψn(ω − 2π) 2 N n=1 Λσ(n)/N 2 ˆφ1(ω) N n+1 Tσ(n) n+1 Tn (12) = 1. + + + n=1 Then, it remains to look at the transition areas. Because of properties of β, this result also holds in Tn if consecutive Tn do not overlap: τn + τn+1 < ωn+1 − ωn ⇔ γωn + γωn+1 < ωn+1 − ωn ⇔ γ < ωn+1 − ωn ωn+1 + ωn . (13) (14) (15) This condition must be true for all n which is equivalent to said that condition (15) must be true for the smallest Tn and finally we get the result if γ < minn . ωn+1−ωn Fig. 6 gives an empirical filter bank example based on the set ωn ∈ {0, 1.5, 2, 2.8, π} with γ = 0.05 (the theory tells us that γ < 0.057). ωn+1+ωn D. Empirical wavelet transform N n=1} is a tight frame if + ˆψn(ω + 2kπ) 2 = 1. (10) From the previous section, we know how to build a tight frame set of empirical wavelets. We can now define the E f (n, t), in the same Empirical Wavelet Transform (EWT), W way as for the classic wavelet transform. The detail coefficients are given by the inner products with the empirical wavelets: W E f (n, t) = f, ψn = = ˆf (ω) ˆψn(ω) ∨ f (τ )ψn(τ − t)dτ , (16) (17) k=−∞ Accordingly to the 2π periodicity (see Fig. 5), it is enough to focus on the interval [0, 2π]. Following the previous notations, we can write n=1 N N [0, 2π] = Λn ∪ n=1 n=1 Λσ(n), (11) and the approximation coefficients (we adopt the convention E f (0, t) to denote them) by the inner product with the scaling W -Π-Π2-101Π2Π0.20.40.60.81.0-Π-Π2-101Π2Π0.20.40.60.81.0ωNωN−1ω1ω2=π2π1ˆφ1(ω)ˆψ1(ω)ˆψN(ω)ˆψN(ω−2π)ˆψ1(ω−2π)ˆφ1(ω−2π)oooo-3-2-11230.20.40.60.81.0
    GILLES: EMPIRICAL WAVELET TRANSFORM 5 function: W E f (0, t) = f, φ1 = = ˆf (ω) ˆφ1(ω) ∨ , f (τ )φ1(τ − t)dτ (18) (19) where ˆψn(ω) and ˆφ1(ω) are defined by Eq. 9 and 8, respec- tively. The reconstruction is obtained by f (t) = W W E f (0, t) φ1(t) + E f (n, t) ψn(t) = E f (0, ω) ˆφ1(ω) + E f (n, ω) ˆψn(ω) ∨ (20) . (21) N N n=1 n=1 W W Following this formalism, the empirical mode fk, as defined in section II-A, is given by f0(t) = W fk(t) = W E f (0, t) φ1(t), E f (k, t) ψk(t). IV. EXPERIMENTS (22) (23) A. Test signals We propose to test the Empirical Wavelet Transform on four different signals: three are artificial signals taken from [8] and one real electrocardiogram signal. Their description is given hereafter. 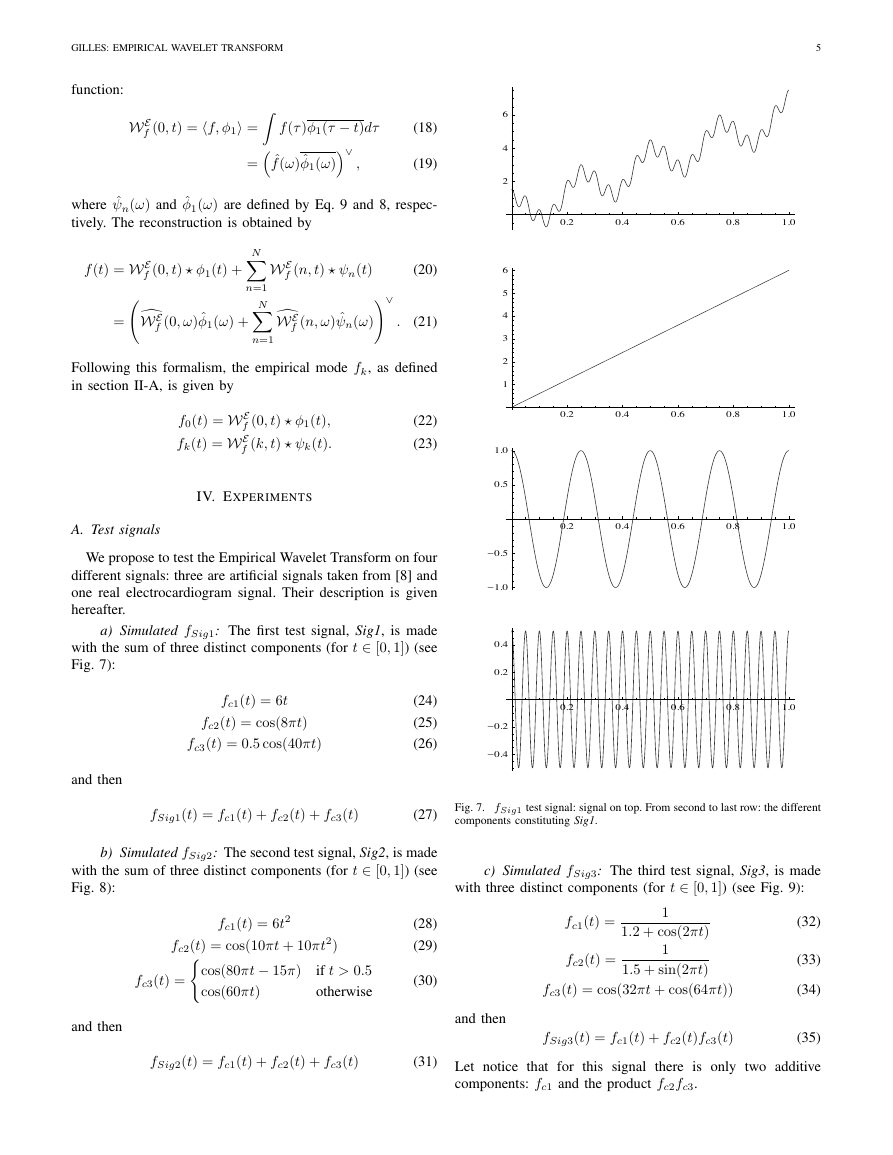a) Simulated fSig1: The first test signal, Sig1, is made with the sum of three distinct components (for t ∈ [0, 1]) (see Fig. 7): fc1(t) = 6t fc2(t) = cos(8πt) fc3(t) = 0.5 cos(40πt) (24) (25) (26) and then fSig1(t) = fc1(t) + fc2(t) + fc3(t) (27) Fig. 7. fSig1 test signal: signal on top. From second to last row: the different components constituting Sig1. 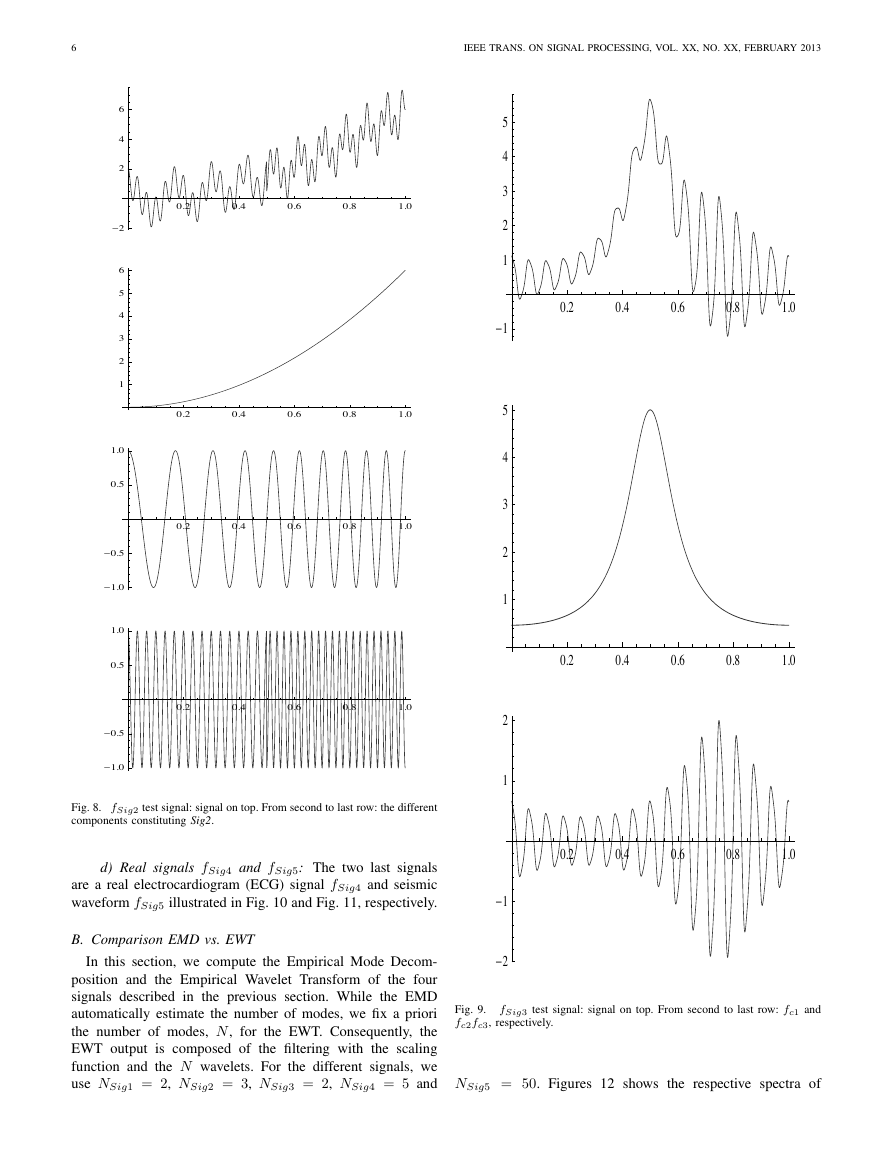b) Simulated fSig2: The second test signal, Sig2, is made with the sum of three distinct components (for t ∈ [0, 1]) (see Fig. 8): fc1(t) = 6t2 fc2(t) = cos(10πt + 10πt2) cos(80πt − 15π) cos(60πt) if t > 0.5 otherwise fc3(t) = and then fSig2(t) = fc1(t) + fc2(t) + fc3(t) (28) (29) (30) (31) c) Simulated fSig3: The third test signal, Sig3, is made with three distinct components (for t ∈ [0, 1]) (see Fig. 9): fc1(t) = fc2(t) = 1 1.2 + cos(2πt) 1 1.5 + sin(2πt) (32) (33) (34) (35) and then fc3(t) = cos(32πt + cos(64πt)) fSig3(t) = fc1(t) + fc2(t)fc3(t) Let notice that for this signal components: fc1 and the product fc2fc3. there is only two additive 0.20.40.60.81.02460.20.40.60.81.01234560.20.40.60.81.0-1.0-0.50.51.00.20.40.60.81.0-0.4-0.20.20.4
    6 IEEE TRANS. ON SIGNAL PROCESSING, VOL. XX, NO. XX, FEBRUARY 2013 Fig. 8. fSig2 test signal: signal on top. From second to last row: the different components constituting Sig2. d) Real signals fSig4 and fSig5: The two last signals are a real electrocardiogram (ECG) signal fSig4 and seismic waveform fSig5 illustrated in Fig. 10 and Fig. 11, respectively. B. Comparison EMD vs. EWT In this section, we compute the Empirical Mode Decom- position and the Empirical Wavelet Transform of the four signals described in the previous section. While the EMD automatically estimate the number of modes, we fix a priori the number of modes, N, for the EWT. Consequently, the EWT output is composed of the filtering with the scaling function and the N wavelets. For the different signals, we use NSig1 = 2, NSig2 = 3, NSig3 = 2, NSig4 = 5 and Fig. 9. fc2fc3, respectively. fSig3 test signal: signal on top. From second to last row: fc1 and NSig5 = 50. Figures 12 shows the respective spectra of 0.20.40.60.81.0-22460.20.40.60.81.01234560.20.40.60.81.0-1.0-0.50.51.00.20.40.60.81.0-1.0-0.50.51.00.20.40.60.81.0-1123450.20.40.60.81.0123450.20.40.60.81.0-2-112
    GILLES: EMPIRICAL WAVELET TRANSFORM 7 Fig. 10. fSig4: real ECG signal. Fig. 11. fSig5: real seismic waveform signal. Fig. 12. Detected Fourier supports for signals fSig1 to fSig4. each test signal and the detected boundaries for each filter support. We can observe that the algorithm is able is isolate the E different modes. The corresponding filtered signals W f (n, t) are presented in Fig. 13, 14, 15 and 17; while the EMD outputs are given in Fig. 18, 19, 20 and 21, respectively. We can observe that for the simulated test signals, the EMD always overestimates the number of modes and then sepa- rate some information which is originally part of the same component. Except for the high frequencies, it is difficult to interpret the EMD outputs compared with the known “true” components constituting the test signals. Concerning the results given by the EWT, we can see that it is able to detect the presence of modes in the spectrum and provides different components which are close to the original ones. However, in the case of fSig2, we can note that the algorithm separates the two last modes which were initially parts of the same component. In fact, this is not completely surprising as those modes have significant individual energy and can be considered as independent modes. About fSig3, another phenomenon appears. The initial part fc1 is decomposed as the sum of two modes (this sum is given in Fig. 16). If we look more closely, the detected boundaries, shown in Fig. 12, we can see that the scaling function is built upon a very small support while the next support contains the main information of fc1. If we ask the EWT to consider only N = 1 (as it supposed to be from the construction of fSig3), the first two supports shown in Fig. 12 are merged except that its boundary is moved closer to the zero frequency. This change in the boundary position has the consequence that some information of fc1 is now on the second support and then appear in the second mode instead the first one. In some sense, if we ask to use N = 1, we get a perturbed decomposition. This issue comes from the method we use to detect the boundaries of the Fourier support and suggests more investigations. Experiments on the real ECG signal seem to give the ad- vantage to the EWT because the EMD provides too many modes. Typically, the EMD modes six to nine are really difficult to interpret as such behavior is clearly not visible the EWT focuses on the in the signal itself. A contrary, Fig. 13. Modes extracted by the Empirical Wavelet Transform for fSig1. oscillating patterns we can observe in fSig4. Of course it will be very interesting to have the opinion of a cardiologist about the medical interpretation of such components. The different modes for the seismic signal are not provided here but we will present its time-frequency representation in section V as it more relevant for analysis purposes. V. TIME-FREQUENCY REPRESENTATION The time-frequency representation is useful to have the information of all components summarized in a single domain. In this paper, we follow the idea used in the Hilbert-Huang transform [9]. First, let us recall the definition of the Hilbert transform of a function f: +∞ −∞ f (τ ) t − τ Hf (t) = 1 π p.v. dτ (36) where the integral is defined by using the Cauchy principal value (p.v.) [11]. The Hilbert transform can be used to derive 1000200030004000-0.20.20.40.6200040006000800010000100050050010000.050.100.151000200030004000500060000.20.40.60.81000200030004000ˆfSig1ˆfSig20.050.100.150.200.250.30500100015002000250030000.020.040.060.080.100.120.1450100150200250ˆfSig3ˆfSig40.20.40.60.81.01234560.20.40.60.81.0-1.0-0.50.51.00.20.40.60.81.0-0.4-0.20.20.40.6
    分享到：
    赞 收藏

    相关推荐

    资料库

    信息化

    共收录1827份资料，累计6个分类，关注成员有19位，主要包括：管理软件,企业管理,电子商务,其它,IT管理,项目管理

    热门标签

    管理软件 企业管理 电子商务 其它 IT管理 项目管理

    最新资料