科技信息 ○IT 技术论坛○ SCIENCE & TECHNOLOGY INFORMATION 2008 年 第 26 期 CRC 纠错原理及其 Matlab 仿真 (西安外事学院信息工程学院 陕西 西安 710077) 魏西媛 蓝 洋 【摘 要】CR C(Cyclical R edundancy Checking)循环冗余校验码是一种重要的线性分组码, 通过多项式除法检测错误, 是在数据通信和数据 压缩中广泛应用的检错校验的循环码。 本文讨论了 CR C 的基本原理, 纠错检错方法及其算法分析, 最后以( 7, 3) 码为例对 CR C 实行 Matlab 仿真。 【关键词】CR C; Matlab 仿真 1.绪论 随着科学技术的进步, 人们对信息传递的要求逐渐提高。但在通 信系统中, 可靠性与有效性是对矛盾, 要求有效性提高, 必然使每个码 元所占的时间缩短, 从 而 受 干 扰 和 产 生 错 误 的 可 能 性 增 大, 可 靠 性 降 低了; 要提高信息的可靠性, 又使信息速率变慢有效性降低。因此, 合 理的解决有效性与可靠性这对矛盾, 是正确设计一个通信系统的关键 问题之一, 为保证 传 输 过 程 的 可 靠 性, 就 需 要 对 通 信 过 程 进 行 差 错 控 制。 循环冗余校验码 CRC(cyclic redundancy check)是一种高效率且可 靠的方法, 由线性 分 组 码 分 支 而 来 的, 是 一 种 通 过 多 项 式 除 法 检 测 错 误的很不寻常而又 巧 妙 的 方 法 , 一 方 面 它 有 很 强 的 检 测 能 力, 二 是 它 的编码器电路及错误检测器电路都很容易实现, 它的优点使它在通信 系统中得到了广泛的应用。 2.CRC 原理 循环冗余码 CRC 检验技术广泛应用于测控及通信领域。其基本 原理是: 在 K 位信息码后再拼接 R 位的校验码, 整 个 编 码 长 度 为 N 位, 因此, 这种编码又叫(n,k)码。对于一个给定的(n,k)码, 可以证明存在 一个最高次幂为 n- k=r 的多项式 G(x)。根据 G(x)可以生成 k 位信息的 校验码, 而 G(x)叫做这个 CRC 码的生成多项式。 校验码的生成过程为: 设信息多项式为 C(x), 将 C(x)左移 R 位, 则 可表示成 C(x)×2n, 这样 C(x)的右边就会空出 R 位, 这 就 是 校 验 码 的 位 置。通过 C(x)×2n 除以生成多项式 G(x)得到的余数就是校验码。 CRC 校 验 的 基 本 思 想: 利 用 线 性 编 码 理 论,在 发 送 端 根 据 要 传 送 的 k 位 二 进 制 码 序 列, 以 一 定 的 规 则 产 生 一 个 校 验 用 的 监 督 码 ( 既 CRC 码) r 位,并 附 在 信 息 后 边,构 成 一 个 新 的 二 进 制 码 序 列 数 共(k+r) 位,最后发送出去。在接收端,则根据信息码和 CRC 码之间所遵循的规 则进行检验,以确定传送中是否出错。 CRC 的计算过程: 1.设置 CRC 寄存器, 并给其赋值 FFFF(hex)。2. 将 数 据 的 第 一 个 8- bit 字 符 与 16 位 CRC 寄 存 器 的 低 8 位 进 行 异 或 , 并把结果存入 CRC 寄存器。3.CRC 寄存器向右移一位, MSB 补零, 移 出并检查 LSB。4.如果 LSB 为 0, 重复第三步; 若 LSB 为 1, CRC 寄存器 与多项式码相异或。5.重复第 3 与第 4 步直到 8 次移位全部完成。此 时一个 8- bit 数据处理完毕。6.重复第 2 至第 5 步直到所有数据全部 处理完成。7.最终 CRC 寄存器的内容即为 CRC 值。 3.差错检测和纠错 表 3.1 CRC 码的出错模式( G(x)=1011) 收到的 CRC 码 码位 A7 A6 A5 A4 A3 A2 A1 正确 错误 1 1 1 1 1 1 1 0 0 0 01 0 0 0 1 0 1 1 1 1 1 0 1 1 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 1 1 0 1 1 1 1 1 1 0 1 1 1 1 1 1 余数 出错 位 000 无 001 010 100 011 110 111 101 1 2 3 4 5 6 7 接 收 端 收 到 了 CRC 码 后 用 生 成 多 项 式 为 G(x)去 做 模 2 除 , 若 得 到余数为 0,则码字无误。如果有一位出错, 则余数不为 0, 而且不同位 出错, 其余数也不同。可以证明, 余数与出错位的对应关系只与码制及 生 成 多 项 式 有 关 , 而 与 信 息 位 无 关 。 表 3.1 给 出 了 G(x)=1011, C(c)= 1010 的出错模式, 改变 C(x)( 码字) , 只会改变表中码字内容, 不改变余 数与出错位的对应关系。 4.CRC 的算法分析 CRC 的算法很简单, 就是看能否在接收端检测出错误。除以 G(x) 余数是否为 0。 我们来看一个简单的讨论, 如 串 T=11010111010, 对应于 T(x)=x10+x9+x7+x5+x4+x3+x 串 E=00010110000, 对应于 E(x)=x7+x5+x4 串 T'=11000001010, 对应于 T'(x)=x10+x9+x3+x 加法是异或运算, 所以 E(x)和 T(x)中 的 x7 相 加 结 果 为 x7+x7=(1+1) ×x7=0。 所以我们必须得找出( T(x)+E(x)) /G(x)什么时候余数为 0? 既然( T (x)+E(x)) /G(x)=T(x) /G(x)+E(x) /G(x), 而 第 一 项 余 数 为 0, 则 后 一 项 决 定 余数, 所以问题可以是对于什么样的多项式 E(x), E(x) /G(x)余数为 0? 有如下说明: 漏检错误对应于 G(x)是 E(x)的因子的错误。那么在什么条件下, G (x)是 E(x)的因子? 首先我们考虑 T 中仅有一个比特位改变这种最简单的情况。此时 E(x)仅有 xk 一项, k 为整数, G(x)是 xk 的因子的唯一途径是: G(x)是 x 的 某次方, 所以, 只要 G(x)至少有两项, 这就不可能发生, 因此 CRC 就可 以检测出任何单位比特的错误。 其次考虑到一个长度 k≤r=G(x)的次数的突发错误, 假设 T(x)为 tntn- 1......tn+k- 1tn+k- 2……titi- 1……t1t0 tn+k- 1tn+k- 2……titi- 1 是被损坏的码字最前和最后的 比 特 位, 中 间 的 比 特位被随意地损坏, 也就是说。 E(x)=xi+k- 1+…+xi=xi×(xk- 1+…+1) 所以 E(x) G(x) = xi(xk- 1+…+1) G(x) 现在, 选择 G(x), 使 x 不是 G(x)的一 个 因 子, 因 此 G(x)和 前 面 部 分 的 xi 无关, 这样如果 G(x)是分子的因子, 那么它一定是(xk- 1+…+1)的因 子, 既 然 选 择 了 k≤r,那 么 k- 1≤r,G(x)不 可 能 是 一 个 更 低 此 方 多 项 式 的因子, 所以得出如下结论: 如果 x 不是 G(x)的因子, 那么长度小于等 于 G(x)次数的突发错误都可以检测出来。 再考虑影响奇数个比特位的任意长度的突发错误, 因为对每个损 坏的比特 E(x)都有对应项, 所 以 它 包 含 奇 数 个 项, 因 此 E(1)( 奇 数 个 1 的异或) 为 1。另外, 假设 x+1 是 G(x)的因子, 这样就可将 G(x)写成 G(x) =(x+1)×H(x), 此处 H(x)为某个表达式。 现 在 假 设 出 现 了 漏 检 错 误 , 即 意 味 着 G(x)是 E(x)的 一 个 因 子 , 将 G(x)用(x+1)×H(x)替 换 , 结 果 为 E(x)=(x+1)×H(x)×k(x), 若 令 x=1 计 算 该 方程, 则因子 x+1 使得 E(1)为 0, 这与前面 E(1)=1 矛盾。 很 明 显, 两 者 不 可 能 同 时 发 生, 如 果 坚 持 x+1 是 G(x)的 一 个 因 子 的假设, 那么漏检错误损坏的奇数个比特就不可能成立, 换句话说, 如 果 x+1 是 G(x)的一个因子, 那么所有损坏奇数个比特位的突发错误都 能检测出来。 最后一种情况是长度>G(x)的次数的突发错误, 由前所述。 E(x) G(x) = xi(xk- 1+…+1) G(x) 407 

科技信息 ○IT 技术论坛○ SCIENCE & TECHNOLOGY INFORMATION 2008 年 第 26 期 要介绍了 CRC 码的原理, 编译码问题。 但是, 这里 k- 1≥r=G(x)的次数, 所以 G(x)是(xk- 1+…+1)的一个因子 是可能的, 这种情况的机会有多大? 首先考虑 k- 1=r, 因为 G(x)的次数 也是 r, 所以 G(x)是(xk- 1+…+1)的一个因子意味着 G(x)=(xk- 1+…+1), 现在 xk- 1 和 1 之间的相对应的比特位确实损坏了, 既然有 r- 1 项, 损坏比特 位 的 可 能 组 合 就 有 2r- 1 种 , 若 假 设 所 有 组 合 以 相 同 几 率 出 现 , 那 么 组 合与 G(x)项精确匹配的几率为 1/2r- 1, 也就是说错误漏检率为 1- 2r- 1。 总的来说, 若 G(x)选择得当, CRC 是非常有效的。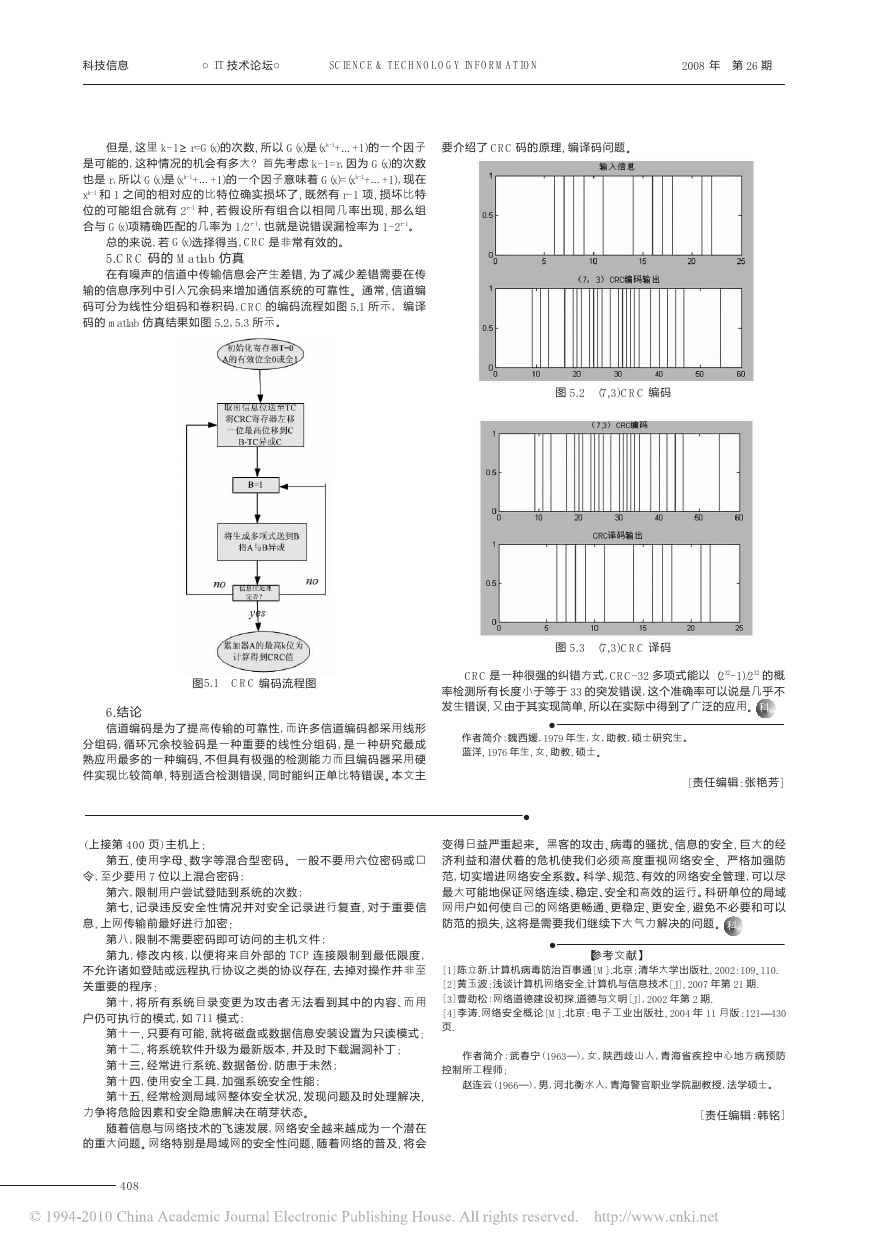 5.CRC 码的 Matlab 仿真 在有噪声的信道中传输信息会产生差错, 为了减少差错需要在传 输的信息序列中引入冗余码来增加通信系统的可靠性。通常, 信道编 码可分为线性分组码和卷积码, CRC 的编码流程如图 5.1 所示, 编译 码的 matlab 仿真结果如图 5.2, 5.3 所示。 图 5.2 (7,3)CRC 编码 图5.1 CRC 编码流程图 6.结论 信道编码是为了提高传输的可靠性, 而许多信道编码都采用线形 分组码, 循环冗余 校 验 码 是 一 种 重 要 的 线 性 分 组 码, 是 一 种 研 究 最 成 熟应用最多的一种编码, 不但具有极强的检测能力而且编码器采用硬 件实现比较简单, 特别适合检测错误, 同时能纠正单比特错误。本文主 ( 上接第 400 页) 主机上; 第五, 使 用 字 母 、数 字 等 混 合 型 密 码 。 一 般 不 要 用 六 位 密 码 或 口 令, 至少要用 7 位以上混合密码; 第六, 限制用户尝试登陆到系统的次数; 第七, 记 录 违 反 安 全 性 情 况 并 对 安 全 记 录 进 行 复 查, 对 于 重 要 信 息, 上网传输前最好进行加密; 第八, 限制不需要密码即可访问的主机文件; 第 九 , 修 改 内 核 , 以 便 将 来 自 外 部 的 TCP 连 接 限 制 到 最 低 限 度 , 不允许诸如登陆或远程执行协议之类的协议存在, 去掉对操作并非至 关重要的程序; 第十, 将 所 有 系 统 目 录 变 更 为 攻 击 者 无 法 看 到 其 中 的 内 容 、而 用 户仍可执行的模式, 如 711 模式; 第十一, 只要有可能, 就将磁盘或数据信息安装设置为只读模式; 第十二, 将系统软件升级为最新版本, 并及时下载漏洞补丁; 第十三, 经常进行系统、数据备份, 防患于未然; 第十四, 使用安全工具, 加强系统安全性能; 第十五, 经常检测局域网整体安全状况, 发现问题及时处理解决, 力争将危险因素和安全隐患解决在萌芽状态。 随着信息与网络技术的飞速发展, 网络安全越来越成为一个潜在 的重大问题。网络特别是局域网的安全性问题, 随着网络的普及, 将会 408 图 5.3 (7,3)CRC 译码 CRC 是一种很强的纠错方式, CRC- 32 多项式能以 (232- 1)/232 的概 率检测所有长度小于等于 33 的突发错误, 这个准确率可以说是几乎不 发生错误, 又由于其实现简单, 所以在实际中得到了广泛的应用。 科 ● 作者简介: 魏西媛, 1979 年生, 女, 助教, 硕士研究生。 蓝洋, 1976 年生, 女, 助教, 硕士。 [ 责任编辑: 张艳芳] ● 变得日益严重起来。黑客的攻击、病毒的骚扰、信息的安全, 巨大的经 济 利 益 和 潜 伏 着 的 危 机 使 我 们 必 须 高 度 重 视 网 络 安 全 、严 格 加 强 防 范, 切实增进网络安全系数。科学、规范、有效的网络安全管理, 可以尽 最大可能地保证网络连续、稳定、安全和高效的运行。科研单位的局域 网用户如何使自己的网络更畅通、更稳定、更安全, 避免不必要和可以 防范的损失, 这将是需要我们继续下大气力解决的问题。 科 ● 【参考文献】 [ 1] 陈立新.计算机病毒防治百事通[ M] .北京: 清华大学出版社, 2002: 109、110. [ 2] 黄玉波: 浅谈计算机网络安全.计算机与信息技术[ J] , 2007 年第 21 期. [ 3] 曹劲松: 网络道德建设初探.道德与文明[ J] , 2002 年第 2 期. [ 4] 李 涛.网 络 安 全 概 论[ M] .北 京: 电 子 工 业 出 版 社, 2004 年 11 月 版 : 121—430 页. 作 者 简 介: 武 春 宁( 1963—) , 女, 陕 西 歧 山 人, 青 海 省 疾 控 中 心 地 方 病 预 防 控制所工程师; 赵连云( 1966—) , 男, 河北衡水人, 青海警官职业学院副教授, 法学硕士。 [ 责任编辑: 韩铭]