高频注入算法IEEE论文.pdf

发布时间：2022-06-01 发布人：admin 分类：说明书资料大小：0.81M 资料格式：pdf 举报版权申诉

super318-10479232-4744300845244007087.pdf-第1页.png

第1页 / 共12页

super318-10479232-4744300845244007087.pdf-第2页.png

第2页 / 共12页

super318-10479232-4744300845244007087.pdf-第3页.png

第3页 / 共12页

super318-10479232-4744300845244007087.pdf-第4页.png

第4页 / 共12页

super318-10479232-4744300845244007087.pdf-第5页.png

第5页 / 共12页

super318-10479232-4744300845244007087.pdf-第6页.png

第6页 / 共12页

super318-10479232-4744300845244007087.pdf-第7页.png

第7页 / 共12页

super318-10479232-4744300845244007087.pdf-第8页.png

第8页 / 共12页

文本预览

IEEE TRANSACTIONS ON INDUSTRY APPLICATIONS, VOL. 44, NO. 3, MAY/JUNE 2008 777 A New Speed-Varying Ellipse Voltage Injection Method for Sensorless Drive of Permanent-Magnet Synchronous Motors With Pole Saliency—New PLL Method Using High-Frequency Current Component Multiplied Signal Shinji Shinnaka, Member, IEEE Abstract—This paper proposes a new sensorless vector control method for salient-pole permanent-magnet synchronous motors. With regard to phase estimation, the sensorless vector control method is featured by a new high-frequency voltage injection method (i.e., carrier modulation method), which is distinguished from the conventional ones by a unique ellipse shape of spatially rotating high-frequency voltage, and by a new phase-locked-loop method as a demodulation method whose input is a high-frequency current component multiplied signal. The new vector control method established by two innovative technologies for modulation/ demodulation can have the following high-performance and at- tractive characteristics. 1) It can allow 250% rated torque at standstill. 2) It can operate from zero to the rated speed under the rated motoring or regenerating load. 3) It accepts instant injection of the rated load even for zero-speed control. 4) Phase estimation is robust against inverter dead time, and proper phase estimate can be obtained even under circumstances where stator current crosses the zero at high frequency. 5) Computational load for estimating rotor phase is very small. Usefulness of the proposed new vector control method is veriﬁed through extensive experiments. Index Terms—Current component multiplied signal, high- frequency voltage injection, phase-locked loop (PLL), sensorless, synchronous motor. I. INTRODUCTION O NE OF THE most important challenges in sensorless vector control for permanent-magnet synchronous mo- tors (PMSMs) will be high-torque evolution based on proper phase (in other words, position) estimation of rotor at low speed including standstill. As a practical and, possibly, best solution to such problems, speciﬁcally for salient-pole PMSMs (SP-PMSMs), several constant-amplitude high-frequency volt- age injection methods have been proposed so far [1]–[8]. Paper IPCSD-07-100, presented at the 2007 IEEE International Electric Machines and Drives Conference, Antalya, Turkey, May 3–5, and approved for publication in the IEEE TRANSACTIONS ON INDUSTRY APPLICATIONS by the Industrial Drives Committee of the IEEE Industry Applications Society. Manuscript submitted for review May 7, 2007, and released for publication October 17, 2007. The author is with the Department of Electrical Engineering, Kanagawa University, Yokohama 221-8686, Japan (e-mail: shinnaka@kanagawa-u.ac.jp). Color versions of one or more of the ﬁgures in this paper are available online at http://ieeexplore.ieee.org. Digital Object Identiﬁer 10.1109/TIA.2008.921446 They inject constant-amplitude high-frequency voltage into SP-PMSMs in addition to fundamental driving voltage and estimate rotor phase by processing high-frequency current caused by the high-frequency voltage. Generally speaking, the methods have attractive advantage that rotor phase estimates are insensitive to motor parameters such as stator resistance and inductance, although the high-frequency current acts as disturbance from viewpoints of fundamental driving current control. The conventional constant-amplitude high-frequency voltage injection methods can be categorized into two classes such as constant-amplitude rotating type and constant-amplitude non- rotating type, according to the injected voltage shape in the ref- erence frame where the voltage is injected. The former injects constant-amplitude spatially rotating voltage, whose shape is sinusoidal in the injection reference frame [1]–[3]. On the other hand, the latter injects constant-amplitude nonrotating voltage, which does not spatially rotate in the injection reference frame and whose shape is sinusoidal or rectangular [4]–[8], [13]. As explained earlier, the constant-amplitude high-frequency voltage injection methods have been developed for high-torque evolution at low speed. However, recent applications of the high-frequency voltage injection methods to battery or hy- brid electric vehicles demand both high-torque evolution of 200%–250% rating at low speed including standstill and stable wide-range drive at least up to 100 rad/s (in other words, 10% of the maximum speed or 20% where feasible) [10]–[13]. If the demand is met, it is possible to make another sensorless method using fundamental components of the driving voltage and current to dedicate effectively to the higher speed drive, for example, 100–1500 rad/s, and consequently sensorless-driven vehicles become a reality [10]–[13]. The purpose of this paper is to propose a new sensorless vec- tor control method for SP-PMSMs taking a new high-frequency voltage injection approach, which is distinguished from the conventional ones by a unique ellipse shape of the spatially rotating high-frequency voltage, and by a new PLL-type phase detection method whose PLL input is a high-frequency current component multiplied signal. The minor axis of the ellipse shape varies dependently of rotor speed, and the injected voltage is no longer constant 0093-9994/$25.00 © 2008 IEEE

778 IEEE TRANSACTIONS ON INDUSTRY APPLICATIONS, VOL. 44, NO. 3, MAY/JUNE 2008 The electromagnetic characteristics of SP-PMSMs can be described as Fig. 1. Phase of rotor N-pole in γ−δ general reference frame, rotating at arbitrary angular speed ω. with amplitude. The resulting high-frequency current, from which the rotor phase is estimated, completely differs from that by the constant-amplitude rotating voltage injection method in [1]–[3] but is the same as “that at a standstill” by the constant-amplitude nonrotating voltage injection method in [4]–[8]. However, dif- ferent from that by the constant-amplitude nonrotating volt- age injection method [4]–[8], the shape of the high-frequency current remains the same over the entire speed range, i.e., the high-frequency current has an attractive property of speed independence. This property allows more stable rotor phase estimation that the constant-amplitude nonrotating voltage in- jection method could not attain. The new vector control method established by two innova- tive technologies can have the high-performance and attractive characteristics as follows. 1) It can allow 250% rated torque at standstill [2]–[8]. 2) It can operate from zero to the rated speed under the rated motoring or regenerating load [2]–[8]. 3) It accepts instant injection of the rated load even for zero- speed control. 4) Phase estimation is robust against the inverter dead time [1], [2], and proper phase estimate can be obtained even under circumstances where stator current crosses the zero at high frequency [15]. 5) Computational load for estimating rotor phase is very small, which would be the smallest among that of the methods with comparable performance [1]–[5]. This paper presents a new sensorless vector control method by focusing on two innovative technologies from their prin- ciples to design rules [9]. Usefulness of the proposed vector control method is veriﬁed through extensive experiments. Remark 1: In the following, the symbol “s” is used as a differential operator d/dt or as a Laplace operator. II. PHASE ESTIMATION PRINCIPLE A. Mathematical Model Consider the general reference frame where orthogonal γ−δ coordinates rotate at an arbitrary instant angular speed ω, as shown in Fig. 1. Rotating polarity is deﬁned such that the direction from principal axis (γ-axis) to secondary axis (δ-axis) is positive. Note that all of the following 2 × 1 vector signals related to SP-PMSMs are deﬁned in the general reference frame. ν1 = R1i1 + D(s, ω)φ1 φ1 = φi + φm φi = [LiI + LmQ(θγ)] i1 (1) (2) (3) (4) (5) Φ = const (6) Q(θγ) = D(s, ω) = sI + ωJ cos 2θγ sin 2θγ sin 2θγ − cos 2θγ cos θγ sin θγ φm = Φu(θγ) = Φ sθg = ω2n − ω , (7) where 2 × 1 vectors ν1, i1, and φ1 are the voltage, current, and ﬂux of stator, respectively; 2 × 1 vectors φi and φm are the components of stator ﬂux φ1—more precisely, φi indicates the ﬂux evolved directly by stator current i1, and φm is the ﬂux due to rotor magnet; I is a 2 × 2 identity matrix; J is a 2 × 2 skew symmetric matrix such as 0 −1 0 1 J = ω2n is the rotor electrical speed; R1 is the stator resistance; and Li and Lm are in- and mirror-phase inductances having a relation with d- and q-inductances such as Li Lm = 1 2 1 1 1 −1 Ld Lq . (9) Remark 2: Strictly speaking, the phase of the negative SP indicates that of the N- or S-poles. In this paper, it is assumed that the π-rad ambiguity regarding the phase has been solved by one of the well-known methods before initial motor driving [5], [7]. Then, the phase of the negative SP is treated as that of the N-pole. B. Phase Estimation Principle In the case of superinjection of a high-frequency voltage on fundamental driving voltage, the voltage, current, and ﬂux of stator can be described by two components of fundamental driving frequency (relatively low frequency) and high fre- quency such as   ν1 = ν1f + ν1h i1 = i1f + i1h φ1 = φ1f + φ1h (8) (10) where subscripts f and h indicate the associations of funda- mental driving frequency and high frequency, respectively. It is assumed that the frequency of the superinjected voltage is sufﬁciently high so that the following relation holds: R1i1h D(s, ω)φ1h . (11)

SHINNAKA: NEW SPEED-VARYING ELLIPSE VOLTAGE INJECTION METHOD FOR SENSORLESS DRIVE OF PMSMs 779 In the case where (10) holds, the following relation about the high-frequency components of stator signals ν1h, i1h, and φ1h can be obtained from (1)–(3) and (10): 2) The product of the ﬁrst and second components of (15) immediately yields the ﬁrst relation in (16). Applying the following relation ν1h = D(s, ω)φ1h φ1h = [LiI + LmQ(θγ)] i1h. (12) (13) For high-frequency stator signals ν1h, i1h, and φ1h in (12) and (13), the following useful theorem holds. Theorem 1 (Speed-Varying Ellipse Voltage Theorem): 1) If high-frequency voltage ν1h is selected to be a speed- varying signal such as ν1h = Vh cos ωht sin ωht ω ωh , Vh = const ωh = const (14) where Vh and ωh are constants and ω is the angular speed of the γ−δ coordinates (refer to Fig. 1), then the high- frequency current i1h as a response of the voltage turns out to be i1h = Vh ωhLdLq Li − Lm cos 2θγ −Lm sin 2θγ sin ωht. (15) 2) Let iγh and iδh be the γ- and δ-axis components of the high-frequency current i1h. The signal by multiplication of two components of the high-frequency current in (15) is reconstructed as a linear combination of a zero- frequency component ci1 having rotor phase information and a 2ωh high-frequency component ci2, namely iγhiδh = (2 sin2 ωht)ci1 = ci1 + ci2 (16) with Proof: −V 2 h Lm 2ω2 hL2 dL2 q ci1 = ci2 = − ci1 cos 2ωht. (Li − Lm cos 2θγ) sin 2θγ (17a) (17b) with 2 sin2 ωht = (1 − cos 2ωht) (20) to the ﬁrst relation yields the second relation in (16). Note that the high-frequency voltage in (14) tracks a tra- jectory of an ellipse shape. Although the major axis com- ponent of the ellipse is constant, the minor axis component varies proportionally to the speed ω of the γ−δ coordinates, which are expected to keep track of the d−q coordinates as will be explained later. Amplitudes of the major and minor axes are not the same in general; in addition, the minor axis component varies with the rotor speed. These facts mean that the high-frequency voltage in (14) has no longer constant amplitude. As a useful effect of the speed variance of the high-frequency voltage, the associated high-frequency current can be inde- pendent of the speed, i.e., the relation in (15) is valid for all rotor speeds and is independent of the rotor speed. The rotor phase is detected through processing the high-frequency cur- rent. Because the characteristics of the high-frequency current are speed independent, the rotor-phase overall speed range can be detected just like at a standstill. In other words, the high- frequency voltage injection method can be used stably in the higher speed range. The speed-independence characteristics of the high-frequency current play a key role in order that phase estimation methods using the high-frequency current can operate stably in wide speed range. As (15) clearly shows, the high-frequency current has infor- mation of the rotor phase θγ. The subsequent problem after the speed-independent high-frequency current is obtained is how to extract the phase information from the current. Consider the case where the γ−δ coordinates keep track of the d−q coordinates with a small rotor phase θγ. In that case, the zero- frequency (in other words, dc) component ci1 in (17a) can be approximated as ci1 ≈ Kθθγ Kθ = −V 2 ω2 hL2 h Lm dLq > 0. (21) (22) 1) Equations (12) and (13) can be solved with respect to the high-frequency current as −1 D [LiI−LmQ(θγ)] i1h = [LiI +LmQ(θγ)] = 1 LdLq −1(s, ω)ν 1h s2+ω2 D(s,−ω)ν1h. 1 Substituting (14) into (18) yields i1h = 1 LdLq [LiI − LmQ(θγ)] Vh ωh sin ωht 0 which leads to (15). (18) (19) The constant high-frequency ωh and amplitude Vh imply that Kθ deﬁned in (22) is a positive constant. Consequently, in the case, a simple linear relation holds between the rotor phase θγ evaluated in the γ−δ reference frame and the zero-frequency component ci1 of the high-frequency current component multi- plied signal (refer to the following Remark 3). The principle of the proposed phase estimation method is to estimate the rotor phase evaluated in the α−β (stator) reference frame using the component multiplied signal in (16), which is originally caused by injection of the high-frequency voltage in shape of speed-varying ellipse in (14) in the γ−δ coordinates

780 IEEE TRANSACTIONS ON INDUSTRY APPLICATIONS, VOL. 44, NO. 3, MAY/JUNE 2008 keeping track of the d−q coordinates. In more detail, the estimation principle is realized by the following three steps. 1) Inject the high-frequency voltage in shape of speed- varying ellipse in (14) in the γ−δ reference frame. 2) Detect the high-frequency current associated with the voltage and produce the signal through multiplication by two components of the current as in (16). 3) Estimate directly the rotor phase evaluated in the α−β (stator) reference frame using the component multiplied signal by exploiting the characteristics in (21) and (22). Remark 3: The rotor phase appears in the high-frequency current in the form in (15) that is the same as the one at “a standstill” in [4]–[8]. The form implies that, as long as one of the γ- and δ-components of the current is directly used for the phase estimation, at least a nonunity parameter originating from the motor parameters appears inevitably between the rotor phase and the directly used signal. This characteristic is com- mon to the phase estimations in the nonrotating high-frequency voltage injection method in [4]–[8] and is not unique to (21). In the aforementioned phase estimations, in which the FFT method in [4] and [5], the scalar heterodyne method in [6], the sign method in [7], and the high-frequency rotation method in [8] are included, the existence of the nonunity parameter should be taken into account. III. GENERALIZED INTEGRAL-TYPE PLL DRIVEN BY HIGH-FREQUENCY CURRENT COMPONENT MULTIPLIED SIGNAL A. Generalized Integral-Type PLL Method This section explains the aforementioned step 3) in detail. For sensorless vector controls of SP-PMSMs, the rotor phase θα evaluated in the α−β (stator) reference frame is necessary (refer to Fig. 1). In the situation that the γ−δ coordinates are in phase with the d−q coordinates, the phase ˆθα of γ-axis evaluated in the α−β reference frame can be a proper estimate of the rotor phase. Universal methods for such coordinate syn- chronization will be PLL methods typiﬁed by the generalized integral-type PLL method such as (23) ω = CPLL(s)uPLL ˆθα = 1 s ω with CPLL(s) = Cn(s) Cd(s) = cnmsm + cnm−1sm−1 + ··· + cn0 sm + cdm−1sm−1 + ··· + cd0 (24) where uPLL is an input signal to PLL, and cdi and cni are the constant parameters of the “PLL controller” CPLL(s) [1]. The original generalized integral-type PLL method assumes that the input signal uPLL is a proper estimate of the rotor phase θγ evaluated in the γ−δ reference frame and guarantees proper “phase-lock” ˆθα → θα under the assumption [1]. This paper newly proposes the direct use of the high-frequency Fig. 2. Phase synchronizer as a realization of the generalized integral-type PLL using input of the high-frequency current component multiplied signal. Fig. 3. Model for the PLL system. (a) Model A. (b) Model B. current component multiplied signal in (16) as the input uPLL as distinct from the PLL method in [1], i.e., uPLL = iγhiδh. (25) Generally speaking, the major computational load in the PLL process obtaining the ﬁnal phase estimate ˆθα evaluated in the stator reference frame is made up by the computation gaining a proper estimate of the rotor phase θγ [1]–[3]. The proposed PLL method does not require the computation and consequently succeeds in reducing the total computational load in the PLL process, particularly if compared with rotating-type constant- amplitude high-frequency voltage injection methods [1]–[3]. In the following, the PLL controller CPLL(s) that has the input in (25) is referred to as a “PLL controller designed to give good high-frequency rejection” or shortly “PLL controller with HF rejection.” Fig. 2 shows a realization of the generalized integral-type PLL with the PLL controller with HF rejection. B. Design of PLL Controller With HF Rejection It is necessary, for designing the PLL controller with HF rejection CPLL(s), to take the existence of high-frequency component of the signal in (25) into account; otherwise, the PLL system will lose function of the phase lock and will be unstable. This paper takes a strategy to suppress inﬂuences of the high-frequency component by the PLL system itself, keeping the phase-lock function. The PLL system based on (16), (17a), and (17b), (23)–(25) can be modeled as in Fig. 3(a). In the case where (21) holds, the PLL system can be modeled as in Fig. 3(b). This paper employs the following guideline for designing the PLL controller with HF rejection, according to the strategy.

SHINNAKA: NEW SPEED-VARYING ELLIPSE VOLTAGE INJECTION METHOD FOR SENSORLESS DRIVE OF PMSMs 781 Design Guidelines of PLL Controller With HF Rejection: 1) The mth-order polynomial Cd(s) has a factor of “s” in an 2) The (m + 1)th-order polynomial H(s) in (26) is the independent form. Hurwitz for every 0 < Kω ≤ 2 H(s) = sCd(s) + KωKθCn(s), 0 < Kω ≤ 2. (26) The purpose of guideline 1) is to prevent the high-frequency component contained in the input signal in (25) from appearing in coordinate speed ω at a constant speed drive. The purposes of guideline 2) are to treat the high-frequency component as an equivalent varying coefﬁcient 0 < Kω ≤ 2 of the PLL system [refer to Fig. 3(b)] and to design the PLL system to be stable. The following theorem gives concrete design rules for ﬁrst- and second-order PLL controller with HF rejections, based on the aforementioned guidelines. Theorem 2 (PLL Controller Theorem): 1) If Cd(s) is designed to be a ﬁrst-order polynomial such as CPLL(s) = cn1s + cn0 s , cn0 > 0 cn1 > 0 (27a) (27b) then polynomial H(s) results in the Hurwitz for every 0 < Kω ≤ 2. 2) If Cd(s) is designed to be a second-order polynomial such as CPLL(s) = cn1s + cn0 s(s + cd1) cn0 > 0, cn1 > 0, cd1 > 0 cd1 > cn0 cn1 (28a) (28b) then polynomial H(s) results in the Hurwitz for every 0 < Kω ≤ 2. Proof: 1) Consider a second-order polynomial A(s) such that A(s) = s2 + a1s + a0. (29) The polynomial A(s) is the Hurwitz if and only if all parameters ai’s are positive. From (27a), the condition cn0 = 0 is necessary for polynomial Cd(s) to have a factor of “s” in an indepen- dent form. In this case, H(s) deﬁned in (26) becomes a second-order polynomial such as The polynomial A(s) is the Hurwitz if and only if all parameters ai’s are positive and the following relation holds: a0 < a1a2. (32) From (28a), the condition cn0 = 0 is necessary for polynomial Cd(s) to have a factor of “s” in an indepen- dent form. In this case, H(s) deﬁned in (26) becomes a third-order polynomial such as H(s) = s3 + cd1s2 + KωKθ(cn1s + cn0). (33) According to the aforementioned general property, the condition that the third-order H(s) in (33) results in the Hurwitz for every 0 < Kω ≤ 2 is given by (28b). The high-frequency component ci2 deﬁned in (17b) contains the case of instant occurrence of equivalent coefﬁcient Kω = 0. As shown in Fig. 3(b), the instant occurrence of Kω = 0 means that the input to the PLL controller with HF rejection is zero. Because the PLL controller with HF rejection has the integral function according to the design guideline 1), interior and output signals of the PLL controller with HF rejection basically keep the values of just-before zero input, at instant of the zero input. This implies that the PLL controller with HF rejection shows the most desired response to the zero input and can keep stability. The PLL controller with HF rejection in (27a) and (27b) and (28a) and (28b) does not explicitly present conditions about equivalent coefﬁcient 0 < Kω ≤2 equivalently expressing effects of the high-frequency component, and as a matter of form, the PLL controllers in (27a) and (27b) and (28a) and (28b) accidentally appear similarly with the conventional ones using estimate of rotor phase θγ as input [1]. However, as shown in the proof, the PLL controllers in (27a) and (27b) and (28a) and (28b) take inﬂuences of the high-frequency component into account and are designed based on the strategy to suppress the inﬂuences of the high-frequency component by the PLL system itself. It is noteworthy that every conventional PLL controller cannot be necessarily used as a PLL controller with HF rejection. Remark 4: The PLL controller with HF rejection in (28a) can be treated as an integral (I) controller with a phase com- pensator or as a proportional and integral (PI) controller with a low-pass ﬁlter, i.e., · cn1 s = cn1 cd1 + cn0 cd1 s + cn0/cn1 s + cd1 1 s · cd1 s + cd1 . H(s) = s2 + KωKθ(cn1s + cn0). (30) CPLL(s) = According to the aforementioned general property, the condition that the second-order H(s) in (30) results in the Hurwitz for every 0 < Kω ≤ 2 is given by (27b). 2) Consider a third-order polynomial A(s) such that A(s) = s3 + a2s2 + a1s + a0. Note that these parameters cannot be designed independently, as shown in (28b) of Theorem 2. (31)

782 IEEE TRANSACTIONS ON INDUSTRY APPLICATIONS, VOL. 44, NO. 3, MAY/JUNE 2008 CHARACTERISTICS OF TEST MOTOR (SST4-20P4AEA-L) TABLE I C. Example of Design and Response This section shows a design example of the PLL controller with HF rejection and response examples of the PLL system installed with the controller. Example 1: Let the parameters of a test motor be those in Table I, and let the parameters of speed-varying high-frequency voltage in (14) be Vh = 23 ωh = 2π · 400 . (34) In this case, Kθ in (22) becomes Kθ = −V 2 ω2 hL2 h Lm dLq = 0.0352251 > 0. (35) Consider (27a) and (27b) as a PLL controller with HF rejection, and design the associated H(s) in (30) to have two stable zeros at s = −75 for the midvalue Kω = 1. In this case, two coefﬁcients of the PLL controller with HF rejection are deter- mined to be cn0 = 1.59687 · 105 > 0 cn1 = 4.25833 · 103 > 0 (36) which satisﬁes the parameter condition in (27b). Using the PLL controller with HF rejection CPLL(s) with parameters in (36), models A and B of the PLL system in Fig. 3 were constructed. 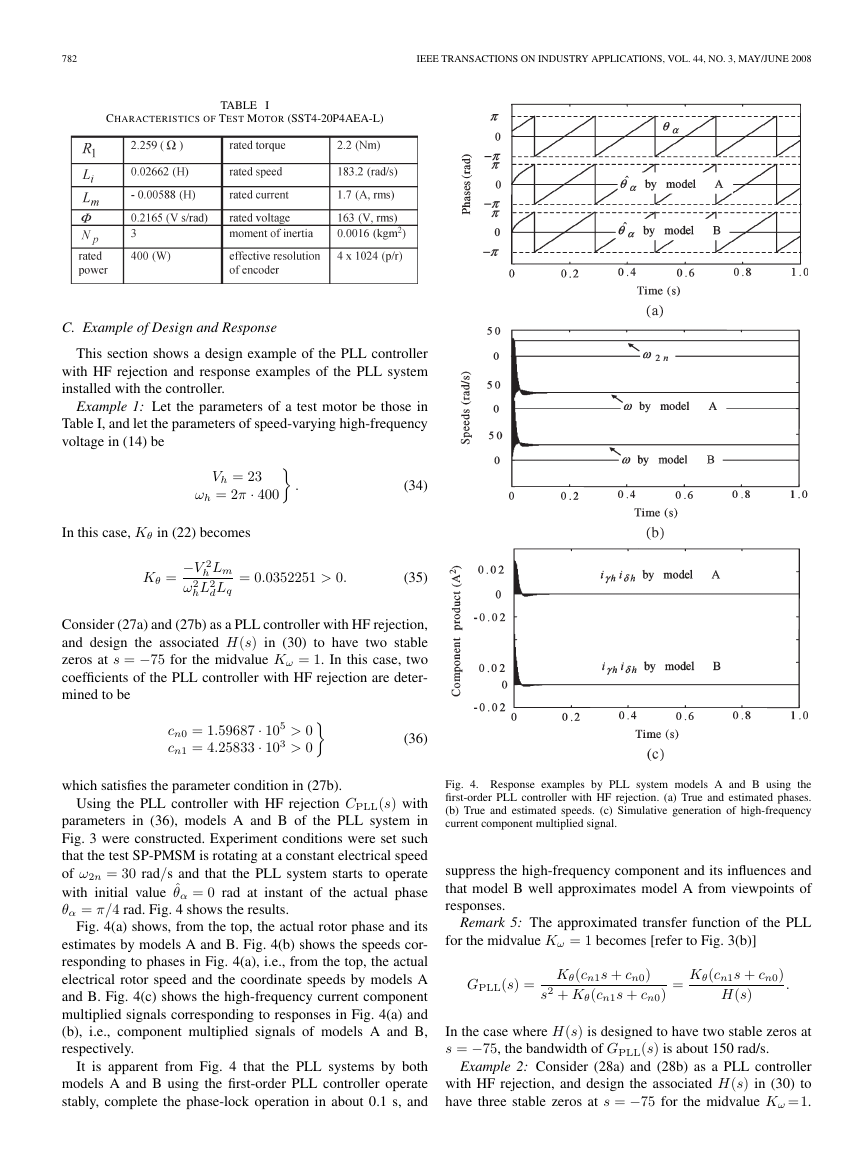Experiment conditions were set such that the test SP-PMSM is rotating at a constant electrical speed of ω2n = 30 rad/s and that the PLL system starts to operate with initial value ˆθα = 0 rad at instant of the actual phase θα = π/4 rad. Fig. 4 shows the results. Fig. 4(a) shows, from the top, the actual rotor phase and its estimates by models A and B. Fig. 4(b) shows the speeds cor- responding to phases in Fig. 4(a), i.e., from the top, the actual electrical rotor speed and the coordinate speeds by models A and B. Fig. 4(c) shows the high-frequency current component multiplied signals corresponding to responses in Fig. 4(a) and (b), i.e., component multiplied signals of models A and B, respectively. It is apparent from Fig. 4 that the PLL systems by both models A and B using the ﬁrst-order PLL controller operate stably, complete the phase-lock operation in about 0.1 s, and Fig. 4. Response examples by PLL system models A and B using the ﬁrst-order PLL controller with HF rejection. (a) True and estimated phases. (b) True and estimated speeds. (c) Simulative generation of high-frequency current component multiplied signal. suppress the high-frequency component and its inﬂuences and that model B well approximates model A from viewpoints of responses. Remark 5: The approximated transfer function of the PLL for the midvalue Kω = 1 becomes [refer to Fig. 3(b)] GPLL(s) = Kθ(cn1s + cn0) s2 + Kθ(cn1s + cn0) = Kθ(cn1s + cn0) H(s) . In the case where H(s) is designed to have two stable zeros at s = −75, the bandwidth of GPLL(s) is about 150 rad/s. Example 2: Consider (28a) and (28b) as a PLL controller with HF rejection, and design the associated H(s) in (30) to have three stable zeros at s = −75 for the midvalue Kω =1.

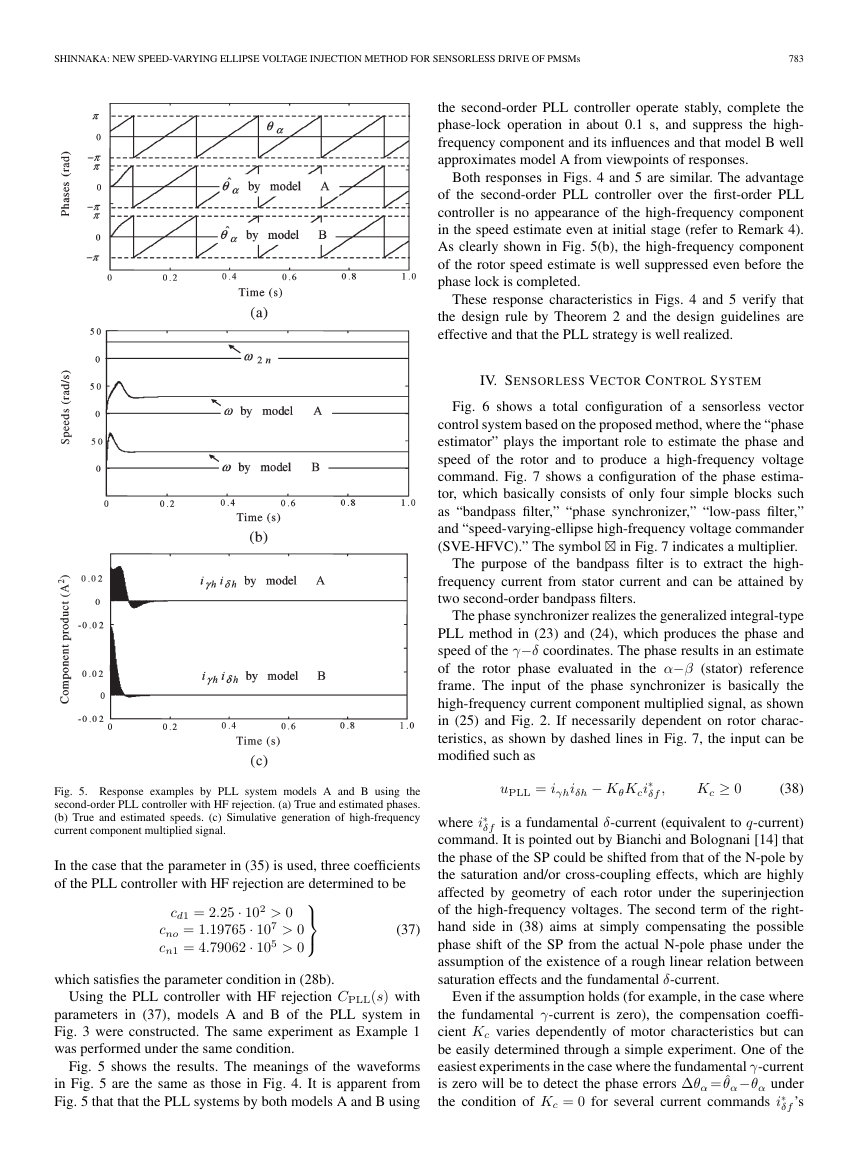
SHINNAKA: NEW SPEED-VARYING ELLIPSE VOLTAGE INJECTION METHOD FOR SENSORLESS DRIVE OF PMSMs 783 the second-order PLL controller operate stably, complete the phase-lock operation in about 0.1 s, and suppress the high- frequency component and its inﬂuences and that model B well approximates model A from viewpoints of responses. Both responses in Figs. 4 and 5 are similar. The advantage of the second-order PLL controller over the ﬁrst-order PLL controller is no appearance of the high-frequency component in the speed estimate even at initial stage (refer to Remark 4). As clearly shown in Fig. 5(b), the high-frequency component of the rotor speed estimate is well suppressed even before the phase lock is completed. These response characteristics in Figs. 4 and 5 verify that the design rule by Theorem 2 and the design guidelines are effective and that the PLL strategy is well realized. IV. SENSORLESS VECTOR CONTROL SYSTEM Fig. 6 shows a total conﬁguration of a sensorless vector control system based on the proposed method, where the “phase estimator” plays the important role to estimate the phase and speed of the rotor and to produce a high-frequency voltage command. Fig. 7 shows a conﬁguration of the phase estima- tor, which basically consists of only four simple blocks such as “bandpass ﬁlter,” “phase synchronizer,” “low-pass ﬁlter,” and “speed-varying-ellipse high-frequency voltage commander (SVE-HFVC).” The symbol in Fig. 7 indicates a multiplier. The purpose of the bandpass ﬁlter is to extract the high- frequency current from stator current and can be attained by two second-order bandpass ﬁlters. The phase synchronizer realizes the generalized integral-type PLL method in (23) and (24), which produces the phase and speed of the γ−δ coordinates. The phase results in an estimate of the rotor phase evaluated in the α−β (stator) reference frame. The input of the phase synchronizer is basically the high-frequency current component multiplied signal, as shown in (25) and Fig. 2. If necessarily dependent on rotor charac- teristics, as shown by dashed lines in Fig. 7, the input can be modiﬁed such as uPLL = iγhiδh − KθKci ∗ δf , Kc ≥ 0 (38) ∗ δf is a fundamental δ-current (equivalent to q-current) where i command. It is pointed out by Bianchi and Bolognani [14] that the phase of the SP could be shifted from that of the N-pole by the saturation and/or cross-coupling effects, which are highly affected by geometry of each rotor under the superinjection of the high-frequency voltages. The second term of the right- hand side in (38) aims at simply compensating the possible phase shift of the SP from the actual N-pole phase under the assumption of the existence of a rough linear relation between saturation effects and the fundamental δ-current. Even if the assumption holds (for example, in the case where the fundamental γ-current is zero), the compensation coefﬁ- cient Kc varies dependently of motor characteristics but can be easily determined through a simple experiment. One of the easiest experiments in the case where the fundamental γ-current is zero will be to detect the phase errors ∆θα = ˆθα−θα under ∗ the condition of Kc = 0 for several current commands i δf ’s Fig. 5. Response examples by PLL system models A and B using the second-order PLL controller with HF rejection. (a) True and estimated phases. (b) True and estimated speeds. (c) Simulative generation of high-frequency current component multiplied signal. In the case that the parameter in (35) is used, three coefﬁcients of the PLL controller with HF rejection are determined to be cd1 = 2.25 · 102 > 0 cno = 1.19765 · 107 > 0 cn1 = 4.79062 · 105 > 0   (37) which satisﬁes the parameter condition in (28b). Using the PLL controller with HF rejection CPLL(s) with parameters in (37), models A and B of the PLL system in Fig. 3 were constructed. The same experiment as Example 1 was performed under the same condition. Fig. 5 shows the results. The meanings of the waveforms in Fig. 5 are the same as those in Fig. 4. It is apparent from Fig. 5 that that the PLL systems by both models A and B using

784 IEEE TRANSACTIONS ON INDUSTRY APPLICATIONS, VOL. 44, NO. 3, MAY/JUNE 2008 Fig. 6. Conﬁguration of the proposed sensorless vector control. Fig. 7. Conﬁguration of the phase estimator. and to determine the constant Kc so as to minimize the values ∆θα−Kci ∗ df , for example, in the manner of the least squares. The purpose of the low-pass ﬁlter is to suppress the high- frequency component remaining in speed ω of the γ−δ coordi- nates and to produce an estimate of the electrical rotor speed. In the ideal case, the high-frequency component of the coordinate speed is completely eliminated, as shown in Fig. 4(b). However, in the actual cases, a small amount of the high-frequency component could remain in the coordinate speed. Generally, a ﬁrst-order low-pass ﬁlter is adequate for suppressing the remaining high-frequency component. The basic design rule for the cutoff frequency of the ﬁlter is that the cutoff should be much smaller than the frequency of the injected high-frequency voltage and be larger than the bandwidth of the speed control loop in the case of the speed control. Generally speaking, there is a wide freedom for the cutoff design. The purpose of the SVE-HFVC is to produce a high- frequency voltage command to be superimposed on the fundamental driving voltage command. The SVE-HFVC is realized based on (14) of Theorem 1 as , ∗ 1h = Vh ν cos ωt h ˆω2n ωh sin ωt h Vh = const ωh = const . (39) From practical viewpoints, the electrical speed estimate ˆω2n is used instead of the coordinate rotor speed ω, as clearly shown in (39). Fig. 8. Test system setup. Note that all functions of the phase estimator can be realized by means of software on a single digital signal processor (DSP) or microprocessor with no additional dedicated hardware. The basic computational load for realizing the phase estimator is almost equivalent to those for realizing two second-order bandpass ﬁlters, a PI-PLL, and a ﬁrst-order low-pass ﬁlter. It is apparent that the computational load for realizing the phase estimator is very small. As shown in Fig. 6, a mechanical speed estimate, which is used for speed control, is obtained through a simple division process of the electrical speed by the number of pole pairs Np. A ﬁlter Fbs(s) right after the vector rotator RT (·) is a band-stop ﬁlter to prevent the high-frequency component of stator current from entering into the current controller. In the case where high- frequency ωh locates the outside of bandwidth of the current control loop, the band-stop ﬁlter can be eliminated. V. EXPERIMENTS A. Conﬁguration of Experiment System In order to examine the basic performance of the proposed vector control method, extensive experiments were carried out by using the equipment shown in Fig. 8. The test motor is a 400-W SP-PMSM (IPMSM, SST4-20P4AEA-L) made by Yaskawa Electric Corporation (refer to Table I for the charac- teristics). A rotor-mounted encoder is just for monitoring of the actual rotor phase and speed and is not used for control. The load machine is a 3.7-kW dc motor (DK2114V-A02A-D01) of moment of inertia J = 0.085 kg · m2 and rated speed of 183 rad/s made by Toyo Denki Seizo K.K. The torque sensor system (TP-5KMCB, DPM-713B) is made by Kyowa Electric Instruments Company, Ltd.

分享到：

赞收藏

资料库

高频注入算法IEEE论文.pdf

相关推荐

行业

热门标签

最新资料