第1页 / 共33页
第2页 / 共33页
第3页 / 共33页
第4页 / 共33页
第5页 / 共33页
第6页 / 共33页
第7页 / 共33页
第8页 / 共33页
matlab 潮流计算程序.doc
一、问题重述
1.1 课程设计要求
1、在读懂程序的基础上画出潮流计算基本流程图
2、通过输入数据，进行潮流计算输出结果
3、对不同的负荷变化，分析潮流分布，写出分析说明。
4、对不同的负荷变化，进行潮流的调节控制，并说明调节控制的方法，并
列表表示调节控制的参数变化。
5、打印利用 DDRTS 进行潮流分析绘制的系统图，以及潮流分布图。
1.2 课程设计题目
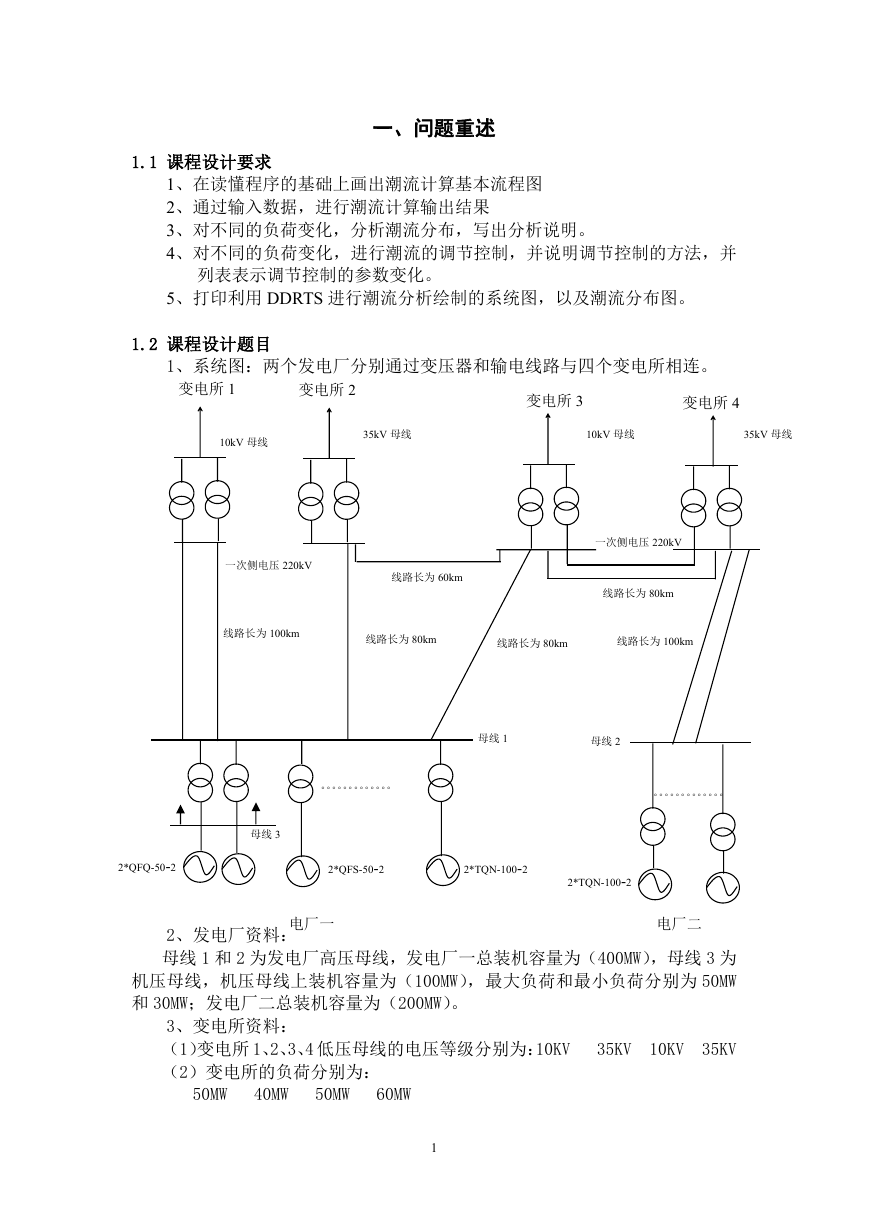
1、系统图：两个发电厂分别通过变压器和输电线路与四个变电所相连。
变电所 1
变电所 2
变电所 3
变电所 4
10kV 母线
35kV 母线
10kV 母线
35kV 母线
一次侧电压 220kV
线路长为 60km
一次侧电压 220kV
线路长为 80km
线路长为 100km
线路长为 80km
线路长为 80km
线路长为 100km
母线 1
母线 2
。。。。。。。。。。。。。
。。。。。。。。。。。。。
母线 3
2*QFQ-50-2
2*QFS-50-2
2*TQN-100-2
2*TQN-100-2
电厂一
电厂二
2、发电厂资料：
母线 1 和 2 为发电厂高压母线，发电厂一总装机容量为（400MW），母线 3 为
机压母线，机压母线上装机容量为（100MW），最大负荷和最小负荷分别为 50MW
和 30MW；发电厂二总装机容量为（200MW）。
3、变电所资料：
（1）变电所 1、2、3、4 低压母线的电压等级分别为：10KV
（2）变电所的负荷分别为：
50MW
40MW
50MW
60MW
35KV
10KV 35KV
1
（3）每个变电所的功率因数均为 cosφ=0.85；
（4）变电所 2 和变电所 4 分别配有两台容量为 75MVA 的变压器，短路损耗
414KW，短路电压（%）=16.7；变电所 1 和变电所 3 分别配有两台容量为 63MVA
的变压器，短路损耗为 245KW，短路电压（%）=10.5；
4、输电线路资料：
发电厂和变电所之间的输电线路的电压等级及长度标于图中，单位长度的电
阻为 17.0
，单位长度的电抗为
0.402 ，单位长度的电纳为
2.78
S-610*
。
1.3 课程设计基本内容
1. 对给定的网络查找潮流计算所需的各元件等值参数，画出等值电路图。
2. 输入各支路数据，各节点数据利用给定的程序进行在变电所在某一负荷
情况下的潮流计算，并对计算结果进行分析。
3. 跟随变电所负荷按一定比例发生变化，进行潮流计算分析。
1) 4 个变电所的负荷同时以 2%的比例增大；
2) 4 个变电所的负荷同时以 2%的比例下降
3) 1 和 4 号变电所的负荷同时以 2%的比例下降，而 2 和 3 号变电所的负荷
同时以 2%的比例上升；
4. 在不同的负荷情况下，分析潮流计算的结果，如果各母线电压不满足要
求，进行电压的调整。（变电所低压母线电压 10KV 要求调整范围在
9.5-10.5 之间；电压 35KV 要求调整范围在 35-36 之间）
5. 轮流断开环网一回线，分析潮流的分布。
6. 利用 DDRTS 软件，进行绘制系统图进行上述各种情况潮流的分析，并进
行结果的比较。
7. 最终形成课程设计成品说明书。
二、问题分析
2.1 节点设置及分类
根据系统图可知此系统为两端供电网路，将母线 1，2 设为节点 1，10，将
变电所 1、2、3、4 的高低压侧分别设为节点 2、3、4、5、6、7、8、9。并且，
将节点 1 设为平衡节点，将节点 10 设为 PV 节点，其余节点设为 PQ 节点。
S
B U
B
B
2
484
根据题目
2.2 参数求取
设定基准值
S B
100
MVA
，
U B
220
KV
，所以
Z
原始资料，计算发电厂、变压器及线路的参数。
（1）运用下列公式计算变压器参数：
R
T
k
2
N
UP
1000
S
2
N
UUX
2%
N
T 100
S
K
N
2
XRZ
T
T
T
ZZ
T
Z
T
B
（2）计算线路参数
Z
R
jX
(
r
)
Ljx
（3）变电所负荷分别为：
变电所 1
LS =50+j30.987 变电所 2
LS =40+j27.79
变电所 3
LS =50+j30.987 变电所 4
LS =60+j37.18
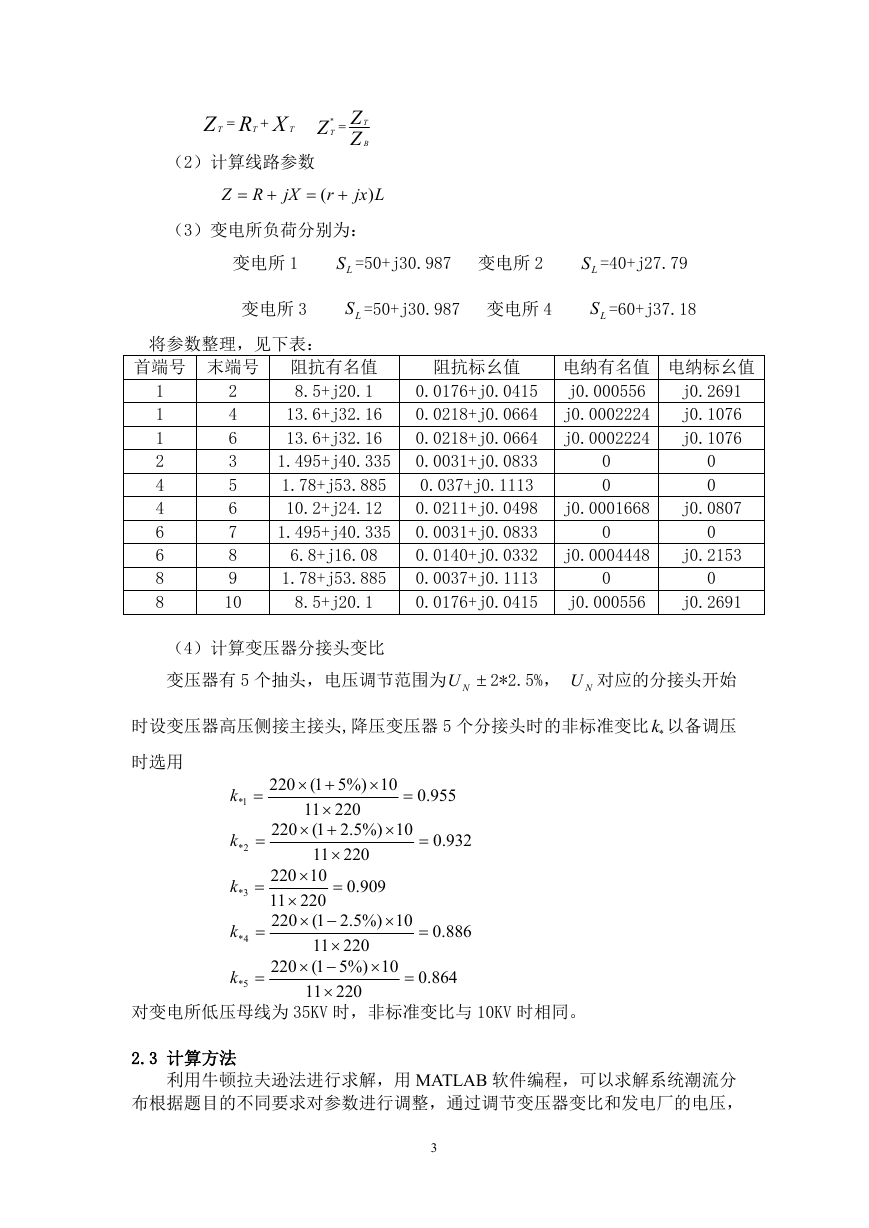
将参数整理，见下表：
首端号 末端号 阻抗有名值
8.5+j20.1
1
1
1
2
4
4
6
6
8
8
2
4
6
3
5
6
7
8
9
10
13.6+j32.16
13.6+j32.16
1.495+j40.335
1.78+j53.885
10.2+j24.12
1.495+j40.335
6.8+j16.08
1.78+j53.885
8.5+j20.1
阻抗标幺值
0.0176+j0.0415
0.0218+j0.0664
0.0218+j0.0664
0.0031+j0.0833
0.037+j0.1113
0.0211+j0.0498
0.0031+j0.0833
0.0140+j0.0332
0.0037+j0.1113
0.0176+j0.0415
电纳有名值 电纳标幺值
j0.000556
j0.0002224
j0.0002224
j0.2691
j0.1076
j0.1076
0
0
0
0
j0.0001668
j0.0807
0
0
j0.0004448
j0.2153
0
0
j0.000556
j0.2691
（4）计算变压器分接头变比
变压器有 5 个抽头，电压调节范围为 NU 2*2.5%， NU 对应的分接头开始
时设变压器高压侧接主接头,降压变压器 5 个分接头时的非标准变比 *k 以备调压
时选用
220
220
220
11
220
220
k
1*
k
2*
k
3*
k
4*
k
5*
220
220
.0
10%)51(
11
10%)5.21(
11
10
220
10%)5.21(
11
10%)51(
11
909
220
220
.0
955
.0
932
.0
886
.0
864
对变电所低压母线为 35KV 时，非标准变比与 10KV 时相同。
2.3 计算方法
利用牛顿拉夫逊法进行求解，用 MATLAB 软件编程，可以求解系统潮流分
布根据题目的不同要求对参数进行调整，通过调节变压器变比和发电厂的电压，
3
求解出合理的潮流分布，最后用 PSAT 进行潮流分析，将两者进行比较。
2.4 牛顿—拉夫逊法
1、牛顿—拉夫逊法概要
首先对一般的牛顿—拉夫逊法作一简单的说明。已知一个变量 X 函数为：
(
Xf
)
0
到此方程时，由适当的近似值
)0(
X 出发，根据：
(
n
)1
X
)(
n
X
(
Xf
(
Xf
)(
n
)(
n
)
)
(
n
2,1
,......)
反复进行计算，当
)(n
X 满足适当的收敛条件就是上面方程的根。这样的方
法就是所谓的牛顿—拉夫逊法。
这一方法还可以做下面的解释，设第 n 次迭代得到的解语真值之差，即
X
)(n
的误差为时，则：
nXf
(
)
)(
0
把
)( nXf
(
)
在
)(n
X 附近对用泰勒级数展开
(
Xf
)(
n
)
(
Xf
)(
n
)
(
Xf
)(
n
)
2
!2
(
Xf
)(
n
)
......
0
上式省略去 2 以后部分
(
Xf
)(
n
)
(
Xf
)(
n
)
0
)(n
X 的误差可以近似由上式计算出来。
(
Xf
(
Xf
)(
n
)(
n
)
)
)(n
X 的误差的一次项相等。
比较两式，可以看出牛顿—拉夫逊法的休整量和
用同样的方法考虑，给出 n 个变量的 n 个方程：
,
,
XXf
1
,
,
XXf
2
,
XXf
n
X
X
0
0
,
X
)
)
)
0
(
(
2
2
,
,
1
1
,
1
n
n
n
(
2
对其近似解 1X 得修正量 1X 可以通过解下边的方程来确定：
4
(
(
,
1
,
1
XXf
1
XXf
2
XXf
n
1
(
,
2
2
,
,
,
,
X
X
n
n
)
)
2
,
,
X
n
)
f
1
x
1
f
2
x
1
f
n
x
1
2
f
1
x
f
2
x
2
n
f
1
x
f
2
x
n
f
n
x
2
f
n
x
n
X
X
1
2
X
n
式中等号右边的矩阵
f
n
x
n
都是对于
,
XX
1 的值。这一矩阵称为雅可比
nX
2
,
,
（JACOBI）矩阵。按上述得到的修正向量
X
n
X
n
X
n
X
X
2
,
1
,
,
nX
后，得到如下关系
这比
,
XX
1 更接近真实值。这一步在收敛到希望的值以前重复进行，
nX
2
,
,
一般要反复计算满足
max
n
1
X
1
X
1
n
1
,
X
2
n
1
X
2
n
1
,
,
X
n
n
1
X
n
n
1
为预先规定的小正数， 1n
nX 是第 n 次迭代 nX 的近似值。
2、牛顿法的框图及求解过程
（1）用牛顿法计算潮流时，有以下的步骤：
①给这各节点电压初始值
)0(
e
, f
)0(
；
② 将 以 上 电 压 初 始 值 代 入 公 式 ， 求 修 正 方 程 的 常 数 项 向 量
)0(
P
,
Q
)0(
(,
V
)0(2
)
；
③将电压初始值在带入上述公式，求出修正方程中系数矩阵的各元素。
④解修正方程式
)0(
e
,
f
)0(
；
⑤修正各节点电压
)1(
e
)0(
e
e
)0(
，
f
)1(
f
)0(
f
)0(
；
⑥将 )1(e ， )1(f 在带入方程式，求出
⑦检验是否收敛，即
max
,
k
)
(
P
i
Q
i
)1(
Q
(,
V
)1(2
)
；
(
k
)1(
,
P
)
如果收敛，迭代到此结束，进一步计算各线路潮流和平衡节点功率，并打印
输出结果。如果不收敛，转回②进行下次迭代计算，直到收敛为止。
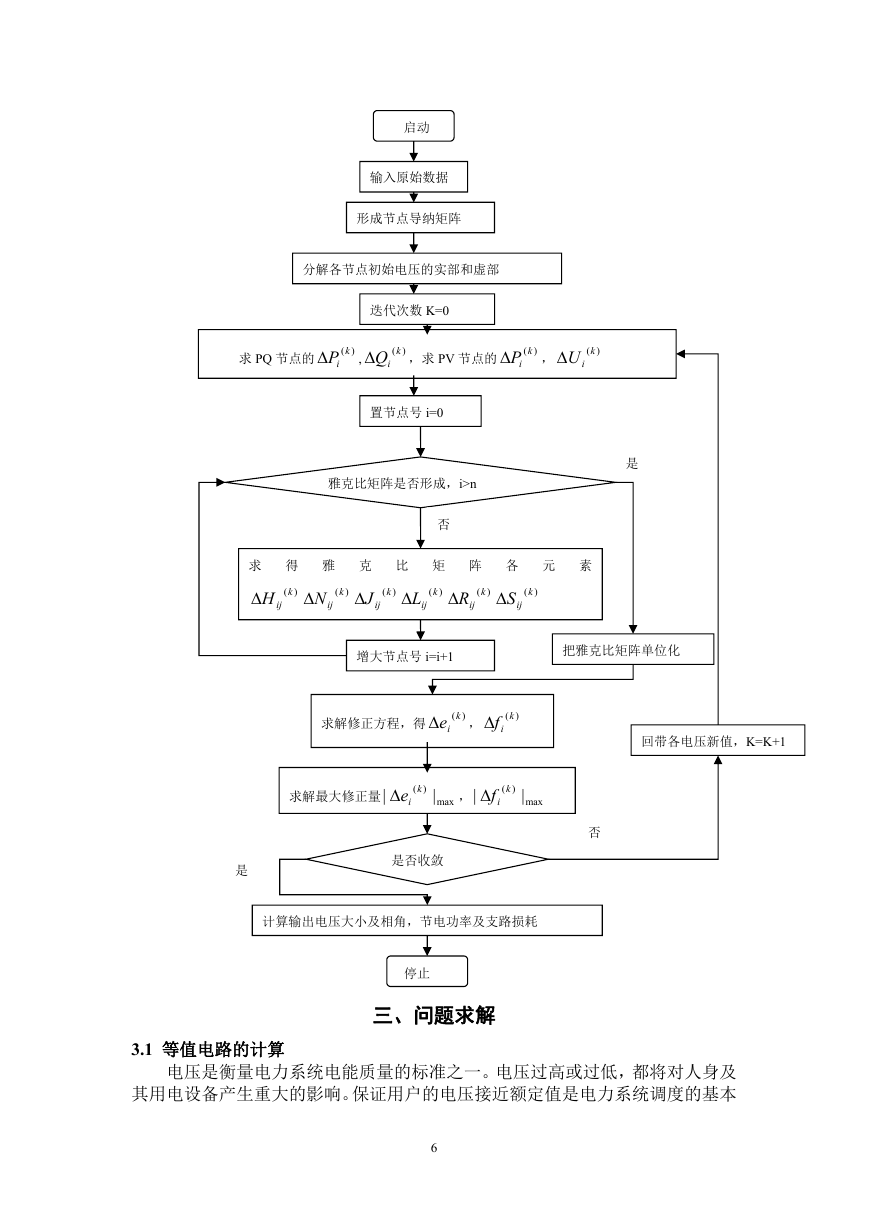
（2）程序框图如下：
5
启动
输入原始数据
形成节点导纳矩阵
分解各节点初始电压的实部和虚部
迭代次数 K=0
求 PQ 节点的
(k
)
iP
,
iQ
(k
)
，求 PV 节点的
(k
)
iP
，
iU
(k
)
置节点号 i=0
雅克比矩阵是否形成，i>n
否
是
求 得 雅 克 比 矩 阵 各 元 素
(k
)
ijH
(k
)
ijN
(k
)
ijJ
ijL
(k
)
ijR
(k
)
ijS
(k
)
增大节点号 i=i+1
把雅克比矩阵单位化
求解修正方程，得
(k
)
ie
，
if
(k
)
回带各电压新值，K=K+1
求解最大修正量
(
k
)
|
ie
|
max
，
|
if
(
k
)
|
max
否
是
是否收敛
计算输出电压大小及相角，节电功率及支路损耗
停止
三、问题求解
3.1 等值电路的计算
电压是衡量电力系统电能质量的标准之一。电压过高或过低，都将对人身及
其用电设备产生重大的影响。保证用户的电压接近额定值是电力系统调度的基本
6
任务之一。当系统的电压偏离允许值时，电力系统必须应用电压调节技术调节系
统电压的大小，使其维持在允许值范围内。本文经过手算形成了等值电路图，并
编写好了程序得出节点电压标幺值，使其满足所要求的调整范围。
我们首先对给定的程序输入部分作了简要的分析，程序开始需要我们确定输
入节点数、支路数、平衡母线号、支路参数矩阵、节点参数矩阵。
（1）为了保证整个系统潮流计算的完整性，我们把凡具有母线及发电机处
均选作节点，这样，可以确定有 10 个节点，节点号见等值电路图。
（2）确定完节点及编号后，各条支路也相应确定了，网络中总计有 13 条支
路，我们对各支路参数进行了计算。根据所给实际电路图和题中的已知条件，有
以下公式计算各输电线路的阻抗和对地支路电容的标幺值和变压器的阻抗标幺
值。选择电压基准值为
BU
220
KV
和功率基准值
BS
100
MVA
所以
Z
B
U
S
B
B
484
3.2 依据题目要求及原始资料画出系统等值电路图：
3
S=50+j30.987
5
S=40+j27.79
7
S=50+j30.987
9
S=40+j24.8
1.495+j40.335
1.78+j53.885
1.495+j40.335
1.78+j53.885
1
:
k
1
2
1
:
k
2
4
1
:
k
3
6
1
:
k
4
8
10.2+j24.12
6.8+j16.08
8.5+j20.1
j 0.000556
4
10
U=231V
P=200MW
发电厂二
8.5+j20.1
j0.0000834
13.6+j32.16
j 0.0004448
13.6+j32.16
j0.0001112
j 0.000556
j0.0001112
1
发电厂一
δ=0
U=231V
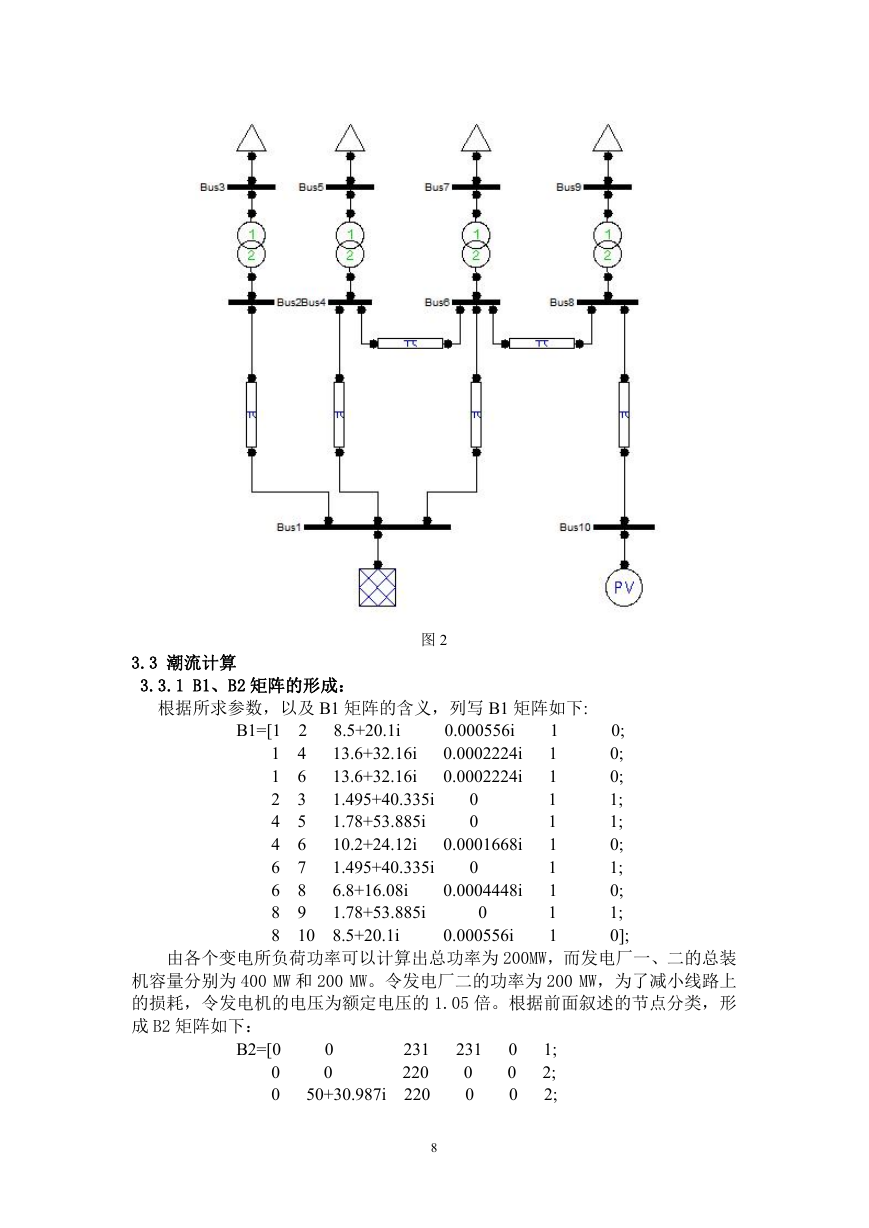
利用 psat 软件可得计算所需系统图如图 2 所示。
图 1 系统等值电路
7
3.3 潮流计算
3.3.1 B1、B2 矩阵的形成：
图 2
根据所求参数，以及 B1 矩阵的含义，列写 B1 矩阵如下:
1
1
1
1
1
1
1
1
1
1
0;
0;
0;
1;
1;
0;
1;
0;
1;
0];
B1=[1 2
4
6
3
5
6
7
8
9
10
1
1
2
4
4
6
6
8
8
8.5+20.1i
13.6+32.16i
13.6+32.16i
1.495+40.335i
1.78+53.885i
10.2+24.12i
1.495+40.335i
6.8+16.08i
1.78+53.885i
8.5+20.1i
0.000556i
0.0002224i
0.0002224i
0
0
0
0.0001668i
0.0004448i
0
0.000556i
由各个变电所负荷功率可以计算出总功率为 200MW，而发电厂一、二的总装
机容量分别为 400 MW 和 200 MW。令发电厂二的功率为 200 MW，为了减小线路上
的损耗，令发电机的电压为额定电压的 1.05 倍。根据前面叙述的节点分类，形
成 B2 矩阵如下：
B2=[0
0
0
0
0
50+30.987i
231
220
220
231
0
0
0
0
0
1;
2;
2;
8
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
