数学建模论文三：仓库选址问题 金融统计 121 范子君 1202103022 1.问题的提出 某地区有 n（n≥2）个商品粮生产基地,各基地的粮食数量分别 为 m1、m2、…、mn(单位：吨），每吨粮食一距离单位运费为 c,为使 各基地到仓库的总运费最小,问仓库如何选址? 2.模型的假设 ⑴各商品粮生产基地的粮食集中于一处； ⑵各商品粮生产基地及仓库看作点； ⑶各商品粮生产基地与仓库之间道路按直线段考虑。 3.模型的建立 建立平面直角坐标系 xOy，各商品粮生产基地的坐标 分别为（xi,yi),i=1,2, …,n;仓库的坐标为（x,y),则各商品粮 生产基地到仓库的总运费为 n  i  1 ( yxf , )  于是模型为 cm i ( x  x i 2 )  ( y  y i 2 ) 

cm i ( x  x i 2 )  ( y  y i 2 ) )1( n  i  1 min , yx ( yxf , )  4.模型的求解 由 有        n   i  1 i 1  n ) ,( yxf  x   ,0 ) ,( yxf  y   0 i ( xm i 2 ) x  ( ym i 2 ) x  i     x i ( y y i ( y )  )  y i 2 ) y i 2 )  0  0 )2( ( x ( x 对一般 n 求解方程组（2）有一定困难！但 n=2 时比较容易求得 仓库坐标       * 22 xmxmx 11  mm 1 2 ymymy 11 22  mm 2     * 1 )3( 

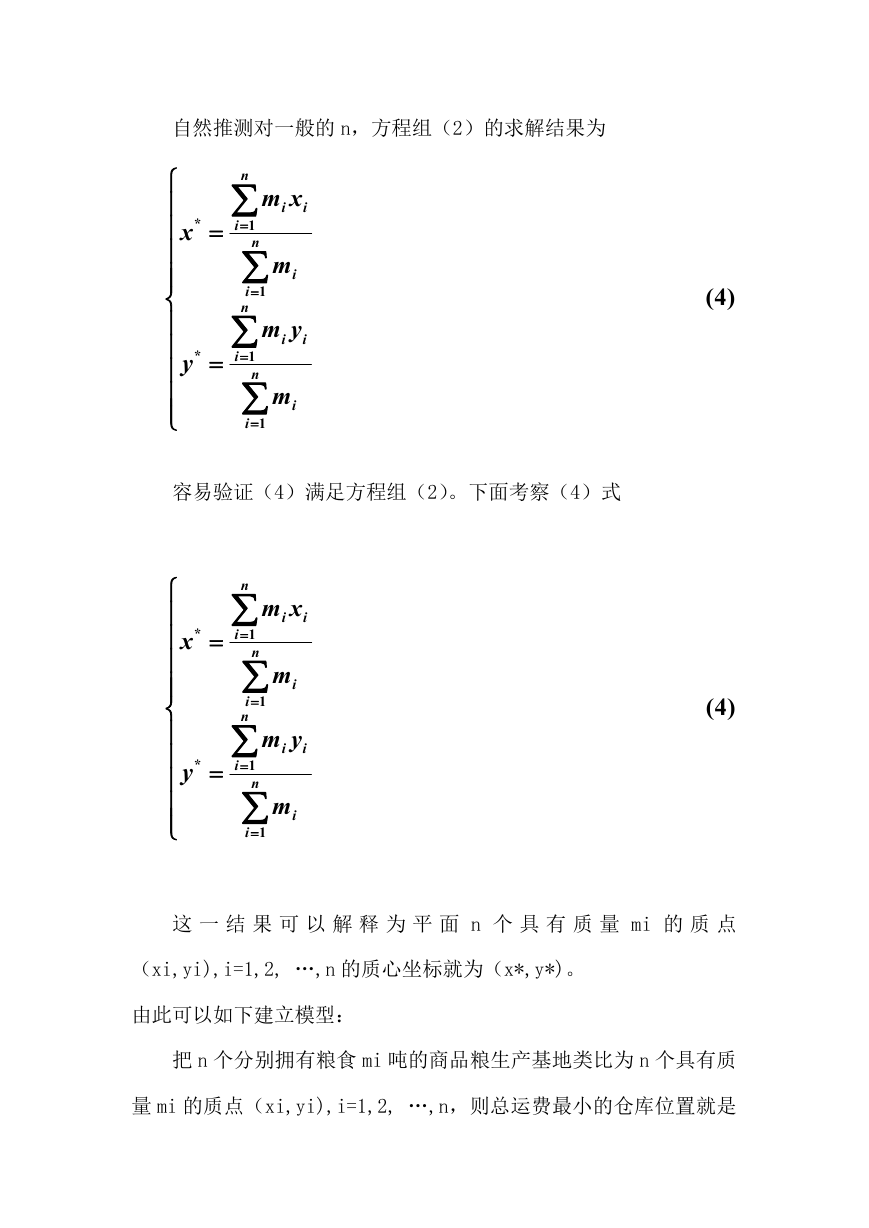
自然推测对一般的 n，方程组（2）的求解结果为 * x  * y              xm i m i 1 ym i n i   1 n     1 n i n  i i  1 m i i i i i 容易验证（4）满足方程组（2）。下面考察（4）式 * x  * y              xm i m i 1 ym i n i   1 n     1 n i n  i i  1 m i )4( )4( 这 一 结 果 可 以 解 释 为 平 面 n 个 具 有 质 量 mi 的 质 点 （xi,yi),i=1,2, …,n 的质心坐标就为（x*,y*)。 由此可以如下建立模型： 把 n 个分别拥有粮食 mi 吨的商品粮生产基地类比为 n 个具有质 量 mi 的质点（xi,yi),i=1,2, …,n，则总运费最小的仓库位置就是 

这 n 个质点的质心（x*,y*)。