计算机控制系统习题答案.pdf-资料库

习题及部分习题解答第 1 章习题 1-1 举例说明 2~3 个你熟悉的计算机控制系统，并说明与常规连续模拟控制系统相比的优点。 1-2 利用计算机及接口技术的知识，提出一个用同一台计算机控制多个被控参量的分时巡回控制方案。 1-3 题图 1-3 是模拟式雷达天线俯仰角位置伺服控制系统原理示意图，试把该系统改造为计算机控制系统，画出原理示意图及系统结构图。题图 1-3 模拟式雷达天线俯仰角位置伺机控制系统原理示意图 1-4 水位高度控制系统如题图 1-4 所示。水箱水位高度指令由 W1 电位计指令电压 ur 确定，水位实际高度 h 由浮子测量，并转换为电位计 W2 的输出电压 uh。用水量 Q1 为系统干扰。当指令高度给定后，系统保持给定水位，如打开放水管路后，水位下降，系统将控制电机，打开进水阀门，向水箱供水，最终保持水箱水位为指令水位。试把该系统改造为计算机控制系统。画出原理示意图及系统结构图。题图 1-4 水箱水位控制系统原理示意图 d-1

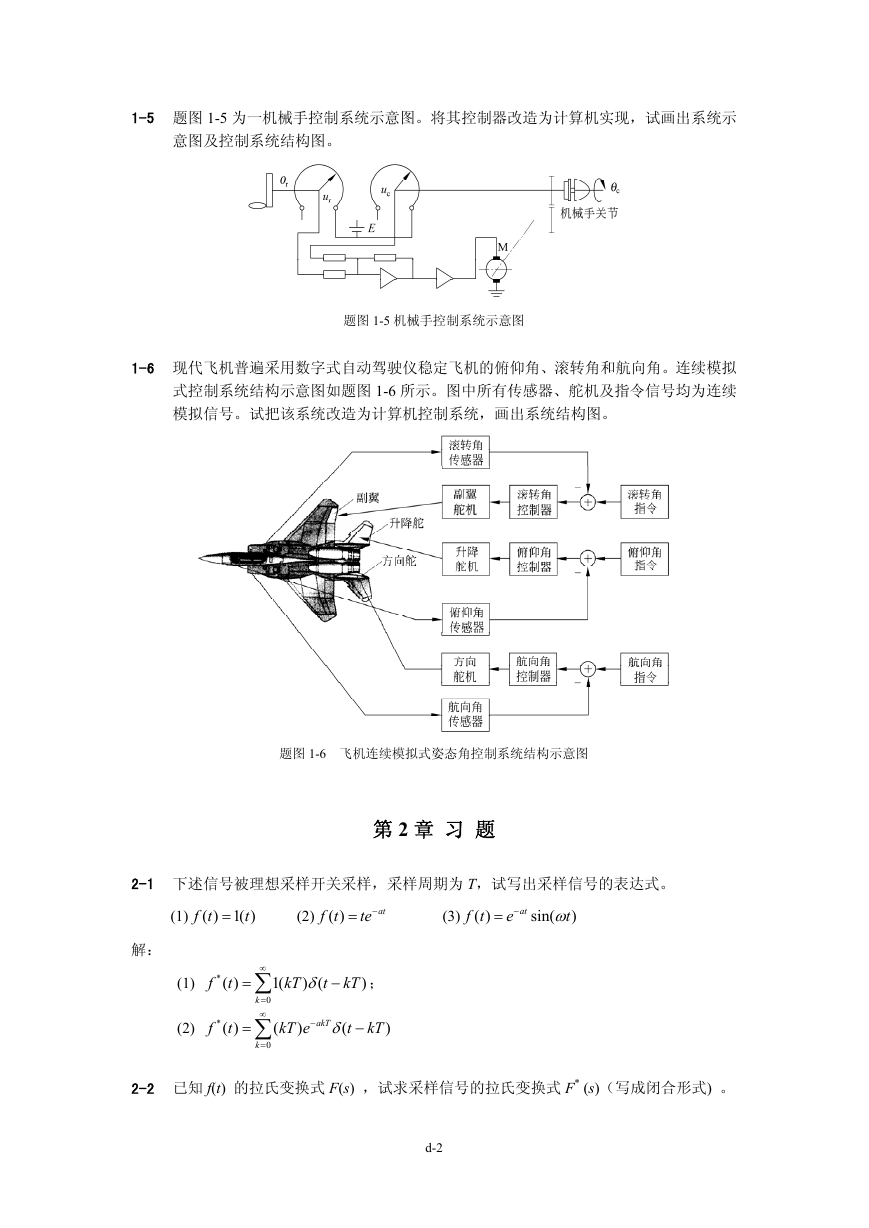
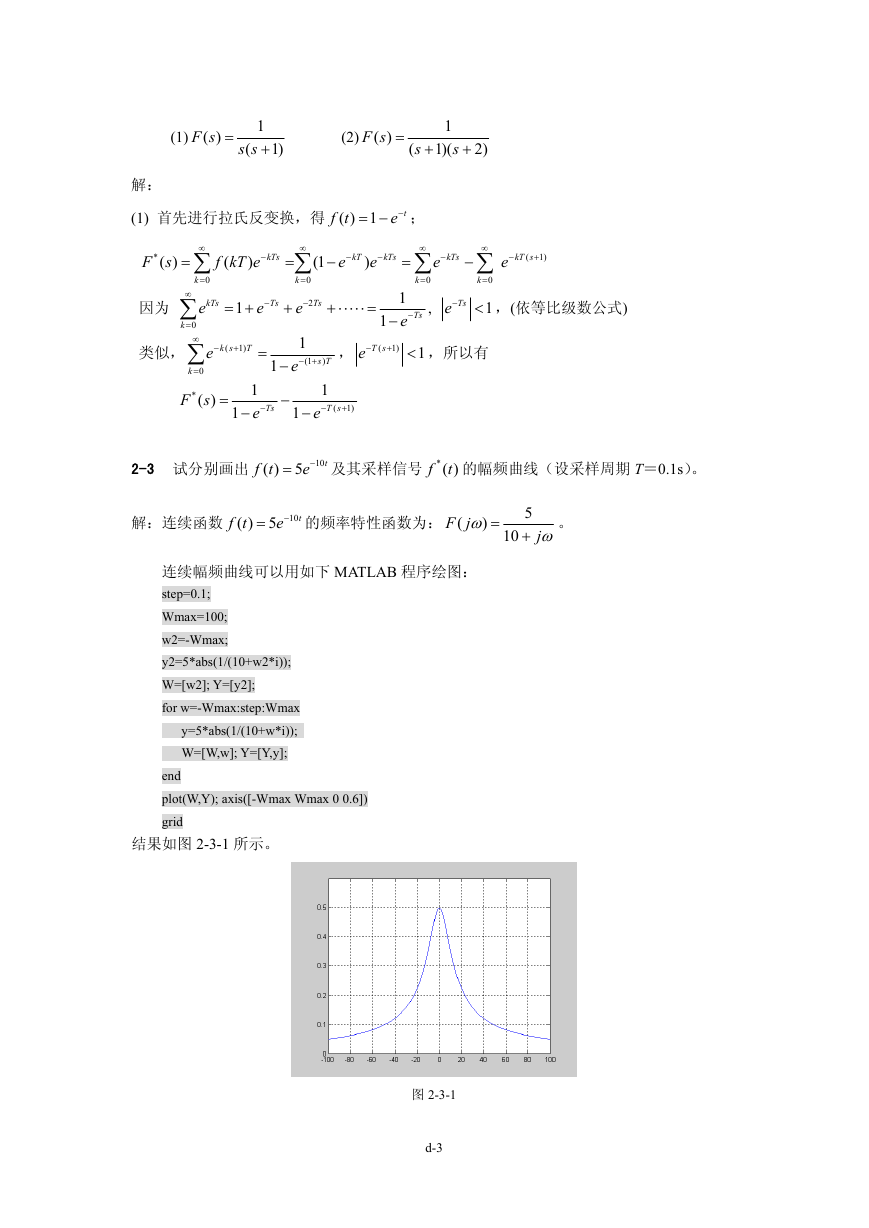
1-5 题图 1-5 为一机械手控制系统示意图。将其控制器改造为计算机实现，试画出系统示意图及控制系统结构图。题图 1-5 机械手控制系统示意图 1-6 现代飞机普遍采用数字式自动驾驶仪稳定飞机的俯仰角、滚转角和航向角。连续模拟式控制系统结构示意图如题图 1-6 所示。图中所有传感器、舵机及指令信号均为连续模拟信号。试把该系统改造为计算机控制系统，画出系统结构图。题图 1-6 飞机连续模拟式姿态角控制系统结构示意图第 2 章习题 2-1 下述信号被理想采样开关采样，采样周期为 T，试写出采样信号的表达式。 (1) f t t= ( ) 1( ) (2) f t ( ) te−= at (3) f t ( ) tω−= sin( e at ) 解： (1) f * t ( ) = (2) f * t ( ) = ∞ ∑ 0 k = ∞ ∑ = 0 k 1( kT t ) ( δ − kT ) ； ( kT e ) − akT t ( δ − kT ) 2-2 已知 f(t) 的拉氏变换式 F(s) ，试求采样信号的拉氏变换式 F* (s)（写成闭合形式) 。 d-2

(1) F s ( ) = 1 s s ( + 1) (2) F s ( ) = 1 1)( s + 2) ( s + 解： (1) 首先进行拉氏反变换，得 ( ) 1 = − ； e− f t t * F s ( ) = f kT e ) ( − kTs = − kT s ( 1) + e ∞ ∑ 0 (1 − e − kT ) e − kTs = ∞ ∑ = 0 k − kTs e − k = e 2 − Ts + ⋅⋅⋅⋅⋅ = 1 e 1 − , − Ts ∞ ∑ k 0 = 1 ∞ ∑ k 0 = e ∞ ∑ k = 0 ∞ ∑ = 0 k 因为 kTs 1 = + e − Ts + Tse− < ，(依等比级数公式) 类似， − k s ( 1) + T e = 1 (1 − + s T ) 1 − e e− T s ， ( 1) + < ，所以有 1 * F s ( ) = 1 e 1 − − − Ts 1 − e 1 T s ( − 1) + 2-3 试分别画出 f t ( ) 5 = e− 10 t 及其采样信号 *( ) t 的幅频曲线（设采样周期 T＝0.1s）。 f 解：连续函数 f t ( ) 5 = e− 10 t 的频率特性函数为： F j ( ) ω = 5 + 10 。 j ω 连续幅频曲线可以用如下 MATLAB 程序绘图： step=0.1; Wmax=100; w2=-Wmax; y2=5*abs(1/(10+w2*i)); W=[w2]; Y=[y2]; for w=-Wmax:step:Wmax y=5*abs(1/(10+w*i)); W=[W,w]; Y=[Y,y]; end plot(W,Y); axis([-Wmax Wmax 0 0.6]) grid 结果如图 2-3-1 所示。图 2-3-1 d-3

该函数的采样信号幅频谱数学表达式为 ∞ ∑ F j ( ) ω = * 1 T F j ( )s ω ω jn + * F J ( ω s ) ≈ 1 T ∞ ∑ n =−∞ n =−∞ jn F j ( ω ω s + ) ≈ 1 T N ∑ n =− N 显然，采用的项数 N 越大，则计算得到的值越逼近于实际值。这里采用 9N = 来进行 F j ( ω ω s + jn ) 计算。采样幅频曲线可以用如下 MATLAB 程序绘图： %采样周期 %每个采样周期的计算点数 %计算步长 %画图显示的频率范围 %采样频率 T=0.1; ws=2*pi/T; num=50; step=ws/num; Wmax=150; GW=4*Wmax; %计算的频率范围 g0=(1/T)*5*abs(1/(1+10*GW*i)); G00=[g0]; g0=(1/T)*5*abs(1/(10+(GW+ws)*i)); G11=[g0]; g0=(1/T)*5*abs(1/(10+(GW-ws)*i)); G12=[g0]; g0=(1/T)*5*abs(1/(10+(GW+2*ws)*i)); G21=[g0]; g0=(1/T)*5*abs(1/(10+(GW-2*ws)*i)); G22=[g0]; g0=(1/T)*5*abs(1/(10+(GW+3*ws)*i)); G31=[g0]; g0=(1/T)*5*abs(1/(10+(GW-3*ws)*i)); G32=[g0]; g0=(1/T)*5*abs(1/(10+(GW+4*ws)*i)); G41=[g0]; g0=(1/T)*5*abs(1/(10+(GW-4*ws)*i)); G42=[g0]; g0=(1/T)*5*abs(1/(10+(GW+5*ws)*i)); G51=[g0]; g0=(1/T)*5*abs(1/(10+(GW-5*ws)*i)); G52=[g0]; g0=(1/T)*5*abs(1/(10+(GW+6*ws)*i)); G61=[g0]; g0=(1/T)*5*abs(1/(10+(GW-6*ws)*i)); G62=[g0]; g0=(1/T)*5*abs(1/(10+(GW+7*ws)*i)); G71=[g0]; g0=(1/T)*5*abs(1/(10+(GW-7*ws)*i)); G72=[g0]; g0=(1/T)*5*abs(1/(10+(GW+8*ws)*i)); G81=[g0]; g0=(1/T)*5*abs(1/(10+(GW-8*ws)*i)); G82=[g0]; g0=(1/T)*5*abs(1/(10+(GW+9*ws)*i)); G91=[g0]; g0=(1/T)*5*abs(1/(10+(GW-9*ws)*i)); G92=[g0]; 其余类似，最后可得，结果如图 2-3-2 所示。 10 8 6 4 2 0 -150 -100 -50 0 50 100 150 图 2-3-2 d-4

2-4 若数字计算机的输入信号为 f t ( ) 5 = e− 10 t ，试根据采样定理选择合理的采样周期 T，设 F j 信号中的最高频率为 mω 定义为 ( ω = ) m 0.1 (0) F 。解： F s ( ) = 5 10 + s ； F j ( ) ω = 5 j ω + 10 ；所以有 5 + 2 ω max 2 10 = 0.1 (0) F = 0.1 5 × 10 = 0.05 ， 0.05 ( 2 ω + 2 max 2 10 ) 25 = 由此可得依采样定理得： ω = max 99.5 ； sω ω> max 2 = 199 rad/s。 2-5 已知信号 x＝ A cos( tω ，试画出该信号的频谱曲线以及它通过采样器和理想滤波器以 ) 1 后的信号频谱。设采样器的采样频率分别为 4ω1，1.5ω1，和ω1 这 3 种情况。解释本题结果。 cos( )tω 的频谱为脉冲，如题图 2-5-1 所示。 1 解： d-5

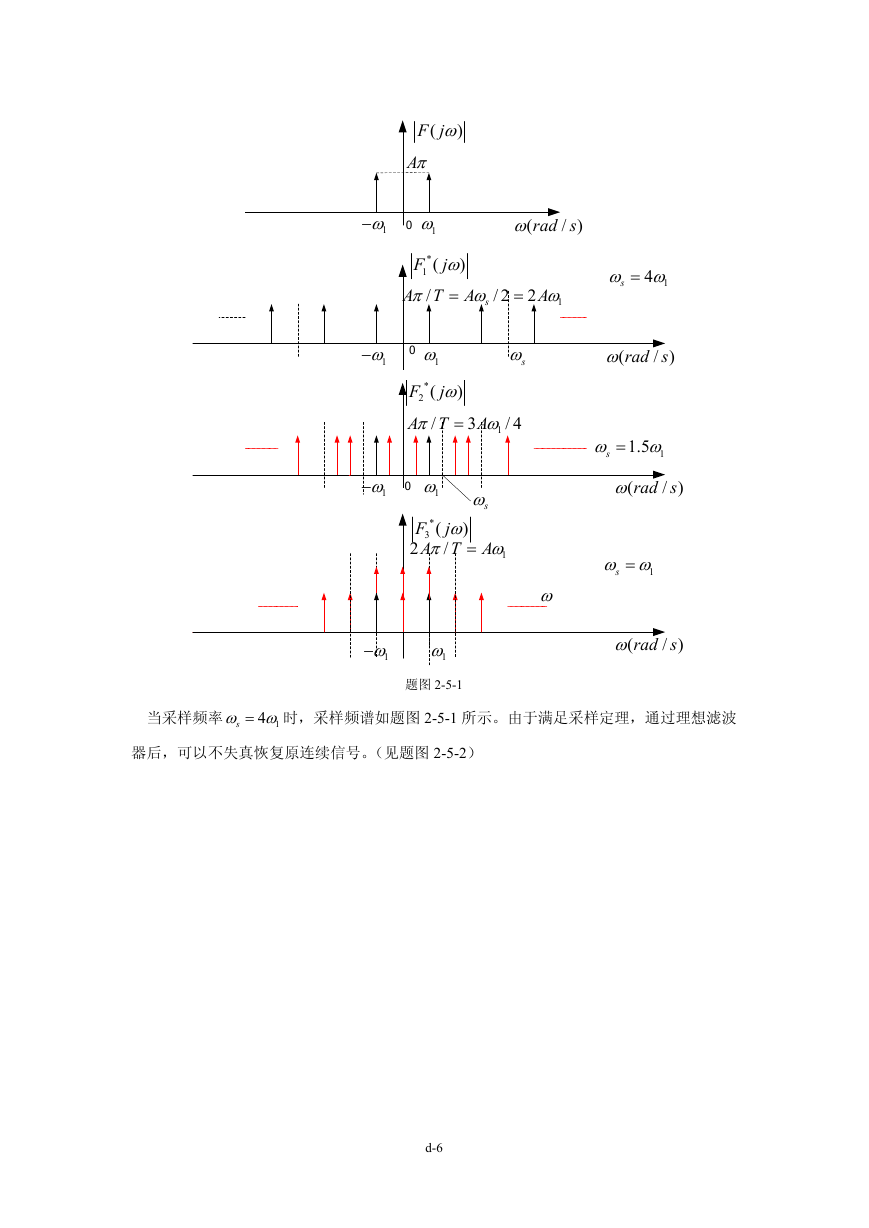
F jω ( ) πA 1ω− 0 1ω rad sω / ) ( )ωF j 1 ( * A A T / ω π = s / 2 = 2 A ω 1 1ω− 0 1ω )ωF j 2 ( * A T / π ω= 1 A 3 sω / 4 1ω− 0 1ω sω )ωF j 3 ( * A T /π 2 ω= 1 A 1ω− 1ω 题图 2-5-1 14 sω ω= rad sω / ) ( sω ω= 1 1.5 rad sω / ) ( sω ω= 1 ω rad sω / ) ( 当采样频率 sω ω= 时，采样频谱如题图 2-5-1 所示。由于满足采样定理，通过理想滤波 14 器后，可以不失真恢复原连续信号。（见题图 2-5-2） d-6

hF jω ) ( πA 14 sω ω= 1ω1ω− o / 2sω rad sω / ) ( hF jω 2( ) πA o 1 / 2ω hF jω 3( ) 2Aπ o 题图 2-5-2 sω ω= 1 1.5 rad sω / ) ( sω ω= 1 rad sω / ) ( 当采样频率 sω ω= 1 1.5 时，采样频谱如题图 2-5-1 所示。由于不满足采样定理，采样频率发生折叠，当通过理想滤波器后，只保留了折叠后的低频信号，其频率为 1.5 − 1 ω ω ω 1 0.5 = 1 。（见题图 2-5-2）当采样频率 sω ω= 时，采样频谱如题图 2-5-1 所示。由于不满足采样定理，采样频率发生折叠，折叠后的低频信号位于 0ω= 处，当通过理想滤波器后，只保留了折叠后的低频信号，其频率为 0ω= ，即直流信号。（见题图 2-5-2） 1 2-6 已知信号 x A = cos( tω 1 ) ，通过采样频率 sω ω= 的采样器以后．又由零阶保持器恢复 13 成连续信号，试画出恢复以后信号的频域和时域曲线；当 sω ω= 1 10 时，情况又如何? 比较结果。解：本题信号的频谱为脉冲，如题图 2-6(a)所示。 d-7

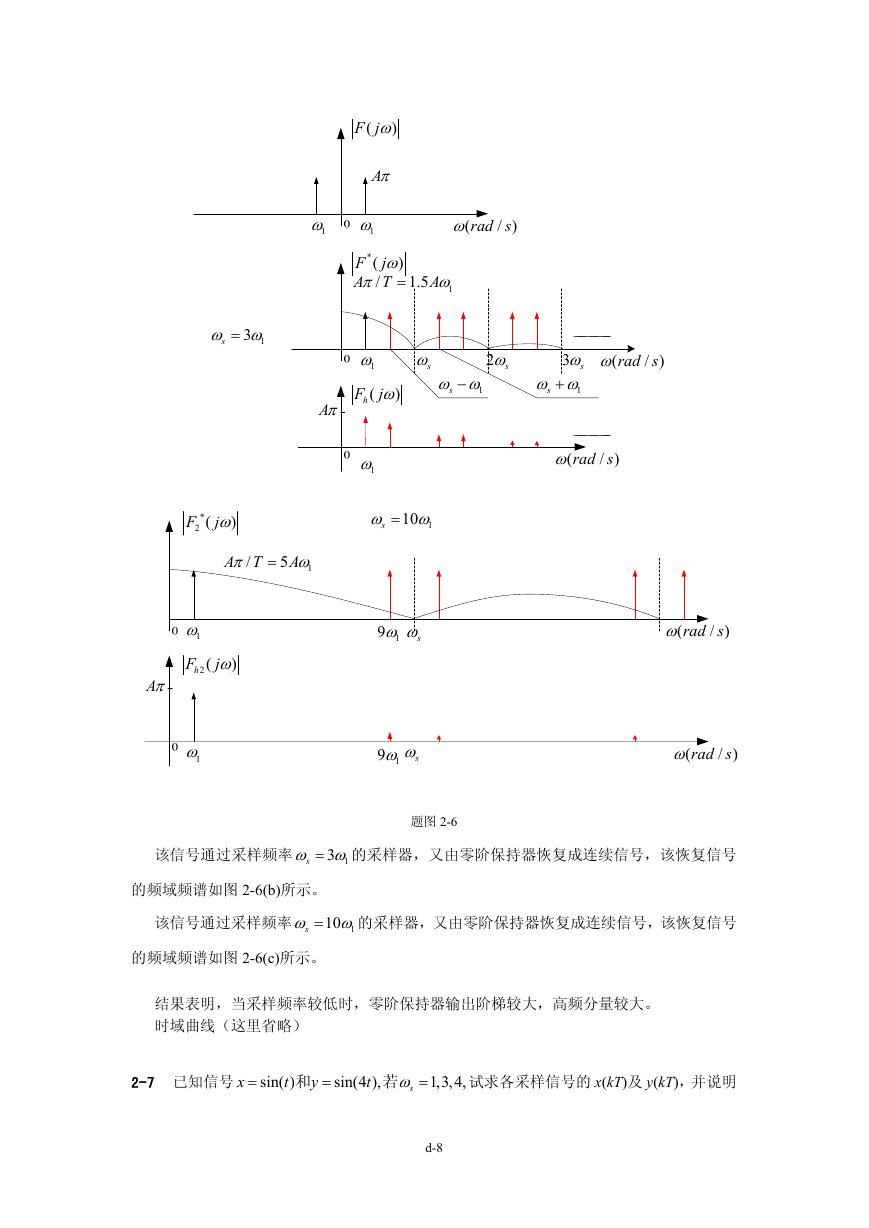
F jω ) ( πA 1ω1ω rad sω / ) ( F jω *( ) A T / ω= π 1 1.5 A 13 sω ω= )ωF j 2 ( * A T / π 1ω )ωhF j 2( πA 1ω ω= 1 A 5 1ω )ωhF j ( πA sω 2 sω sω ω− 1 3 sω sω ω+ 1 rad sω / ) ( rad sω / ) ( 1ω sω ω= 1 10 19ω sω rad sω / ) ( 19ω sω 题图 2-6 rad sω / ) ( 该信号通过采样频率 sω ω= 的采样器，又由零阶保持器恢复成连续信号，该恢复信号 13 的频域频谱如图 2-6(b)所示。该信号通过采样频率 sω ω= 1 10 的采样器，又由零阶保持器恢复成连续信号，该恢复信号的频域频谱如图 2-6(c)所示。结果表明，当采样频率较低时，零阶保持器输出阶梯较大，高频分量较大。时域曲线（这里省略） 2-7 已知信号 sin( ) t = x y 和 = sin(4 ), t ω s 若 = 1,3,4, 试求各采样信号的 x(kT)及 y(kT)，并说明 d-8

资料库

计算机控制系统习题答案.pdf

相关推荐

课程资源

热门标签

最新资料