138 2016，52（22） Computer Engineering and Applications 计算机工程与应用 声源定位中广义互相关时延估计算法的研究 茅惠达，张玲华 MAO Huida, ZHANG Linghua 南京邮电大学 通信与信息工程学院，南京 210003 College of Telecommunications & Information Engineering, Nanjing University of Post and Telecommunications, Nanjing 210003, China MAO Huida, ZHANG Linghua. Research on generalized cross correlation algorithm for time delay estimation in sound source localization. Computer Engineering and Applications, 2016, 52（22）：138-142. Abstract：Sound source localization based on Time Delay Estimation（TDE）is one of the core of the algorithm in hearing aids. However, the estimation accuracy is often affected by the sampling rate and noise, which leads to the inaccuracy of location. In order to solve the problem, in this paper, combined with Fine Interpolation of Correlation Peak method （FICP）, an improved generalized cross correlation algorithm based on second correlation is proposed. In the proposed method, second correlation is adopted to reduce the interference of noise, FICP is used to improve the resolution of corre- lation function. The simulation results show that under both low SNR and high SNR environments, the proposed method can improve the performance of time delay estimation significantly. Key words：time delay estimation; generalized cross correlation; second correlation; fine interpolation of correlation peak 摘 要：基于时延估计（TDE）的声源定位算法是数字助听器中的核心算法之一，其估计精度会受到噪声和采样频率 等因素的影响，导致了定位的不准确性。针对这一问题，结合相关峰精确插值算法（FICP），提出了一种基于二次相 关改进的广义互相关时延估计算法。该算法通过二次相关，有效地降低噪声的干扰，再利用 FICP，提高相关函数的 分辨率。仿真实验表明，无论在低信噪比，还是在高信噪比环境下，改进算法的时延估计性能都有了明显改善。 关键词：时延估计；广义互相关；二次相关；相关峰精确插值 文献标志码：A 中图分类号：TP391 doi：10.3778/j.issn.1002-8331.1501-0090 1 引言 声源定位技术是数字助听器中的一项关键技术，它 利用麦克风阵列对声音信号进行采集，并通过对采集到 的信号进行处理从而得到声源位置。目前声源定位技 术主要分为三类 [1]：（1）基于高分辨率谱估计的定位方 法；（2）基于最大输出功率的可控波束形成的定位方法； （3）基于到达时间差（Time Delay Of Arrival，TDOA）的 定位方法。由于基于 TDOA 的声源定位技术不但可以 实现对声源的快速定位，而且计算量小，成为了数字助 听器中首选的定位方法[2-3]。 基于 TDOA 的定位算法是一种双步定位算法，它首 先估计声源到达不同麦克风的时间差，再利用得到的时 延，结合麦克风阵列的结构，确定声源的位置[4]。广义互 相 关 法（Generalized Cross Correlation，GCC）[5]是 一 种 最常用的时延估计算法，它通过计算两路信号的互相关 函数，其峰值就是 TDOA 估计值。然而 GCC 是基于理 想的信号传输模型，实际中不仅受噪声和混响的影响， 还受到采样频率的限制，TDOA 估计精度不高。随后， 文献[6-8]分别对其作出了改进。文献[6]提出了倒谱滤 波 技 术（Cepstral Prefiltering，CEP），它 利 用 通 道 的 特 性，有效地去除信号中受反射影响的部分，再将滤波后的 信号通过 GCC 进行 TDOA 估计。文献[7]提出了基音加 基金项目：江苏省高校自然科学研究重大项目（No.13KJA510003）；江苏高校优势学科建设工程资助项目（PAPD）。 作者简介：茅惠达（1990—），男，硕士研究生，主要研究方向为现代语音处理与通信技术，E-mail：maohui-da2009@126.com；张玲华 （1964—），女，博士，教授，博士生导师，主要研究方向为语音信号处理、智能信号处理等。 收稿日期：2015-01-07 修回日期：2015-02-13 文章编号：1002-8331（2016）22-0138-05 CNKI 网络优先出版：2015-07-03, http://www.cnki.net/kcms/detail/11.2127.TP.20150703.1656.031.html 

茅惠达，张玲华：声源定位中广义互相关时延估计算法的研究 2016，52（22） 139 权的 GCC 法，比较适合准周期的语音信号。文献[8]提 出了双耳电平差法（Interaural Level Difference，ILD）， 通过提取先于反射分量到达人耳的语音段来求 GCC， 有效抑制混响的影响。这些方法虽然能够取得较好的 TDOA 估计效果，但算法复杂，计算量大，实时处理比较 困难。因此，实用中一直在对 GCC 进行研究与改进。 本文在 GCC 的基础上，结合 FICP，提出了一种基于 二次相关改进的广义互相关时延估计算法。仿真实验 表明，改进算法取得了较好的 TDOA 估计效果。 2 广义互相关时延估计算法 假设两个麦克风接收的信号模型为： x 1 x s(n) + n (n) 1 s(n - d) + n (n) = α 1 (n) = α (n) 2 2 2 (n)、n 其中，s(n) 是声源信号，d 为时延，α 、α 1 (n) 是高斯白噪声信号。 因子，n 2 1 (n) 的互相关函数表示为： (n)、x (τ) = E[x (n)x 1 (τ - d) + R (τ - d) + R (n + τ)]= x 1 R R 12 2 2 2 ss sn 1 （1） （2） 是信号的衰减 (τ) + R (τ) （3） n n 1 2 sn 2 又假设信号与噪声、噪声与噪声之间互不相关，则： R (τ - d) = R (τ) = R (τ) = 0 2 2 n n 1 sn 1 sn 式（3）化简为： (τ - d) （5） R 由相关函数的性质可知，当 τ = d 时互相关函数取 (τ) = R 12 ss （4） 得最大值。根据以上的分析，d 就是 TDOA 估计值。 实际中由于噪声和混响的影响，会出现虚假的峰， 造成估计误差。因此提出了广义互相关法，它将互相关 函数变换到频域，对其互功率谱进行加权，增强信号中 信噪比较高的频率成分，从而抑制噪声的影响，再反变 换到时域，得到广义互相关（GCC）函数，即： R x 2 x 1 其中 G x x 1 2 π ψ (ω)G (τ) =  (ω) 是接收信号 x 1 x 1 12 0 x 2 是广义互相关加权函数。 (ω)e-jωπdω （6） (n)、x 2 (n) 的互功率谱，ψ 12 (ω) 3 改进的广义互相关时延估计算法 在强信噪比环境下，相位变换加权广义互相关算法 （GCC-PHAT）对 于 宽 带 准 周 期 的 语 音 信 号 ，相 关 峰 尖 锐，时延估计效果最好，但随着信噪比的下降，估计性能 下降很快[9]。为了提高抗噪声性能，文献[6-8，10]提出了 一些基于语音特性、通道传递函数、人耳感知特性的改 进算法，但算法都复杂，计算量大，不满足数字助听器实 时性要求。文献[11-12]提出二次相关算法来抑制噪声 (n) 作自相 的干扰，取得了很好的效果。该算法先对 x 1 关得到 R (τ) ，最 后对 R 12 (τ) 作互相关，得到二次相关函数。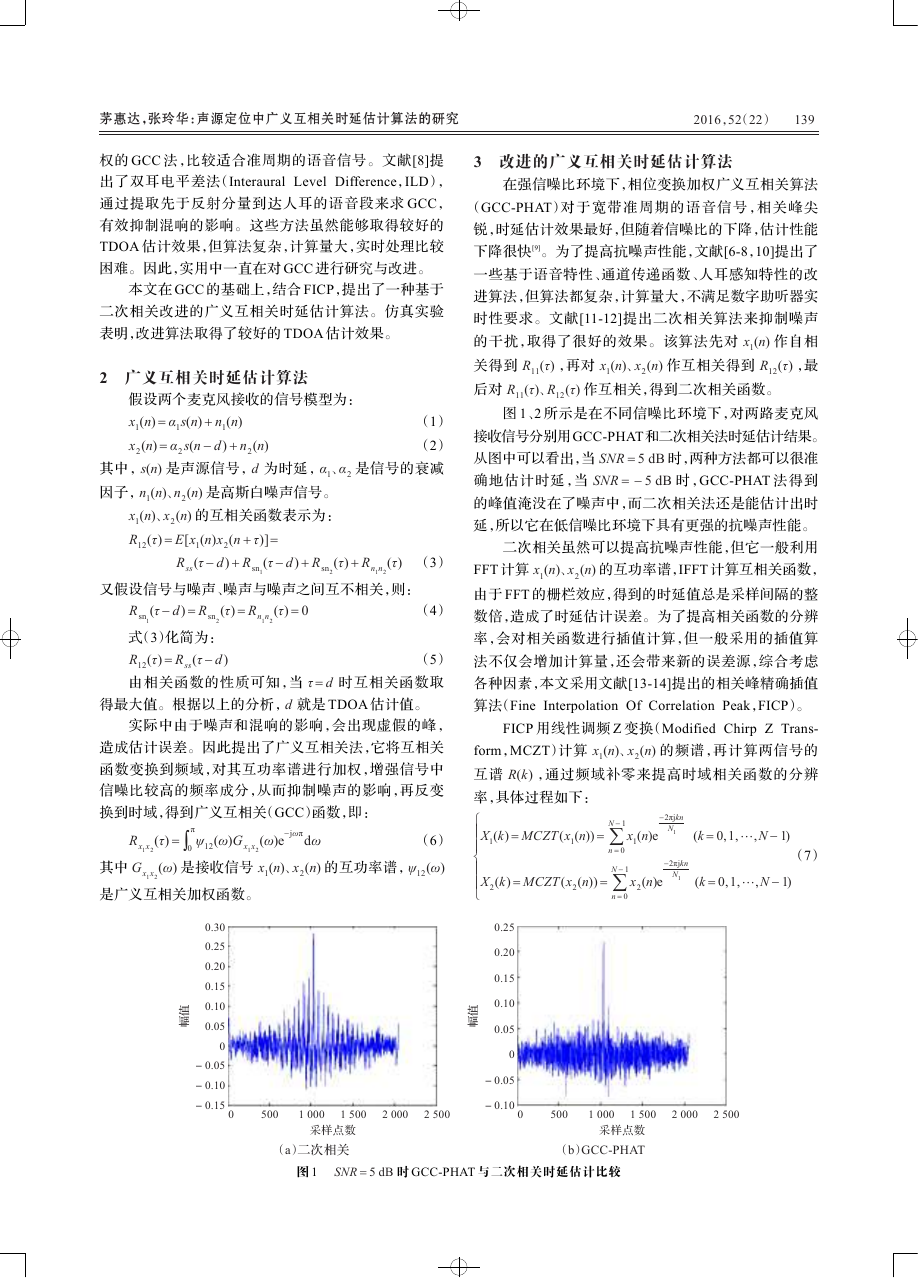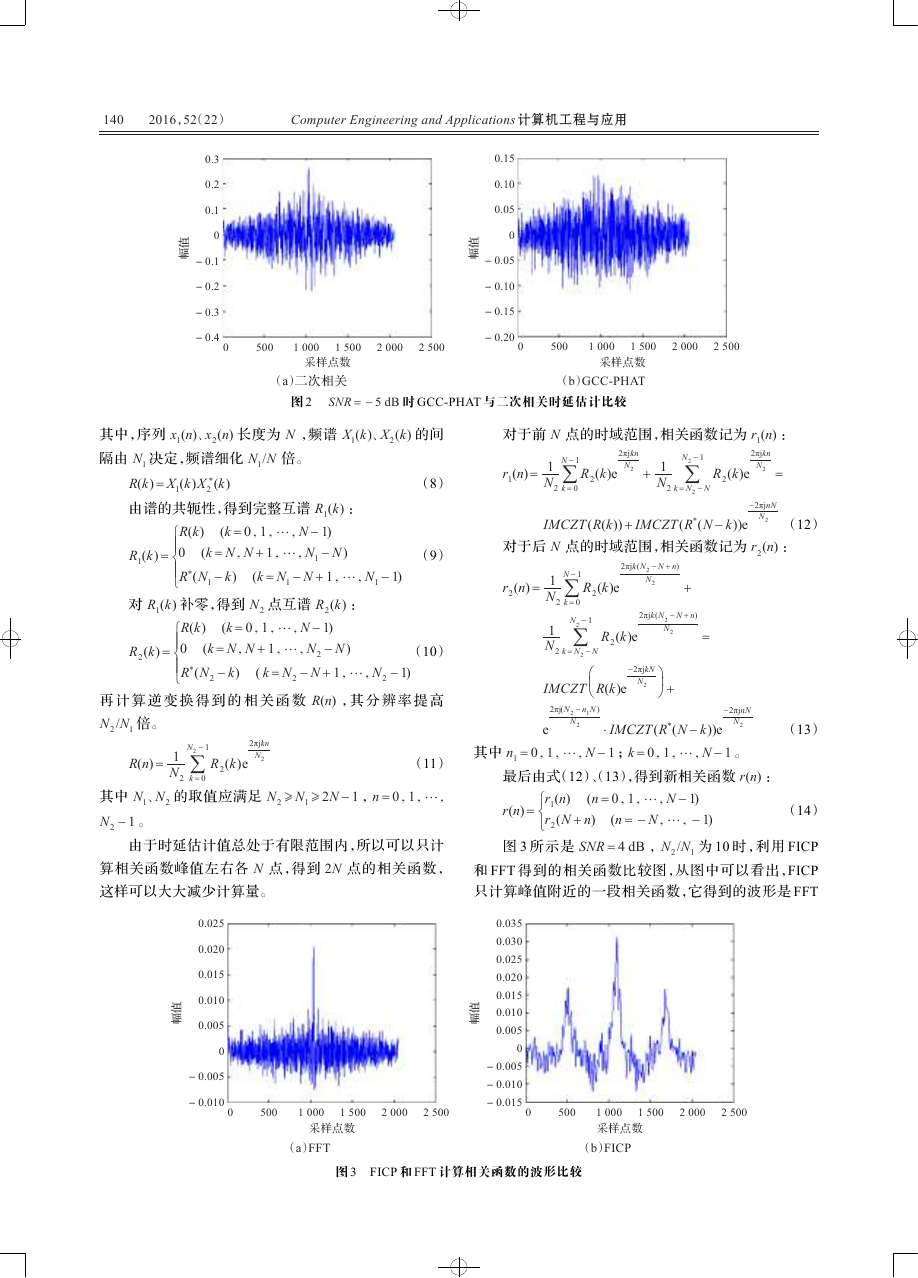 (n) 作互相关得到 R (τ) ，再对 x 1 11 (τ)、R (n)、x 2 11 12 图 1、2 所示是在不同信噪比环境下，对两路麦克风 接收信号分别用 GCC-PHAT和二次相关法时延估计结果。 从图中可以看出，当 SNR = 5 dB 时，两种方法都可以很准 确地估计时延，当 SNR = - 5 dB 时，GCC-PHAT 法得到 的峰值淹没在了噪声中，而二次相关法还是能估计出时 延，所以它在低信噪比环境下具有更强的抗噪声性能。 二次相关虽然可以提高抗噪声性能，但它一般利用 FFT 计算 x (n) 的互功率谱，IFFT 计算互相关函数， 1 由于 FFT 的栅栏效应，得到的时延值总是采样间隔的整 数倍，造成了时延估计误差。为了提高相关函数的分辨 率，会对相关函数进行插值计算，但一般采用的插值算 法不仅会增加计算量，还会带来新的误差源，综合考虑 各种因素，本文采用文献[13-14]提出的相关峰精确插值 算法（Fine Interpolation Of Correlation Peak，FICP）。 (n)、x 2 2 (n)、x FICP 用线性调频 Z 变换（Modified Chirp Z Trans- (n) 的频谱，再计算两信号的 form，MCZT）计算 x 1 互谱 R(k) ，通过频域补零来提高时域相关函数的分辨 率，具体过程如下： ì ï ï ïï í ï ï ïï î   (k = 0,1,,N - 1) (k) = MCZT (x 1   (k = 0,1,,N - 1) (k) = MCZT (x (n)) = å (n)) = å (n)e (n)e -2πjkn -2πjkn X 1 x 1 N - 1 N - 1 n = 0 X N 1 N 1 x 2 2 2 n = 0 （7） 0.30 0.25 0.20 0.15 0.10 0.05 0 －0.05 －0.10 －0.15 值 幅 0.25 0.20 0.15 0.10 0.05 0 －0.05 －0.10 值 幅 0 500 1 000 1 500 2 000 2 500 采样点数 （b）GCC-PHAT 0 500 1 000 1 500 2 000 2 500 采样点数 （a）二次相关 图 1 SNR = 5 dB 时 GCC-PHAT 与二次相关时延估计比较 

140 2016，52（22） Computer Engineering and Applications 计算机工程与应用 0.3 0.2 0.1 0 －0.1 －0.2 －0.3 －0.4 值 幅 0 500 1 000 1 500 2 000 2 500 采样点数 （a）二次相关 0.15 0.10 0.05 0 －0.05 －0.10 －0.15 －0.20 值 幅 0 500 1 000 1 500 2 000 2 500 采样点数 （b）GCC-PHAT 图 2 SNR = - 5 dB 时 GCC-PHAT 与二次相关时延估计比较 (n)、x (n) 长度为 N ，频谱 X 1 2 (k)、X 2 (k) 的间 对于前 N 点的时域范围，相关函数记为 r 1 (n) ： （8） r 1 (n) = 1 N 2 N - 1 å k = 0 2πjkn N (k)e R 2 2 + 1 N 2 N - 1 2 å k = N 2 - N 2πjkn N 2 = (k)e R 2 -2πjnN 其中，序列 x 1 隔由 N 1 决定，频谱细化 N 1 /N 倍。 (k) (k)X * 2 R(k) = X 1 由谱的共轭性，得到完整互谱 R 1 (k = 01N - 1) (k) ： R(k) ì ïï 0 í ïï î R*(N 1 R(k) ì ïï 0 í ïï î R*(N (k) = R 1 (k = NN + 1N 1 - N ) （9） - k) (k = N 1 - N + 1N 1 - 1) 对 R 1 (k) 补零，得到 N 点互谱 R (k) ： 2 2 (k = 01N - 1) (k) = R 2 (k = NN + 1N - N ) 2 （10） - k) 2 (  k = N 2 - N + 1N - 1) 2 再 计 算 逆 变 换 得 到 的 相 关 函 数 R(n) ，其 分 辨 率 提 高 N 倍。 /N 1 2 IMCZT (R(k)) + IMCZT (R*(N - k))e 对于后 N 点的时域范围，相关函数记为 r r 2 (n) = 1 N 2 N - 1 å k = 0 (k)e R 2 2πjk(N 2 N - N + n) 2 + N 2 （12） (n) ： 2 2πjk(N 2 N - N + n) 2 = (k)e R 2 1 N 2 N - 1 2 å k = N 2 - N æ èç IMCZT R(k)e -2πjkN N 2 ö ø÷ + - n 1 N ) 2πj(N e 2 N 2 × IMCZT (R*(N - k))e -2πjnN N 2 （13） 2πjkn N - 1 2 å R R(n) = 1 N 2 的取值应满足 N (k)e k = 0 N 2 2 其中 N 、N 1 - 1 。 N 2 2 （11） 其中 n 1 = 01N - 1 ；k = 01N - 1 。 最后由式（12）、（13），得到新相关函数 r(n) ：  N 1 2  2N - 1 ，n = 01 r(n) = (n)  (N + n) r ì 1 í r î 2 (n = 01N - 1) (n = - N - 1) （14） 由于时延估计值总处于有限范围内，所以可以只计 算相关函数峰值左右各 N 点，得到 2N 点的相关函数， 这样可以大大减少计算量。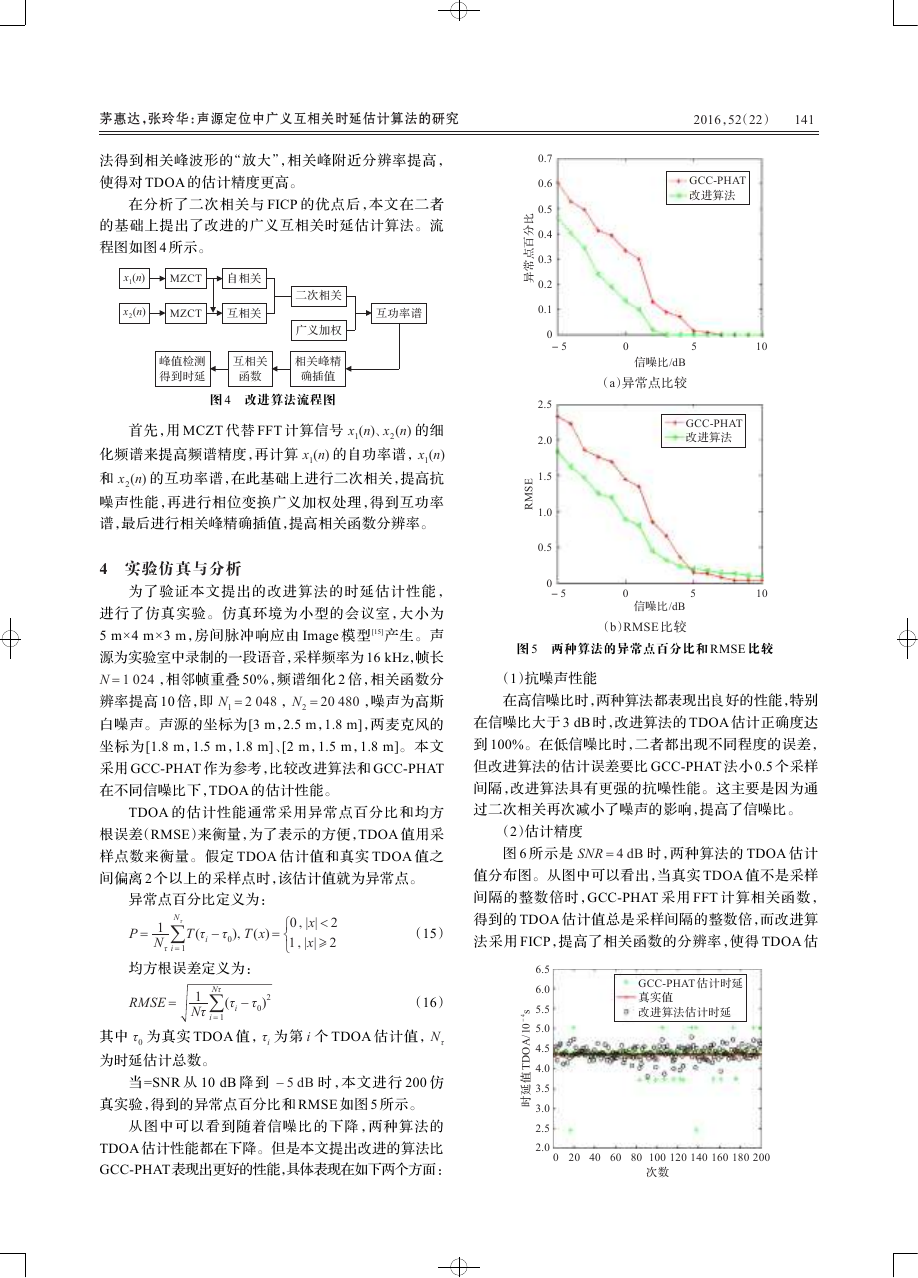 图 3 所示是 SNR = 4 dB ，N 为 10 时，利用 FICP 和 FFT 得到的相关函数比较图，从图中可以看出，FICP 只计算峰值附近的一段相关函数，它得到的波形是 FFT /N 1 2 0.025 0.020 0.015 0.010 0.005 0 －0.005 －0.010 值 幅 0 500 1 000 1 500 2 000 2 500 采样点数 （a）FFT 0.035 0.030 0.025 0.020 0.015 0.010 0.005 0 －0.005 －0.010 －0.015 值 幅 0 500 1 500 1 000 采样点数 2 000 2 500 （b）FICP 图 3 FICP 和 FFT 计算相关函数的波形比较 

茅惠达，张玲华：声源定位中广义互相关时延估计算法的研究 2016，52（22） 141 法得到相关峰波形的“放大”，相关峰附近分辨率提高， 使得对 TDOA 的估计精度更高。 在分析了二次相关与 FICP 的优点后，本文在二者 的基础上提出了改进的广义互相关时延估计算法。流 程图如图 4 所示。 (n) x 1 (n) x 2 MZCT 自相关 MZCT 互相关 二次相关 广义加权 互功率谱 峰值检测 得到时延 互相关 函数 相关峰精 确插值 图 4 改进算法流程图 (n)、x 首先，用 MCZT 代替 FFT 计算信号 x 1 (n) 的细 化频谱来提高频谱精度，再计算 x (n) 1 和 x (n) 的互功率谱，在此基础上进行二次相关，提高抗 噪声性能，再进行相位变换广义加权处理，得到互功率 谱，最后进行相关峰精确插值，提高相关函数分辨率。 (n) 的自功率谱，x 1 2 2 4 实验仿真与分析 为了验证本文提出的改进算法的时延估计性能， 进行了仿真实验。仿真环境为小型的会议室，大小为 5 m×4 m×3 m，房间脉冲响应由 Image 模型 [15]产生。声 源为实验室中录制的一段语音，采样频率为 16 kHz，帧长 N = 1 024 ，相邻帧重叠 50%，频谱细化 2 倍，相关函数分 = 20 480 ，噪声为高斯 辨率提高 10 倍，即 N 1 白噪声。声源的坐标为[3 m，2.5 m，1.8 m]，两麦克风的 坐标为[1.8 m，1.5 m，1.8 m]、[2 m，1.5 m，1.8 m]。本文 采用 GCC-PHAT 作为参考，比较改进算法和 GCC-PHAT 在不同信噪比下，TDOA 的估计性能。 = 2 048 ，N 2 TDOA 的估计性能通常采用异常点百分比和均方 根误差（RMSE）来衡量，为了表示的方便，TDOA 值用采 样点数来衡量。假定 TDOA 估计值和真实 TDOA 值之 间偏离 2 个以上的采样点时，该估计值就为异常点。 异常点百分比定义为： P = 1 N τ N å τ i = 1 T (τ i - τ 0 )T (x) = 0|x| < 2 ì í 1|x|  2 î 均方根误差定义为： RMSE = Nτ 1 Nτ å i = 1 (τ i - τ )2 0 （15） （16） 为真实 TDOA 值，τ 其中 τ 为时延估计总数。 0 为第 i 个 TDOA 估计值，N τ i 当=SNR 从 10 dB 降到 - 5 dB 时，本文进行 200 仿 真实验，得到的异常点百分比和 RMSE 如图 5 所示。 从图中可以看到随着信噪比的下降，两种算法的 TDOA 估计性能都在下降。但是本文提出改进的算法比 GCC-PHAT表现出更好的性能，具体表现在如下两个方面： GCC-PHAT 改进算法 0.7 0.6 0.5 0.4 0.3 0.2 0.1 比 分 百 点 常 异 0 －5 0 5 10 信噪比/dB （a）异常点比较 2.5 2.0 1.5 1.0 0.5 E S M R 0 －5 GCC-PHAT 改进算法 5 10 0 信噪比/dB （b）RMSE 比较 图 5 两种算法的异常点百分比和 RMSE 比较 （1）抗噪声性能 在高信噪比时，两种算法都表现出良好的性能，特别 在信噪比大于 3 dB 时，改进算法的 TDOA 估计正确度达 到 100%。在低信噪比时，二者都出现不同程度的误差， 但改进算法的估计误差要比 GCC-PHAT 法小 0.5 个采样 间隔，改进算法具有更强的抗噪性能。这主要是因为通 过二次相关再次减小了噪声的影响，提高了信噪比。 （2）估计精度 图 6 所示是 SNR = 4 dB 时，两种算法的 TDOA 估计 值分布图。从图中可以看出，当真实 TDOA 值不是采样 间隔的整数倍时，GCC-PHAT 采用 FFT 计算相关函数， 得到的 TDOA 估计值总是采样间隔的整数倍，而改进算 法采用 FICP，提高了相关函数的分辨率，使得 TDOA 估 6.5 6.0 5.5 5.0 4.5 4.0 3.5 3.0 2.5 2.0 s 4 － 0 1 / A O D T 值 延 时 GCC-PHAT 估计时延 真实值 改进算法估计时延 0 20 40 60 80 100 120 140 160 180 200 次数 

142 2016，52（22） Computer Engineering and Applications 计算机工程与应用 计值更加逼近真实值，具有更高的时延估计精度。 conditions[J].Signal Processing，1997，59：253-266. 5 结束语 TDOA 估计是数字助听器中实现声源定位的关键 一步，本文在 GCC 基础上，结合二次相关能有效抑制噪 声，FICP 能提高相关函数分辨率的优点，提出了改进算 法。仿真实验表明，无论在低信噪比，还是在高信噪比 环境下，改进算法都比参考方法具有更高的抗噪声性能 和 TDOA 估计精度。 参考文献： [1] Brandstein M.Microphone arrays：signal processing tech- niques and applications[M].New York：Springer，2001： 157-180. [2] 崔玮玮，曹志刚，魏建强.声源定位中的时延估计技术[J].数 据采集与处理，2007，22（1）：90-99. [3] Huang Y T，Benesty J，Elko G W.Passive acoustic source localization for video camera steering[C]//Proceedings of IEEE International Conference on Acoustic，Speech and Signal Processing，2000，2：909-912. [4] Nesta F，Omologo M.Generalized state coherence transform for multidimensional TDOA estimation of multiple sources[J]. IEEE Transactions on Speech and Audio Processing，2012， 20（1）：246-260. [5] Knapp C H，Carter G C.The generalized correlation method for estimation of time delay[J].IEEE Transactions on ASSP， 1976，24（4）：320-327. [6] Champagne B，Stephene A.A new cepstral prefiltering reverberant technique for estimating time delay under [7] Brandstein M S.A pitch-based approach to time delalay estimation of reverbeant speech[C]//Proceedings of IEEE Workshop on Application of Signal Processing to Audio and Acoustics，1997. [8] Costa M H，Naylor P A.ILD preservation in the multi- channel wiener for binaural hearing aid applica- tions[C]//Signal Processing Conference，2014 Proceedings of the 22nd European，2014：636-640. filter [9] Ali P，Mohammad A.Real time high accuracy 3-d PHAT- based sound source localization using a simple 4-micro- phone arrangement[J].IEEE Transactions on Systems Journal， 2012，6（3）：455-468. [10] Marinescu R，Buzo A.Fast accurate time delay estimation based on enhanced accumulated cross-power spectrum phase[C]//Signal Processing Conference，2013 Proceedings of the 21st European，2013：1-5. [11] 唐娟，行鸿彦.基于二次相关的时延估计算法[J].计算机工 程，2007，33（21）：265-267. [12] Jin Liunian.Research on time delay estimation based on second correlation[J].Electronic Information Warfare Tech- nology，2011，26（1）：39-42. [13] 杨亦春，马池州.相关峰细化的精确时延估计快速算法研 究[J].声学学报，2003，28（2）：160-163． [14] 韩洁，吴长奇.相关峰插值的二次相关锐化时延估计方法[J]. 信号处理，2014，30（10）：1241-1244. [15] Allen J B，Berkley D A.Image method for efficiently simulating small-room acoustics[J].Journal of Acoustical Society of America，1979，65（4）：943-950. （上接 112 页） [8] Nadkarni S，Shenoy P P.A causal mapping approach to constructing Bayesian networks[J].Decision Support Sys- tems，2004，38（2）：259-281. [9] Cressie N，Calder C A，Clark J S，et al.Accounting for uncertainty in ecological analysis：the strengths and limi- tations of hierarchical statistical modeling[J].Ecological Applications：A Publication of the Ecological Society of America，2009，19（3）：553-570. [10] Mccarthy M A，Masters P.Profiting from prior informa- tion in Bayesian analyses of ecological data[J].J Appl Ecol，2005，42（6）：1012-1019. to [11] Nielsen S H，Nielsen T D.Adapting Bayes network structures domains[J].International Journal of Approximate Reasoning，2008，49（2）：379-397. [12] Bressan G M，Oliveira V A，Hruschka J R E R，et al. Using Bayesian networks with rule extraction to infer non-stationary the risk of weed infestation in a corn-crop[J].Engineering Intelligence，2009，22（4/5）： Applications of Artificial 579-592. [13] Sinha A P，Zhao H.Incorporating domain knowledge into data mining classifiers：An application in indirect lending[J]. Decision Support Systems，2008，46（1）：287-299. [14] Tversky A，Kahneman D.Advances in prospect theory： Cumulative representation of uncertainty[J].Journal of Risk and Uncertainty，1992. [15] Saaty T L.Rank from comparisons and from ratings in the analytic hierarchy/network processes time dependent decision-making；dynamic priorities in the AHP/ANP： Generalizing from points to functions and from real to complex variables[J].European Journal of Operational Research，2006，168（2）：557-570. [16] Moran A.Thinking in action：Some insights from cogni- tive sport psychology[J].Thinking Skills and Creativity， 2012，7（2）：85-92.