2021年中考数学压轴题精选含答案.doc-资料库

第1页 / 共68页

第2页 / 共68页

第3页 / 共68页

第4页 / 共68页

第5页 / 共68页

第6页 / 共68页

第7页 / 共68页

第8页 / 共68页

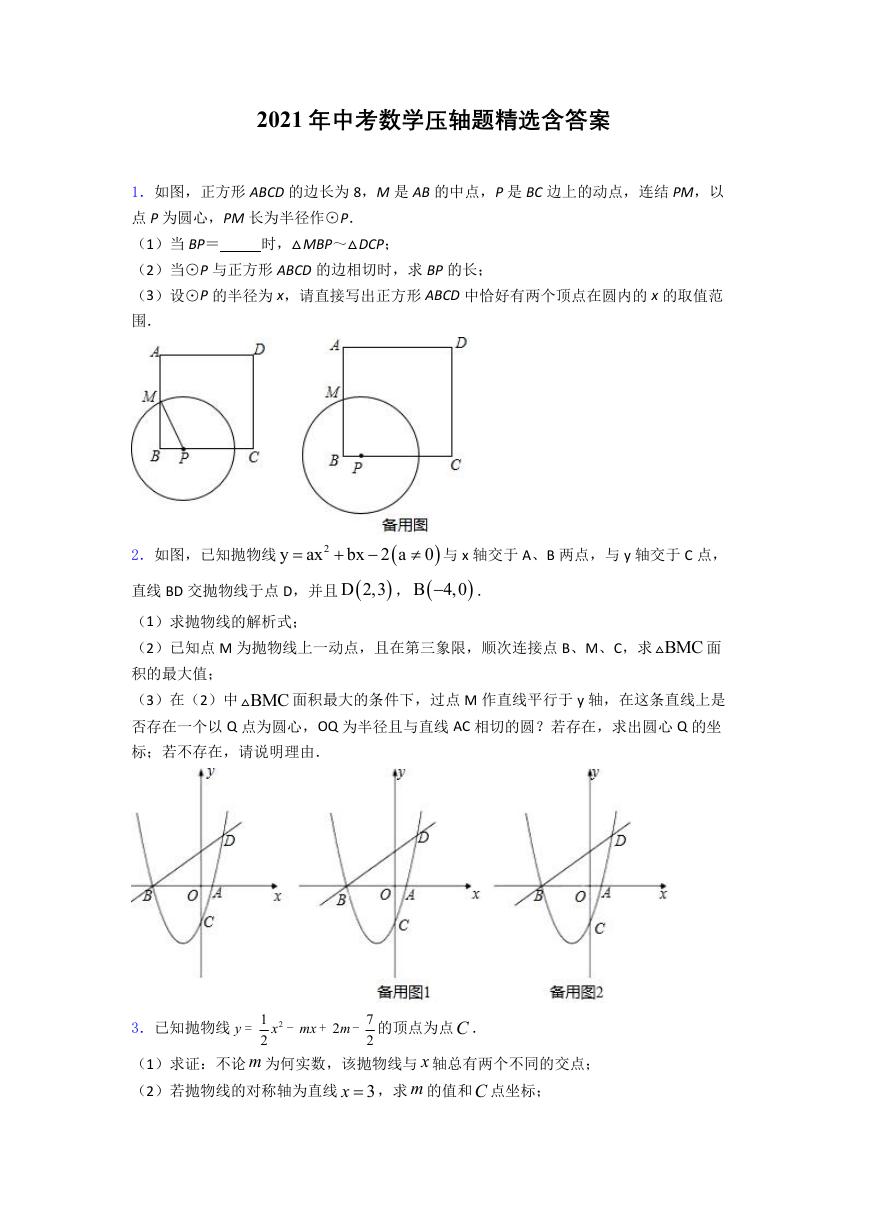
2021 年中考数学压轴题精选含答案 1．如图，正方形 ABCD 的边长为 8，M 是 AB 的中点，P 是 BC 边上的动点，连结 PM，以点 P 为圆心，PM 长为半径作⊙P．（1）当 BP＝（2）当⊙P 与正方形 ABCD 的边相切时，求 BP 的长；（3）设⊙P 的半径为 x，请直接写出正方形 ABCD 中恰好有两个顶点在圆内的 x 的取值范围．时，△MBP～△DCP；   面  ． y ax  2  bx 2 a 0   与 x 轴交于 A、B 两点，与 y 轴交于 C 点， D 2,3 ，   B 4,0 2．如图，已知抛物线直线 BD 交抛物线于点 D，并且  （1）求抛物线的解析式；（2）已知点 M 为抛物线上一动点，且在第三象限，顺次连接点 B、M、C，求 BMC 积的最大值；（3）在（2）中 BMC 面积最大的条件下，过点 M 作直线平行于 y 轴，在这条直线上是否存在一个以 Q 点为圆心，OQ 为半径且与直线 AC 相切的圆？若存在，求出圆心 Q 的坐标；若不存在，请说明理由．   3．已知抛物线 y = 21 x 2 - mx + 2 m - 的顶点为点C ． 7 2 （1）求证：不论 m 为何实数，该抛物线与 x 轴总有两个不同的交点；（2）若抛物线的对称轴为直线 3x  ，求 m 的值和C 点坐标；

y x  与（2）中的抛物线并于 A B、两点，并与它的对称轴交于点 D ，、、、为顶 k 交直线 AB 于点 M ，交抛物线于点 N ．求当 k 为何值时，以 C D M N 1 （3）如图，直线直线 x 点的四边形为平行四边形． 4．如图，在四边形 ABCD 中，∠B=90°，AD//BC，AD=16，BC=21，CD=13．（1）求直线 AD 和 BC 之间的距离；（2）动点 P 从点 B 出发，沿射线 BC 以每秒 2 个单位长度的速度运动，动点 Q 从点 A 出发，在线段 AD 上以每秒 1 个单位长度的速度运动，点 P、Q 同时出发，当点 Q 运动到点 D 时，两点同时停止运动，设运动时间为 t 秒．试求当 t 为何值时，以 P、Q、D、C 为顶点的四边形为平行四边形？（3）在（2）的条件下，是否存在点 P，使△PQD 为等腰三角形？若存在，请直接写出相应的 t 值，若不存在，请说明理由． 60  ，过点 A 作 AE BC ，垂足为 E ，  ABC ，垂足为 F ． 5．如图，在菱形 ABCD 中， AB a= ， AF CD （1）连接 EF ，用等式表示线段 EF 与 EC 的数量关系，并说明理由；（2）连接 BF ，过点 A 作 AK （3）延长线段CB 到G ，延长线段 DC 到 H ，且 BG CH ①判断 AGH 的形状，并说明理由； BF ，垂足为 K ，求 BK 的长(用含 a 的代数式表示)；，连接 AG ，GH ， AH ． ②若 a  2, S  ADH  1 2 (3  3) ，求sin GAB 的值． 6．问题提出（1）如图①，在 ABC  中， AB  4 2, AC   6, BAC  135  ，求 ABC  的面积．

问题探究（2）如图②，半圆O 的直径  2 CD BD AB  ，C 是半圆 AB 的中点，点 D 在 BC 上，且 10 ，点 P 是 AB 上的动点，试求 PC PD 的最小值．问题解决（3）如图③，扇形 AOB 的半径为 20, 在边OB 上选点 F ，求 PE EF FP   的长度的最小值． AOB  45  在 AB 选点 P ，在边OA 上选点 E ， 7．如图，在 ABC 中， AB  ， 14 B  45  ， tan A  ，点 D 为 AB 中点．动点 P 从 4 3 点 D 出发，沿 DA 方向以每秒1个单位长度的速度向终点 A 运动，点 P 关于点 D 对称点为点Q ，以 PQ 为边向上作正方形 PQMN ．设点 P 的运动时间为 t 秒．内部时，求 S 关于的分为面积相等的两部分时，直接写出重叠部分面积为 S ，当点 N 在 ABC （1）当t  _______秒时，点 N 落在 AC 边上．（2）设正方形 PQMN 与 ABC t 的函数关系式．（3）当正方形 PQMN 的对角线所在直线将 ABC t 的值． 8．对于平面直角坐标系 xOy 中的图形 W1 和图形 W2．给出如下定义：在图形 W1 上存在两点 A，B（点 A，B 可以重合），在图形 W2 上存在两点 M，N，（点 M 于点 N 可以重合）使得 AM=2BN，则称图形 W1 和图形 W2 满足限距关系 (1)如图 1，点 C(1，0)，D(-1，0)，E(0， 3 )，点 P 在线段 DE 上运动(点 P 可以与点 D，E 重合)，连接 OP，CP． ①线段 OP 的最小值为_______，最大值为_______；线段 CP 的取值范直范围是_____； ②在点 O，点 C 中，点____________与线段 DE 满足限距关系；

y  3 x b  (b>0)与 x 轴、y 轴分别交于点 F，G．若线段 (2)如图 2，⊙O 的半径为 1，直线 FG 与⊙O 满足限距关系，求 b 的取值范围； (3)⊙O 的半径为 r(r>0)，点 H，K 是⊙O 上的两个点，分别以 H，K 为圆心，1 为半径作圆得到⊙H 和K，若对于任意点 H，K，⊙H 和⊙K 都满足限距关系，直接写出 r 的取值范围． 9．如图，在平面直角坐标系中，点 (1,2) A 轴正半轴于点C ，连结 AO ， AB ．（1）求点C 的坐标；（2）求直线 AB 的表达式； 0) y （3）设抛物线 AO ，求抛物线表达式；  分别交边 BA ， BA 延长线于点 D ， E ．， (5,0)  交 x 2 ( ax a 2 ( ax a ，抛物线  2 ax 0) y  2 ax B   ①若 AE 2 与 BOA△ 相似，则 a 的值为 ②若 CDB△ ．（直接写出答案） 10．如图，射线 AM 上有一点 B，AB＝6．点 C 是射线 AM 上异于 B 的一点，过 C 作 CD⊥AM，且 CD＝ 4 3 AC．过 D 点作 DE⊥AD，交射线 AM 于 E. 在射线 CD 取点 F，使得 CF ＝CB，连接 AF 并延长，交 DE 于点 G．设 AC＝3x．（1）当 C 在 B 点右侧时，求 AD、DF 的长．(用关于 x 的代数式表示) （2）当 x 为何值时，△AFD 是等腰三角形．（3）若将△DFG 沿 FG 翻折，恰使点 D 对应点 'D 落在射线 AM 上，连接 'FD ， 'GD ．此时 x 的值为（直接写出答案）

8 cm ， BC cm 6 16 AB  ，，动点Q 从点 D 开始沿 DA 边匀速运动，运动速度为1 /cm s ，动点 P 从点 A /cm s ．点 P 和点Q 同时出发，O 为四边形 ABCD 11．已知：如图，四边形 ABCD ， AB DC ，CB AB ， CD cm 开始沿 AB 边匀速运动，运动速度为 2 的对角线的交点，连接 PO 并延长交 CD 于 M ，连接 QM ．设运动的时间为   8t  ． 0 （1）当t 为何值时， PQ BD ？（2）设五边形QPBCM 的面积为  S cm ，求 S 与t 之间的函数关系式； t s ， 2 （3）在运动过程中，是否存在某一时刻t ，使 PQM 的面积等于五边形面积的 11 15 ？若存在，求出t 的值；若不存在，请说明理由；（4）在运动过程中，是否存在某一时刻t ，使点Q 在 MP 的垂直平分线上？若存在，求出 t 的值；若不存在，请说明理由． 12．如图 1，平面直角坐标系 xoy 中，A(－4，3)，反比例函数 y  k x ( k  的图象分别交 0) 矩形 ABOC 的两边 AC，BC 于 E，F（E，F 不与 A 重合），沿着 EF 将矩形 ABOC 折叠使 A， D 重合．（1）①如图 2，当点 D 恰好在矩形 ABOC 的对角线 BC 上时，求 CE 的长；

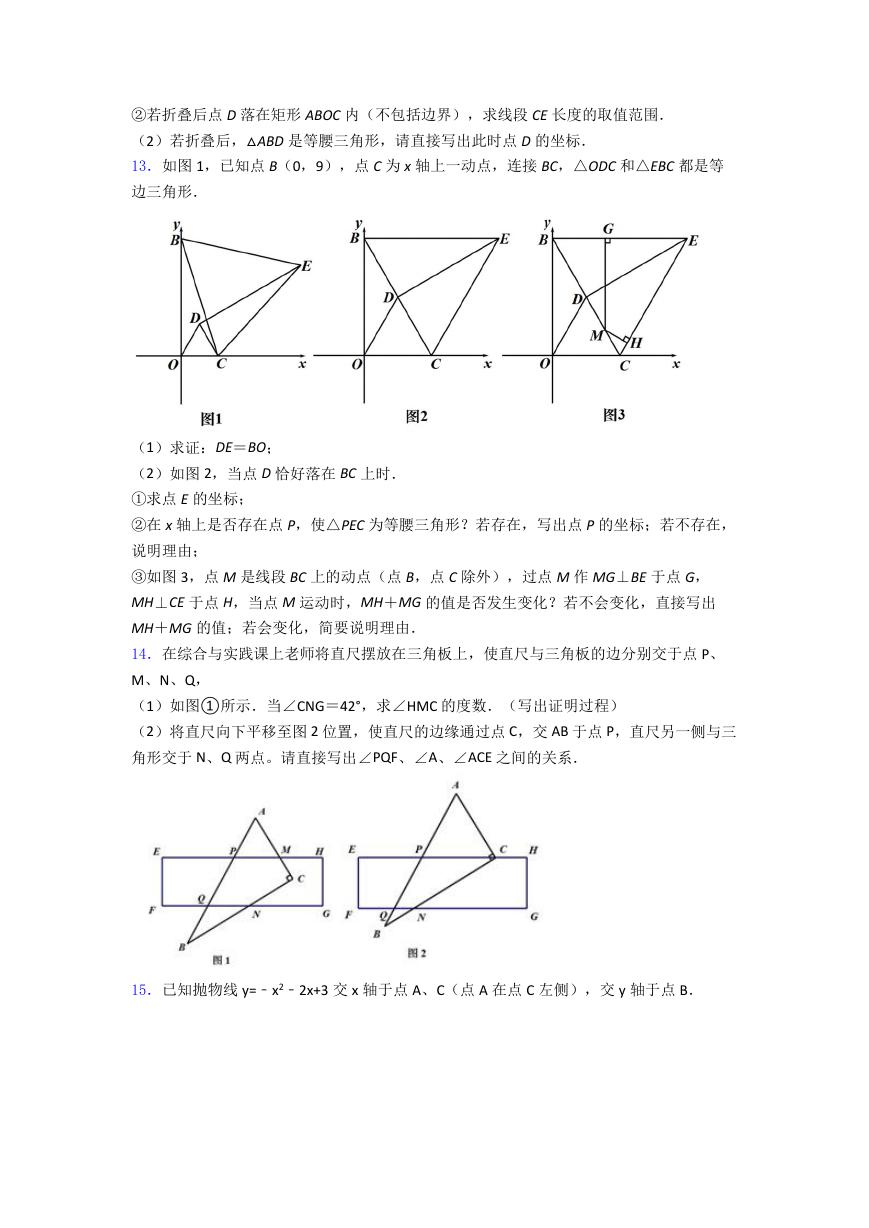
②若折叠后点 D 落在矩形 ABOC 内（不包括边界），求线段 CE 长度的取值范围．（2）若折叠后，△ABD 是等腰三角形，请直接写出此时点 D 的坐标． 13．如图 1，已知点 B（0，9），点 C 为 x 轴上一动点，连接 BC，△ODC 和△EBC 都是等边三角形．（1）求证：DE＝BO；（2）如图 2，当点 D 恰好落在 BC 上时． ①求点 E 的坐标； ②在 x 轴上是否存在点 P，使△PEC 为等腰三角形？若存在，写出点 P 的坐标；若不存在，说明理由； ③如图 3，点 M 是线段 BC 上的动点（点 B，点 C 除外），过点 M 作 MG⊥BE 于点 G， MH⊥CE 于点 H，当点 M 运动时，MH＋MG 的值是否发生变化？若不会变化，直接写出 MH＋MG 的值；若会变化，简要说明理由． 14．在综合与实践课上老师将直尺摆放在三角板上，使直尺与三角板的边分别交于点 P、 M、N、Q，（1）如图①所示．当∠CNG＝42°，求∠HMC 的度数．（写出证明过程）（2）将直尺向下平移至图 2 位置，使直尺的边缘通过点 C，交 AB 于点 P，直尺另一侧与三角形交于 N、Q 两点。请直接写出∠PQF、∠A、∠ACE 之间的关系． 15．已知抛物线 y=﹣x2﹣2x+3 交 x 轴于点 A、C（点 A 在点 C 左侧），交 y 轴于点 B．

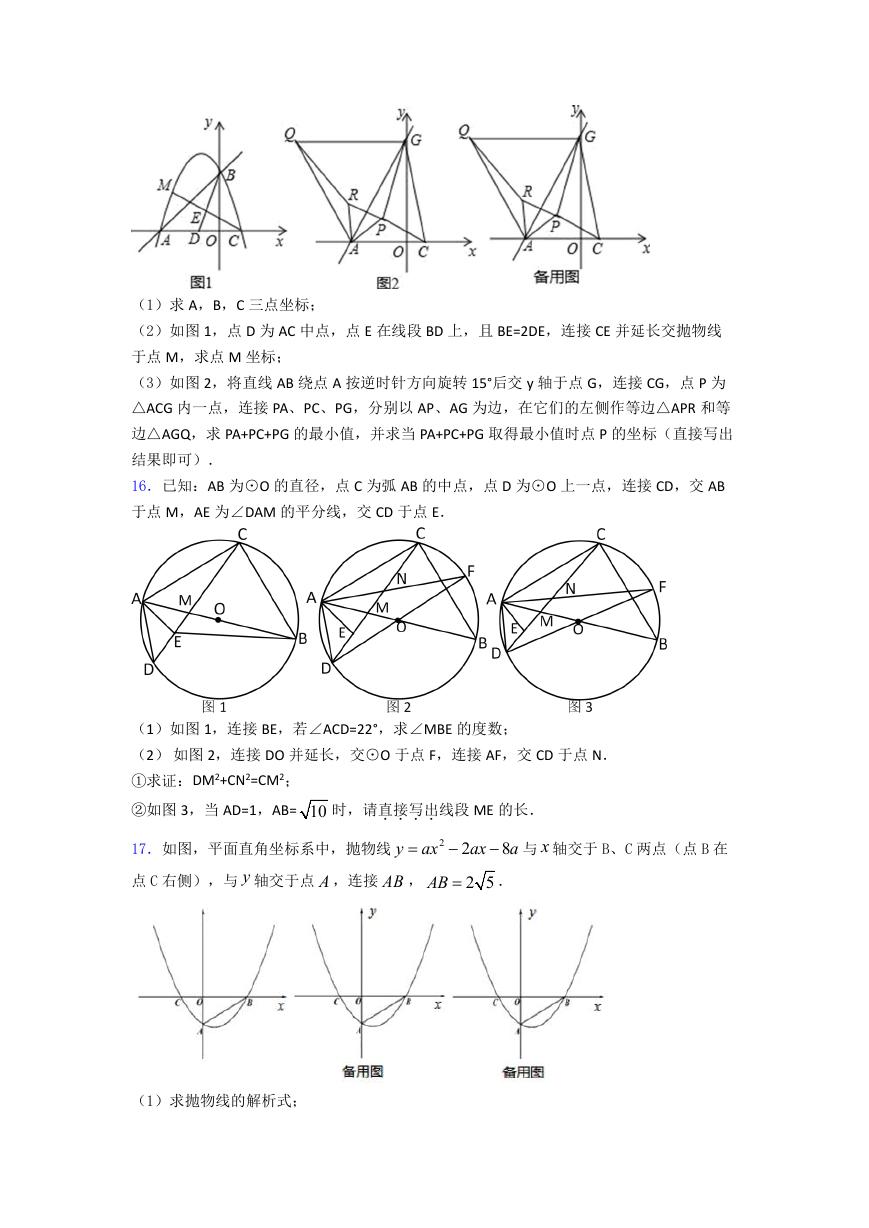
（1）求 A，B，C 三点坐标；（2）如图 1，点 D 为 AC 中点，点 E 在线段 BD 上，且 BE=2DE，连接 CE 并延长交抛物线于点 M，求点 M 坐标；（3）如图 2，将直线 AB 绕点 A 按逆时针方向旋转 15°后交 y 轴于点 G，连接 CG，点 P 为 △ACG 内一点，连接 PA、PC、PG，分别以 AP、AG 为边，在它们的左侧作等边△APR 和等边△AGQ，求 PA+PC+PG 的最小值，并求当 PA+PC+PG 取得最小值时点 P 的坐标（直接写出结果即可）． 16．已知：AB 为⊙O 的直径，点 C 为弧 AB 的中点，点 D 为⊙O 上一点，连接 CD，交 AB 于点 M，AE 为∠DAM 的平分线，交 CD 于点 E．（1）如图 1，连接 BE，若∠ACD=22°，求∠MBE 的度数；（2）如图 2，连接 DO 并延长，交⊙O 于点 F，连接 AF，交 CD 于点 N． ①求证：DM2+CN2=CM2； ②如图 3，当 AD=1，AB= 10 时，请直接写出．．．．线段 ME 的长．  17．如图，平面直角坐标系中，抛物线点 C 右侧），与 y 轴交于点 A ，连接 AB ， y  与 x 轴交于 B、C 两点（点 B 在 8 a 2 2 ax  AB  ax 2 5 ．（1）求抛物线的解析式；

的面积为 S ，求 S 与t 的函数（2）点 P 在第二象限的抛物线上，连接 PB 交 y 轴于 D，取 PB 的中点 E，过点 E 作 EH x 轴于点 H，连接 DH，设点 P 的横坐标为 t . ODH 关系式（不要求写出自变量 t 的取值范围）； y 轴于 F，连接 CP、CD，CP CD （3）在（2）的条件下，作 PF 点，连接 BS 交 y 轴于点T ，连接 BF 并延长交抛物线于点 R . SBC 射线 CS 上取点 Q.连接 QF，QF RF 18．定义：将函数 l 的图象绕点 P（m，0）旋转 180°，得到新的函数 l'的图象，我们称函数 l'是函数关于点 P 的相关函数．例如：当 m＝1 时，函数 y＝（x+1）2+5 关于点 P（1，0）的相关函数为 y＝﹣（x﹣3）2﹣ 5．（1）当 m＝0 时 ①一次函数 y＝x﹣1 关于点 P 的相关函数为  ，求直线TQ 的解析式．，点 S 为 PF 上一   ，在  FBO 45 ； 9 8 ）在二次函数 y＝﹣ax2﹣ax+1（a≠0）关于点 P 的相关函数的图象上，求，﹣ ②点（ 1 2 a 的值．（2）函数 y＝（x﹣1）2+2 关于点 P 的相关函数 y＝﹣（x+3）2﹣2，则 m＝；（3）当 m﹣1≤x≤m+2 时，函数 y＝x2﹣mx﹣ 1 2 m2 关于点 P（m，0）的相关函数的最大值为 6，求 m 的值． 19．如图，在▱ABCD 中，对角线 AC⊥BC，∠BAC＝30°，BC＝2 3 ，在 AB 边的下方作射线 AG，使得∠BAG＝30°，E 为线段 DC 上一个动点，在射线 AG 上取一点 P，连接 BP，使得∠EBP＝60°，连接 EP 交 AC 于点 F，在点 E 的运动过程中，当∠BPE＝60°时，则 AF＝ _____． 20．如图，在平面直角坐标系 xOy 中，已知 Rt ABC x 轴上，且点 A 的坐标为 物线  过 D ，C ， E 三点． 12 9,0 ax bx   y 2 ，斜边 AB 在，点 D 是 AC 的中点，点 E 是 BC 边上的一个动点，抛的直角顶点  C 0,12 

资料库

2021年中考数学压轴题精选含答案.doc

相关推荐

中考

热门标签

最新资料