第1页 / 共51页
第2页 / 共51页
第3页 / 共51页
第4页 / 共51页
第5页 / 共51页
第6页 / 共51页
第7页 / 共51页
第8页 / 共51页
计算机图形学实验报告.doc
2、梁友栋—Barsky裁剪算法描述
1、Bezier曲线的定义：
,
2、三次Bezier曲线的参数表示：
南昌大学实验报告
1、Bezier曲面的定义与生成
2、B样条曲面的定义、生成算法
南昌大学实验报告
二、实验目的
三、实验内容
四、实验要求
六、实验步骤
七、实验报告要求
#include "stdafx.h"
#include "resource.h"
#include "math.h"
#define MAX_LOADSTRING 100
#define KA 0.5 ////物体表面对泛光的反射系数
#define IA 0.02 ////入射的泛光光强
#define KD 0.5 ////漫反射系数
#define Il 0.8 ////入射的光强
#define IR 150 ////入射的红光光强
#define IG 150 ////入射的绿光光强
#define IB 150 ////入射的蓝光光强
#define KS 0.82 ////镜面反射系数
double xc=0,yc=-1500,zc=-3000;////////////设定视点方向
double lx=0,ly=300,lz=-200;////////////设定光源方向
///////////////////////////////////////////
double Cw(double w,double A[][3],int k,int j){
double tem;
tem=(1-w)*(1-w)*(1-w)*A[k][j]+3*w*(1-w)*(1-w)*A[k
return tem;
}
double Suw(double u,double w,double A[][3],int k,i
double tem;
tem=(1-u)*(1-u)*(1-u)*Cw(w,A,k,j)+3*u*(1-u)*(1-u)
return tem;
}
double daou(double u,double w,double A[][3],int k,
double tem;
tem=(6*u-3*u*u-3)*Cw(w,A,k,j)+(9*u*u-12*u+3)*Cw(w
return tem;
}
double daowc(double u,double A[][3],int k,int j){
double tem;
tem=(1-u)*(1-u)*(1-u)*A[k][j]+3*u*(1-u)*(1-u)*A[k
return tem;
}
double daow(double w,double u,double A[][3],int k,
double tem;
tem=(6*w-3*w*w-3)*daowc(u,A,k,j)+(9*w*w-12*w+3)*d
return tem;
}
/////////////////////////////////////////////
LRESULT CALLBACK WndProc(HWND hWnd, UINT message,
{
int k=0,m=1000;
double P[18][2]={{1.4000,2.2500},{1.3375,2.38125}
{0.2,2.55},{0.4,2.4},{1.3,2.4},{1.3,2.25},{0.0,3.
////////{0.0,3.0},{0.8,3.0},{0.0,2.7},{0.2,2.55},{
double A[56][3]={{1.7,1.27,0.0},{1.7,1.27,0.66},{
{2.6,1.275,0.0},{2.6,1.275,0.66},{3.1,0.675,0.66}
{2.3,1.95,0.0},{2.3,1.95,0.25},{2.4,1.875,0.25},{
{2.7,2.25,0.0},{2.7,2.25,0.25},{3.3,2.2,0.25},{3.
{2.8,2.325,0.0},{2.8,2.325,0.25},{3.525,2.34375,0
{2.9,2.325,0.0},{2.9,2.325,0.15},{3.4,2.3625,0.15
{2.8,2.25,0.0},{2.8,2.25,0.15},{3.2,2.25,0.15},{3
{1.6,1.875,0.0},{1.6,1.875,0.30},{1.5,2.1,0.30},{
{2.3,1.875,0.0},{2.3,1.875,0.30},{2.5,2.1,0.30},{
{2.7,1.875,0.0},{2.7,1.875,0.30},{3.0,2.1,0.30},{
{2.7,1.65,0.0},{2.7,1.65,0.30},{3.0,1.65,0.30},{3
{2.7,1.425,0.0},{2.7,1.425,0.30},{3.0,1.20,0.30},
{2.5,0.975,0.0},{2.5,0.975,0.30},{2.65,0.7875,0.3
{2.0,0.75,0.0},{2.0,0.75,0.30},{1.90,0.45,0.30},{
//粉色RGB（255,191,192）紫色RGB（200,88,100）
double X,Y,Z,t,q,R,a,u,w,j,i;
double XT,YT,ZT,XQ,YQ,ZQ,NX,NY,NZ;
double RX,RY,RZ,XC,YC,ZC,LX,LY,LZ,l,arfa,thta,bat
double I;////三色的光强
//HPEN hpen=CreatePen(PS_SOLID,1,RGB(255,191,192)
int wmId, wmEvent;
PAINTSTRUCT ps;
HDC hdc;
TCHAR szHello[MAX_LOADSTRING];
LoadString(hInst, IDS_HELLO, szHello, MAX_LOADSTR
switch (message)
{
case WM_COMMAND:
wmId = LOWORD(wParam);
wmEvent = HIWORD(wParam);
// Parse the menu selections:
switch (wmId)
{
case IDM_ABOUT:
DialogBox(hInst, (LPCTSTR)IDD_ABOUTBOX, hWn
break;
case IDM_EXIT:
DestroyWindow(hWnd);
break;
default:
return DefWindowProc(hWnd, message, wParam,
}
break;
case WM_PAINT:
hdc = BeginPaint(hWnd, &ps);
// TODO: Add any drawing code here...
RECT rt;
GetClientRect(hWnd, &rt);
//SelectObject(hdc,hpen);
{
while(k<=14){
for(j=0.0;j<=m;j++){
t=j/m;
R=(1-t)*(1-t)*(1-t)*P[k][0]+3*t*(1-t)*(1-t)*
for(a=0.0;a<=360;a++){
q=2*3.1415926*a/36
X=R*cos(q);
Z=R*sin(q);
Y=(1-t)*(1-t)*(1-t)*P[k][1]+3*t*(1-t)*(1-t
/////////////////////////消隐开始//////////////
XT=(6*t-3*t*t-3)*P[k][0]+(9*t*t-12*t+3)*P[
ZT=XT;
XT=XT*cos(q);
YT=(6*t-3*t*t-3)*P[k][1]+(9*t*t-12*t+3)*P[
ZT=ZT*sin(q);
XQ=R*(-sin(q));
YQ=0;
ZQ=R*cos(q);
NX=YT*ZQ-ZT*YQ;///
NY=ZT*XQ-XT*ZQ;
NZ=XT*YQ-YT*XQ;
l=sqrt(NX*NX+NY*NY+NZ*NZ);
NX=NX/l;
NY=NY/l;
NZ=NZ/l;
XC=xc-X;////////////////视线方向
YC=yc-Y;
ZC=zc-Z;
l=sqrt(XC*XC+YC*YC+ZC*ZC);
XC=XC/l;
YC=YC/l;
ZC=ZC/l;
LX=lx-X;////////////////光线方向
LY=ly-Y;
LZ=lz-Z;
l=sqrt(LX*LX+LY*LY+LZ*LZ);
LX=LX/l;
LY=LY/l;
LZ=LZ/l;
arfa=NX*XC+NY*YC+NZ*ZC;//////////////////法向
thta=LX*NX+LY*NY+LZ*NZ;//////////////////法向
NX=NX*LX*thta;
NY=NY*LY*thta;
NZ=NZ*LZ*thta;
RX=2*NX-LX;////////////////反射方向
RY=2*NY-LY;
RZ=2*NZ-LZ;
l=sqrt(RX*RX+RY*RY+RZ*RZ);
RX=RX/l;
RY=RY/l;
RZ=RZ/l;
bata=RX*XC+RY*YC+RZ*ZC;///////////////视线与反射
if(arfa>=0){
X=(xc*Z-X*zc)/(Z-zc);
Y=(yc*Z-Y*zc)/(Z-zc);
I=IR*KA+KD*Il*
SetPixel(hdc,400+int(80*X),400+int(80*(-Y
//SetPixel(hdc,400+int(80*X),400+int(80*(
}
}
}
if(k==6||k==10) k=k+4;
elsek+=3;
}
/////////////画立体壶嘴和把手/////////////////////////////
k=0;
while(k<=40){
for(i=0.0;i<=500;i++){
u=i/500;
for(j=0.0;j<=500;j++){
w=j/500;
X=Suw(u,w,A,k,0);
Y=Suw(u,w,A,k,1);
Z=Suw(u,w,A,k,2);
//////////////////////////////////////////////////
XT=daou(u,w,A,k,0);
YT=daou(u,w,A,k,1);
ZT=daou(u,w,A,k,2);
XQ=daow(w,u,A,k,0);
YQ=daow(w,u,A,k,1);
ZQ=daow(w,u,A,k,2);
NX=YT*ZQ-ZT*YQ;//////////法向量
NY=ZT*XQ-XT*ZQ;
NZ=XT*YQ-YT*XQ;
l=sqrt(NX*NX+NY*NY+NZ*NZ);
NX=NX/l;
NY=NY/l;
NZ=NZ/l;
XC=xc-X;////////////////视线方向
YC=yc-Y;
ZC=zc-Z;
l=sqrt(XC*XC+YC*YC+ZC*ZC);
XC=XC/l;
YC=YC/l;
ZC=ZC/l;
LX=lx-X;////////////////光线方向
LY=ly-Y;
LZ=lz-Z;
l=sqrt(LX*LX+LY*LY+LZ*LZ);
LX=LX/l;
LY=LY/l;
LZ=LZ/l;
arfa=NX*XC+NY*YC+NZ*ZC;//////////////////法向
thta=LX*NX+LY*NY+LZ*NZ;//////////////////法向
NX=NX*LX*thta;
NY=NY*LY*thta;
NZ=NZ*LZ*thta;
RX=2*NX-LX;
RY=2*NY-LY;
RZ=2*NZ-LZ;
l=sqrt(RX*RX+RY*RY+RZ*RZ);
RX=RX/l;
RY=RY/l;
RZ=RZ/l;
bata=RX*XC+RY*YC+RZ*ZC;///////////////视线与反射
////////////////////////////////////消隐/////
//if(arfa>=0){
X=(xc*Z-X*zc)/(Z-zc);
Y=(yc*Z-Y*zc)/(Z-zc);
if(k==28||k==40) X=-X;
I=IR*KA+KD*Il*
SetPixel(hdc,400+int(80*X),400+int(80*(-Y
//SetPixel(hdc,400+int(80*X),400+int(80*(
//}
}
}
if(k==12) k+=16;
else k+=12;
}
}
//DrawText(hdc, szHello, strlen(szHello), &rt,
EndPaint(hWnd, &ps);
break;
case WM_DESTROY:
PostQuitMessage(0);
break;
default:
return DefWindowProc(hWnd, message, wParam, lPa
}
return 0;
}
// Mesage handler for about box.
LRESULT CALLBACK About(HWND hDlg, UINT message, WP
{
switch (message)
{
case WM_INITDIALOG:
return TRUE;
case WM_COMMAND:
if (LOWORD(wParam) == IDOK || LOWORD(wParam) ==
{
EndDialog(hDlg, LOWORD(wParam));
return TRUE;
}
break;
}
return FALSE;
}
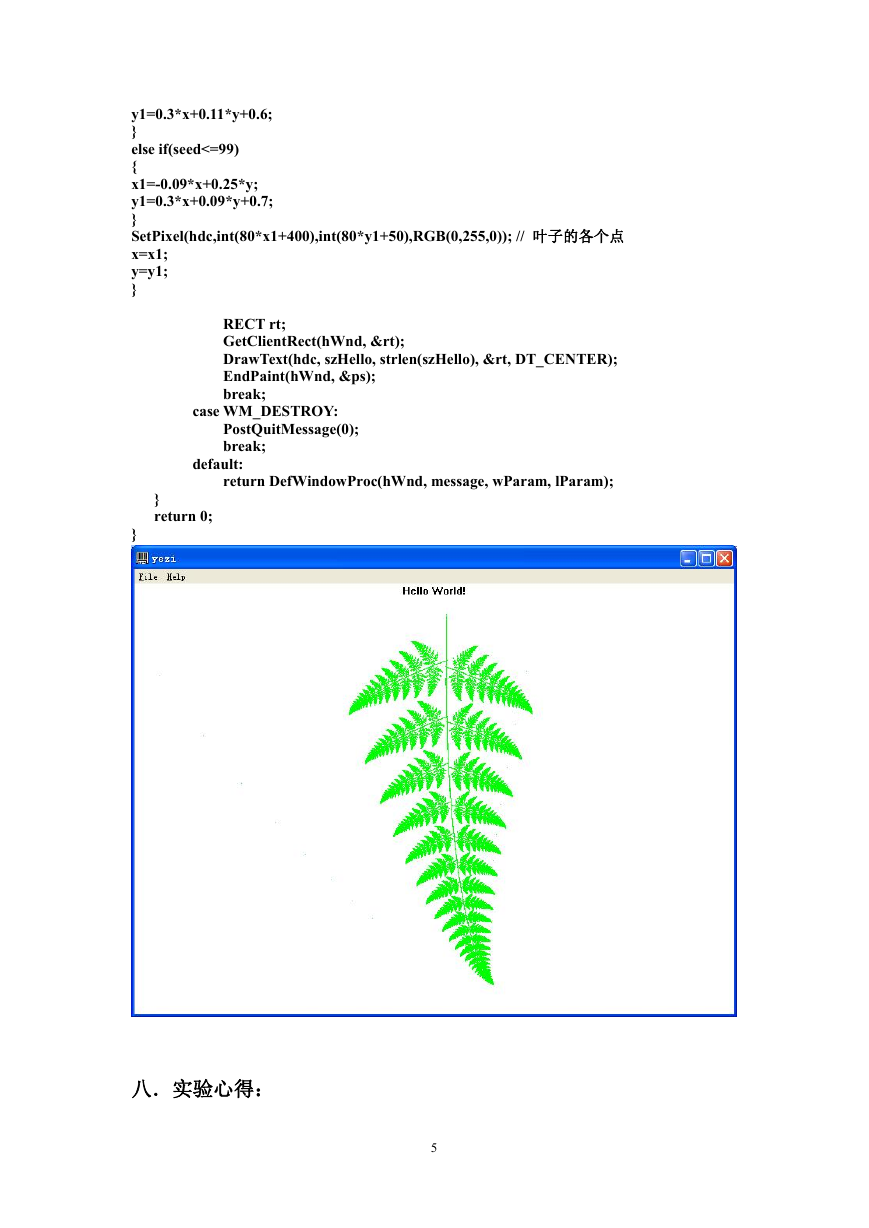
2、实验运行后的截图：
八、实验心得
实 验 报 告
实验课程：
计算机图形
学生姓名：
学
号：
专业班级：
计算机科学与技术
1
2008 年 6 月 10 日
目
录
一．实验一 VC++绘制--------------------------------------------3
二．实验二 金刚花纹--------------------------------------------7
三．实验三 平面茶壶的绘制-----------------------------------------19
四．实验四 立体茶壶的绘制----------------------------------------27
五．实验五 茶壶的着色和光照模型-------------------------------44
2
南昌大学实验报告
一． 实验名称
VC++绘制叶子
二． 实验目的
理解直线扫描生成原理，掌握直线扫描生成算法,并将其运用生成叶子算法。。
三． 实验原理
和 P1(x1,y1)；
二维基本图元直线段生成的 Bresenham 算法
0≤k（斜率）≤1 时 Bresenham 算法画直线段的步骤为：（1）输入直线的两端点 P0(x0,y0)
（2）计算初始值△x、△y、d=△x-2△y、x=x0、y=y0；
（3）绘制点(x,y)。判断 d 的符号；
若 d<0，则(x,y)更新为(x+1,y+1)，d 更新为 d+2△x-2△y；否则(x,y)更新为(x+1,y), d
更新为 d-2△y；
（4）当直线没有画完时，重复步骤 3。否则结束。
四． 实验环境
1、PC 微机；
2、DOS 操作系统或 Windows 操作系统；
3、Turbo C 程序集成环境或 Visual C++ 程序集成环境。
五． 实验要求
1、理解和掌握常用的画线原理和生成算法，以及各自特点；
2、编程实现 Bresenham 算法生成叶子；
六． 实验数据
分形几何变换：
试验所需的数据由几个线形变换组成：
a
b
0
0.85
0.09
-0.09
第一个
第二个
第三个
第四个
生成一个随机数：
取随机数在[0，1]之间取第一个
0
0.02
-0.28
0.25
c
0
-0.02
0.3
0.3
d
0.25
0.83
0.11
0.09
e
0
0
0
0
f
-0.14
1
0.6
0.7
g
0.02
0.84
0.07
0.07
[2，85]之间取第二个
[86，92]之间取第三个
3
[93，99]之间取第四个
画叶子的各个点代码：
setpixel(hdc,x,y,RGB(,,))；
七． 实验内容及运行结果
源代码节选：
int wmId, wmEvent;
PAINTSTRUCT ps;
HDC hdc;
TCHAR szHello[MAX_LOADSTRING];
LoadString(hInst, IDS_HELLO, szHello, MAX_LOADSTRING);
//x 初始值
int time=200000; //设置循环次数为 200000 次
double x=100;
double y=200;
double x1;
double y1;
int i=0;
switch (message)
{
case WM_COMMAND:
{
int seed=rand();
seed%=100;
if (seed<=1)
{
x1=0;
y1=0.25*y-0.14;
}
else if(seed<=85)
{
x1=0.85*x+0.02*y;
y1=-0.02*x+0.83*y+1;
}
else if(seed<=92)
{
x1=0.09*x-0.28*y;
4
(DLGPROC)About);
DialogBox(hInst,
(LPCTSTR)IDD_ABOUTBOX,
hWnd,
return DefWindowProc(hWnd, message, wParam, lParam);
wmId
= LOWORD(wParam);
wmEvent = HIWORD(wParam);
// Parse the menu selections:
switch (wmId)
{
case IDM_ABOUT:
break;
case IDM_EXIT:
DestroyWindow(hWnd);
break;
default:
}
break;
case WM_PAINT:
hdc = BeginPaint(hWnd, &ps);
for(i=0;i
y1=0.3*x+0.11*y+0.6;
}
else if(seed<=99)
{
x1=-0.09*x+0.25*y;
y1=0.3*x+0.09*y+0.7;
}
SetPixel(hdc,int(80*x1+400),int(80*y1+50),RGB(0,255,0)); // 叶子的各个点
x=x1;
y=y1;
}
RECT rt;
GetClientRect(hWnd, &rt);
DrawText(hdc, szHello, strlen(szHello), &rt, DT_CENTER);
EndPaint(hWnd, &ps);
break;
case WM_DESTROY:
PostQuitMessage(0);
break;
return DefWindowProc(hWnd, message, wParam, lParam);
default:
}
return 0;
}
八．实验心得：
5
这是第一个计算机图形的试验，所以一开始对试验环境摸索了很久。因为虽然也是用的 vc
++来编译程序，但是和以前不一样。在这里我们需要新建一个“hello world”程序，然后在
进行程序的编写，再把编写好的程序插进去后运行出结果。
南昌大学实验报告
一、 实验名称
金刚花纹
二、 实验目的
理解和掌握二、三维图形的基本裁剪的原理和算法。
三、 实验原理
最简单的裁剪方法是把各种图形扫描转换为点之后，再判断各点是否在窗内。但
那样太费时，一般不可取。这是因为有些图形组成部分全部在窗口外，可以完全排除，
不必进行扫描转换。所以一般采用先裁剪再扫描转换的方法，多边形裁剪示意图，如图
4-1 所示。
（a）裁剪前
（b）裁剪后
图 4-1 多边形裁剪示意图
6
直线段裁剪算法是复杂图形裁剪的基础，复杂的曲线可以通过折线段来近似，从而裁
剪问题也可以化为直线段的裁剪问题。直线和窗口的关系如图 2.2 所示，可以分为如下 3
类：
图 4-2 直线与窗口的关系
（1）整条直线在窗口内，此时，不需剪裁，显示整条直线。
（2）整条直线在窗口外，此时，不需剪裁，不显示整条直线。
（3）部分直线在窗口内，部分直线在窗口外。此时，需要求出直线与窗框的交点，并将窗
口外的直线部分剪裁掉，显示窗口内的直线部分。
直线剪裁算法有两个主要步骤。首先将不需剪裁的直线挑出，即删去在窗外的直线。然
后，对其余直线，逐条与窗框求交点，并将窗口外的部分删去。
直线剪裁算法有两个主要步骤：首先将不需剪裁的直线挑出，并删去其中在窗外的直
线。然后，对其余直线，逐条与窗框求交点，并将窗外部分删去。
2、梁友栋—Barsky 裁剪算法描述
一条两端点为 P1（x1，y1）、P2（x2，y2）的线段可以用参数方程形式表示：
x= x1+ u·（x2-x1）= x1+ u·Δx
y= y1+ u·（y2-y1）= y1+ u·Δy
式中，Δx=x2-x1，Δy=y2-y1，参数 u 在 0～1 之间取值，P（x，y）代表了该线段上的
一个点，其值由参数 u 确定，由公式可知，当 u=0 时，该点为 P1（x1，y1），当 u=1 时，该
点为 P2（x2，y2）。如果点 P（x，y）位于由坐标（XL，YB）和（XR，YT）所确定的窗口内，
那么下式成立：
0≤u≤1
XL≤x1+ u·Δx≤XR
这四个不等式可以表示为：u·pk ≤qk ， k=1，2，3，4
其中，p、q 定义为：
YB≤y1+ u·Δy≤YT
p1=-Δx， q1=x1-XL
p3=-Δy， q3=y1-YB
p2= Δx， q2=XR-x1
p4= Δy， q4=YT-y1
从上式可以知道：任何平行于窗口某边界的直线，其 pk=0，k 值对应于相应的边界（k=1，
2，3，4 对应于左、右、下、上边界）。如果还满足 qk<0，则线段完全在边界外，应舍弃该
线段。如果 pk=0 并且 qk≥0，则线段平行于窗口某边界并在窗口内，见图 4-3 所示。
（1）当 pk<0 时，线段从裁剪边界延长线的外部延伸到内部；
（2）当 pk>0 时，线段从裁剪边界延长线的内部延伸到外部；
Y
C
O
7
D
F
E
B
A
X
图 4-3
pk =0 的情况
例如，当Δx≥0 时，对于左边界 p1<0（p1=-Δx），线段从左边界的外部到内部；对于
右边界 p2>0（p2=Δx），线段从右边界的内部到外部。
当Δy<0 时，对于下边界 p3>0（p3=-Δy），线段从下边界的内部到外部；对于上边界
p4<0（p4=Δy），线段从上边界的外部到内部。
（3）当 pK≠0 时，可以计算出参数 u 的值，它对应于无限延伸的直线与延伸的窗口边界 k
的交点，即：u= qk/pk
对于每条直线，可以计算出参数 u1 和 u2，该值定义了位于窗口内的线段部分：
1）u1 的值由线段从外到内遇到的矩形边界所决定（pk<0），对这些边界计算 rk=qk/pk，
u1 取 0 和各个 r 值之中的最大值。
2）u2 的值由线段从内到外遇到的矩形边界所决定（pk>0），对这些边界计算 rk=qk/pk，
u2 取 0 和各个 r 值之中的最小值。
3）如果 u1>u2，则线段完全落在裁剪窗口之外，应当被舍弃；否则，被裁剪线段的端点
可以由 u1 和 u2 计算出来。
3、梁友栋-Barsky 裁剪算法的实现
1）初始化线段交点的参数：u1=0，u2=1；
2）计算出各个裁剪边界的 p、q 值；
3）调用函数 clipTest()，在函数中根据 p、q 来判断：是舍弃线段还是改变交点的参数。
当 p<0 时，参数 r 用于更新 u1；（u1=max{u1，…，rk}）
当 p>0 时，参数 r 用于更新 u2。（u2=min{u2，…，rk}）
如果更新了 u1 或 u2 后，使 u1>u2，则舍弃该线段。
当 p=0 且 q<0 时，因为线段平行于边界并且位于边界之外，则舍弃该线段。见下图 4-4
所示。
d、p、q 的四个值经判断后，如果该线段未被舍弃，则裁剪线段的端点坐标由参数 u1 和 u2
图 4-4
P=0 而且 q<0 的情况
的值决定。
4、程序流程图的设计
8
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
