算法报告 团队名称：bug 1 运行环境 操作系统：Windows 7 平台：Visual studio 2013 语言：C++ 2 算法原理 首先定义几个下文中用到的名称 特殊点：表示存储间和水果间的节点，用 和 表示 特殊边：表示必须经过的边，用 表示。 2.1 基本思路 本算法的基本思想是先考虑特殊点和特殊边的访问顺序，确定好特殊点和特殊边的访 问顺序之后，再逐个计算相邻特殊点或特殊边的最短路径，计算两点间的最短路径使用 Dijstra 算法，本文不再赘述。最后将这些最短路径拼接起来，得到一条从起始节点到目的 节点的完整路径。在编程实现时，是对特殊点和特殊边进行全排列来计算所有可能的排列， 并对每一种排列都计算从起始节点到目的节点的完整路径。实际上每一条完整路径都满足 经过指定点和指定边的要求，从计算结果中选择满足节点数限制，并且费用最低的路径作 为输出结果。 如果所有的路径都不能满足节点数小于等于 9 的要求，那么选择费用最低的结果作为次优 参考路径输出。 2.2 算法流程 一、首先确定特殊点的访问顺序。先检查两个特殊点是否有可能刚好是某条特殊边的端点， 如果是则剔除掉，因为在后续插入所有特殊边时相当于也插入了两个特殊点，所以在 确定特殊点的访问顺序时不用考虑在内。那么剩下的特殊点有可能是 ， ， ， 四种情况，如果是只有一个特殊点或者没有特殊点的情况，那么 特殊点的访问顺序也就确定了；如果是两个特殊点的情况，那么就有可能有 和 两种特殊点的访问顺序。 二、对于步骤一中获得的每一种特殊点访问顺序，将所有特殊边逐一插入到特殊点排列中， 形成一种特殊点/特殊边的访问顺序。其中，特殊边可以插入到特殊点排列的任意位置。 例如一个有 2 个特殊点的排列 ，那么一条特殊边 可以有 3 个插入位 置 ， 分 别 为 ， ， 。 并 且 和 表示不同的特殊边，因为从节点 i 到节点 j 和节点 j 到节点 i 明显 是两种不同的访问顺序。通过步骤二就可以得到在有限制必须经过的点和必须经过的 边的条件下，这些特殊点和特殊边访问的先后顺序。 

三、对步骤二得到的特殊点和特殊边的访问序列，计算相邻特殊点或特殊边的最短访问路 径。 如果在访问序列中，特殊边 和特殊点 相邻，那么实际上就是计算节点 到节点 的最短路径。另外，剪枝操作可以在该步骤中进行，在计算相邻的特殊 点或特殊边的最短路径时，如果从起始节点到当前节点的节点数已超过限制，那么就 不再往下计算，而是选择新的特殊点序列进行特殊边的插入。 四、将步骤三中得到的相邻特殊点或特殊边之间的最短路径拼接起来，得到过指定点和指 定边的完整路径。 3 算法实现结果分析 算法实验使用赛事官方提供的拓扑图以及自己修改的拓扑图数据作为实验数据，数据 使用 TXT 文本文件存储（数据格式在 readme.txt 中说明）。 第一个拓扑图数据（data0.txt）如下： 在程序运行过程中的关键步骤及结果。如下表（S 节点和 E 节点分别用 N0 和 N17 表示）： 表 1：算法关键步骤及结果 图 1 拓扑图 关键步骤 求特殊点的全排列 插入特殊边 结果 （N7,N12），（N12,N7） 得到 48 个排列顺序。 第一条特殊边可以插入特殊点序列的位置 有 3 个 ， 第 二 条 特 殊 边 有 4 个 插 入 位 置 （第一条特殊边插入后，它的左右两边也 视为可以插入的位置）。另外，每条特殊 边的两个端点互换表示不同结果，所以每 次插入结果数目都要翻倍。所以 2 条特殊 边，2 个特殊点，那么需要遍历计算的特 殊 点 / 特 殊 边 的 排 列 顺 序 有 个。 计算相邻特殊点或特殊边之间的最短路径 以排列顺序 N0 N7 （N2 N4） N12 （N14 N13） N17 为例（N0,N17 分别表示起始和 目的节点）。 求得最短路径结果： 

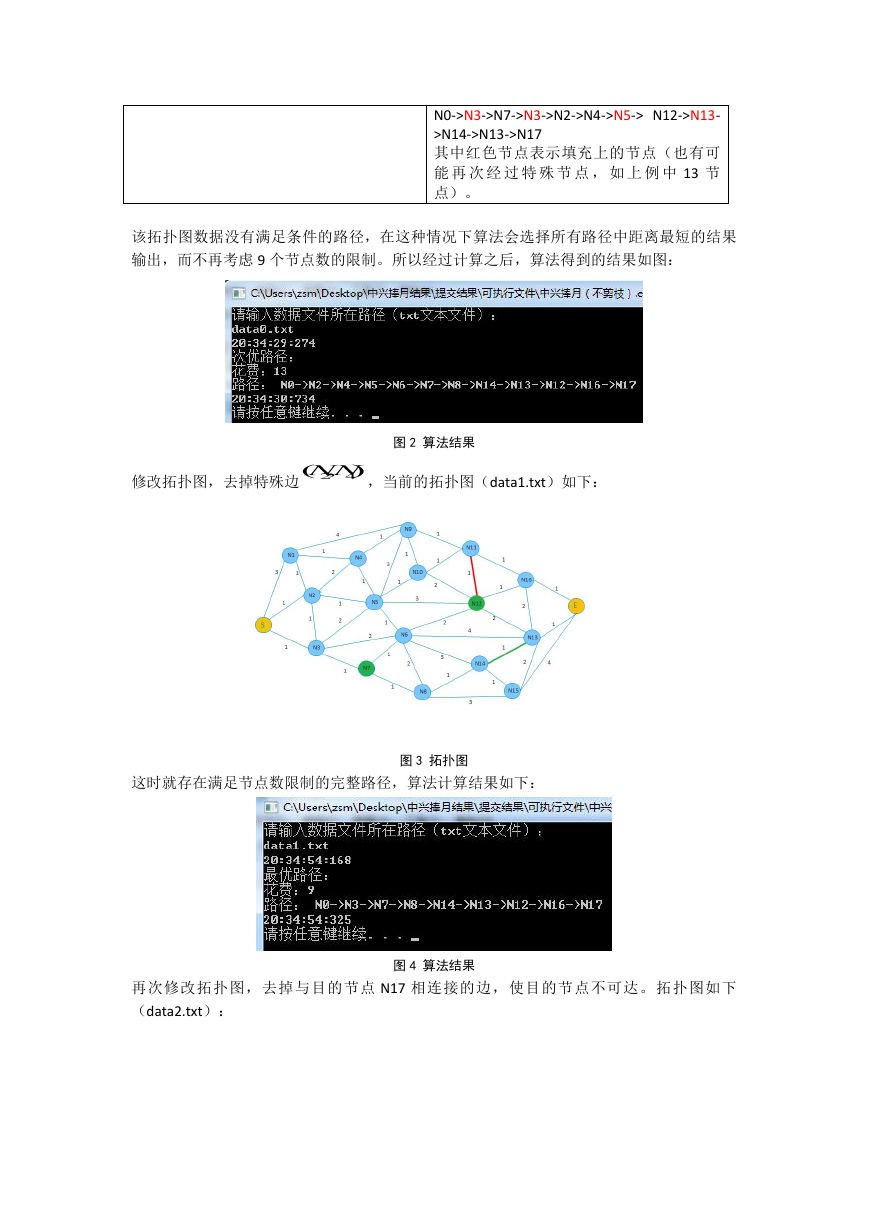
N0->N3->N7->N3->N2->N4->N5-> N12->N13- >N14->N13->N17 其中红色节点表示填充上的节点（也有可 能 再 次 经 过 特 殊 节 点 ， 如 上 例 中 13 节 点）。 该拓扑图数据没有满足条件的路径，在这种情况下算法会选择所有路径中距离最短的结果 输出，而不再考虑 9 个节点数的限制。所以经过计算之后，算法得到的结果如图： 修改拓扑图，去掉特殊边 ，当前的拓扑图（data1.txt）如下： 图 2 算法结果 这时就存在满足节点数限制的完整路径，算法计算结果如下： 图 3 拓扑图 再次修改拓扑图，去掉与目的节点 N17 相连接的边，使目的节点不可达。拓扑图如下 （data2.txt）： 图 4 算法结果 

算法在搜索路径时，发现没有任意一个特殊点或特殊边可以到达目的节点 E，所以在遍历 完所有特殊点和特殊边的全排列顺序后，输出无解，如图所示。 图 5 拓扑图 图 6 算法结果 为试验特殊边数目对算法复杂度的影响，本文在官方给出的拓扑图数据上随机添加若 干条特殊边，得到以下试验结果（运行结果都未进行剪枝，如果不存在满足全部要求的路 径，那么算法会输出次优路径，算法时间包括次优路径的计算）。 图的节点总数 特殊边个数 特殊点/边全排列数 目 时间消耗/ms 表二 算法在不同特殊边数目的执行时间表 18（data3.txt） 4 5760 18（data0.txt） 2 48 18（data4.txt） 8 464486400 1503 4023 >10000000 其次在相同特殊边的情况下，增大这个拓扑图的节点数目和连接边的数量，比较算法 的运行时间。 图的节点总数 特殊边个数 特殊点/边全排列数 目 时间消耗/ms 表三 算法在不同节点数目的执行时间表 24（data6.txt） 2 48 18（data5.txt） 2 48 36（data7.txt） 2 48 322 360 534 从实验结果来看： 1、 本方法对于网络节点的大小数目并不敏感，这是因为在特殊边数目和位置不发生改变 的情况下，需要计算的次数实际上并未增加，只是在计算相邻特殊点或特殊边的最短 

距离时会增加部分计算量，基本可以忽略不计。 2、 算法对特殊边的数目很敏感。当特殊边数量增加时，算法需要遍历计算的路径呈指数 增加。以特殊点都不是特殊边的端点这种情况为例，那么如果有 n 条特殊边，那么对 每一种特殊点排列，特殊边插入后的可能排序有 个，需要通过剪枝降低 复杂度。