BUCK电路的环路计算，补偿和仿真.pdf-资料库

weixin_38744435-11753887-16359647553574886493.pdf-第1页.png

第1页 / 共18页

weixin_38744435-11753887-16359647553574886493.pdf-第2页.png

第2页 / 共18页

weixin_38744435-11753887-16359647553574886493.pdf-第3页.png

第3页 / 共18页

weixin_38744435-11753887-16359647553574886493.pdf-第4页.png

第4页 / 共18页

weixin_38744435-11753887-16359647553574886493.pdf-第5页.png

第5页 / 共18页

weixin_38744435-11753887-16359647553574886493.pdf-第6页.png

第6页 / 共18页

weixin_38744435-11753887-16359647553574886493.pdf-第7页.png

第7页 / 共18页

weixin_38744435-11753887-16359647553574886493.pdf-第8页.png

第8页 / 共18页

BUCK 电路的环路计算，补偿和仿真 Xia Jun 2010-8-14 本示例从简单的 BUCK 电路入手，详细说明了如何进行电源环路的计算和补偿，并通过 saber 仿真验证环路补偿的合理性。一直以来，环路的计算和补偿都是开关电源领域的“难点”，很多做开关电源研发的工程师要么对环路一无所知，要么是朦朦胧胧，在产品的开发过程中，通过简单的调试来确定环路补偿参数。而这种在实验室里调试出来的参数真的能满足各种实际的使用情况吗？能保证电源产品在高低温的情况下，在各种负载条件下，环路都能够稳定吗？能保证在负载跳变的情况下收敛吗？太多的未知数，这是产品开发的大忌。我们必须明明白白的知道，环路的稳定性如何？相位裕量是多少？增益裕量是多少？高低温情况下这些值又会如何变化？在一些对动态要求非常严格的场合，我们如何折中考虑环路稳定性和动态响应之间的关系？有的放矢，通过明确的计算和仿真，我们的产品设计才是科学的，合理的，可靠的。我们的目标是让产品经得起市场的检验，让客户满意，让自己放心。一切从闭环系统的稳定性说起，在自动控制理论中，根据乃奎斯特环路稳定性判据，如果负反馈系统在穿越频率点的相移为 180°，那么整个闭环系统是不稳定的。很多人可能对这句话很难理解，虽然自动控制理论几乎是所有大学工科学生的必修课，可大部分是是抱着应付的态度的，学完就忘了。那就再给大家讲解一下吧。等式：Vout=[Vin-Vout*H(S)]*G(S) Vout Vin 1 + G S( ) ⋅ G S( ) H S( ) 公式： G(S)/(1+G(S)*H(S))就称之为系统的闭环传递函数，如果 1+G(S)*H(S)=0，那么闭环系统的输出值将会无限大，此时闭环系统是不收敛的，也即是不稳定的。 G(S)*H(S)是系统的开环传递函数，当 G(S)*H(S)=-1 时，以 S=jω 带入，即获得开环系统的频域响应为 G(jω)*H(jω)=-1，此时频率响应的增益和相角分别为： gain=‖-1‖=1 angle=tan-1(0/-1)=180° 从上面的分析可以看出，如果扰动信号经过 G(S)和 H(S)后，模不变，相位改变 180°，那么这个闭环系统就是不稳定的。但是，别忘了，这是负反馈系统，信号经过 H(S)之后，本身就有 180°的相移，所以，针对负反馈的闭环系统而言，其描述为：如果扰动信号经过系统主电路和反馈系统之后，其模不变，相位也不变，那么这个系统是不稳定的。为什么相位也不变？因为 G(S)*H(S)造成的 180°相移和负反馈本身造成的 180°相移，两者叠加之后是 360°，所以等于相位不变。什么是穿越频率？ G(S)*H(S)对应的增益为 1（即幅值不变）的频率即为穿越频率。换算为 dB 单位： 20log1=0dB。

理论上来说，在穿越频率点上，只要相移不是 180°，那么系统就是稳定的。但是由于模拟系统的离散性（即所有器件的特性都不是固定不变的，随时间和温度在不断的变化），如果相移很接近 180°，这时闭环系统是条件稳定的，即有可能进入不稳定状态。所以为了避免这种情况，要求在穿越频率点上，开环传递函数 G(S)*H(S)的相移应该与 180°保持足够的裕量。这个裕量选取多少比较合适呢？目前在工程应用上通常选取 45°，即要求传递函数 G(S)*H(S)的相移应该小于 135°，这是兼顾考虑环路稳定性和动态响应速度的折中值，理论上来说裕量越大越好，但过大的相位裕量会导致动态响应变慢（过阻尼特性）。为了保证足够的相位裕量，我们希望开环传递函数的增益曲线以-1 的斜率穿越 0dB 线。如果开环传递函数的增益曲线在穿越频率点的斜率为-2，那么意味着有接近 180°的相移，这将导致相位裕量明显不足，而如果斜率为-1，那么通常意味着相位有 45°以上的裕量。增益曲线的斜率是如何来的？主电路或反馈补偿电路中，每产生一个极点，开环传递函数的增益曲线斜率在该极点的转折频率点上就会增加-1，相反的，每产生一个零点，开环传递函数的增益曲线斜率在该零点的转折频率点上就会增加+1。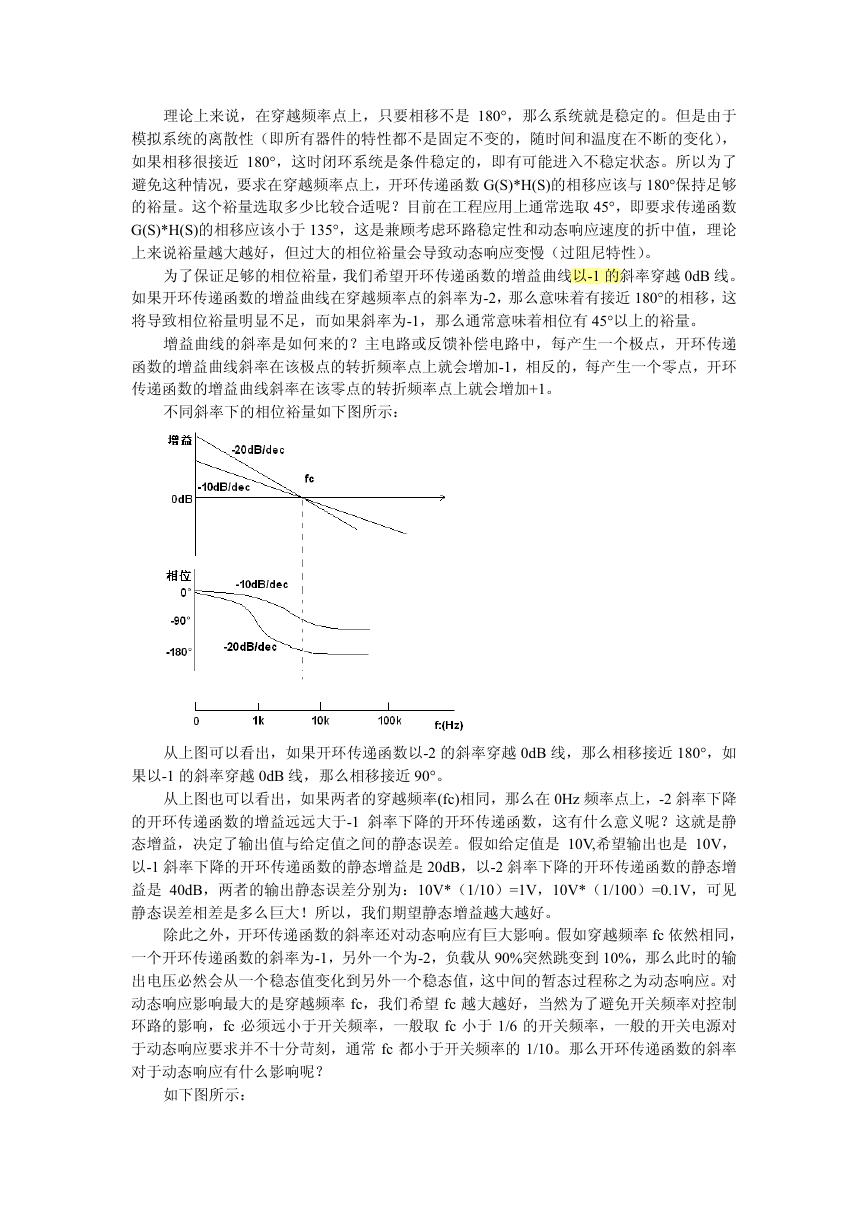不同斜率下的相位裕量如下图所示：从上图可以看出，如果开环传递函数以-2 的斜率穿越 0dB 线，那么相移接近 180°，如果以-1 的斜率穿越 0dB 线，那么相移接近 90°。从上图也可以看出，如果两者的穿越频率(fc)相同，那么在 0Hz 频率点上，-2 斜率下降的开环传递函数的增益远远大于-1 斜率下降的开环传递函数，这有什么意义呢？这就是静态增益，决定了输出值与给定值之间的静态误差。假如给定值是 10V,希望输出也是 10V，以-1 斜率下降的开环传递函数的静态增益是 20dB，以-2 斜率下降的开环传递函数的静态增益是 40dB，两者的输出静态误差分别为：10V*（1/10）=1V，10V*（1/100）=0.1V，可见静态误差相差是多么巨大！所以，我们期望静态增益越大越好。除此之外，开环传递函数的斜率还对动态响应有巨大影响。假如穿越频率 fc 依然相同，一个开环传递函数的斜率为-1，另外一个为-2，负载从 90%突然跳变到 10%，那么此时的输出电压必然会从一个稳态值变化到另外一个稳态值，这中间的暂态过程称之为动态响应。对动态响应影响最大的是穿越频率 fc，我们希望 fc 越大越好，当然为了避免开关频率对控制环路的影响，fc 必须远小于开关频率，一般取 fc 小于 1/6 的开关频率，一般的开关电源对于动态响应要求并不十分苛刻，通常 fc 都小于开关频率的 1/10。那么开环传递函数的斜率对于动态响应有什么影响呢？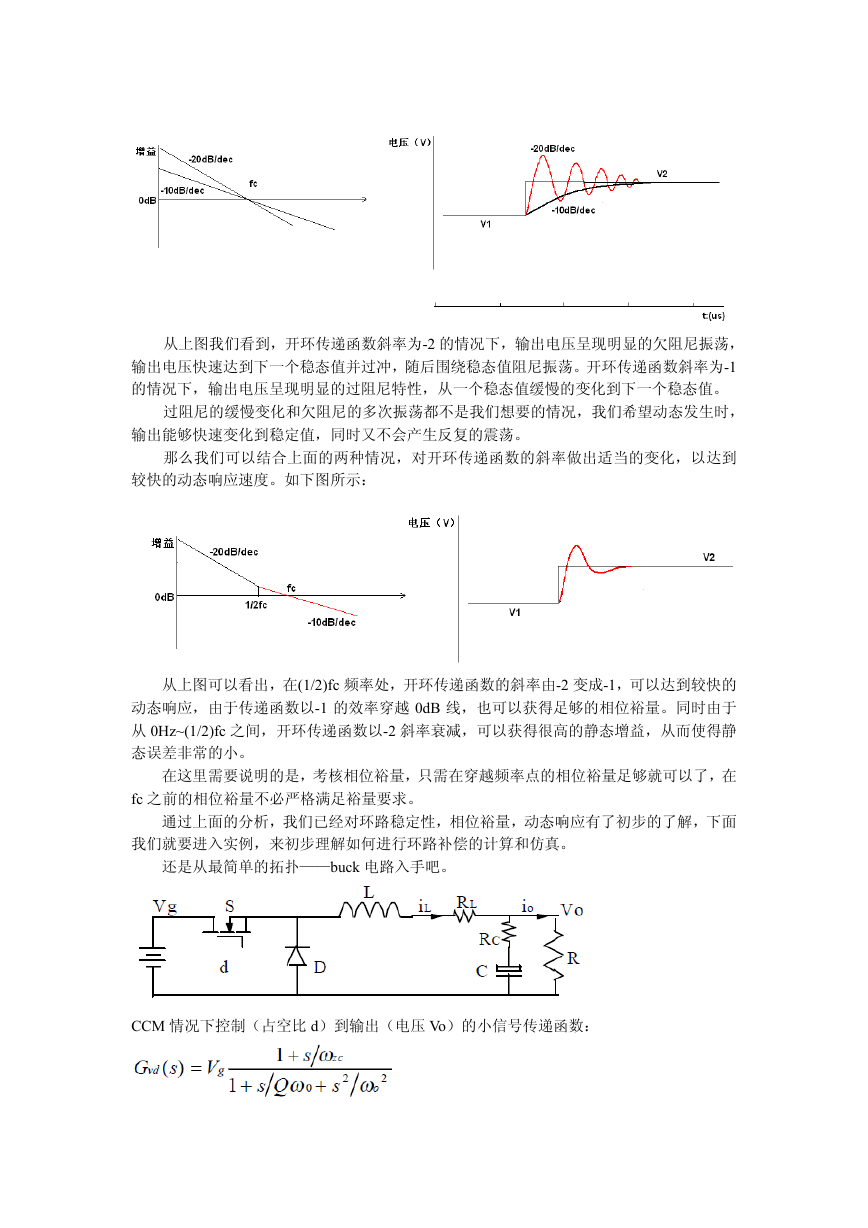如下图所示：

从上图我们看到，开环传递函数斜率为-2 的情况下，输出电压呈现明显的欠阻尼振荡，输出电压快速达到下一个稳态值并过冲，随后围绕稳态值阻尼振荡。开环传递函数斜率为-1 的情况下，输出电压呈现明显的过阻尼特性，从一个稳态值缓慢的变化到下一个稳态值。过阻尼的缓慢变化和欠阻尼的多次振荡都不是我们想要的情况，我们希望动态发生时，输出能够快速变化到稳定值，同时又不会产生反复的震荡。那么我们可以结合上面的两种情况，对开环传递函数的斜率做出适当的变化，以达到较快的动态响应速度。如下图所示：从上图可以看出，在(1/2)fc 频率处，开环传递函数的斜率由-2 变成-1，可以达到较快的动态响应，由于传递函数以-1 的效率穿越 0dB 线，也可以获得足够的相位裕量。同时由于从 0Hz~(1/2)fc 之间，开环传递函数以-2 斜率衰减，可以获得很高的静态增益，从而使得静态误差非常的小。在这里需要说明的是，考核相位裕量，只需在穿越频率点的相位裕量足够就可以了，在 fc 之前的相位裕量不必严格满足裕量要求。通过上面的分析，我们已经对环路稳定性，相位裕量，动态响应有了初步的了解，下面我们就要进入实例，来初步理解如何进行环路补偿的计算和仿真。还是从最简单的拓扑——buck 电路入手吧。 CCM 情况下控制（占空比 d）到输出（电压 Vo）的小信号传递函数：

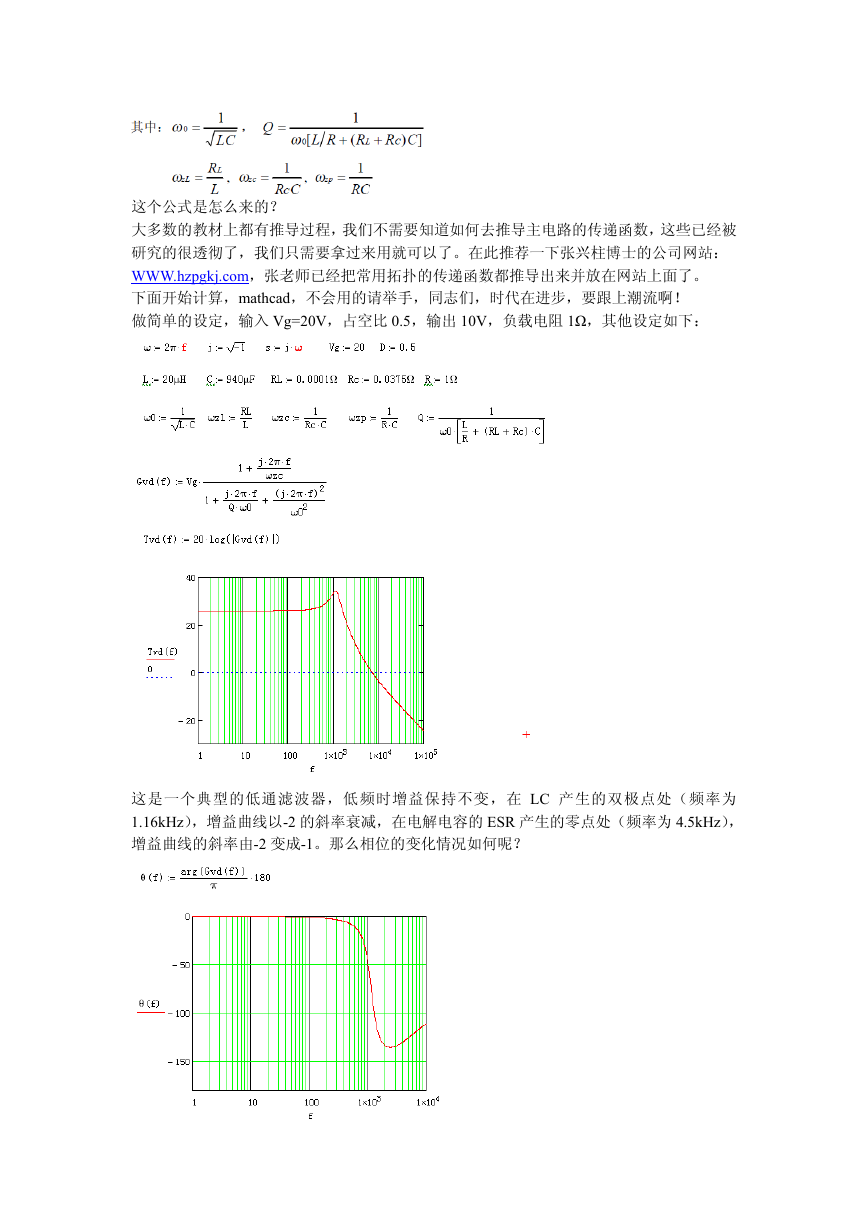
这个公式是怎么来的？大多数的教材上都有推导过程，我们不需要知道如何去推导主电路的传递函数，这些已经被研究的很透彻了，我们只需要拿过来用就可以了。在此推荐一下张兴柱博士的公司网站： WWW.hzpgkj.com，张老师已经把常用拓扑的传递函数都推导出来并放在网站上面了。下面开始计算，mathcad，不会用的请举手，同志们，时代在进步，要跟上潮流啊！做简单的设定，输入 Vg=20V，占空比 0.5，输出 10V，负载电阻 1Ω，其他设定如下：这是一个典型的低通滤波器，低频时增益保持不变，在 LC 产生的双极点处（频率为 1.16kHz），增益曲线以-2 的斜率衰减，在电解电容的 ESR 产生的零点处（频率为 4.5kHz），增益曲线的斜率由-2 变成-1。那么相位的变化情况如何呢？

看起来还不错，电容 ESR 引起的零点部分抵消了 LC 双极点导致的相移，使得在穿越频率点上还保持足够的相位裕量：从上面的计算中，可以获得主电路传递函数 G(S)的穿越频率为 7.2kHz，相位裕量为 62.4°。看来我们不需要做补偿啊，穿越频率够大，在穿越频率点上传递函数增益曲线的斜率为-1，相位裕量也大于 45°，只要让 H(S)=1 就可以保证开环传递函数 G(S)*H(S)获得足够的相位裕量。可是，静态增益实在太低了，只有 26dB，我们要消除静态误差，就必须使得增益曲线从 0Hz 开始就以-1 或-2 的斜率下降，补偿是不可避免的。下面就几种典型的补偿方式做一下介绍： 1. 单极点补偿

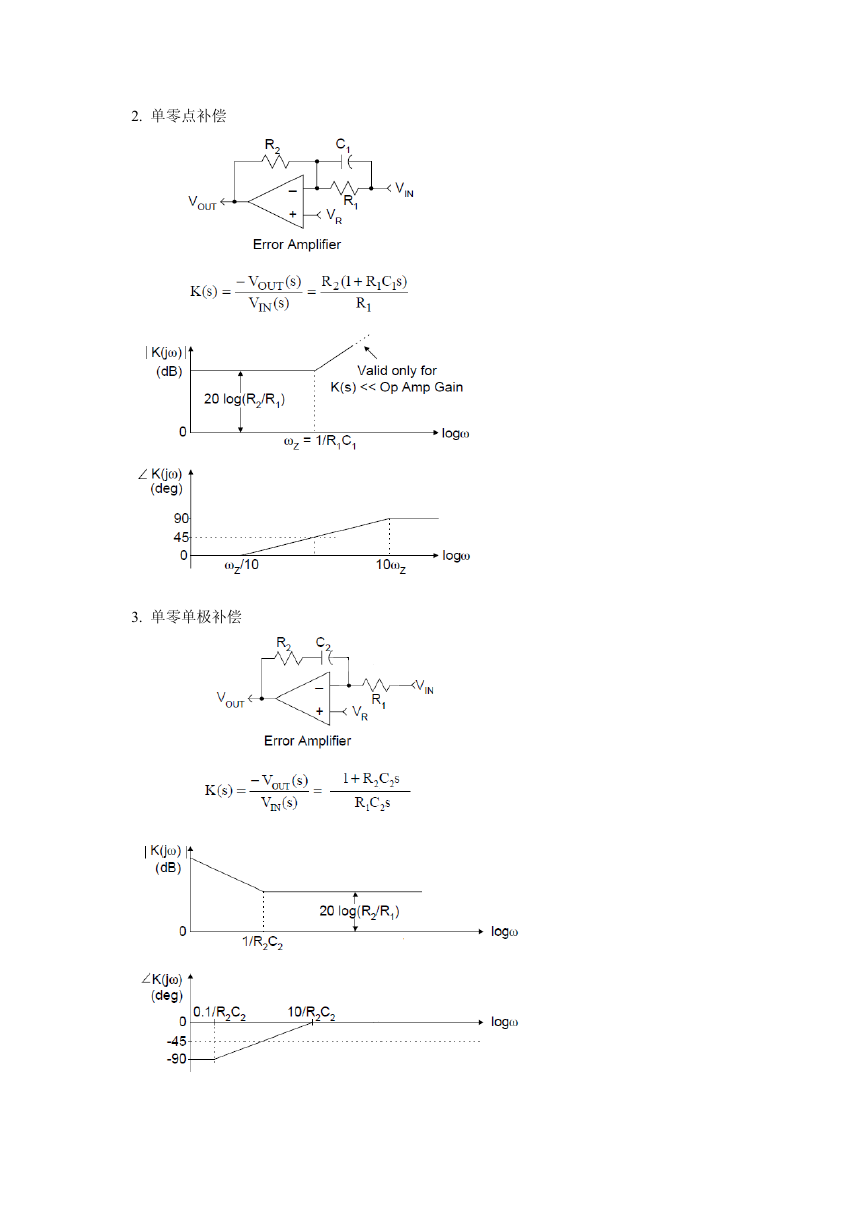
2. 单零点补偿 3. 单零单极补偿

4. 双零单极补偿 5. 单零双极补偿 6. 双零双极补偿

根据以上的各种补偿电路，我们应该选择哪一个呢？为了提高静态增益，我们需要在原点处产生一个极点，所以如果要做最简单的补偿，我们应该采用单零单极补偿电路。假如我们希望开环传递函数 G(S)*H(S)的穿越频率为 10kHz，而前面计算的 G(S)的穿越频率为 7.2kHz，那么 H(S)将把整体的穿越频率往后推延 2.8kHz。 H(S)由两部分组成，一部分是我们需要设计的补偿环节 K(S)，另一部分是 PWM 的调制比，即占空比与调制锯齿波电压幅值之间的比例，称之为 Fm，如下图所示：

资料库

BUCK电路的环路计算，补偿和仿真.pdf

相关推荐

开发技术

热门标签

最新资料