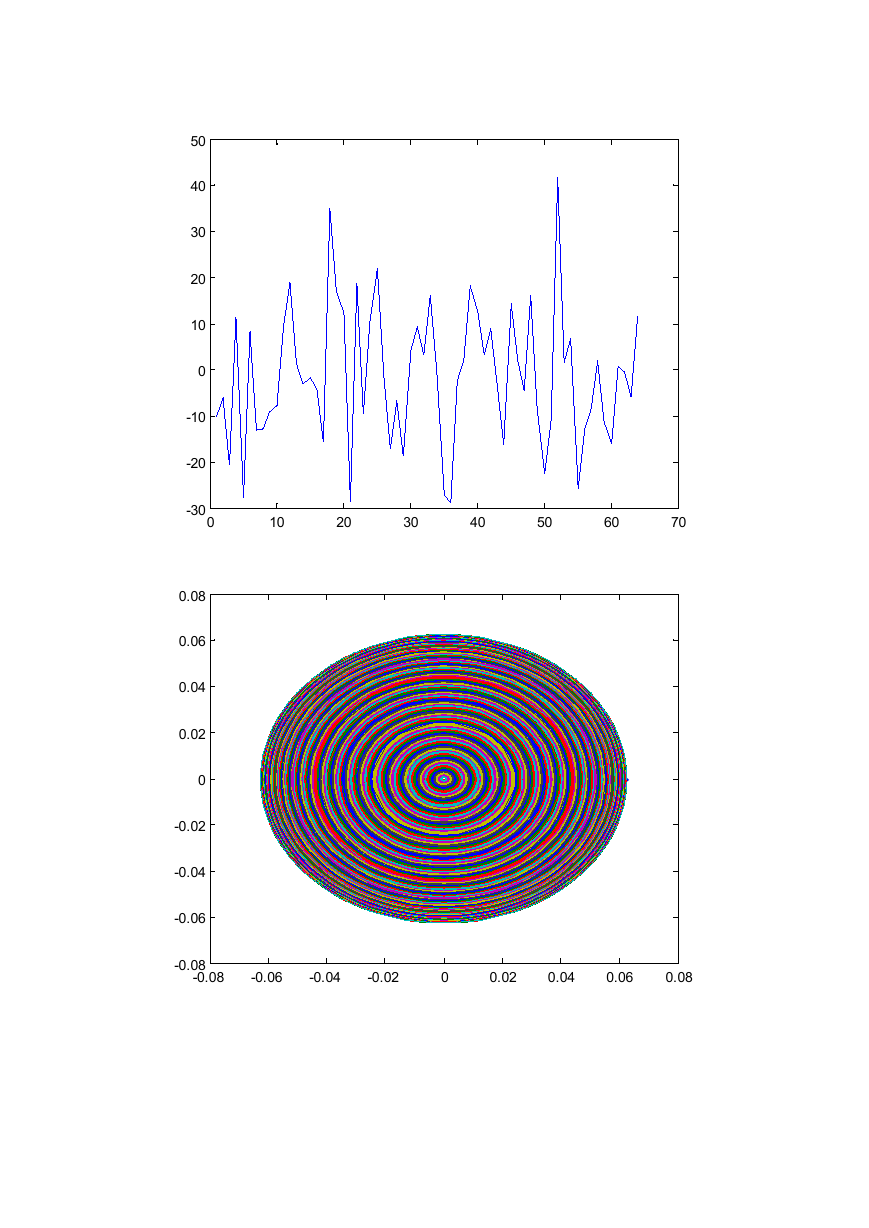
clc;clear %% 1. 时域测试信号生成 % 稀疏度(做 FFT 可以看出来) K=7; % 信号长度 N=256; % 测量数(M>=K*log(N/K),至少 40,但有出错的概率) M=64; % 信号频率 1 f1=50; f2=100; % 信号频率 2 f3=200; % 信号频率 3 f4=400; % 信号频率 4 fs=800; % 采样频率 ts=1/fs; % 采样间隔 Ts=1:N; % 采样序列 x=0.3*cos(2*pi*f1*Ts*ts)+0.6*cos(2*pi*f2*Ts*ts)+0.1*cos(2*pi*f3*Ts*ts)+0.9*cos(2*pi*f4*Ts *ts); % 完整信号 %% 2. 时域信号压缩传感 Phi=randn(M,N); s=Phi*x.'; % 测量矩阵(高斯分布白噪声) % 获得线性测量 %% 3. 正交匹配追踪法重构信号(本质上是 L_1 范数最优化问题) m=2*K; Psi=fft(eye(N,N))/sqrt(N); T=Phi*Psi'; % 傅里叶正变换矩阵 % 算法迭代次数(m>=K) % 恢复矩阵(测量矩阵*正交反变换矩阵) hat_y=zeros(1,N); Aug_t=[]; r_n=s; for times=1:m; for col=1:N; % 待重构的谱域(变换域)向量 % 增量矩阵(初始值为空矩阵) % 残差值 % 迭代次数(有噪声的情况下,该迭代次数为 K) % 恢复矩阵的所有列向量 product(col)=abs(T(:,col)'*r_n); %恢复矩阵的列向量和残差的投影系数(内积值) end [val,pos]=max(product); Aug_t=[Aug_t,T(:,pos)]; T(:,pos)=zeros(M,1); 为了简单我把它置零） % 最大投影系数对应的位置 % 矩阵扩充 % 选中的列置零（实质上应该去掉， aug_y=(Aug_t'*Aug_t)^(-1)*Aug_t'*s; r_n=s-Aug_t*aug_y; pos_array(times)=pos; % 最小二乘,使残差最小 % 残差 % 纪录最大投影系数的位置 end hat_y(pos_array)=aug_y; hat_x=real(Psi'*hat_y.'); % 重构的谱域向量 % 做逆傅里叶变换重构得到时域信号 

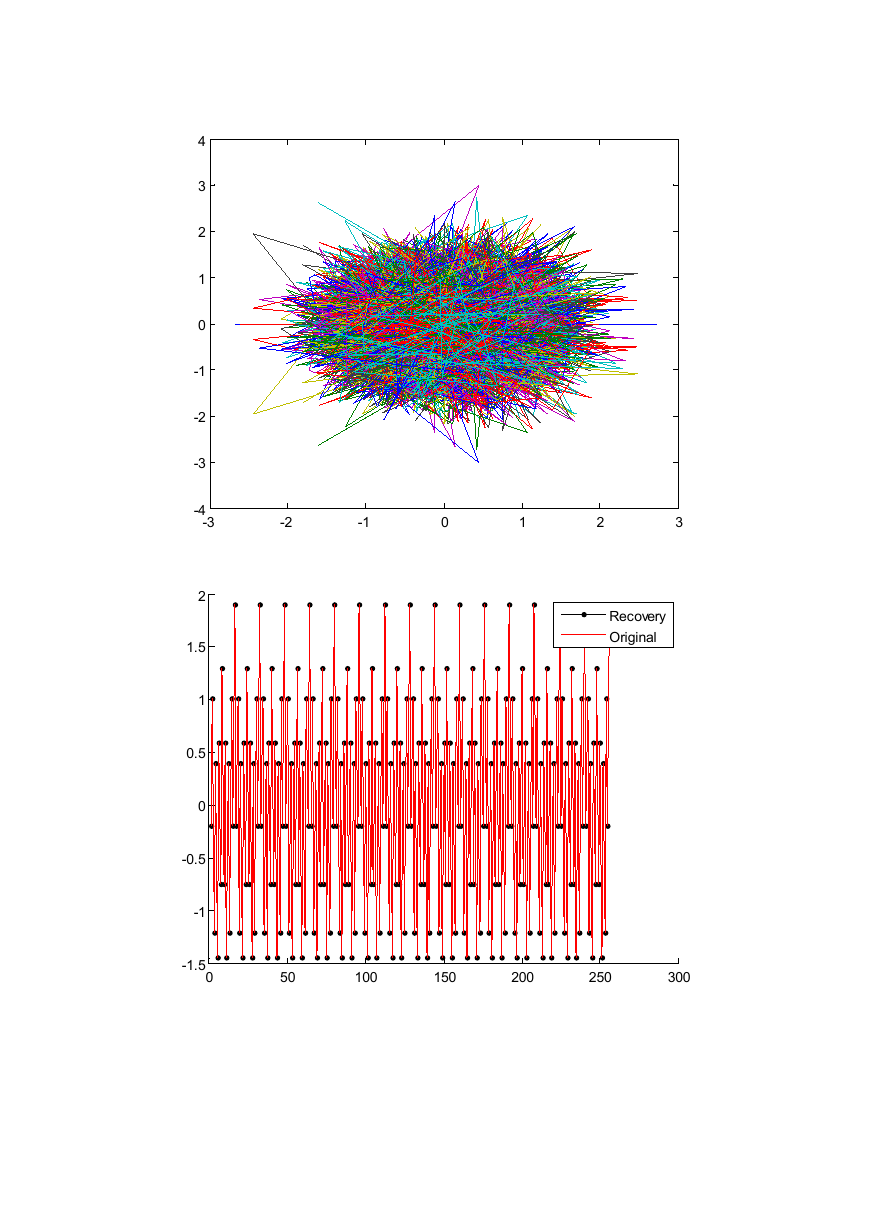
%% 4. 恢复信号和原始信号对比 figure(1); hold on; plot(hat_x,'k.-') plot(x,'r') legend('Recovery','Original') norm(hat_x.'-x)/norm(x) % 重建信号 % 原始信号 % 重构误差 

2 1.5 1 0.5 0 -0.5 -1 -1.5 0 5 4 3 2 1 0 -1 -2 -3 -4 0 50 100 150 200 250 300 10 20 30 40 50 60 70 

50 40 30 20 10 0 -10 -20 -30 0 0.08 0.06 0.04 0.02 0 -0.02 -0.04 -0.06 10 20 30 40 50 60 70 -0.08 -0.08 -0.06 -0.04 -0.02 0 0.02 0.04 0.06 0.08 

4 3 2 1 0 -1 -2 -3 -4 -3 2 1.5 1 0.5 0 -0.5 -1 -1.5 0 -2 -1 0 1 2 3 Recovery Original 50 100 150 200 250 300