2 第 16 卷 第 5 期 V o l. 16 N o. 5 　　文章编号: 1001 2 0920 (2001) 05 2 05 0612 2 　控　制　与　决　策 CON T ROL 　A N D 　D EC IS ION 　 2001 年 9 月 　 Sep t. 2001 基于滑模位置控制的机器人灵巧手 模糊自适应阻抗控制 姜　力, 蔡鹤皋, 刘　宏 (哈尔滨工业大学 机器人研究所, 黑龙江 哈尔滨 150001) 摘　要: 提出一种基于滑模位置控制的模糊自适应阻抗控制策略。 该控制方案通过模糊控制器实时地 调整阻抗参数, 不但可使系统稳定, 而且具有良好的动态品质; 同时内环的滑模位置控制器可增强系统 的鲁棒性。 最后以机器人灵巧手单关节为对象进行仿真研究, 证明了该控制策略的有效性和可行性。 关键词: 阻抗控制; 模糊控制; 滑模控制; 稳定性; 动态品质 中图分类号: T P 24　　　　文献标识码: A Fuzzy Adaptive Im pedance Con trol of D extrous Robot Hand Ba sed on Sl id ing M ode Position Con trol J IA N G L i, CA I H e g ao, L IU H ong (Robo t R esearch In stitu te, H arb in In stitu te of T echno logy, H arb in 150001, Ch ina) Abstract: Fuzzy adap tive im pedance con tro l strategy is p ropo sed based on sliding m ode po sition con tro l. T he con tro l schem e m odifies im pedance param eters real tim e by fuzzy con tro ller so that the stab ility and dynam ic behavio r are im p roved. Sliding m ode po sition con tro ller in inner loop enhances the robu st ness of the system. T he sim u lation study on the jo in t of dex trou s robo t hand show s the validity and fea sib ility of the p ropo sed strategy. Key words: im pedance con tro l; fuzzy con tro l; sliding m ode con tro l; stab ility; dynam ic perfo rm ance 1　引　　言 位置混合控制和阻抗控制[ 1 ]。 与力 　　为使机器人完成与环境相接触的复杂作业, 需 要进行主动柔顺控制, 目前最具代表性的两种控制 策略是力 位置 混合控制相比, 阻抗控制的任务规划量和实时计算 量较少, 并且不需要控制模式的切换, 因而在机器人 柔顺控制中占据着主导地位。 由于商用机器人都配 有高性能的位置控制器, 所以基于位置的阻抗控制 策略得到了广泛的应用[ 2 ]。 　　传统的基于位置的阻抗控制策略, 其目标阻抗 参数 (包括惯量、阻尼和刚度) 在整个控制过程中为 常数。为了保持过渡过程的稳定, 需要较大的阻尼参 数, 但这将导致动态响应的迟缓和较大的冲击力[ 3 ]。 为解决固定阻尼参数不能兼顾稳定性和动态响应的 问题, 目前研究较多的是模型参考自适应阻抗控制。 该方法的缺点是需要在线计算机器人的动力学, 实 时计算量大, 实际应用效果并不理想。 　　本文提出一种模糊自适应阻抗控制策略, 使用 模糊控制器在线调整阻抗参数, 算法简单而有效, 并 　收稿日期: 2000 　作者简介: 姜力 (1971—) , 男, 黑龙江兰西人, 博士生, 从事机器人控制等研究; 蔡鹤皋 (1935—) , 男, 吉林长春人, 教授, 博士 03; 修回日期: 2000 07 10 17 生导师, 中国工程院院士, 从事机电一体化、机器人控制等研究。 © 1994-2010 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net 

Ù Ø Ù Ø Ù Ø Ù Ù Ù Ù Η Η Ø Η Ø Ø 第 16 卷 第 5 期 姜力等: 基于滑模位置控制的机器人灵巧手模糊自适应阻抗控制 613 且可以根据不同阶段的要求, 方便地进行阻抗参数 的局部调整。应用滑模理论设计位置控制器, 实现了 位置控制和阻抗控制的强鲁棒性; 以研制的机器人 灵巧手单关节为对象, 对基于滑模位置控制的模糊 阻抗自适应控制算法进行仿真研究, 证明了该控制 策略的有效性和可行性。 　G (s) = (s) U c (s) = (nK PWM K T )U c (s) - → (n 2J L ) s3 + n 2 (J R + B L ) s2 + 　 　← n 2 (L s + R ) (T f (s) + T g (s) + T L (s) ) 　　 为了进行滑模位置控制器的设计, 在状态空间 中将单关节数学模型写成轨迹误差方程的形式。设 (n 2B R + K eK T ) s (7) 2　数学模型 d ( t) = [ d 　 ¨ d ]T 和 d 　 ( t) = [ 　 ¨ 　 ]T 分别为 2. 1　 机器人灵巧手单关节数学模型 机器人灵巧手单关节是由微型直线驱动器进行 驱动的。直线驱动器是集微型无刷直流电机、高效旋 转直线转换机构和多种感知功能为一体的集成化驱 动器。灵巧手单关节的主要方程如下 (其中参数的含 义和数值见表 1) : 　　 电压平衡方程 U a = R i + L d i d t + e 　　 反电动势方程 e = K ed m d t 　　 电磁转矩方程 　　 转矩平衡方程 T em = K T i (1) (2) (3) T em n = J d2 d t2 + B d d t + T f + T g + T L (4) 　　 减速比方程 n = m (5) 表 1　 机器人灵巧手单关节参数 参数意义 电枢电阻 电枢电感 力矩常数 数 　　 值 R = 5. 7 L = 0. 44 m H K T = 7. 4 × 10- 3 N m A 反电动势常数 K e = 7. 5 × 10- 3 V ( rad s) 折算到关节端的转动惯量 J = 7. 7 × 10- 3 kg m 2 折算到关节端的阻尼系数 B = 5. 2 × 10- 1 Nm ( rad s) 减速比 PWM 常数 电枢电压和电流 关节与环境的作用力矩 重力矩和摩擦力矩 n = 1 218 K PWM = 22 U a, i T L T g , T f 　　 本文使用 PWM 方式调节U a, 从而实现关节的 位置控制。忽略驱动电路的延时, 其传递函数为 U c≈ k PWM 根据上述方程, 可得单关节传递函数为 G PWM (s) = U a (6) 关节的期望轨迹向量和实际轨迹向量, 其中 ¨ d 分别为关节的期望位置, 速度和加速度; 分别为关节的实际位置, 速度和加速度。定义误差向 量为 d 和 ¨ 和 d , , E ( t) = d ( t) - ( t) = [ e1　e2　e3 ]T 则状态空间中的误差方程为 e1 e2 e3 - 0 0 A 3 e 1 e 2 e 3 = 1 0 0 0 1 0 0 A 1 A 2 0 0 A 4 [ T f + T g + T L ] + U c + 0 0 U d (8) 式中 U d = d3 d t3 + d A 1 = - A 2 = - d d2 d t2 + + R L B J n 2B R + K eK T n 2B R + K eK T n 2J L d d d t , 　A 3 = K PWM K T nJ L n 2J L + R L B J , 　A 4 = R J L 2. 2　 目标阻抗模型和环境模型 阻抗控制的实质是调节末端作用力和位置之间 的动力学关系, 目标阻抗模型通常采用二阶线性微 分方程来描述, 即 T L = M t ( ¨ ¨ r - ) + B t ( r - ) + K t ( r - ) (9) 式中,M t, B t 和 K t 分别为目标惯性, 阻尼和刚度, 为关节的参考位置。设 的传递函数为 , 则阻抗控制器 F = r - r G F (s) = T L (s) F (s) = M ts2 + B ts + K t 　　 本文采用刚性环境模型。设 K e 为环境的刚度, 则环境模型方程为 (10) e 为环境的位置, T L = K e ( + e) (11) © 1994-2010 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net 

∃ ÙÞ Þ 3 位置控制内环和阻抗控制外环。根据接触力矩 T L 和 目标阻抗模型 G F (s) , 阻抗控制外环产生位置修正 量 F , 并通过内环的位置控制实现期望的阻抗关 系。文献[ 3 ] 证明了基于位置的阻抗控制的过渡过 程稳定性条件为 t ≥ 0. 5 ( 1 + 2k - 1) t = B t k = K e (2 K t K tM t) 1 (21) 　 　由式 ( 21) 可以看出, 为了实现过渡过程的稳 定, 目标刚度应远小于环境刚度, 同时目标阻尼要足 够大。理论和实验证明, 高阻尼有利于过渡过程的稳 定, 但同时会导致动态响应的迟缓和冲击力的增大。 为了解决这一问题, 本文在基本阻抗控制方案的基 础上, 根据不同阶段对阻抗参数的不同要求, 应用模 糊规则实时调整阻抗参数, 在减小冲击力的同时, 保 证了过渡过程的稳定性。 4. 2　 基于滑模位置控制的模糊自适应阻抗控制[ 3 ] 基于滑模位置控制的模糊自适应阻抗控制策略 的目标是: 1) 增强过渡过程中关键阶段的稳定性; 2) 改善过渡过程的力响应 (减小冲击和力超调) ; 3) 达到静态期望力, 且不依赖于环境参数。控制器结构 如图 1 所示, 它由 3 部分组成: 1) 内环的滑模位置控 制器; 2) 外环的阻抗控制器; 3) 模糊自适应机构, 它 根据力响应在线计算并调整阻抗参数。 图 1　 基于滑模位置控制的模糊自适应阻抗控制器结构 模 糊 控 制 器 有 两 个 输 入 变 量: 1) 力 偏 差 , 其中 T d 为 signT L (k ) devT (k ) = (T d - T L (k ) ) 为接触标志函数, 用以 期望的静态力, signT L (k ) 判 断与环境是否相接触, 在自由空间中devT (k ) = 0; 2) 力增量 T (k ) = T L (k ) - T L (k - 1)。模糊控 制器有一个输出变量 B t, 它是目标阻尼参数的修 正量。 　 　为方便模糊控制器的设计, 将两个输入变量和 一个输出变量进行归一化处理, 即 　　　devT (22) 614 控 　　 制 　　 与 　　 决 　　 策 2 0 0 1 年 3　 滑模位置控制器的设计[ 4, 5 ] 　　 基于位置的阻抗控制要求内环的位置控制器 具有很强的鲁棒性和快速的动态响应。本文应用滑 模变结构理论设计关节位置控制器, 其设计由两部 分组成: 1) 求切换函数 s (E ) , 使系统的滑动模态渐 近稳定并具有所要求的动态品质; 2) 求控制函数 U c (E ) , 使滑模的存在条件和到达条件得以满足。 3. 1　 切换函数 s (E ) 的选择 采用线性切换函数 s (E ) = C E ( t) (12) 式中, C = [ c1　c2　c3 ], E ( t) = [ e1　e2　e3 ]T , 取 c3 = 1。系统的滑模运动方程为 1 + c2e 方程 (13) 的特征方程为 e 1 + c1e1 = 0 (13) p 2 + c2p + c1 = 0 (14) 为保证系统渐近稳定, 要求 c1 > 0, c2 > 0; 为保证系 统无超调, 要求 c2 3. 2　 控制函数U c (E ) 的选择 2 ≥ 4c1。 所采用的控制函数为 1 和 2e2 + 1e1 + sgn (s) U c = 2 分别为 e1 和 e2 的反馈增益, (15) 式中, 是一个小 的正数, 它可保证原点处 (e1 = e2 = e3 = 0) 满足滑 模存在条件, 并且提高系统的抗干扰能力, 消除静态 误差。 　　 根据广义滑模条件可以得到 3) s = 1 + c2e = (c1e c1c2 - c2 2 - 2 + e c1A 2 - A 3 c2A 2 - A 3 ss (- A 2 - (c2 + A 2) s2 + [A 4 (T L + T g + sgn (s) s < 0 T f ) + U d ]s - A 3 1) e1s + (c1 + 2) e2s + 通过逐项优超的方法满足上式, 得到 1 = 2 = 1, 　e1s > 0 1, 　e1s < 0 2, 　e2s > 0 2, 　e2s < 0 c2 < - A 2 = B J + R L > (A 4 (T L + T g + T f ) + U d ) A 3 (16) (17) (18) (19) (20) 4　 基于滑模位置控制的模糊自适应 阻抗控制 4. 1　 阻抗参数恒定的阻抗控制 基于位置的阻抗控制方案由两个控制环组成: m ax © 1994-2010 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net (k ) = devT (k ) devT 

第 16 卷 第 5 期 姜力等: 基于滑模位置控制的机器人灵巧手模糊自适应阻抗控制 615 T T B B m ax m ax (k ) = (k ) = T (k ) B (k ) 　　　 (23) 　　　 (24) 　　 将所有的输入输出变量划分为 7 个模糊子集, 分别用语言值 NB , NM , N S, ZO , PS, PM 和 PB 表 示。每个模糊集的隶属度函数均选为高斯基函数。模 糊控制规则表略。 　　 模糊推理采用传统的M am dan i 算法, 模糊推理 规则采用m ax m in 复合运算, 即 C ( i (devT A (k ) ) ) ∧ 49 (y ) = ∨ i ( i= 1 B (25) 模糊推理结果的非模糊化采用重力中心法 (CO G) , 输出结果为 i (y ) (k ) ) ∧ T C B t (k ) = ∫ C (y ) y dy ∫ C (y ) dy (26) 目标阻抗参数的初始值按式 (21) 选择。当关节与环 境接触后, 模糊控制器产生 B t, 对目标阻尼进行实 时调节, 在最大冲击以前采用较小的目标阻尼以减 小力超调, 而最大冲击以后采用较大的阻尼以保证 接触的稳定性。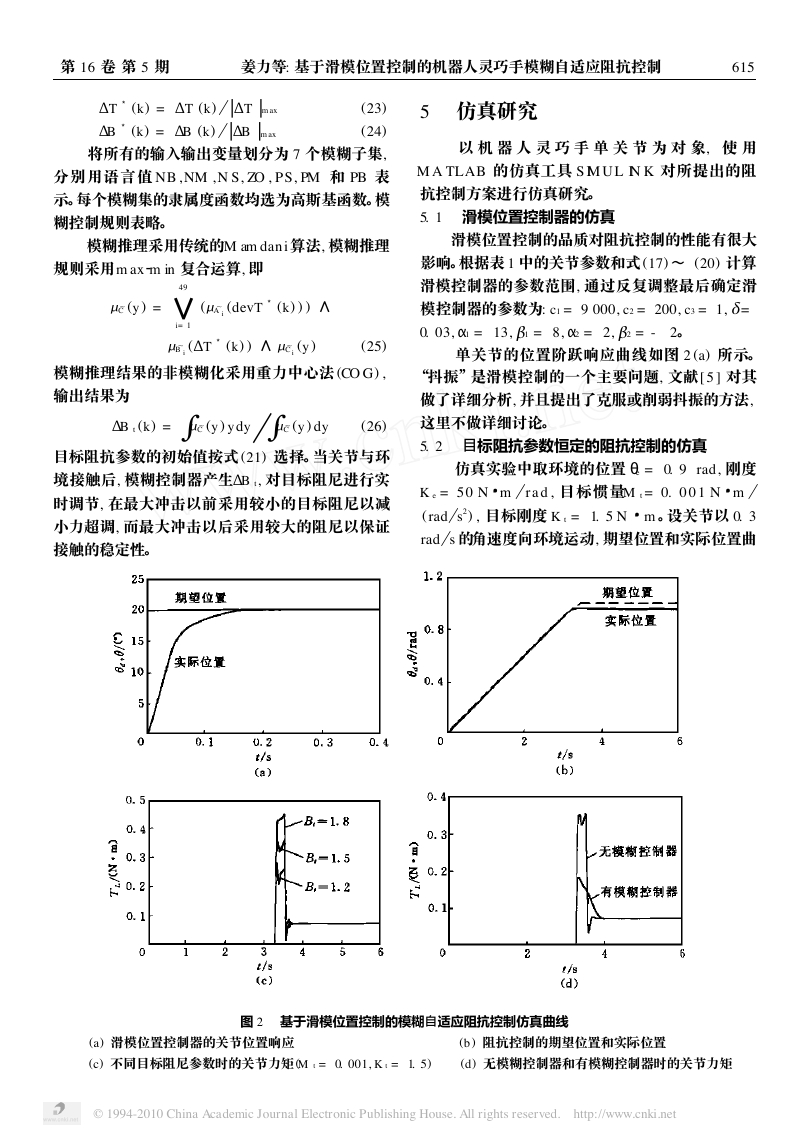 5　 仿真研究 　　 以 机 器 人 灵 巧 手 单 关 节 为 对 象, 使 用 M A TLAB 的仿真工具 S IM U L IN K 对所提出的阻 抗控制方案进行仿真研究。 5. 1　 滑模位置控制器的仿真 2 = 2, 1 = 8, 1 = 13, 2 = - 2。 滑模位置控制的品质对阻抗控制的性能有很大 影响。根据表 1 中的关节参数和式 (17) ～ (20) 计算 滑模控制器的参数范围, 通过反复调整最后确定滑 模控制器的参数为: c1 = 9 000, c2 = 200, c3 = 1, = 0. 03, 　　 单关节的位置阶跃响应曲线如图 2 (a) 所示。 “抖振”是滑模控制的一个主要问题, 文献[ 5 ] 对其 做了详细分析, 并且提出了克服或削弱抖振的方法, 这里不做详细讨论。 5. 2　 目标阻抗参数恒定的阻抗控制的仿真 　　 仿真实验中取环境的位置 K e = 5 0 N (rad rad m。设关节以 0. 3 s2) , 目标刚度 K t = 1. 5 N s 的角速度向环境运动, 期望位置和实际位置曲 r a d , 目标惯量M t = 0. 0 0 1 N e = 0. 9 rad, 刚度 m m 图 2　 基于滑模位置控制的模糊自适应阻抗控制仿真曲线 　　 (a) 滑模位置控制器的关节位置响应 　　　　　　　　 　　 (b ) 阻抗控制的期望位置和实际位置 　　 (c) 不同目标阻尼参数时的关节力矩 (M t = 0. 001, K t = 1. 5) 　 (d) 无模糊控制器和有模糊控制器时的关节力矩 © 1994-2010 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net 

2 2 2 2 2 2 2 2 2 616 控　　制　　与　　决　　策 2 0 0 1 年 线如图 2 (b) 所示。使用不同的目标阻尼B t 所得的一 组力矩响应曲线如图 2 (c) 所示。可以看出, 在采用 相同M t 和 K t 的情况下, 随着B t 的增加, 冲击力和力 超调变大, 但是冲击之后力的振荡幅度减小, 即接触 稳定性提高, 证明了实时调整阻尼参数的必要性。 5. 3　 模糊自适应阻抗控制的仿真 超调减小。以机器人灵巧手单关节为对象, 建立了仿 真对象及控制器的数学模型, 给出了滑模位置控制 器和模糊控制器的设计过程。仿真研究结果表明, 该 控制策略对于控制性能的提高有明显的作用, 是一 种有效而可行的控制方案。 m (rad 采 用与 5. 2 节相同的仿真条件, 初始目标阻尼 B t0 选为 1. 5 N s) , 采用模糊自适应阻抗控 制算法进行仿真研究, 得到的力矩响应曲线如图 2 (d) 所示。与图 2 (c) 相比, 力矩的超调明显减小, 同 时接触稳定性也有所增强, 从而较好地解决了采用 恒定阻抗参数的阻抗控制所存在的问题。 6　 结 　 　语 　　目标阻抗参数恒定的基于位置的阻抗控制, 过 渡过程的稳定性和动态品质不能同时得到提高。 针 对这一缺点, 本文提出一种基于滑模位置控制的模 糊自适应阻抗控制策略。使用滑模位置控制内环, 可 以有效地增强系统的鲁棒性; 使用模糊控制器在线 调整目标阻尼参数, 既可保证接触的稳定, 又可使力 　　 (上接第 611 页) 5　结　　论 　　1) 输出反馈的鲁棒性能设计包括两方面内容, 即输入 (端) 扰动的抑制和输出 (端) 灵敏度问题。 本 文主要讨论输出灵敏度问题。 由于参数不确定性系 统输出反馈的解 (式 (8) ) 不是线性不等式, 所以应求 解式 (9) , 即先求解一个输出注入问题。 输出注入问 题中的最优性能 是灵敏度问题的性能极限, 所以 这种分步求解的做法, 其物理概念比较清楚。 　　2) 本文为说明基本方法, 在算例中未加进权函 数。对于实际设计问题而言, 应在对象中加上与性能 要求有关的权函数。 参考文献: [1 ] X ie L , FU M , Carlo s E D e Soaza. H ∞ con tro l and quadratic stab ilization of system s w ith param eter un certain ty via ou tpu t feedback [J ]. IEEE T ran s on A u tom Con tr, 1992, 37 (8) : 1253 1256. [ 2 ] Yamm ada Y, H ara S. Global op tim ization fo r H ∞ con IEEE T ran s on tro l w ith con stan t diagonal scaling [J ]. 参考文献: [ 1 ] Hogan N. Im pedance con tro l: A n app roach to m an ipu lation [J ]. J D yn Syst M eas Con tr, 1985, 107 (1) : 1 24. [ 2 ] D rago ljub Su rdilovic. Syn thesis of im pedance con tro l law s at h igher con tro l levels: A lgo rithm s and experi m en ts[A ]. P roc of IEEE In t Conf on Robo tics and A u tom ation [C ]. L euven, 1998. 213 218. [ 3 ] D rago ljub Su rdilovic. Robu st robo t com p lian t m o tion con tro l u sing in telligen t adap tive im pedance app roach [A ]. P roc of IEEE In t Conf on Robo tics and A u tom a tion [C ]. M ich igan, 1999. 2128 2133. [ 4 ] H L iu, J B u tterfass, S Knoch et a l. A new con tro l strategy fo r DL R ′s m u ltisen so ry articu lated hand [J ]. IEEE T ran s on Con tr Syst, 1999, 19 (2) : 47 54. [ 5 ] 高为炳. 变结构控制理论基础[M ]. 北京: 中国科学技术 出版社, 1990. A u tom Con tr, 1998, 43 (2) : 191 202. [ 3 ] Jabbari F. O u tpu t feedback con tro ller fo r system s w ith IEEE T ran s on A u tom Con structu red uncertain ty[J ]. tr, 1997, 42 (5) : 715 719. [ 4 ] Iw asak i T , Skelton R E. A ll con tro llers fo r the general H ∞ con tro l p rob lem : LM I ex istence condition s and state space fo rm u las [ J ]. A u tom atica, 1994, 30 ( 8 ) : 1307 1317. [ 5 ] Doyle J C, Glover K, Khargonekar P P et a l. State space so lu tion s to standard H 2 and H ∞ con tro l p rob IEEE T ran s on A u tom Con tr, 1989, 34 (8) : lem s [J ]. 831 847. [ 6 ] Zhou K, Khagonekar P P, Stou strup J. Robu st perfo r m ance of system w ith structu red uncertain ties in state space [J ]. A u tom atica, 1995, 31 (2) : 249 255. [ 7 ] Schm itendo rf W E. D esign m ethodo logy fo r robu st sta b ilizing con tro llers[J ]. A IAA J Gu id Con tr D yn, 1987, 10 (3) : 250 254. [ 8 ] Gah inet P, N em irovsk i A , L aub A J et a l. LM I con tro l too lbox [M ]. N atick: T he M ath W o rk s Inc, 1995. © 1994-2010 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net