湖北武汉小升初招生考试数学真题.doc-资料库

第1页 / 共8页

第2页 / 共8页

第3页 / 共8页

第4页 / 共8页

第5页 / 共8页

第6页 / 共8页

第7页 / 共8页

第8页 / 共8页

湖北武汉小升初招生考试数学真题第一套一、脱式计算。 1、 (1 1 2  1 3 )  ( 1 4  1 1 2  1 2.2 1 ) 5  2、 15.37 7.89 9.37 7.89 15.37 2.11 9.37 2.11        3、 1 1 1 3 3 5     1 5 7     1  2001 2003  1  2003 2005 4、 2222  29 100  3333 0.04 6666 0.09    二、填空题。 5、找出规律，在横线上填数。 2，4，，8，6，，8，16，10，20。 6、如果将一根木料锯成 3 段，小华要用 6 分钟，王叔叔锯木料的速度是小华的 3 倍，由王叔叔把这根木料锯成 6 段，需要分钟。 7、一颗流星飞行 3 秒就消失了，第一秒飞行 8.8 千米，以后每秒都比前一秒多飞行 12.2 千米，这颗流星飞行了千米。 8、一根绳子围着大树如果绕 10 圈剩 3 米，如果绕 11 圈又缺 1 米，那么绕 8 圈剩米。 9、小红买了三支铅笔和一块橡皮，小敏买了一支铅笔和三块橡皮，她们用的钱数之比是 3：2，一支铅笔是 7 角钱，那么一块橡皮是角钱。

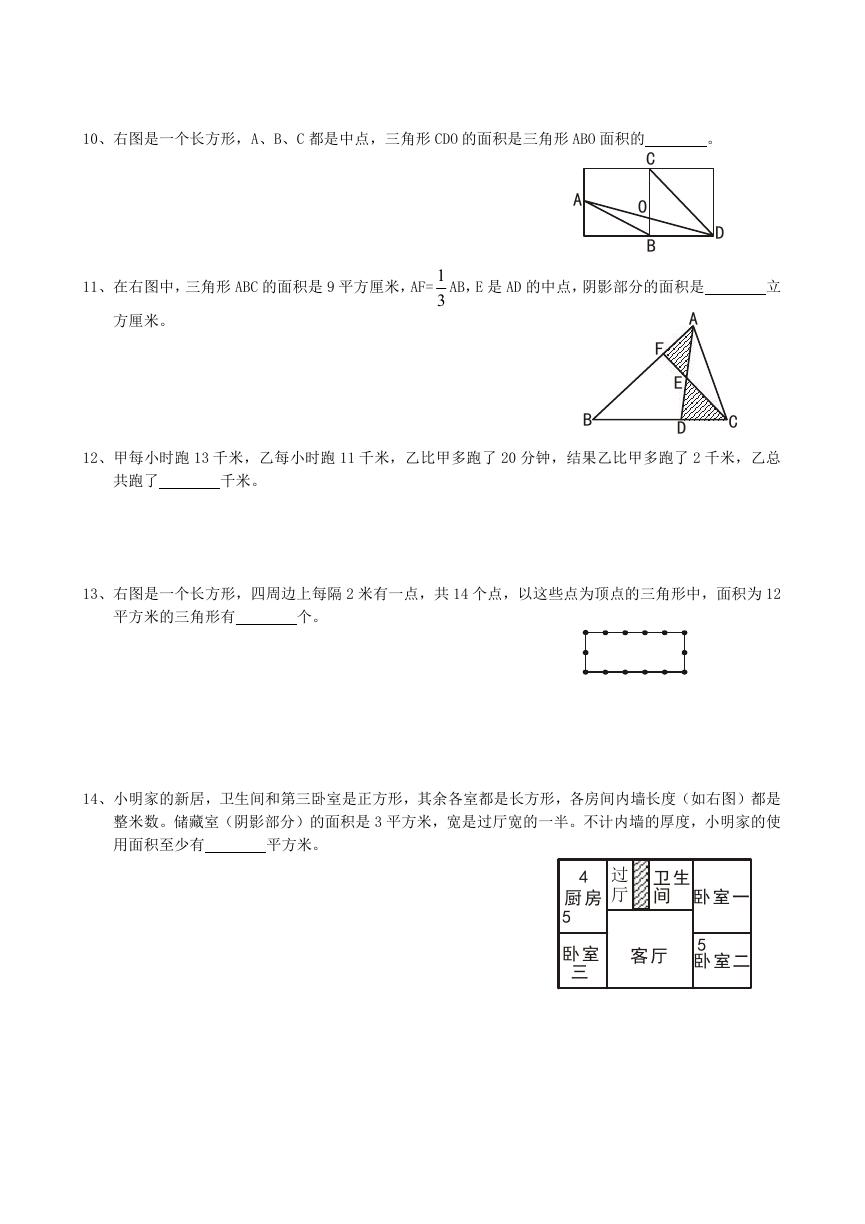
10、右图是一个长方形，A、B、C 都是中点，三角形 CDO 的面积是三角形 ABO 面积的。 11、在右图中，三角形 ABC 的面积是 9 平方厘米，AF= 方厘米。 1 3 A C O B D AB，E 是 AD 的中点，阴影部分的面积是立 A F E D C B 12、甲每小时跑 13 千米，乙每小时跑 11 千米，乙比甲多跑了 20 分钟，结果乙比甲多跑了 2 千米，乙总共跑了千米。 13、右图是一个长方形，四周边上每隔 2 米有一点，共 14 个点，以这些点为顶点的三角形中，面积为 12 平方米的三角形有个。 14、小明家的新居，卫生间和第三卧室是正方形，其余各室都是长方形，各房间内墙长度（如右图）都是整米数。储藏室（阴影部分）的面积是 3 平方米，宽是过厅宽的一半。不计内墙的厚度，小明家的使用面积至少有平方米。 4 厨房 5 卧室三过厅卫生间卧室一客厅 5 卧室二

三、几何计算。 15、已知三角形 EBC 的面积是 73.5 2cm ，AD=9 ㎝，BC=21 ㎝，求阴影部分的面积。 A E D B C 16、下图中，平行四边形 ABCD 的边 BC 长 10 厘米，直角三角形 BCE 的直角边 EC 长 8 厘米，已知阴影部分的面积比三角形 EFG 的面积大 10 平方厘米，求 EF 的长。四、应用题。 17、甲、乙合作完成一项工作，由于配合得好，甲的工作效率比单独做时提高了 A G B D E F C 1 10 ，乙的工作效率比单独做时提高了 1 5 需要多少小时？，甲、乙合作 6 小时完成了这项工作。如果甲单独做需要 11 个小时，那么乙单独做 18、小明通常总是步行上学，有一天他想锻炼身体，前 1 3 路程快跑，速度是步行速度的 4 倍，后一段路程慢跑，速度是步行速度的 2 倍。这样，小明比平时早 35 分到校，小明步行上学需要多少分钟？ 19、甲、乙两人进行射击比赛，约定每中一发记 8 分，脱靶一发倒扣 3 分。两人各打 10 发，共得 116 分，其中甲比乙多得 22 分。甲、乙两人各中多少发？

五、实践与操作。 20、某工厂原用长 4 米，宽 1 米的铁皮围成一个没有底和顶的棱长为 1 米正方体形状的产品临时存放处，恰好能存放一周的产品，现在该产品产量增加了。（1）请设计一种方案使之能用原来的铁皮围成一个容器（无底、无顶）装下现在一周的产品？（2）设计的容器最大容量时，一周的产品增加的百分数。第二套一、判断题。（对的括号里写 A，错的括号内写 B） 1、（）一个整数能被另两个整数整除，那么它也能被这两个数整除。 2、（）两数相乘，乘数大于 1 时，积大于被乘数。 3、（）周长等于 1 厘米的半圆所在圆的周长是 2 厘米。 4、（）一项工程，甲单独做要 1 2 小时，乙单独做要 1 3 小时，两人合做要 5 6 小时完成。 5、（）如果一个整数末三位与去掉末三位所得整数的差是 7 或 13 的倍数，那么原数也是 7 或 13 的倍数。 6、（）所有分母里含有 2 和 5 以外质因数的最简分数都不能化成有限小数。二、选择题。 7、 5.79 保留两位小数是（） A．5.79 B．5.7 C．5.8 D．5.80 8、女生人数占全班人数，则男生与女生人数的比是（） 5 11 B．5:6 A．6:5 C．6:11 D．5:11 9、下列叙述的数或式中，不变的有（）（1）一个数乘以 0.9 的积。（2）分子和分母同时乘以或除以同一个数的分数。（3）前项和后项同时乘以或除以 2 的比例。（4）几个数的和除以 2 的商与这几个数分别除以 2 的商的和。 A．1 个 B．2 个 C．3 个 D．4 个 10、把一个棱长 2 分米的正方体削成一个最大的圆柱体，那么正文体的表面积 a 与圆柱体的表面积 b 的关系是（） A．a＞b B．a=b C．a＜b D．无法比较 11、两数的最大公约数与最小公倍数的和是 106，而这两个数的和不唯一，这个和的不同值有（） A．3 个 B．4 个 C．5 个 D．6 个 12、一次植树活动，六（三）班每人平均栽树 1.11 棵，后来发现少统计了 9 棵树，加上这 9 棵树树后，

每人平均栽树 1.32 棵（以上两个平均数都是由四舍五入到 0.01 的近似数），那么六（三）班参加植树的人数是（） A．45 C．43 B．44 D．42 三、填空题。 13、用小数表示：八分之三为元。；三十万三十点三为；四元钱打三五折的二五成是 14、111 的质因数连乘积是；约数是。 15、a 是 b 的 4 7 ，b 是 c 的 3 8 ，a 是 c 的。 16、4x－5=6 的解能使 7x－8 的值等于。 17、在比例尺为 1：1000 的地图上面积是 1 平方厘米的圆的实际面积是平方米。 18、一月有四个星期一和四个星期五，这年的元旦是星期。 19、某人带的钱恰好可买 8 千克肉或 20 千克米或 30 千克菜。他用这些钱买了相同千克数的肉和米和菜。这个相同千克数是。 20、写出小于 20 的所有的三个正整数，使它们的最大公约数是 1，且两两均不互质。 21、一个两位数，十位数乘 3，个位数减去 3，所得的两位数比原两位数的 4 倍少 45；十位数减去 2，个位数乘 2，所得的两位数比原两位数一半大 1。这个两位数是。 22、第一个数乘以 8 15 的积加上 203 得第二个数，第二个数乘以 8 15 的积加上 203 得第三个数，第三个数乘 8 15 以是的积加上 203 得第四个数，这样一直下去，得到的第 2003 个数与第 23 个数相等，则这个数。四、计算题。 23、37.6 4.87 8.3 1.13    24、 1 63  ( 2 3    2 7 1 9 4 21 )

25、 31 5 19  (7 11 12  5 7 15  6 3 5  3 1 2  11 25 )  1 (3.125 3 ) 8  26、 2 22 665  2 89 209  1 617 748 五、应用题。 27、杨树和柳树共 60 棵，杨树的和柳树的共 26 棵，求柳树有多少棵？ 28、某次竞赛，红旗中学参赛的男生人均分为 92 分，女生人均分 86 分，全体参赛学生人均分为 90 分，且已知参赛的男生人数比女生人数多 20 人。求红旗中学共有多少人参赛？ 29、甲、乙两马车分别从 A、B 两地同时相向而行，且各按匀速前进。甲车从 A 到 B 要行驶 45 小时，乙车从 B 到 A 要行驶 35 小时。但甲车每行 5 小时要停下用 1 小时喂马，乙车每行 7 小时要停下用 2 小时喂马。求两车相遇时，乙车行驶了全程的几分之几？ 30、如图，在四边形 ABCD 中，角 A 和角 C 是直角，CD=CB，求 AC=1 厘米时，四边形 ABCD 的面积。

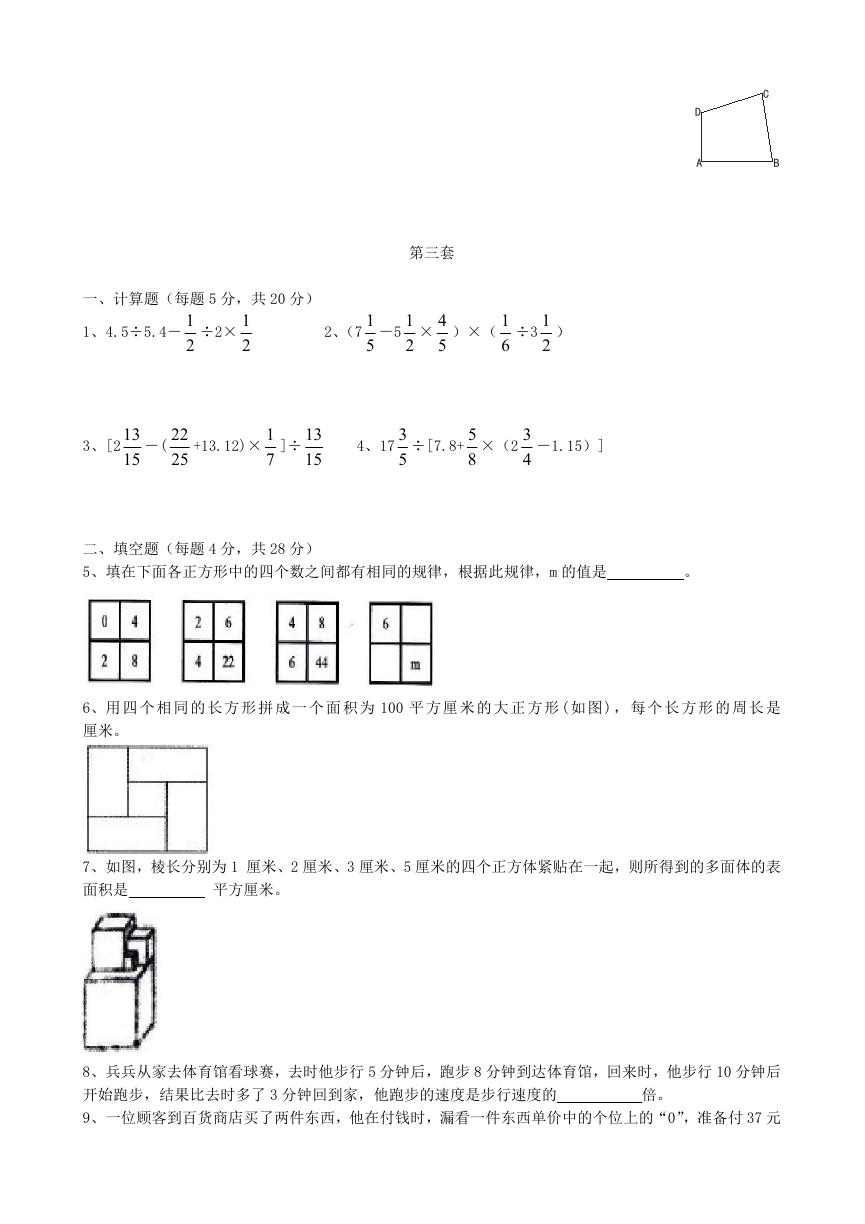
D A C B 第三套一、计算题（每题 5 分，共 20 分） 1、4.5÷5.4－ 1 2 ÷2× 1 2 2、（7 1 5 －5 1 2 × 4 5 ）×（ 1 6 ÷3 1 2 ） 3、[2 13 15 －( 22 25 +13.12)× 1 7 ]÷ 13 15 4、17 3 5 ÷[7.8+ 5 8 ×（2 3 4 －1.15）] 二、填空题（每题 4 分，共 28 分） 5、填在下面各正方形中的四个数之间都有相同的规律，根据此规律，m 的值是。 6、用四个相同的长方形拼成一个面积为 100 平方厘米的大正方形 ( 如图 ) ，每个长方形的周长是厘米。 7、如图，棱长分别为 1 厘米、2 厘米、3 厘米、5 厘米的四个正方体紧贴在一起，则所得到的多面体的表面积是平方厘米。 8、兵兵从家去体育馆看球赛，去时他步行 5 分钟后，跑步 8 分钟到达体育馆，回来时，他步行 10 分钟后开始跑步，结果比去时多了 3 分钟回到家，他跑步的速度是步行速度的 9、一位顾客到百货商店买了两件东西，他在付钱时，漏看一件东西单价中的个位上的“0”，准备付 37 元倍。

取货，售货员说:“您看错了单价，应该付 91 元才对。”请你算一算，这两件东西的单价差是少元。多 10、某矿山有石头，第一次运走它的 1/2,第二次运走剩下的 1/3,第一次又运走剩下的 1/4,.......,照这样计算，运走 500 次后，还剩 1 吨石头，这批石头原有吨。 11、如图所示的三条圆形跑道，每条跑道的长都是 0.5 千米，A，B，C 三位运动员同时从交点 O 出发。分别沿三条跑道散步，他们的速度分别是每小时 4 干米、每小时 8 千米、每小时 6 千米，问：从出发到三人第一次相遇，他们共走了千米。三、解答题（12—15 每题 10 分，16 题 12 分，共 52 分） 13.两个相同的直角三角形如图所示(单位:厘米)重叠在一起，求阴影部分的面积? 14.甲乙两人分别从 A. B 两地同时同向而行，经过 4 小时，甲在 C 处追上乙，这时两人共行 78 千米，乙从 A 到 B 要行 1 小时 45 分，求 A, B 两地相距多少千米? 15.蜘蛛有 8 条腿，蜻蜓有 6 条腿和 2 对翅膀，蝉有 6 条腿和 1 对翅膀，现在这三种小虫共 18 只，有 118 条腿和 20 对翅膀，问每种小虫各几只? 16.把从 1 开始的奇数按如下规律排列起来: (第 1 行) 1; (第 2 行) 3，5; (第 3 行) 7，9， 11; ······ （1）前面 9 行共有（2）2013 是第（3）求前面 100 行所有数的和。个数; 行第个数;

资料库

湖北武汉小升初招生考试数学真题.doc

相关推荐

小升初

热门标签

最新资料