第34卷增刊 2008年1 2月 光学技术 OPTICAL TECHNIQUE V01．34 Suppl． I)ec．2008 文章编号：1002—1582(2008)S-0181．03 三角调频连续波建模与数值仿真+ 栗苹1，郭渭荣1，田力2，陈慧敏1，李月琴1 (1．北京理工大学宇航科学技术学院，北京100081；2．防灾科技学院灾害信息工程系，河北三河065201) 摘要：三角调频连续波由于测距精度高，所以在测距系统中有着广泛的应用。结合模数晒数、绝对值函数和符号 函数，推导了三角调频连续波的频率和相位的数学表达式，并进行了建模及仿真。仿真结果表明，频率和相位的数学表 达式满足微积分的关系，能够描述三角波调频在跨越调频周期时的不连续性。 关键词：调频连续波；三角波调频；频率；相位 中图分类号：TH744 文献标识码：A Modeling and numerieal simulation of triangle FMCW LI Pin91，GUO Wei—ron91，TIAN Li2，CHEN Hui-minl，LI Yue—qinl (1．School of Aerospace Science and Engineering，Beijing Institute of 7Fechnology，Beijing 100081，China) (2．Department of Disaster Information Engineering，Institute of Dis&ster Prevention Science and Technology，Hebei Sanhe 065201，China) Abstract：Triangle FMC3V is widely used in ranging systmas for its high ranging precision．Considering features of modulo function，aKsolute value function and sign function，analytical expression of frequency and phase of triangle FMCW is given． Modeling and simulations are realized．Rmult of simulation shows that frequency and phase expressions have relationship of dif— ferential and integral．The expre赋sions can correctly describe the discontinuousness of triangle FM(TW at boundary between FM periods． ， Key words：FMCW；triangle FM；frequency；ph碰se 1 引 言 近年来，调频连续波被广泛地应用于测距系统。由于调 其中t为时间，9(t)为t时刻的瞬时相位，f(t)为t时刻的瞬 时频率，妒。为0时刻的瞬时相位。式(1)和式(2)表明，调频 连续波频率与相位的微分成正比，而相位与频率的积分成正 频连续波测距是依靠发射信号和接收信号之IhJ的频率差进行 比。 距离测量的，与信号幅度关系不大，这在很人程度上降低了测 用不同的调制方式对频率进行调制，即可产生具有不同 距系统对测量环境和被测物体反射率的要求，使得系统具有 时频关系曲线的调频连续波。常用的调频连续波的调制方式 更高的抗干扰性和测距精度…1。 有正弦波调频、锯齿波调频和二三角波调频，根据三角波凋频方 三角调频连续波的波形在跨越调频周期时具有不连续性 式产生的连续波信号的时频变化规律如图1所示。 的特点，目前并没有明确的数学模型对其进行描述，给调频连 续波的应用和研究带来一定的困难。本论文通过引入模数函 3三角调频连续波的数学表达式 数、绝对值函数和符号函数，建立了相应的数学表达式，并对 3．1频率和相位表达式 其进行了解析验证和数值仿真。 2调频连续波的特点及分类 调频连续波是指频 率随时闯按调制信号规律 变化的波形，瞬时频率和 瞬时相位相互之间具有微 分和积分的关系【2】： f(t)=麦措(1) 厶儿 U、‘， 驴(t)=27cIf(r)dr+妒。 } 奄 (2) 三角调频是指频率按周期性三角形波的规律变化的，产 生一种线性频率调制信号，其频率在前半个周期中随时间线 性增加，而在后半个周期中随时间线性减dd3J。 为了描述跨越调频周期的不连续的频率变化和相位变 化，引入具有不连续性的模数函数、绝对值函数和符号函数， 并提出能够描述跨越凋频周期的不连续情况下的三角调频频 率表达式和相位表达式： f(t，=如+厶×{丢一幽[2型号趔一，]} (3) ／翌!1 2二逝＼ ， ＼ 2矗 =(^+每)∽u一等嘶(型号掣一，)· 图1三角调频的 频率变化示意图 _收稿日期：20(18．08—26 E-mail：variable@bit．edu．cn 作者简介：栗苹(1966．)，女，河北省人，北京理工大学字航科学技术学院教授，博士，主要从事信息感知与信息对抗方面的研究。 181 ˝ • ‰ ˚ 

光学技术 (型≮训一-)2一 鲁((t一¨一函(t一‰u)+等一1) (4) 其中fo为中心频率，厶为频率调制范围的大小，t。为调频周 期，to为初始时刻，90为初始时刻的相位。 图2模数函数示意图 图3求绝对值函数示意图 l厂————1===习 mod是模数函数， mod(7n，以)给出优除以0．6} 刀后的余数。abs是求绝对贫0．2} 值函数，abs(z)给出实数．萝-o．2} ．0．6l 或复数的绝对值，sign是 求符号函数，sign(x)当z ．1L==一． 为负数、零或正数时分别 给出，1、o警．1 o．粤．2孳 mM(z，2)所对应的曲 ～。1 ‘5 ·3 图4求符号函数示意图 { { | { j 5 3 线。图3是abs(z)的曲线，图4是sign(x)的曲线。从图2可见， 模数函数的曲线呈锯齿形，在一个周期内增长，在跨越周期时 不连续地跳变回起始的位置。式(3)通过使模数函数除以t， 产生出周期为t。的锯齿，再通过绝对值函数使波形的斜率发 生转折，形成三角形波，乘以厶后，变化范围大小为厶。为描 述作为频率积分的相位的变化，在式(4)的相位表达式中加入 模数函数的平方项。但式(3)的频率表达式与式(4)的相位表 达式是否满足式(1)和式(2)的微积分的关系还需要进一步验 证。 3．2相位表达式的微分 模数函数、绝对值函数和符号函数具有如下的性质【4，5】： 凼号争业：1，z≠缈，五：0，±1，±2，…(5) (6) abs(x)=sign(x)x 煎掣：0，z≠0 (7) (8) 区i尘望(兰)2一建i茧融(兰)星2 一 如 妇 =zd—(sigin_(x))+sign(z)盘dx =sign(x)。z≠0 对式(4)的相位表达式进行微分： 2丁c 』陋!1 2二翌Q＼ ， d￡＼ =(，o+譬)一警啦(型掣一·)× 2(型≮逍一，)蔷(型≮州一t) =(，o+鲁)一厶如(婴掣一t) =如+厶×户(号一抵(婴掣一t))(9) 182 第34卷 这样就证明了式(4)的相位表达式的微分在间断点之外 等于式(3)的频率表达式，式(3)和式(4)满足式(1)的微分关 系。如果能证明式(4)的相位表达式在间断点上等于式(3)的 频率表达式的积分，就能进一步确定式(3)与式(4)问的微积 分关系。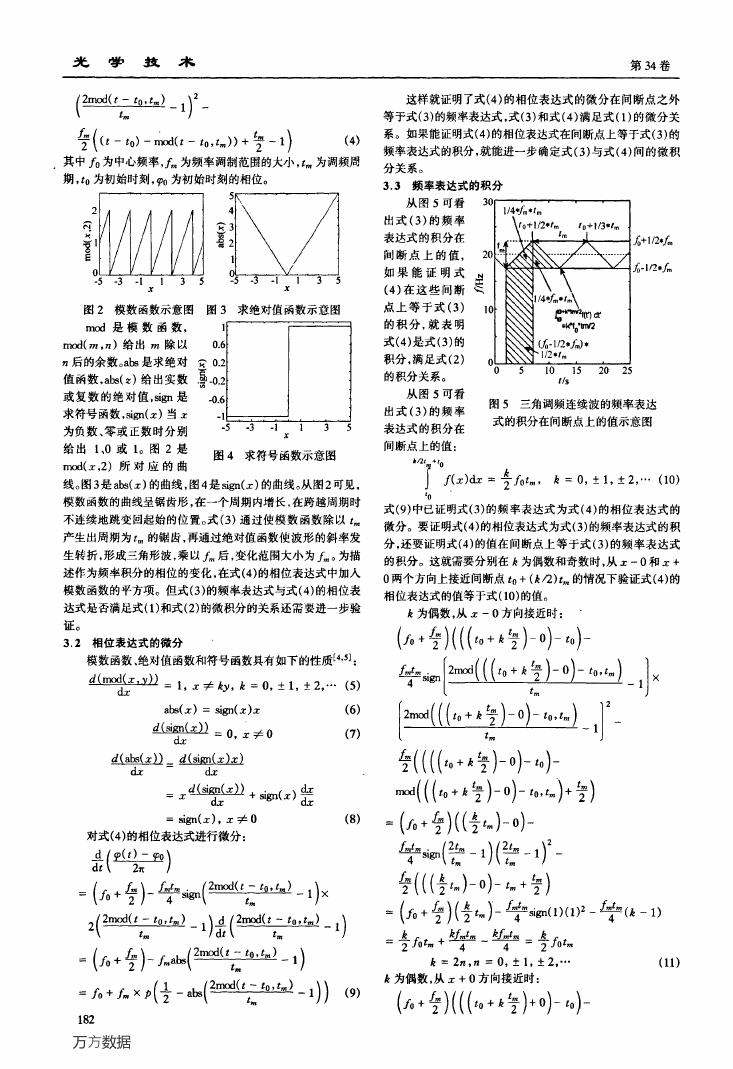 3．3频率表达式的积分 从图5可看 30 出式(3)的频率 表达式的积分在 间断点上的值， 20 1／4*fm*tm ，o十l／2·，m J：：+l，2机 fo—I／2．五 星 如果能证明式 (4)在这些间断 点上等于式(3) 的积分，就表明 式(4)是式(3)的 积分，满足式(2) 的积分关系。 从图5可看 出式(3)的频率 表达式的积分在 间断点上的值： l／4*fm*t。l脚r)删 埘’；trot2 “-1／2,朋· 、l／2·f。 0 O 5 10 15 20 25 t／s 图5三角调频连续波的频率表达 式的积分在间断点上的值示意图 “‘m’‘0 j『f tO f(x)如z号^‰忌=o，±1，±2，…(10) 式(9)中已证明式(3)的频率表达式为式(4)的相位表达式的 微分。要证明式(4)的相位表达式为式(3)的频率表达式的积 分，还要证明式(4)的值在间断点上等于式(3)的频率表达式 的积分。这就需要分别在忌为偶数和奇数时，从z一0和z+ 0两个方向上接近间断点to+(量／2)t。的情况下验证式(4)的 相位表达式的值等于式(10)的值。 k为偶数，从z一0方向接近时： 。 J L ￡研 (如+鲁)(((”矗等)一o)咱)一 等si舭f型业擘止止生，1× 怛监：型二!b生，1 2一 夸((((”忌每)一o)咄)一 删(((”五等)一o)嘶，t。)+等) =(，o+拿)((专t。)一o)一 f"h，tSsign‰一-)f＼地tm一-)2一 夸(((寺t。)一o)一t。+等) =(如+譬)(专‰)一等sign(1)(D2一警(屉一1) =寺^t。+笪净一型净=寺，0r。 七=2n，挖=0，±1，±2，… (11) 忌为偶数，从z+0方向接近时： (^+譬)(((z。+矗每)+o)一t。)一 ˝ • ‰ ˚ 

增刊 等嘶[型睑掣一。]× 【 f坍 ‘J 脚＆李斟2垒U 2一 争((((”志等)+o)嘶)一 删(((”惫等)+o)嘞，靠)+等) =(如+譬)((知)+0)一 峥si印(掣一-)(掣一·)2- 譬(((寺t。)+o)一o+乎) =专^t。+笪予+等一堑乎(愚+1)=寺如如 k=2n，挖=0，±1，±2，… (12) 忌为奇数，从z一0方向接近时： (^+夸)(((”惫等)一o)嘶)一 警si即f型业墨划一。卜 f!!啦!：!盐生■一，]2一 夸((((”志每)一o)咱)一 删(((”矗誓)一o)飞^)+乎) =(兀+譬)((是每)一o)一 簪叫掣一。][掣一。]2一 鲁(((忌每)一o)一((等)一o)+每) =(，o+譬)(量等)一等(七一·+，)=专厶t。 k=2n+1，行=0，±1，±2，… (13) 惫为奇数，从z+0方向接近时： (^+譬)(((”忌每)+0)咱)一 等si鲫f型业≤出生■一。1× f竺啦!：型：!b：生，1 2一 乎((((”惫每)+o)咱)一 删(((”忌等)+0)确^)+号) =(^+鲁)((愚每)+0)一 等si叫掣一。][蝗掣一。]2一 栗苹，等： 三角调频连续波建模与数值仿真 鲁(((走每)+o)一((等)+o)+孥) =(如+夸)(志等)一等(正一-+·)=寺^t。 惫=2n+1，雄=0，±1，±2，… (14) 可见式(3)和式(4)满足式(2)的积分关系。因此式(3)和 式(4)所对应的频率表达式和相位表达式是三角调频连续波 的数肇表汶式． 4三角调频连续波的仿真 为了更形象地说明式(3)和式(4)之间的微分、积分关系， 图6三角调频的频率 图7三角调频的相位 和相位的微分 和频率的积分 将相位表达式进行微分再 除以27c所对应的曲线(三 角形标记)与频率曲线(实置 线)进行对比，如图6所旨 示，两者完全重合。频率、 进行积分后乘以2兀的曲 线(三角形标记)与相位曲 线(实线)进行对比，如图7 所示，完全重合。图6与 0 lO 20 30 40 50 ||s 图8具有指定参数的 三角调频的波形示例 图7中曲线所取的参数为 fo=1、厶=2、to=O、t。=20、90=0，采用相同的参数对 三角调频连续波的波形进行仿真，结果如图8所示。波形在 每个周期开始时频率较慢，在每前半个周期中逐渐加快，在每 个周期中间频率达到最快，在每后半个周期中逐渐减慢，在每 个周期结束时频率恢复到每周期开始的频率。 5结论 通过引入模数函数、绝对值函数和符号函数，给出了三角 调频连续波的频率和相位的数学表达式。数学表达式满足微 积分的关系，并且能够正确地描述跨越调频周期时的不连续 性。对模型进行了建模和仿真。该数学表达式为三角调频连 续波的理论研究提供了一定的参考。 参考文献： [1]沈兆欣．调频激光雷达空间测鼋技术探讨[J]．宇航计测技术， 2005．25(4)：5—10． [2]贾兴泉．连续波雷达数据处理[M]．北京：国防工业出版社， 2005． [3]William Ruff，Keith Aliberti，John Dammann，et a1．Performance of 柚FM／cw prototype ladar using a 32一eleraent linear self-mixing de— tector array[-J]．ProceedingsofSPIE，2003，5086：58---69 [4]Wolfram Research，Inc．Introduction tO the rounding and congru— ence functions[EB／OL]．http：／／functions．wolfram．eom／Inte— gerFunctions／Mod／introductions／FloorRelated／ShowAll．htrnl． [5]Wolfram Rdsearch．Introduction tO the complex components[EB／ oL]．http：／／functions．wolfram．com／Complex(kmagxments／Abs／ introductions／ComplexComplements／ShowAll．htrnl 183 ˝ • ‰ ˚