第1页 / 共10页
第2页 / 共10页
第3页 / 共10页
第4页 / 共10页
第5页 / 共10页
第6页 / 共10页
第7页 / 共10页
第8页 / 共10页
任意四边形上的积分.pdf
Numerical integrations over an arbitrary quadrilateral region
Introduction
Formulation of integrals over an arbitrary quadrilateral region
Algorithm and program
Numerical examples
Conclusions
References
Applied Mathematics and Computation 210 (2009) 515–524
Contents lists available at ScienceDirect
Applied Mathematics and Computation
j o u r n a l h o m e p a g e : w w w . e l s e v i e r . c o m / l o c a t e / a m c
Numerical integrations over an arbitrary quadrilateral region
Md. Shafiqul Islam *, M. Alamgir Hossain
Department of Mathematics, University of Dhaka, Dhaka 1000, Bangladesh
a r t i c l e
i n f o
a b s t r a c t
Keywords:
Double integral
Numerical integration
Quadrilateral and triangular finite element
Gaussian quadrature
In this paper, double integrals over an arbitrary quadrilateral are evaluated exploiting finite
element method. The physical region is transformed into a standard quadrilateral finite
element using the basis functions in local space. Then the standard quadrilateral is subdi-
vided into two triangles, and each triangle is further discretized into 4 n2 right isosceles
triangles, with area 1
2n2, and thus composite numerical integration is employed. In addition,
the affine transformation over each discretized triangle and the use of linearity property of
integrals are applied. Finally, each isosceles triangle is transformed into a 2-square finite
element to compute new n2 extended symmetric Gauss points and corresponding weight
coefficients, where n is the lower order conventional Gauss Legendre quadratures. These
new Gauss points and weights are used to compute the double integral. Examples are con-
sidered over an arbitrary domain, and rational and irrational integrals which can not be
evaluated analytically.
Ó 2009 Elsevier Inc. All rights reserved.
1. Introduction
Numerical simulation in engineering science and in applied mathematics has become a powerful tool to model the
physical phenomena, particularly when analytical solutions are not available and/or are very difficult to obtain. The integrals
arising in practical problems are not always simple or polynomial but rational and irrational expressions, in which the quad-
rature scheme cannot evaluate exactly [12]. Even there is no order of Gauss quadrature that will evaluate these integrals
exactly [9,10]. The integration points have to be increased in order to improve the integration accuracy and it is desirable
to make these evaluations by using as few Gauss points as possible, from the point of view of the computational efficiency.
Among various numerical techniques, the finite element method (FEM) is probably one of the most widely accepted even for
the complex geometries. This advantage is supported by the element wise coordinate transformation from one space to the
other space.
From the literature review we may realize that a lot of works of numerical integration using Gauss quadrature over tri-
angular region has been done [1–8,13], but a limited work is attempted over the quadrilateral region, such as [12]. Rathod
[11] presented some analytical formulas for rational integrals over quadrilateral element but it was confined with monomi-
als as numerators. For this, a little work has been done in this study to carry out the development of a good numerical inte-
gration technique over the arbitrary convex quadrilateral region with the advent of FEM.
Very recently, a rigorous and elaborate survey has been reported in the literature [13] by Rathod et al., and they have
derived various orders of extended numerical quadrature rules based on classical Gauss Legendre formula. In their work,
a transformation has been used from standard triangular surface to a standard 2-square. All the formulations are derived,
and all the examples are tested for certain triangular region. In contrast to this study, we use an arbitrary quadrilateral region
with convex and straight sides, which is transformed into a standard square finite element by coordinate transformations.
* Corresponding author.
E-mail address: mdshafiqul@yahoo.com (Md. Shafiqul Islam).
0096-3003/$ - see front matter Ó 2009 Elsevier Inc. All rights reserved.
doi:10.1016/j.amc.2009.01.030
516
Md. Shafiqul Islam, M. Alamgir Hossain / Applied Mathematics and Computation 210 (2009) 515–524
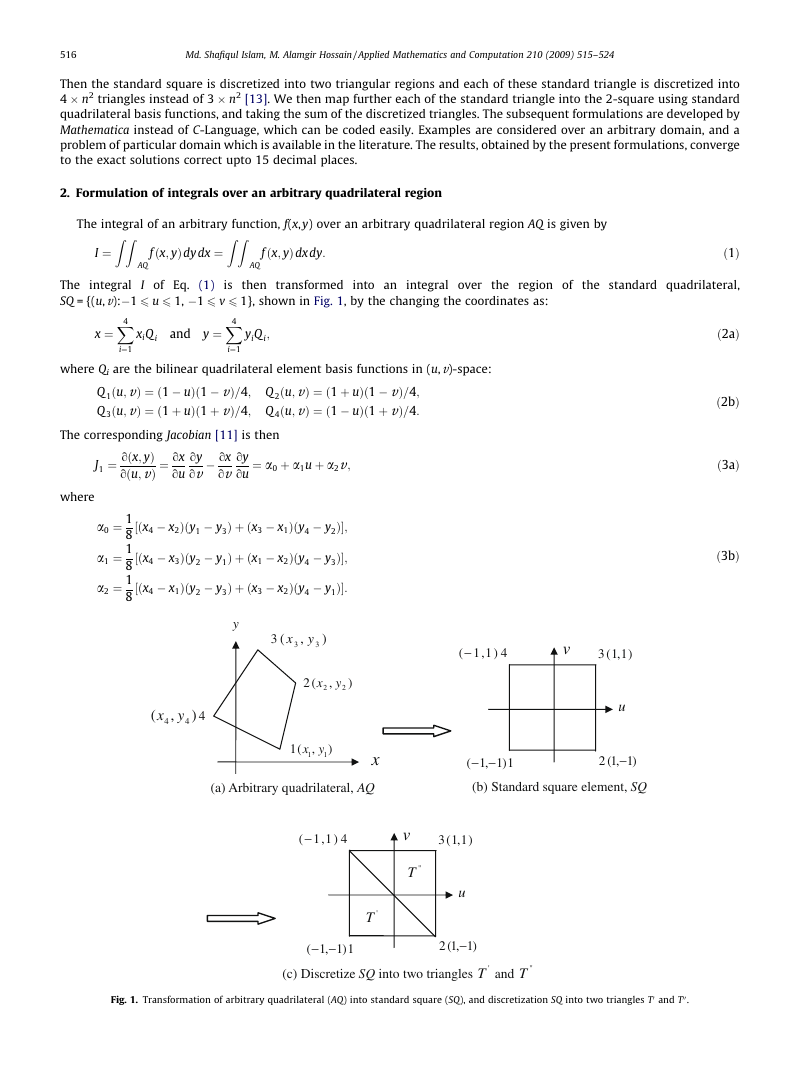
Then the standard square is discretized into two triangular regions and each of these standard triangle is discretized into
4 n2 triangles instead of 3 n2 [13]. We then map further each of the standard triangle into the 2-square using standard
quadrilateral basis functions, and taking the sum of the discretized triangles. The subsequent formulations are developed by
Mathematica instead of C-Language, which can be coded easily. Examples are considered over an arbitrary domain, and a
problem of particular domain which is available in the literature. The results, obtained by the present formulations, converge
to the exact solutions correct upto 15 decimal places.
2. Formulation of integrals over an arbitrary quadrilateral region
The integral of an arbitrary function, f(x, y) over an arbitrary quadrilateral region AQ is given by
I ¼
fðx; yÞdydx ¼
AQ
fðx; yÞ dxdy:
AQ
The integral
SQ = {(u,v): 1 6 u 6 1, 1 6 v 6 1}, shown in Fig. 1, by the changing the coordinates as:
is then transformed into an integral over the region of
I of Eq.
(1)
Z Z
X
4
i¼1
x ¼
xiQ i
and y ¼
Z Z
X
4
yiQ i;
i¼1
ð1Þ
the standard quadrilateral,
ð2aÞ
ð2bÞ
ð3aÞ
ð3bÞ
where Qi are the bilinear quadrilateral element basis functions in (u,v)-space:
Q 1ðu; vÞ ¼ ð1 uÞð1 vÞ=4; Q 2ðu; vÞ ¼ ð1 þ uÞð1 vÞ=4;
Q 3ðu; vÞ ¼ ð1 þ uÞð1 þ vÞ=4; Q 4ðu; vÞ ¼ ð1 uÞð1 þ vÞ=4:
The corresponding Jacobian [11] is then
J1 ¼
oðx; yÞ
oðu; vÞ ¼
ox
ou
oy
ov
ox
ov
oy
ou
¼ a0 þ a1u þ a2v;
where
a0 ¼ 1
8
a1 ¼ 1
8
a2 ¼ 1
8
½ðx4 x2Þðy1 y3Þ þ ðx3 x1Þðy4 y2Þ;
½ðx4 x3Þðy2 y1Þ þ ðx1 x2Þðy4 y3Þ;
½ðx4 x1Þðy2 y3Þ þ ðx3 x2Þðy4 y1Þ:
y
(3
x
,
3 y
3
)
(2
x
,
2 y
2
)
(
x
,
4 y
4
4)
4)1,1(−
v
)1,1(3
u
)1,1(2 −
(1
1 yx
1
,
)
x
−−
1)1,1(
(a) Arbitrary quadrilateral, AQ
(b) Standard square element, SQ
4)1,1(−
'T
−−
1)1,1(
v
''T
)1,1(3
u
)1,1(2 −
Fig. 1. Transformation of arbitrary quadrilateral (AQ) into standard square (SQ), and discretization SQ into two triangles T0 and T00.
(c) Discretize SQ into two triangles
'T and
''T
Md. Shafiqul Islam, M. Alamgir Hossain / Applied Mathematics and Computation 210 (2009) 515–524
517
3)1,1(−
v
''T
)1,1(1
u
−
)1,1(2
3)1,1(−
v
'T
−−
1)1,1(
u
−
)1,1(2
Fig. 2. Transformation of T00 into T0.
Z Z
Now use Eqs. (1)–(3) to obtain,
I ¼
fðx; yÞdy dx ¼
AQ
SQ
fðxðu; vÞ; yðu; vÞÞjJ1j dudv ¼
gðu; vÞ dudv ¼
SQ
where, g(u,v) = f(u,v)jJ1j.
Now discretize SQ into two triangles T0 and T00, shown in Fig. 1c, then
Z Z
I ¼
gðu; vÞdudv ¼
SQ
gðu; vÞ dudv þ
T0
gðu; vÞ dudv;
T00
Z Z
Z Z
Z Z
Z Z
Z
Z
1
1
1
1
gðu; vÞ dudv;
ð4Þ
ð5Þ
where T0 = {(u,v): 1 6 v 6 1, 1 6 u 6 v} and T00 = {(u,v): 1 6 u 6 1, u 6 v 6 1}.
T0 = {(u,v): 1 6 v 6 1, 1 6 u 6 v}, using simple coordinate transformation as shown in Fig. 2, such that:
The second integral of Eq. (5) is then transformed into an integral over the region of the same standard triangle,
Z Z
Z Z
T00
gðu; vÞdudv ¼
Z Z
Then Eq. (5) leads us
T0
gð v; uÞ dudv:
Z Z
I ¼
gðu; vÞdudv ¼
where,F(u,v) = g(u,v) + g( v, u).
SQ
½gðu; vÞ þ gð v; uÞdudv ¼
T0
standard quadrilateral basis functions, Qi(n,g), as shown in Fig. 3.
Z
Z
1
v
1
1
Fðu; vÞdudv;
ð6Þ
ð7Þ
The integral I of Eq. (7) can be further transformed into an integral over the standard 2-square, {(n,g): 1 6 n,g 6 1} using
ð8aÞ
ð8bÞ
ð8cÞ
Assume that
4
X
X
i¼1
4
i¼1
u ¼
v ¼
and
uiQ iðn; gÞ ¼ 1
4
v iQ iðn; gÞ ¼ 1
4
ð 1 þ 3n g ngÞ ¼ uðn; gÞ;
ð 1 n þ 3g ngÞ ¼ vðn; gÞ;
J2 ¼
ou
on
ov
og
ou
og
ov
on
¼ 1
4
ð2 n gÞ:
Notice that J1 depends on the vertices of the given arbitrary quadrilateral region, but J2 is fixed.
4)1,1( −
v
)0,0(3
u
−−
1)1,1(
−
)1,1(2
(a) Standard triangle, ST
4)1,1(−
η
)1,1(3
ξ
−
)1,1(2
−−
1)1,1(
(b) Standard square, SQ
Fig. 3. Transformation of standard triangle ST into 2-square SQ. (a) Standard triangle, ST. (b) Standard square, SQ.
518
Md. Shafiqul Islam, M. Alamgir Hossain / Applied Mathematics and Computation 210 (2009) 515–524
1)2,1( −
y
)4,1(4
)3,3(3
1R
)1,2(2
x
Then the Eq. (7) reduces to
1
1
1
1
Fðuðn; gÞ; vðn; gÞÞjJ2jdndg
1
1
4
4
ð 1 þ 3n g ngÞ;
F
Fig. 4. Quadrilateral region R1.
ð 1 n þ 3g ngÞ
1
4
ð2 n gÞdndg:
ð9Þ
Now Eq. (9) represents an integral over the standard 2-square region: {(n,g): 1 6 n,g 6 1}. Hence using conventional Gauss
Legendre quadrature rule for the integral I of Eq. (9), we have
ð2 gj niÞwiwj F
1
4
ð 1 þ 3ni gj nigjÞ;
1
4
1
4
ð 1 ni þ 3gj nigjÞ
;
Z
Z
Z
Z
1
1
1
1
I ¼
¼
X
s
X
s
i¼1
j¼1
I ¼
where (ni,gj) are Gaussian points in the (n,g) directions of order s, and wi, wj are the corresponding weight coefficients [4].
We can write Eq. (10) as:
ð 1 þ 3ni gj nigjÞ;
k ¼ 1
y0
4
ð 1 ni þ 3gj nigjÞ;
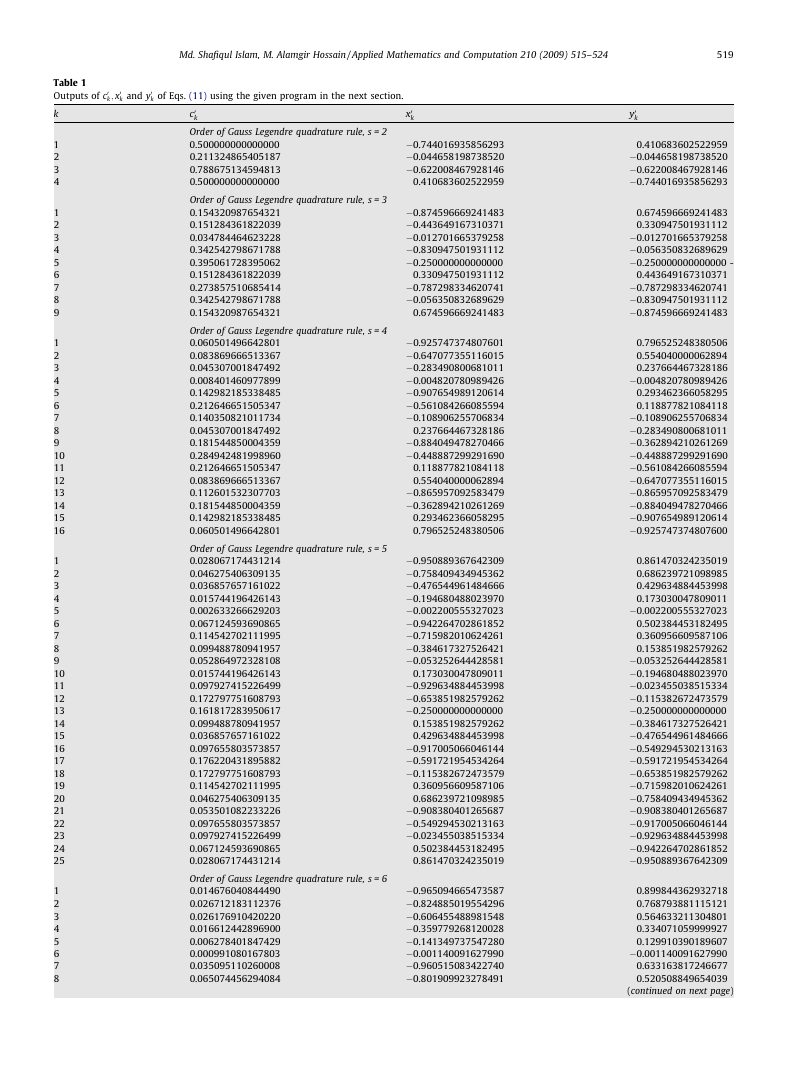
The weighting coefficients c0
kÞ of various order can be now easily computed from Eq. (11).
k and sampling points ðx0
k; y0
k and y0
k; x0
Using the given program in Mathematica, the outputs of c0
Now we discretize ST = {(u,v): 1 6 v 6 1, 1 6 u 6 v} in (u,v)-space of Eq. (7) into 4(n n) = 4n2 right isosceles triangle,
k for s = 2, 3, 4, 5, 6,7 are given in Table 1.
each Ti of area 1/(2n2) [13]. Then Eq. (7) reduces to
I ¼
Fðu; vÞ dudv:
ð12Þ
Since each Ti is to be transformed again into a standard triangle, and using composite integration rule [13] we can obtain the
following:
I ¼ 1
4n2
kHðx0
c0
X
ð13Þ
N¼ss
X
N¼ss
I ¼
kFðx0
c0
kÞ;
k; y0
k can be written in the form:
where c0
k¼1
k and y0
ð2 ni gjÞwiwj;
k; x0
k ¼ 1
c0
4
k ¼ 1
x0
4
where k = 1,2, . . ., N, and i, j = 1,2, . . ., s
Z Z
X
4ðnnÞ
i¼1
Ti
k¼1
kÞ;
k; y0
k þ 2ði nÞ þ 1
x0
x0
X
X
j¼0
2n 2 i
2n
k þ 2ði nÞ þ 1
F
;
2n 1 i
F
2n 1
X
X
i¼0
þ
2n 2
2n
i¼0
j¼0
k þ 2ðj nÞ þ 1
y0
2n
k þ 2ðj nÞ þ 1
y0
;
2n
;
Hðx0
k; y0
kÞ ¼
where
and
k ¼ 1
c0
4
k ¼ 1
y0
4
k ¼ 1
ð2 np gqÞwpwq;
ð 1 þ 3np gq npgqÞ;
x0
4
ð 1 np þ 3gq npgqÞ;
ðk ¼ 1; 2; . . .; N; p; q ¼ 1; 2; . . . ; sÞ:
ð10Þ
ð11aÞ
ð11bÞ
ð14aÞ
ð14bÞ
Md. Shafiqul Islam, M. Alamgir Hossain / Applied Mathematics and Computation 210 (2009) 515–524
519
Table 1
Outputs of c0
k of Eqs. (11) using the given program in the next section.
k; x0
k and y0
k
1
2
3
4
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
1
2
3
4
5
6
7
8
c0
k
Order of Gauss Legendre quadrature rule, s = 2
0.500000000000000
0.211324865405187
0.788675134594813
0.500000000000000
Order of Gauss Legendre quadrature rule, s = 3
0.154320987654321
0.151284361822039
0.034784464623228
0.342542798671788
0.395061728395062
0.151284361822039
0.273857510685414
0.342542798671788
0.154320987654321
Order of Gauss Legendre quadrature rule, s = 4
0.060501496642801
0.083869666513367
0.045307001847492
0.008401460977899
0.142982185338485
0.212646651505347
0.140350821011734
0.045307001847492
0.181544850004359
0.284942481998960
0.212646651505347
0.083869666513367
0.112601532307703
0.181544850004359
0.142982185338485
0.060501496642801
Order of Gauss Legendre quadrature rule, s = 5
0.028067174431214
0.046275406309135
0.036857657161022
0.015744196426143
0.002633266629203
0.067124593690865
0.114542702111995
0.099488780941957
0.052864972328108
0.015744196426143
0.097927415226499
0.172797751608793
0.161817283950617
0.099488780941957
0.036857657161022
0.097655803573857
0.176220431895882
0.172797751608793
0.114542702111995
0.046275406309135
0.053501082233226
0.097655803573857
0.097927415226499
0.067124593690865
0.028067174431214
Order of Gauss Legendre quadrature rule, s = 6
0.014676040844490
0.026712183112376
0.026176910420220
0.016612442896900
0.006278401847429
0.000991080167803
0.035095110260008
0.065074456294084
x0
k
0.744016935856293
0.044658198738520
0.622008467928146
0.410683602522959
0.874596669241483
0.443649167310371
0.012701665379258
0.830947501931112
0.250000000000000
0.330947501931112
0.787298334620741
0.056350832689629
0.674596669241483
0.925747374807601
0.647077355116015
0.283490800681011
0.004820780989426
0.907654989120614
0.561084266085594
0.108906255706834
0.237664467328186
0.884049478270466
0.448887299291690
0.118877821084118
0.554040000062894
0.865957092583479
0.362894210261269
0.293462366058295
0.796525248380506
0.950889367642309
0.758409434945362
0.476544961484666
0.194680488023970
0.002200555327023
0.942264702861852
0.715982010624261
0.384617327526421
0.053252644428581
0.173030047809011
0.929634884453998
0.653851982579262
0.250000000000000
0.153851982579262
0.429634884453998
0.917005066046144
0.591721954534264
0.115382672473579
0.360956609587106
0.686239721098985
0.908380401265687
0.549294530213163
0.023455038515334
0.502384453182495
0.861470324235019
0.965094665473587
0.824885019554296
0.606455488981548
0.359779268120028
0.141349737547280
0.001140091627990
0.960515083422740
0.801909923278491
y0
k
0.410683602522959
0.044658198738520
0.622008467928146
0.744016935856293
0.674596669241483
0.330947501931112
0.012701665379258
0.056350832689629
0.250000000000000 -
0.443649167310371
0.787298334620741
0.830947501931112
0.874596669241483
0.796525248380506
0.554040000062894
0.237664467328186
0.004820780989426
0.293462366058295
0.118877821084118
0.108906255706834
0.283490800681011
0.362894210261269
0.448887299291690
0.561084266085594
0.647077355116015
0.865957092583479
0.884049478270466
0.907654989120614
0.925747374807600
0.861470324235019
0.686239721098985
0.429634884453998
0.173030047809011
0.002200555327023
0.502384453182495
0.360956609587106
0.153851982579262
0.053252644428581
0.194680488023970
0.023455038515334
0.115382672473579
0.250000000000000
0.384617327526421
0.476544961484666
0.549294530213163
0.591721954534264
0.653851982579262
0.715982010624261
0.758409434945362
0.908380401265687
0.917005066046144
0.929634884453998
0.942264702861852
0.950889367642309
0.899844362932718
0.768793881115121
0.564633211304801
0.334071059999927
0.129910390189607
0.001140091627990
0.633163817246677
0.520508849654039
(continued on next page)
520
Md. Shafiqul Islam, M. Alamgir Hossain / Applied Mathematics and Computation 210 (2009) 515–524
Table 1 (continued)
k
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
c0
k
0.066568810067974
0.046428710417516
0.022046614973247
0.006278401847429
0.053988206897587
0.102236557019614
0.109471725083648
0.083349671145065
0.046428710417516
0.016612442896900
0.063552674420906
0.122376656670072
0.135593779022232
0.109471725083648
0.066568810067974
0.026176910420220
0.055528891524955
0.108102297614921
0.122376656670072
0.102236557019614
0.065074456294084
0.026712183112376
0.028361001521177
0.055528891524955
0.063552674420906
0.053988206897587
0.035095110260008
0.014676040844490
Order of Gauss Legendre quadrature rule, s = 7
0.008383178231877
0.016229336623041
0.018005727931648
0.014218420393005
0.007972981898571
0.002801080689151
0.000426637441423
0.019988306531199
0.039117553014085
0.044437151163993
0.036780461704774
0.022765035551479
0.010110667549803
0.002801080689151
0.031435523240266
0.062362772594912
0.072897093734371
0.063602544468903
0.043312161692773
0.022765035551479
0.007972981898571
0.039901010364923
0.080124975391153
0.095986831742216
0.087344939608496
0.063602544468903
0.036780461704774
0.014218420393005
0.041468269273342
0.084034888207426
0.102482025775969
0.095986831742216
0.072897093734371
0.044437151163993
0.018005727931648
0.033416562465088
0.068124438478366
0.084034888207426
0.080124975391153
0.062362772594912
0.039117553014085
0.016229336623041
x0
k
0.554822424771676
0.275782268461456
0.028694769954641
0.129910390189607
0.953380653041526
0.766117524963210
0.474384407091445
0.144925185950153
0.146807931921612
0.334071059999927
0.945323618263202
0.725696554736187
0.383544372033350
0.002853965074949
0.345006147777786
0.564633211304801
0.938189187881988
0.689904156420906
0.303106354353119
0.133711047586252
0.520508849654039
0.768793881115121
0.933609605831142
0.666929060145101
0.251473290143247
0.217708047244823
0.633163817246677
0.899844362932718
0.973906455024851
0.867477088409913
0.695363130529180
0.487276978085690
0.279190825642200
0.107076867761467
0.000647501146528
0.971265451781595
0.854064060795283
0.664529950865235
0.435382796399849
0.206235641934462
0.016701532004414
0.100499858981898
0.966994511011860
0.832372967976233
0.614667579653261
0.351461287844349
0.088254996035437
0.129450392287535
0.264071935323162
0.961830934257069
0.806148389199546
0.554383863533048
0.250000000000000
0.054383863533048
0.306148389199546
0.461830934257069
0.956667357502278
0.779923810422858
0.494100147412834
0.148538712155651
0.197022723101533
0.482846386111557
0.659589933190977
0.952396416732544
0.758232717603808 -
0.444237776200861
0.064617203600152
0.315003369000558
0.628998310403505
0.823162009532241
y0
k
0.345006147777786
0.146807931921612
0.028694769954641
0.141349737547280
0.217708047244823
0.133711047586252
0.002853965074949
0.144925185950153
0.275782268461456
0.359779268120028
0.251473290143247
0.303106354353119
0.383544372033350
0.474384407091445
0.554822424771676
0.606455488981548
0.666929060145101
0.689904156420906
0.725696554736187
0.766117524963210
0.801909923278491
0.824885019554296
0.933609605831142
0.938189187881988
0.945323618263202
0.953380653041526
0.960515083422740
0.965094665473587
0.924309369660667
0.823162009532241
0.659589933190977
0.461830934257069
0.264071935323162
0.100499858981898
0.000647501146528
0.719373646160558
0.628998310403505
0.482846386111557
0.306148389199546
0.129450392287535
0.016701532004414
0.107076867761467
0.387958552708296
0.315003369000558
0.197022723101533
0.054383863533048
0.088254996035437
0.206235641934462
0.279190825642200
0.012723021914310
0.064617203600152
0.148538712155651
0.250000000000000
0.351461287844349 -
0.435382796399849
0.487276978085690
0.413404596536916
0.444237776200861
0.494100147412834
0.554383863533048
0.614667579653261
0.664529950865235
0.695363130529179
0.744819689989179
0.758232717603808 -
0.779923810422858
0.806148389199546
0.832372967976233
0.854064060795283
0.867477088409913
Md. Shafiqul Islam, M. Alamgir Hossain / Applied Mathematics and Computation 210 (2009) 515–524
521
Table 1 (continued)
k
43
44
45
46
47
48
49
c0
k
0.016339719022330
0.033416562465088
0.041468269273342
0.039901010364923
0.031435523240266
0.019988306531199
0.008383178231877
3. Algorithm and program
x0
k
0.949755413489287
0.744819689989179
0.413404596536916
0.012723021914310
0.387958552708296
0.719373646160558
0.924309369660667
y0
k
0.949755413489287
0.952396416732544
0.956667357502278
0.961830934257069
0.966994511011860
0.971265451781595
0.973906455024851
Now we give an algorithm and the corresponding Mathematica program of the formulation of the above results in the
following:
Algorithm.
Step 1: Input (conventional) Gauss Legendre quadrature rule of order s.
Step 2: Set up a subalgorithm for generating new weighting coefficients c0
k and sampling points ðx0
k; y0
kÞ to be called STrian-
gle(s) that accepts as input the order of Gauss Legendre quadrature rule s s, and defined by the following:
For i = 1,2,3,. . . , s
For j = 1,2,3,. . . , s
Set k = i + (s j)s
Set the Eq. (11b)
Step 3: Call subprogram STriangle(s).
Step 4: Input the value of n then T will be discretized into 4 n2 subtriangles Ti.
Step 5: Set F(u,v) = f(u,v) + f( v, u).
Step 6: For m = 1,2,3,. . . , n do steps 7 and 8.
Step 7: For k = 1,2,3,. . . , s2
Set the Eqs. (14)
Step 8: Set the Eq. (13)
Step 9: Output for m = 1,2,3,. . . , n, the results of the required double integral using 4 m2 subtriangles.
Mathematica program
< NumericalMath ‘GaussianQuadrature’
STriangle[s0_]:¼Module[{s=s0},
C1 = Table[0,{i, 1, s2}]; X1 = Table[0,{i, 1, s2}]; Y1 = Table[{0, i, 1, s2}];
XI = Table[0,{i, 1, s}]; WI = Table[0,{i, 1, s}];
GQ = GaussianQuadratureWeights [s, 1, 1];
Do [{XIsit = GQsi, 1t;
For [i = 1, i 6 s, i++, For[j = 1, j 6 s, j++, k = i + (s j) s;
WIsit = GQsi, 2t;}, {i, 1, s}];
C1 skt ¼ 2 XI sit XI sjt
WI sitWI sjt;
X1 skt ¼ 1þ3XI sit XI sjt XI sitXI sjt
;
Y1 skt ¼ 1 XI sitþ3XI sjt XI sitXI sjt
;;;;
4
4
4
s = Input[‘‘Enter the Order of Gauss Legendre Quadrature rule:”];
STriangle[s];
TableForm[Table[{PaddedForm[C1sit,{20, 15}], PaddedForm[X1sit//N,{20, 15}],
PaddedForm[Y1sit//N, {20, 15}]}, {i, 1, s2}],
TableHeadings -> {None,{”ntntnt” ‘‘Ck”,”ntntnt” ‘‘Xk”, ”ntntnt” ‘‘Yk”}}]
(*This generates new weighting coefficients and sampling points*)
208
104
s = Input[”Enter the Order of Gauss Legendre Quadrature rule:”];
STriangle[s]
; c2 ¼ 328125
c1 ¼ 65625
f½x ; y :¼ c1x8þc2y9þc3x7y6
d1x9þd2y7þd3
F[x_, y_]:¼f[x, y]+f [-y, -x]
H1 = Table[0, {i, 1, 4 s2}];
n = Input[‘‘Enter the value of n then discretise T into 4 n2 triangle:”];
App = Table [0, {i, 1, n}];
; c3 ¼ 239062
; (*Example 2 *)
; d1 ¼ 1; d2 ¼ 125
; d3 ¼ 175
4 ;
208
4
522
Md. Shafiqul Islam, M. Alamgir Hossain / Applied Mathematics and Computation 210 (2009) 515–524
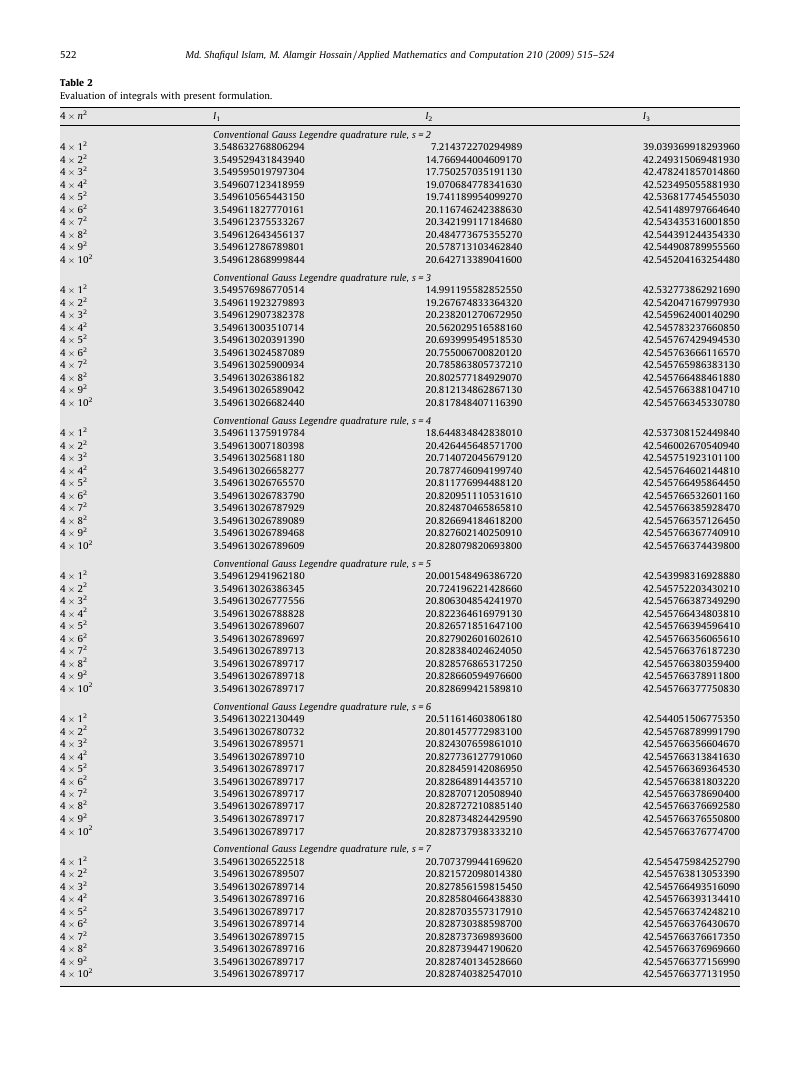
Table 2
Evaluation of integrals with present formulation.
4 n2
I1
I2
I3
4 12
4 22
4 32
4 42
4 52
4 62
4 72
4 82
4 92
4 102
4 12
4 22
4 32
4 42
4 52
4 62
4 72
4 82
4 92
4 102
4 12
4 22
4 32
4 42
4 52
4 62
4 72
4 82
4 92
4 102
4 12
4 22
4 32
4 42
4 52
4 62
4 72
4 82
4 92
4 102
4 12
4 22
4 32
4 42
4 52
4 62
4 72
4 82
4 92
4 102
4 12
4 22
4 32
4 42
4 52
4 62
4 72
4 82
4 92
4 102
Conventional Gauss Legendre quadrature rule, s = 2
3.548632768806294
3.549529431843940
3.549595019797304
3.549607123418959
3.549610565443150
3.549611827770161
3.549612375533267
3.549612643456137
3.549612786789801
3.549612868999844
7.214372270294989
14.766944004609170
17.750257035191130
19.070684778341630
19.741189954099270
20.116746242388630
20.342199117184680
20.484773675355270
20.578713103462840
20.642713389041600
Conventional Gauss Legendre quadrature rule, s = 3
3.549576986770514
3.549611923279893
3.549612907382378
3.549613003510714
3.549613020391390
3.549613024587089
3.549613025900934
3.549613026386182
3.549613026589042
3.549613026682440
14.991195582852550
19.267674833364320
20.238201270672950
20.562029516588160
20.693999549518530
20.755006700820120
20.785863805737210
20.802577184929070
20.812134862867130
20.817848407116390
Conventional Gauss Legendre quadrature rule, s = 4
3.549611375919784
3.549613007180398
3.549613025681180
3.549613026658277
3.549613026765570
3.549613026783790
3.549613026787929
3.549613026789089
3.549613026789468
3.549613026789609
18.644834842838010
20.426445648571700
20.714072045679120
20.787746094199740
20.811776994488120
20.820951110531610
20.824870465865810
20.826694184618200
20.827602140250910
20.828079820693800
Conventional Gauss Legendre quadrature rule, s = 5
3.549612941962180
3.549613026386345
3.549613026777556
3.549613026788828
3.549613026789607
3.549613026789697
3.549613026789713
3.549613026789717
3.549613026789718
3.549613026789717
20.001548496386720
20.724196221428660
20.806304854241970
20.822364616979130
20.826571851647100
20.827902601602610
20.828384024624050
20.828576865317250
20.828660594976600
20.828699421589810
Conventional Gauss Legendre quadrature rule, s = 6
3.549613022130449
3.549613026780732
3.549613026789571
3.549613026789710
3.549613026789717
3.549613026789717
3.549613026789717
3.549613026789717
3.549613026789717
3.549613026789717
20.511614603806180
20.801457772983100
20.824307659861010
20.827736127791060
20.828459142086950
20.828648914435710
20.828707120508940
20.828727210885140
20.828734824429590
20.828737938333210
Conventional Gauss Legendre quadrature rule, s = 7
3.549613026522518
3.549613026789507
3.549613026789714
3.549613026789716
3.549613026789717
3.549613026789714
3.549613026789715
3.549613026789716
3.549613026789717
3.549613026789717
20.707379944169620
20.821572098014380
20.827856159815450
20.828580466438830
20.828703557317910
20.828730388598700
20.828737369893600
20.828739447190620
20.828740134528660
20.828740382547010
39.039369918293960
42.249315069481930
42.478241857014860
42.523495055881930
42.536817745455030
42.541489797664640
42.543435316001850
42.544391244354330
42.544908789955560
42.545204163254480
42.532773862921690
42.542047167997930
42.545962400140290
42.545783237660850
42.545767429494530
42.545763666116570
42.545765986383130
42.545766488461880
42.545766388104710
42.545766345330780
42.537308152449840
42.546002670540940
42.545751923101100
42.545764602144810
42.545766495864450
42.545766532601160
42.545766385928470
42.545766357126450
42.545766367740910
42.545766374439800
42.543998316928880
42.545752203430210
42.545766387349290
42.545766434803810
42.545766394596410
42.545766356065610
42.545766376187230
42.545766380359400
42.545766378911800
42.545766377750830
42.544051506775350
42.545768789991790
42.545766356604670
42.545766313841630
42.545766369364530
42.545766381803220
42.545766378690400
42.545766376692580
42.545766376550800
42.545766376774700
42.545475984252790
42.545763813053390
42.545766493516090
42.545766393134410
42.545766374248210
42.545766376430670
42.545766376617350
42.545766376969660
42.545766377156990
42.545766377131950
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
