DO I :10.13873/j .1000 -97872010.10.039 　　　　　　　　传 感器与微系统(TransducerandMicrosystemTechnologies)　　　　　　　　　 2010年 第 29卷 第 10期 116 计算与测试 基于牛顿 —拉夫逊迭代法的 6自由度机器人逆解算法 ＊ 王 　宪 , 杨国梁, 张方生, 丁　锋 (江南大学 通信与控制工程学院, 江苏 无锡 214122) 摘　要:为解决一般 6自由度旋转关节机器人逆 运动学问题, 提出了一种用牛顿 —拉夫逊迭代 法逐次逼近 目标位姿的逆解算法 。根据正 运动学方程建立雅克比矩阵, 采用基于豪斯霍 尔德的 SVD分解 求其伪逆来 避免雅克比矩阵的奇 异性问题, 通过建立迭代规则并逐次迭代找到最优的 逆运动学单解, 实际应用时无需 再建立多解 取优策略。 本算法具有较好的局部快速收敛性, 能够达到较好 的精度和速 度, 并 在基于 ARM9 的嵌入式系 统上实现了此算法。 相应的测试表明:算法实时性能够满足系 统要求, 可应用于机器人实时控 制系统。 关键词:机器人;运动控制;微分运动;6自由度旋转关节 中图分类号 :TP242　　　文献标识码:B　　　文章编号:1000 — 9787(2010)10— 0116 — 03 Aninversekinematicsalgorithm ofthegeneral6-DOF robotbasedonNewton-Raphsoniteration＊ WANGXian, YANGGuo-liang, ZHANGFang-sheng, DINGFeng (CollegeofCommunicationandControlEngineering, JiangnanUniversity, Wuxi214122, China) Abstract:Toresolvetheinversekinematicsproblemofthegeneral6-DOFrotaryjointrobot, aninversealgorithm isproposed, usingpseudo-inverseofJacobianmatrixtosolvedifferentialmovementandusingNewton-Raphson iterationtoapproximatetargetposition.Jacobianmatrixisestablishedaccordingtoforwardkinematics, usingSVD decompositionofHouseholdertoavoidthesingularityproblem.Thisalgorithmhasgoodandfastlocalconvergence, andcanachievehigherprecisionandtheidealspeed.ThealgorithmisrealizedonanARM9-basedembedded system.Thecorrespondingtestsshowthatthealgorithmisreal-timewhichcanmeetsystemrequirements.Itcanbe appliedtoreal-timerobotcontrolsystem;6 degreeoffreedom(DOF)rotaryjoinot Keywords:robot;motioncontrol;differentialmotion;6 degreeoffreedom(DOF)rotaryjoint 0　引　言 随着工业自动化 程度的不 断提高, 机 器人特 别是 6自 由度旋转关节机器人 以其较少的冗余和较大的自由度得到 了广泛的应用。 现代 工业机 器人多 采用在线 编程 的方式, 要求在满足必需的 精度的 前提下达 到较快 的速度, 这就 使 得作为机器 人控 制基 础的 运动 学问 题受 到越 来越 多的 重 视。 运动学分为正运 动学和 逆运动 学, 前 者一般 采用齐 次 坐标变换法 [ 1] , 此 种算 法简 单可 靠, 比 较成 熟。 后 者由 于 机器人本体的多变性 , 至 今没有 成熟的 算法 [ 2] 。 国内 的研 究一般集中 在 Puma560 或类 Puma560 等符 合 Pieper准 则 的机器人上, 如程 永伦 等人 [ 3, 4] 利用 旋转 子矩 阵正 交的 特 性, 通过矢量运 算构 造方 程等 方法 提高 了求 逆 解的 速度。 由于机器人的生产、装配 及使用 磨损等 不可避 免的会带 来 收稿日期 :2010— 04— 12 ＊基金项目 :国家自然科学基金资助项目 (60574051) 误差, 甚 至一些机器人在 设计时 就不 符合 Pieper准则。 针 对此时求解困难的问题, LeeHY等人 [ 5, 6] 通过 矢量乘法 运 算找到 14个线性无关的逆运动学方 程, 利用分离变量消 元 法将逆运动学问题简 化为关 节变量半 角正切 的一 元 16 次 方程求根问题, 但 此算法得到的运动学解不唯一, 需要进 一 步验证各解正确性并建立取优策略, 增加了算法运算量;金 媛媛等人 [ 7] 将局部 搜索 能力 强的 模拟 退 火算 法与 全局 搜 索能力强的遗传算法 相结合 提出了一 种逆运 动学解 法, 虽 然能达到一定的精度, 但程 序需要 占用较 大的存 储空间 且 存在迭代次数多、运算量较大的问题, 在嵌入式系统上难 以 达到较高的 实时 性。 本文 以雅 克比 矩阵 和 微分 运动 为 基 础, 提出 了一种用牛顿 —拉夫逊迭代法来求逆运动学解的 方 法, 采 用基 于 豪斯 霍 尔 德 的SVD分 解 求 雅 克比 矩 阵 的 伪 

第 10期　　　　　　　　　　王　宪, 等:基于牛顿 —拉夫逊迭代法的 6自由度机器人逆解算法　　　　　　　　　　　 117 逆来解决奇异性问题, 通过迭代可以得到 逆运动学 唯一解, 此解等同于按能量最小原则确 定的最终解。 算 法参数和所 需存储 空间均较少, 借助牛顿 —拉夫逊迭 代法的局部快速收 敛性, 以较少的迭代次数即可得到所需精度的解。 1　正运动学 正运动学是解决 如何将机器人的关节坐标 系转换到笛 卡尔坐标系的问 题。 本 文采用 齐次 坐标变 换法, 建 立机器 人 DenavitHarten-berg(DH)坐标系, 如图 1, 其中, X0Y0Z0 基坐标系, 其余为关节坐标系, a表示关节间杆件长 度。 为 图 1　DH坐标系 Fig 1　DHcoordinatesystem 　　根据 DH法则与定义的 4个连杆参数[ θαad] , 可得 从坐标系 Xn-1 Yn-1Zn-1到坐标系 XnYnZn的变换关系为 　 n-1 Tn=An=Rot(z, θn)×Trans(0, 0, dn)× 　Trans(an, 0, 0)×Rot(x, αn) = cosθn -sinθncosαn sinθnsinαn ancosθn sinθn cosθncosαn -cosθnsinαn ansinθn 0 0 sinαn 0 cosαn 0 dn 1 . (1) 从基座开始到末 端执行器的总齐次变 换公式 即为 T= A0 A1 A2A3 A4A5。 2　逆运动学 逆运动学是解决 在已知机器人位姿的条件 下如何求解 各关节角度 的问题。 牛 顿 —拉夫 逊迭 代法有 收敛 速度 快和 自我校正的优点 [ 8] , 上次迭 代产生 的误 差不会 传递 到下次 迭代中, 它是解非线 性方 程组的 一个 重要 方法。 为 了解决 迭代法中雅克比矩 阵奇 异或病 态时 无法进 行迭 代的 问题, 本文用伪逆代替雅克 比矩阵的伪逆 [ 8, 9] , 使得算法的应用范 围更加广泛。 合式(2)可得 v ω =J(θ)dθ dt=lim Δt※0 1 ΔtD , 即 Jdθ=D . (3) 雅克比矩阵 J中的每 个元素可由对应的运 动学方程 对 其中一个关节 变量 θi的 导数求 得。 对 式(3)两 边左 乘 J+ 得 dθ=J+D . (4) 由于 J可能 是一 个非 满秩 的方 阵, 所 以, 此 处 J+为 J 的伪逆。 由 如 下方 法 计 算, 对 J进 行 基 于 豪 斯 霍 尔 德 的 SVD分解得到 J=U∑ V＊(U为上三角矩阵, ∑ 是一个对 角 矩阵), 变形后可得 J+ =V∑ +U＊(∑ +是将∑ 转置, 并将 其 主对角线上每个非零元素 求倒数得到的, U＊为 U的共轭 转 置)。 此时关节角增量 dθ=V∑ +U＊ D . 式(5)即为建 立的牛顿 —拉夫逊迭代法的修正方程。 下面进行微 分运动向量 D的求解。 用微分算子乘以一 (5) 个坐标系将导致 坐标系的变化, 微分算子可由式(6)求得 Δ =Trans(dx, dy, dz)×Rot(k, dθ)-I 1 0 0 1 0 0 = 0 dx 0 dy 1 dz 0 0 0 1 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 = 　 0 　 1 -δz 　δy 0 　δz 　1 -δx 0 -δy 　δx 　1 　 0 　0 　0 　 0 -δz 　δy dx 　δz 　 0 -δz dy -δy 　δx 　 0 dz 　 0 　 0 　 0 1 0 - . (6) 微分运动可 以表示为由当 前位姿 Tcur运动到 目标位 姿 Tend Tend=Tcur(I+Δ), 即 Δ=Tcur (7) -1 Tend-I. 结合式(6)、式(7)可求 得 dx, dy, dz及 δx, δy, δz的值, 即得到微分运动 向量 D。 综上所述, 采用牛顿 —拉夫逊迭代 法求一般 6 自由度 旋 牛顿 —拉夫逊迭代法 需要用到微分运动 和雅克比 矩阵。 转关节机器人逆 运动学解的步骤为: 定义 6自由度旋转关节机器人关节坐 标系的广 义速度为线 速度 v和角速度 ω组成 的 6维 列向 量, 微分运 动则 描述为 微 分平移 d和微分旋转 δ组成的 6维列向量 D, 可由广义速 度对时间的导数求得 , 即有 v ω =lim Δt※0 1 Δt d δ =lim Δt※0 1 ΔtD . (2) 6自由度旋转关节机器 人笛卡 尔空间 的广义速 度和关 节空间的关节速度可 通过 6 ×6雅克比矩 阵 J相互 转换, 结 1)根据当前机 器人 的关节 角度 运用 正运 动学 求得 当 前位姿 Tcur(或直接用上次计算保留的当前位姿)。 2)以机器人末端坐标系作 为微分运动 的参考坐 标系, 设目标位姿为 Tend, 根据 当前 位姿计 算微 分运 动矩 阵:Δ= curTend-I, 根据式(6)的相应元素得到微分运动向量 D。 T-1 3)将正运动学方程各式分 别对各关节 角求导, 得到 雅 克比矩阵 J, 进 一步 建 立 牛 顿 —拉夫 逊 迭 代 法的 迭 代 方 程 Jdθ=D。 

　　　　　　　　　　　　　　　　　　　传 感 器 与 微 系 统　　　　　　　　　　　　　　　　　　　　第 29卷 118 4)对 J进行 SVD分 解并 变 形 求得 J的 伪 逆 J+, 由 dθ=J+(θ)D计算得到 dθ。 5)计算‖ dθ‖ , 设定一个 满足精度的 充分小的 数 eps, 当‖ dθ‖ ≤eps时, 退 出循环 并输 出当 前位姿 Tcur;当 循环 次数大于 N时, 循环 结束并 输出 失败信 息, 其中, N为满足 预定 循环 次 数 要求 的 自定 义 充分 大 的 整数;当 ‖ dθ‖ > eps, 且循环次数小于 N时, 令 θcur=θcur+dθ, 并计算 Tcur, 重 复步骤(1)至(5), 直至满足循 环退出条件, 此时 θcur即为满 足条件的机器人各关 节角度。 由于采用的是逐渐逼近目 标位姿的求解 策略, 所以, 不 存在多解问题, 迭代时 会趋近 于距 离当 前关节 角最 接近的 角度。 3　验　证 本文 所使用 的硬件 为一台 6自由度 焊接机 器人, 具有 6个旋转关节, 采 用基于 S3C2440(主 频 400MHz)的 嵌入式 系统通工业 以 太网 控制 驱 动器 驱 动 6 台 电机, 采用 Linux (版本 2.6.15)开源操作系统作为软 件平台, 应用程 序使用 面向对象的 C++语言编写, 系统结构如图 2。 图 2　系统结构框图 Fig2　System structurediagram 　　设定最大循环次 数为 N=100, 精度 eps=10 -6, 初始位 姿 Tcur= 1 0 0 0 0 1 0 0 0 0 1 0 。 0 0 0 1 3.1　算法正确性测试 对图 3所示 三角形 的三条 边进行焊 接实验, 设 各顶点 别为 A(-0.985 023, -19.378 845, 32.918 547), B(23.452 674, 8.329 251, 14.181 958), C(-2.186 015, -24.791 642, 14.181 958)。 为 了使 机 器人 末端 执 行器 沿三 条 边精 确运 动, 每条边 各取 70个等 分点, 分别 用本文逆 运动学 算法计 算对应的关节角度。 试 验时 机器人 从 A点 开始 焊接, 并沿 三条边依次经 B点、C点 后 再返 回到 A点, 此 过 程机 器人 6个关节的 角度变化情 况如图 4 所示。 将得到 的关节角度 代入正运动学中得 到末 端执行 器的 坐标, 此坐 标和 三角形 三条边上各等分点 相吻 合, 表 明算 法能 够正确 计算 逆运动 学解, 并达到所需要的精度。 3.2　算法迭代次数 迭 代次数 是衡量算 法收敛 性能好 坏的重 要指标, 根据 不同的精度, 取 1000次计算分别记录 逆运动学算 法迭代次 数, 结果取平均值, 如表 1。 在操作 机器人 时可以由 精度和 迭代次数的关系, 根据实际需要设置。 图 3　需要焊接的三角形图 Fig 3　Diagram oftriangleneededtoweld 图 4　各关节角的变化图 Fig4　Diagram ofvariousjointanglechanges 表 1　不同精度下的迭代次数 Tab 1　Numberofiterationsunderdifferentprecision 精度(rad) 10 -3 10 -6 10-9 迭代次数 23 47 60 3.3　算法性能测试 算法所用时间的长短 直接影响到机器人实 际控制时 的 实时性, 本次测试在基于嵌入式系统的 焊接机器人 上进行, 逆运动学结果精确到小数 点后 6位, 取 1 000次 计算并记 录 算法所用时间, 结果取平均值, 如表 2所示。 表 2　算法所用时间 Tab 2　Timeofalgorithm spent 正运动学 逆运动学 SVD分解 69.425 92.572 算法 时间(ms) 9.805 　　对雅克比 矩阵 进行 SVD分解 所用 的 时间 占到 了逆 运 动学算法总时间 的 75%, 可见 雅克比矩阵 分解算 法对整 个 逆运动学 解 法的 执行 时 间有 较大 影 响。 本文 采 用的 SVD 分解法虽然增加了 算法 的执行 时间, 但 很好 的解决 了雅 克 比矩阵奇异性 问题, 使得 算法 应用范 围更 广。 在本 嵌入 式 系统平台上, 对文献[ 3] 所提 算法进行 试验, 结果 虽然比 文 中算法所用时间 略短, 但 文献[ 3] 的算 法所得 为多解, 需 要 进一步确定最 优解, 再次 增加 了算法 时间 和复杂 性。 考 虑 到在此嵌入 式系 统平 台 上控 制机 器 人的 伺 服周 期为 微 秒 级, 文中所提算法完全能 够达到 所需要 求, 且 比文献 [ 3] 算 法更具优势。 4　结　论 本文在嵌入式系统上实现了一种一般 6自由度旋转关节 (下转第 131页) 

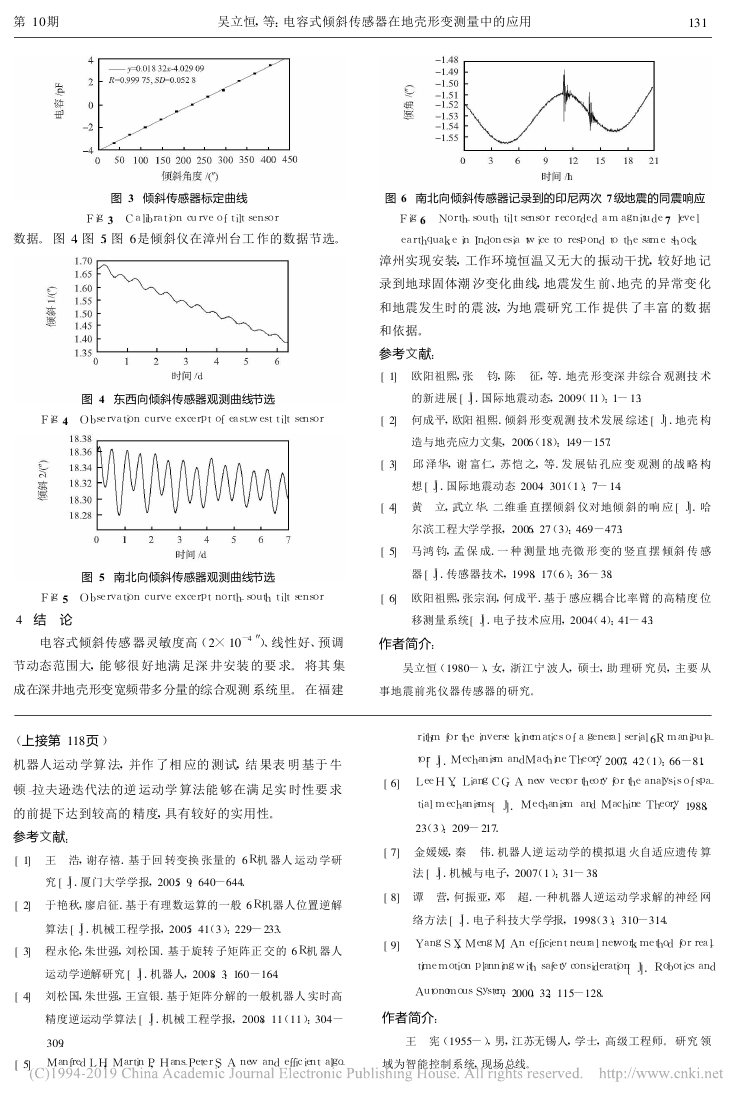
第 10期　　　　　　　　　　　　吴立恒, 等:电容式倾斜传感器在地壳形变测量中的应用　　　　　　　　　　　　　 131 图 3　倾斜传感器标定曲线 Fig 3　Calibrationcurveoftiltsensor 数据。 图 4, 图 5, 图 6是倾斜仪在漳州台工 作的数据节选。 图 6　南北向倾斜传感器记录到的印尼两次 7 级地震的同震响应 Fig6　North-southtiltsensorrecordedamagnitude7 level earthquakeinIndonesiatwicetorespondtothesameshock 漳州实现安装, 工作环境恒温又无大的 振动干扰, 较好地 记 录到地球固体潮 汐变化曲线, 地震发生 前、地壳 的异常变 化 和地震发生时的震 波, 为地 震研究 工作 提供 了丰富 的数 据 和依据。 参考文献 : [ 1] 　欧阳祖熙 , 张 　钧 , 陈 　征 , 等 .地壳 形变深 井综合 观测技 术 图 4　东西向倾斜传感器观测曲线节选 的新进展 [ J] .国际地震动态 , 2009(11):1-13. Fig 4　Observationcurveexcerptofeast-westtiltsensor [ 2] 　何成平 , 欧阳 祖熙 .倾斜 形变观测 技术发展 综述 [ J] .地壳 构 造与地壳应力文集 , 2006(18):149 -157. [ 3] 　邱 泽华 , 谢 富仁 , 苏恺 之 , 等 .发 展钻 孔应 变 观测 的战 略 构 想 [ J] .国际地震动态 2004, 301(1):7-14. [ 4] 　黄 　立 , 武立 华.二维垂 直摆倾斜 仪对地倾 斜的响 应 [ J] .哈 尔滨工程大学学报 , 2006, 27(3):469 -473. [ 5] 　马鸿 钧 , 孟 保 成 .一 种 测量 地 壳微 形 变的 竖直 摆 倾斜 传 感 图 5　南北向倾斜传感器观测曲线节选 器 [ J] .传感器技术 , 1998, 17(6):36-38. Fig 5　Observationcurveexcerptnorth-southtiltsensor [ 6] 　欧阳祖熙 , 张宗润 , 何成平 .基于 感应耦合比率臂 的高精度 位 4　结　论 电容式倾斜传感 器灵敏度高(2 ×10 -4 ″)、线性好、预调 节动态范围大, 能 够很 好地满 足深 井安装 的要 求。 将其 集 成在深井地壳形变宽频带多分量的综合观测 系统里。 在福建 移测量系统[ J] .电子技术应用 , 2004(4):41-43. 作者简介 : 吴立恒 (1980-), 女 , 浙江宁 波人 , 硕士 , 助 理研 究员 , 主要 从 事地震前兆仪器传感器的研究 。 (上接第 118页) 机器人运动 学算 法, 并作 了相 应的 测试, 结 果表 明 基于 牛 顿 —拉夫逊迭代法的逆 运动学 算法能 够在满 足实 时性要 求 的前提下达到较高的 精度, 具有较好的实用性。 参考文献 : [ 1] 　王 　浩 , 谢存禧 .基于回 转变换 张量的 6R机 器人 运动 学研 究 [ J] .厦门大学学报 , 2005, 9:640-644. [ 2] 　于艳秋 , 廖启征 .基于有理数运算的一般 6R机器人位置逆解 算法 [ J] .机械工程学报 , 2005, 41(3):229-233. [ 3] 　程永伦 , 朱世强 , 刘松国 .基于旋转 子矩阵正 交的 6R机 器人 运动学逆解研究 [ J] .机器人 , 2008, 3:160 -164. [ 4] 　刘松国 , 朱世强 , 王宣银 .基于矩阵分解的一般机器人 实时高 精度逆运动学算法 [ J] .机械 工程学报 , 2008, 11(11):304 - 309. rithmfortheinversekinematicsofageneralserial6Rmanipula- tor[ J] .MechanismandMachineTheory:2007, 42(1):66 -81. [ 6] 　LeeHY, LiangCG.Anewvectortheoryfortheanalysisofspa- tialmechanisms[ J] .Mechanism and MachineTheory, 1988, 23(3):209-217. [ 7] 　金媛媛 , 秦 　伟 .机器人逆 运动学的模拟退 火自适应遗传 算 法 [ J] .机械与电子 , 2007(1):31-38. [ 8] 　谭 　营 , 何振亚 , 邓 　超 .一种机器人逆运动学求解的神经 网 络方法 [ J] .电子科技大学学报 , 1998(3):310-314. [ 9] 　YangSX, MengM.Anefficientneuralnetworkmethodforreal- timemotionplanningwithsafetyconsideration[ J] .Roboticsand AutonomousSystem, 2000, 32:115-128. 作者简介 : 王 　宪 (1955-), 男 , 江苏无锡人 , 学士 , 高级工程师 。 研究 领 [ 5] 　ManfredLH, MartinP, Hans-PeterS.Anewandefficientalgo- 域为智能控制系统 , 现场总线 。