基于FPGA的伺服电机控制器.pdf-资料库

FPGA Realization of a High-performance Servo Controller for PMSM Zhaoyong Zhou and Tiecai Li Department of Electrical Engineering Harbin Institute of Technology Harbin, China E-mail: zhouzy@hit.edu.cn Abstract—This paper proposes a fully digitized hardware design scheme of a vector-controlled servo controller, which is verified and implemented on one-chip field programmable gate arrays (FPGA), for high-performance servo drives of the permanent magnet synchronous motor (PMSM). This scheme integrates the vector control strategy, the M/T speed measurement algorithm, the PI regulating technique and the SVPWM principle as well as the EDA design methodology, and it will be a good substitute for traditional PMSM drives practice. The realized control IC also contains a standard host communication interface, which enables the on-line configuration for all kinds of control parameters. The actual sample frequencies of the torque loop and the speed loop are limited by the selected FPGA; with respect to the Altera FPGA prototype mentioned in this paper, the two loops can respectively obtain a sample frequency of 40kHz and 20kHz as well as a bandwidth of 5kHz and 400Hz. Experimental results indicate that the controller can provide a controllable speed range from 0.2 RPM to 10,000 RPM with satisfactory dynamic and static performances. Keywords-vector control; servo; FPGA; PMSM I. INTRODUCTION High performance AC servo drive depends on the well control of the currents; however, the strong coupling and nonlinear natures of the AC motors make it impossible to directly control the stator currents to obtain the desired performances as the behavior of DC motors. Hence, a specific algorithm must be introduced to realize the decoupling of relevant variables. Fortunately this problem has been resolved by the vector control technology. The principle of vector control, often referred to as field-oriented-control, was first proposed by F. Blaschke of Siemens in the early 1970s for controlling induction motors, and after several years of efforts this method had been developed into a complete theory system [1], [2]. In the latest twenty years, the vector control technology has been used wider and wider in high performance AC drives due to the rapid progress in power electronics, computer and microelectronics. In engineering practice, because of the complexity of servo control algorithm, it is basically implemented with software based on DSP [3]; this approach can provide a flexible skill, but suffers from a long period of development and exhausts many resources of the CPU. In some cases, dual DSPs have to be adopted to achieve superior performances [4]. Toshio Takahashi and Eddy Ho Digital Control IC Design Center International Rectifier California, USA E-mail: ttakaha1@irf.com technology implementation In recent years, a novel design methodology has arisen, that is FPGA-based hardware [5]. Compared with ASIC, FPGA is only a collection of standard cells, which have none of specific functions, but owing to its field programmable characteristics and reuse of the IP cores, user can design his own ASIC according to their schemes with professional placement and routing tools in a shortest time, instead of participation of the semiconductor manufacturers. In addition, since FPGA can carry out parallel processing by means of hardware mode, which occupies nothing of the CPU, the system can get a very high speed level as well as an exciting precision. This new design methodology has been used in high performance motion control field, such as [6]-[8], which realize different current controller. In [6], the designed digital current controller integrates both nonlinear ∆ modulator and linear PI regulator and can obtain a very high bandwidth. Literature [7] provides a co-processor scheme based on the indirect vector control with current feed forward, and literature [8] proposes a digital hardware implementation where it can operate under different instructions. All these digital current controllers have achieved very high performances, however, it is obvious that these schemes have a common property that the current is considered as a co-processor and the speed or position control is implemented by DSP. As known to all, position control is very flexible and difficult to generalize, but the speed control is universal just as the current control, and high performance speed control can be impossible without the current control. Thus, it is necessary to integrate the speed and the current into a single chip, which can be separately used as a speed controller or a current controller; furthermore, the two controllers can also be incorporated into a position control system, as shown in Fig.1. If the FPGA has integrated CPU, the position, speed and current control can be all implemented with only one single chip, which will lead to a real SOC (system on a chip), the important trend of high performance motion control integration design. This paper studies the current vector control, PI regulation, feed back speed measurement and space vector PWM, and presents their digital structures. These algorithms are designed in International Rectifier iMOTION products such as the IRMCK201/IRMCK202 digital control ICs, and being applied to the real industry application. In detail, it is organized as follows. In section II, vector control principle of the PMSM is briefly reviewed and the relevant expressions are derived. 0-7803-8269-2/04/$17.00 (C) 2004 IEEE. 1604

Section III describes the design scheme of the digital hardware. Section IV implements the circuits on an Altera FPGA and shows the experimental results. In section V some conclusions are drawn. II. BASIC PRINCIPLE OF THE ROTOR-FLUX-ORIENTED VECTOR CONTROL For a PMSM with surface-mounted magnets that generate a constant flux-linkage with the stator windings, the typical vector control is the rotor-flux-oriented version. In Fig.2, the α- axis of the stationary reference frame is fixed to the axis of the A-phase stator winding, and the d-axis of the rotating reference frame is fixed to the direction of the rotor flux, which rotates at the electrical angular speed ω; θ is the angle between the d-axis and the α-axis, and . d /θω= dt The current space vector of the stator windings can be defined as =r i s i sα + ji sβ = + ai sB + 2 ia sC sA ) ( i 2 3 (1) j 2 3 π , a = e π j 4 3 2 a = e where isA, isB and isC are the instantaneous phase currents of the stator; isα and isβ are the two components of in the α-β reference frame. Under this definition, the projection of to every phase-axis is equal to the instantaneous current of the same phase. sir sir For a three-phase balanced system, the zero sequence component of the currents is equal to zero, i.e., Thus, we can obtain the Clarke transformation from three- i sA + i sB + i sC = 0 phase to two-phase as follows i sα i sβ     = = i sA i ( sB − i sC 3/) (2) If expressed in d-q reference frame, the current space vector can be rewritten as + r =′ i s ji i sd (3) where isd and isq are the two components of in d-q reference frame. From (3), a transformation from the stationary reference frame to the rotating reference frame can be obtained as si ′r sq −⋅= r θjei s i sd i sq     = i sα −= i sα θ + i cos sβ θ + i sin sβ θ sin (4) θ cos and the transformation from the rotating reference frame to the stationary reference frame can be expressed as i sα i sβ     = = i sd i sd cos sin θ − i sq θ + i sq sin cos θ (5) θ The electromagnetic torque can be expressed as Figure 1. Integrated Architecture of AC Servo System Figure 2. Reference Frames for Vector Control where P is the pole pairs and is the constant flux-linkage with the stator windings due to the permanent magnets. Fψ It follows from (6) that the electromagnetic torque can be controlled independently by isq. This is the essential point of the rotor-flux-oriented vector control for the PMSM. To realize the vector control strategy, a series of coordinate transfor- mation must be carried out. III. DESIGN SCHEME FOR THE DIGITAL HARDWARE Fig.3 is the data path of the speed servo controller. It consists of several function modules, such as Clarke transformation module, vector rotating transformation module, PI regulator module, space vector PWM module, M/T speed measurement module, DC-link voltage compensation module and scaling module, etc. In this part, only the main modules are discussed. A. Vector transformation module to the rotating Vector transformation includes phase transformation and rotating transformation. Expression (2) gives the Clarke phase transformation, which can be implemented with an adder and a multiplier. With respect transformation expressed by (4) and (5), traditionally they are computed by look up table or Tailor series, but the two methods are not ideal. In fact, there is another excellent algorithm called CORDIC (Coordinate Rotation Digital Computer) which can only use shift and add/subtract operations to realize vector rotating transformation with a wonderful result, including high speed and high resolution [9]. Moreover, the CORDIC algorithm is very qualified for hardware implementation [10]. , [ ππθ −∈ ] If ，the following vector rotation θje = r xV ( in r V out out out y y ⋅ ) ( x in , in ) , T e ψ= P i sqF 3 2 (6) can be realized using CORDIC algorithm, which needs only 1605

Figure 3. Data Path of the Speed Servo Controller + nI ][ nP ][ ⋅ Error n ][ nOut ][ = where the proportional term is K nP ][ and the integral term is +− ]1 nI ][ nI [ K = = p − + 1 = = x i y x i y − + shift and add operations. The iterative equations of CORDIC are expressed as         d  i   ⋅ d y i i ⋅ xd i i ∑ d = k 0 ) , + 1 = z sgn( ,2,1,0 arctan( − k )2 2 2 i = L ⋅ ⋅ + 1 − − = n 1 z z − ⋅ 0 k i i i i i i i where = d i sgn( z ) i = z i ≥ z i 0 < 0 ,1 ,1   −  in y      x 0 y z −= = sgn( θ −= The initial values are defined as θ ⋅ sgn( ) θ ⋅ x ) in θ ⋅ 90) sgn( It provides the following result: y y sin cos cos sin in 0 0 in x n y z n n      = = → xA ( n in xA ( n 0 in − θ + θ ° θ ) θ ) = = xA n yA n out out This algorithm introduces a gain as follows n ∏− = 0 where n is large enough. 1 = A n K = n i 1 + 21 − 2 ≈ i .1 646760258 The CORDIC hardware structure is shown in Fig.4. B. PI regulator module Both the current and the speed are adjusted by the digital PI law based on the bilinear transformation, which is formulated as 1606 ⋅ x ( Error n ][ + Error [ n − ])1 Error[n] is the error input, and Kp, Kx are the proportional and integral gains, respectively. The hardware structure of the PI regulator is shown in Fig.5. In order to prevent overflow, the regulator has setup a saturation limit. The output of the current PI regulator is a voltage modulation index command, which is sent to the SVPWM module after compensated; the output of the speed PI regulator is a current reference command which is directly sent to the current PI regulator. If the command has a very large value, the integrator will probably establish an excessive error value, and because of the inertial property of the integrator, this large error may keep a long time and result in unwanted overshoot. Thus, the output of the integrator should be limited to a certain value when design the PI regulator and once the output exceeds the limit, the integrating behavior will stop immediately so as to reduce the overshoot. This process is called anti-windup. C. Speed measurement module In the servo system, a key problem is the measurement of the rotor position and speed. This scheme adopts incremental encoder and switching Hall sensors to detect the position of the rotor. When power is on, the Hall sensors detect a coarse initial position that can be used to softly start the motor, and an accurate position will be obtained as soon as the Z pulse of the encoder occurs. Before the quadrature pulses of the encoder arrives the processor, their frequencies are quadruplied. The feedback speed measurement is accomplished using M/T method, which is suitable for both high speed and low speed measurement, as shown in Fig.6. Assume that the number N corresponds to the maximal

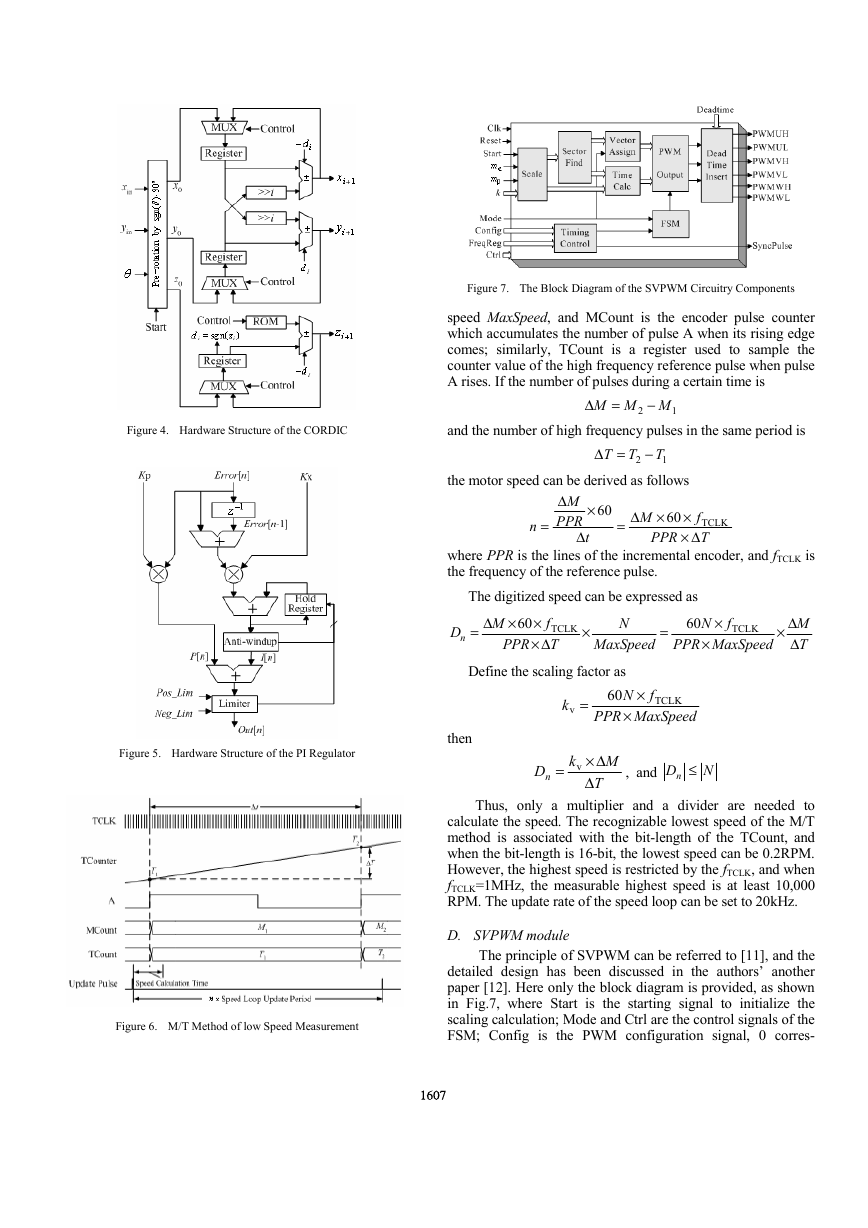
Figure 7. The Block Diagram of the SVPWM Circuitry Components speed MaxSpeed, and MCount is the encoder pulse counter which accumulates the number of pulse A when its rising edge comes; similarly, TCount is a register used to sample the counter value of the high frequency reference pulse when pulse A rises. If the number of pulses during a certain time is and the number of high frequency pulses in the same period is the motor speed can be derived as follows 2 MMM − 2 T T 1 =∆ T ∆ − = 1 = n ∆ M PPR ∆ t × 60 ×∆= M 60 PPR × f TCLK ∆× T Figure 4. Hardware Structure of the CORDIC where PPR is the lines of the incremental encoder, and fTCLK is the frequency of the reference pulse. The digitized speed can be expressed as ×∆= M 60 60 PPR PPR × f TCLK ∆× T MaxSpeed N = × × fN × MaxSpeed TCLK Dn ∆× M ∆ T Define the scaling factor as 60 PPR = k v × fN × MaxSpeed TCLK Figure 5. Hardware Structure of the PI Regulator then k = v Dn M ∆× ∆ T , and Dn ≤ N Thus, only a multiplier and a divider are needed to calculate the speed. The recognizable lowest speed of the M/T method is associated with the bit-length of the TCount, and when the bit-length is 16-bit, the lowest speed can be 0.2RPM. However, the highest speed is restricted by the fTCLK, and when fTCLK=1MHz, the measurable highest speed is at least 10,000 RPM. The update rate of the speed loop can be set to 20kHz. D. SVPWM module The principle of SVPWM can be referred to [11], and the detailed design has been discussed in the authors’ another paper [12]. Here only the block diagram is provided, as shown in Fig.7, where Start is the starting signal to initialize the scaling calculation; Mode and Ctrl are the control signals of the FSM; Config is the PWM configuration signal, 0 corres- Figure 6. M/T Method of low Speed Measurement 1607

ponding to the asymmetrical mode and 1 corresponding to the symmetrical mode; mα and mβ are the modulation indexes in stationary reference frame coming from the digital current PI regulator; k is the scaling factor to transform the indexes to time values; FreqReg is the switching frequency register. Besides the above modules, there are other auxiliary function modules, such as communication, configuration and status register file, monitor and protection, etc. All these modules constitute a complete single-chip servo controller. IV. FPGA IMPLEMENTATION AND EXPERIMENTAL RESULTS Each module of the servo controller is described with Verilog HDL and synthesized with Synplify® software. After placement and routing in Quartus II environment, the controller IC is implemented on one-chip Altera Cyclone EP1C20F400 FPGA, and the total ATOM counts for this design are about 7492 of total 20060 (37%). The design summary is given in Table I. The designed IC can operate at 40MHz system clock, and all kinds of control parameters can be accessed via the communication port on-line by a host. This IC can be considered as either a slave device that can interface with the DSP and other circuits to construct a complete position servo control system, or an IP core which can be integrated into a motion control SOC with the IP core of CPU. This SOC style of motion control can greatly reduce the area of a PCB of the whole system and improve its immunity to interferences. 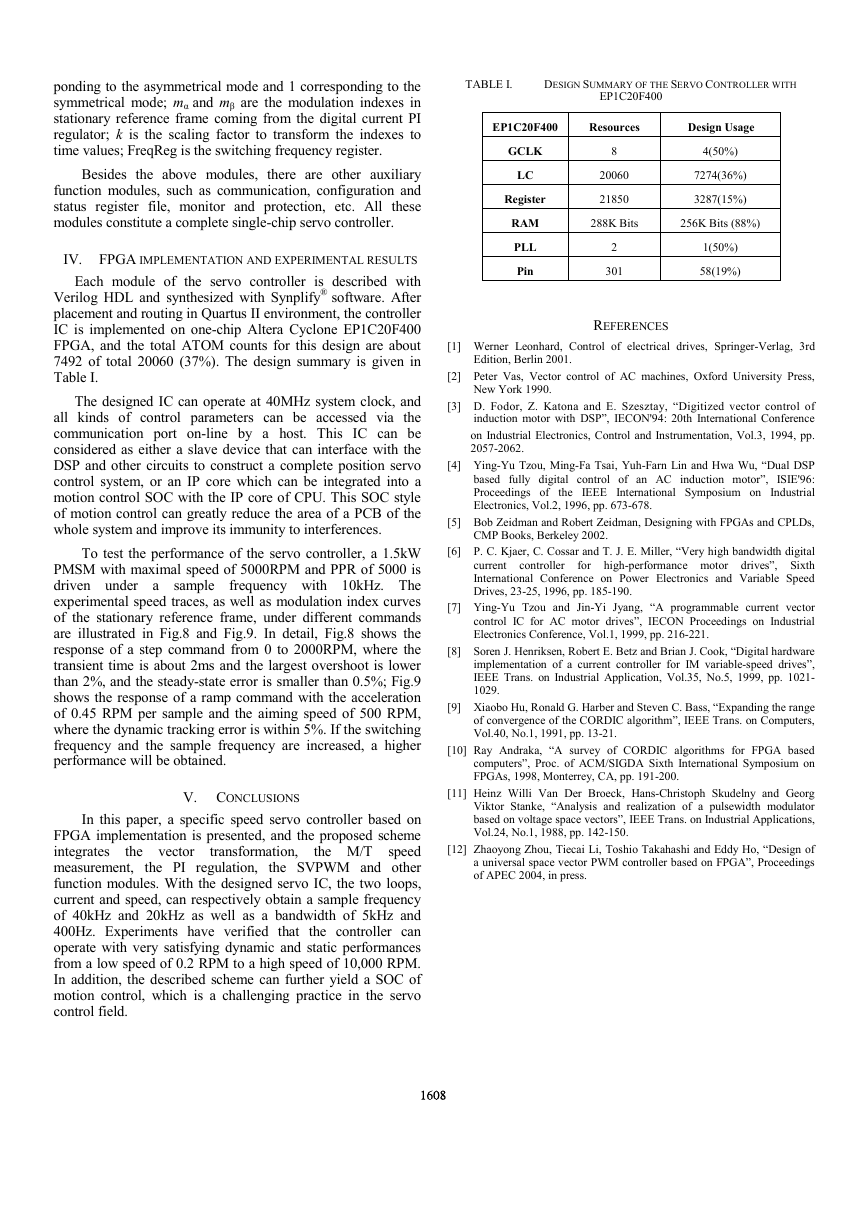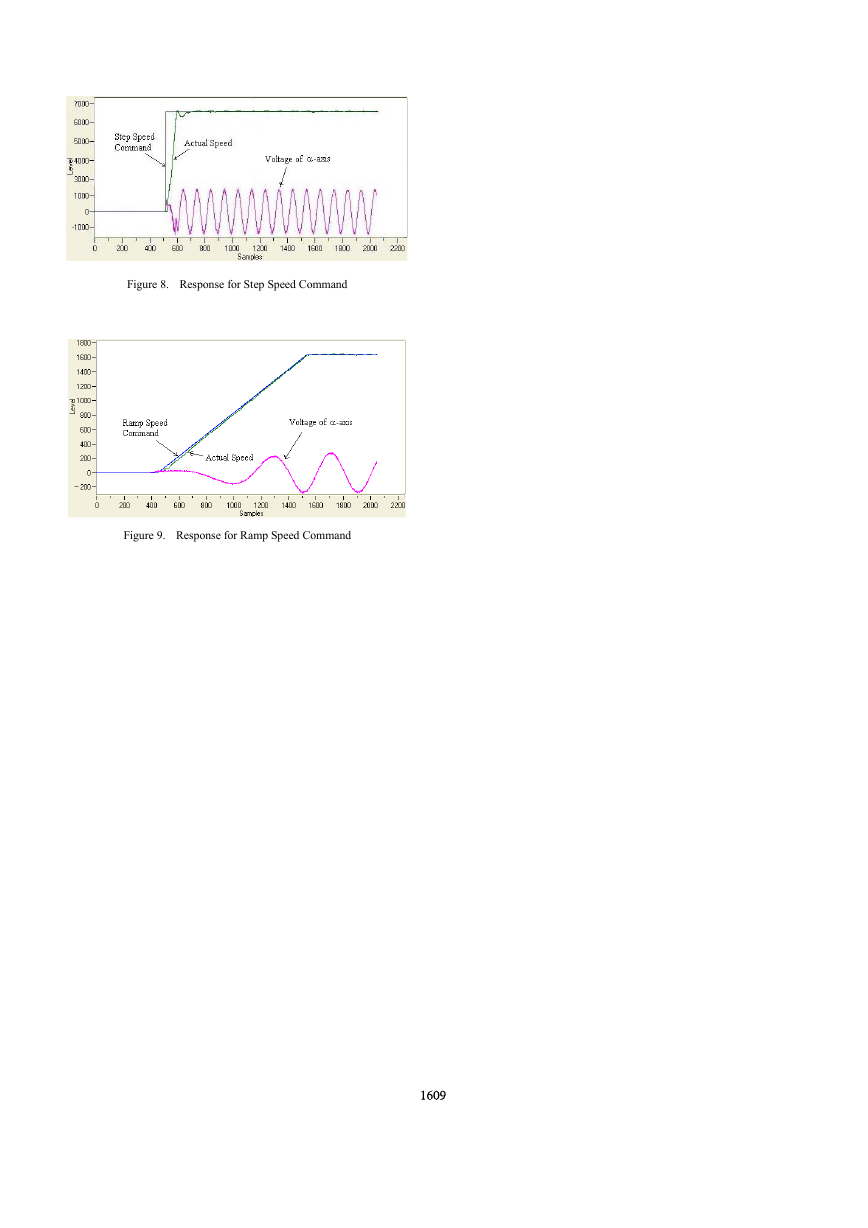To test the performance of the servo controller, a 1.5kW PMSM with maximal speed of 5000RPM and PPR of 5000 is driven under a sample frequency with 10kHz. The experimental speed traces, as well as modulation index curves of the stationary reference frame, under different commands are illustrated in Fig.8 and Fig.9. In detail, Fig.8 shows the response of a step command from 0 to 2000RPM, where the transient time is about 2ms and the largest overshoot is lower than 2%, and the steady-state error is smaller than 0.5%; Fig.9 shows the response of a ramp command with the acceleration of 0.45 RPM per sample and the aiming speed of 500 RPM, where the dynamic tracking error is within 5%. If the switching frequency and the sample frequency are increased, a higher performance will be obtained. V. CONCLUSIONS the M/T the vector transformation, In this paper, a specific speed servo controller based on FPGA implementation is presented, and the proposed scheme integrates speed measurement, the PI regulation, the SVPWM and other function modules. With the designed servo IC, the two loops, current and speed, can respectively obtain a sample frequency of 40kHz and 20kHz as well as a bandwidth of 5kHz and 400Hz. Experiments have verified that the controller can operate with very satisfying dynamic and static performances from a low speed of 0.2 RPM to a high speed of 10,000 RPM. In addition, the described scheme can further yield a SOC of motion control, which is a challenging practice in the servo control field. 1608 TABLE I. DESIGN SUMMARY OF THE SERVO CONTROLLER WITH EP1C20F400 EP1C20F400 Resources Design Usage GCLK LC Register RAM PLL Pin 8 20060 21850 4(50%) 7274(36%) 3287(15%) 288K Bits 256K Bits (88%) 2 301 1(50%) 58(19%) REFERENCES [1] Werner Leonhard, Control of electrical drives, Springer-Verlag, 3rd Edition, Berlin 2001. [2] Peter Vas, Vector control of AC machines, Oxford University Press, New York 1990. [3] D. Fodor, Z. Katona and E. Szesztay, “Digitized vector control of induction motor with DSP”, IECON'94: 20th International Conference on Industrial Electronics, Control and Instrumentation, Vol.3, 1994, pp. 2057-2062. [4] Ying-Yu Tzou, Ming-Fa Tsai, Yuh-Farn Lin and Hwa Wu, “Dual DSP based fully digital control of an AC induction motor”, ISIE'96: Proceedings of the IEEE International Symposium on Industrial Electronics, Vol.2, 1996, pp. 673-678. [5] Bob Zeidman and Robert Zeidman, Designing with FPGAs and CPLDs, CMP Books, Berkeley 2002. [6] P. C. Kjaer, C. Cossar and T. J. E. Miller, “Very high bandwidth digital current controller for high-performance motor drives”, Sixth International Conference on Power Electronics and Variable Speed Drives, 23-25, 1996, pp. 185-190. [7] Ying-Yu Tzou and Jin-Yi Jyang, “A programmable current vector control IC for AC motor drives”, IECON Proceedings on Industrial Electronics Conference, Vol.1, 1999, pp. 216-221. [8] Soren J. Henriksen, Robert E. Betz and Brian J. Cook, “Digital hardware implementation of a current controller for IM variable-speed drives”, IEEE Trans. on Industrial Application, Vol.35, No.5, 1999, pp. 1021- 1029. [9] Xiaobo Hu, Ronald G. Harber and Steven C. Bass, “Expanding the range of convergence of the CORDIC algorithm”, IEEE Trans. on Computers, Vol.40, No.1, 1991, pp. 13-21. [10] Ray Andraka, “A survey of CORDIC algorithms for FPGA based computers”, Proc. of ACM/SIGDA Sixth International Symposium on FPGAs, 1998, Monterrey, CA, pp. 191-200. [11] Heinz Willi Van Der Broeck, Hans-Christoph Skudelny and Georg Viktor Stanke, “Analysis and realization of a pulsewidth modulator based on voltage space vectors”, IEEE Trans. on Industrial Applications, Vol.24, No.1, 1988, pp. 142-150. [12] Zhaoyong Zhou, Tiecai Li, Toshio Takahashi and Eddy Ho, “Design of a universal space vector PWM controller based on FPGA”, Proceedings of APEC 2004, in press.

Figure 8. Response for Step Speed Command Figure 9. Response for Ramp Speed Command 1609

资料库

基于FPGA的伺服电机控制器.pdf

相关推荐

行业

热门标签

最新资料