灰色马尔科夫模型在城镇职工年平均收入预测中的应用.pdf

发布时间：2022-05-30 发布人：admin 分类：说明书资料大小：0.26M 资料格式：pdf 举报版权申诉

weixin_38562492-12103148-4744302542849263813.pdf-第1页.png

第1页 / 共8页

weixin_38562492-12103148-4744302542849263813.pdf-第2页.png

第2页 / 共8页

weixin_38562492-12103148-4744302542849263813.pdf-第3页.png

第3页 / 共8页

weixin_38562492-12103148-4744302542849263813.pdf-第4页.png

第4页 / 共8页

weixin_38562492-12103148-4744302542849263813.pdf-第5页.png

第5页 / 共8页

weixin_38562492-12103148-4744302542849263813.pdf-第6页.png

第6页 / 共8页

weixin_38562492-12103148-4744302542849263813.pdf-第7页.png

第7页 / 共8页

weixin_38562492-12103148-4744302542849263813.pdf-第8页.png

第8页 / 共8页

文本预览

中国科技论文在线 http://www.paper.edu.cn 灰色马尔科夫模型在城镇职工年平均收入预测中的应用李昊，钱存华** （南京工业大学经济与管理学院，南京 210009）摘要：本文对灰色预测模型的优点和不足进行了简要的分析说明,并基于马尔科夫链对灰色模型进行修正，建立了灰色马尔科夫预测模型。该模型既能体现灰色系统预测可用于复杂条件及少量原始数据的应用特点，又能利用马尔科夫模型对灰色模型的随机性进行修正，消除了传统灰色预测的固定偏差。利用 2004—2013 年的城镇职工平均工资数据对模型进行预测验证，结果显示灰色马尔科夫模型预测精度较高，其精度完全满足检验等级要求，该模型在城镇职工年平均收入的预测上具有较高的科学性和实用性。关键词：收入预测；灰色模型；马尔科夫链；精度检验中图分类号：O211.6 The prediction of average income for urban workers based on Grey Markov Model LI Hao, QIAN Cunhua (School of Economics &Management, Nanjing Tech University, Nanjing 210009) Abstract: In this paper, we make a brief analysis of advantages and disadvantages of the Grey Prediction Model, then repair the error by using Markov chain and set up Grey Markov model. This model can be used in the complex environment with less date, also it can offers the opportunity to correct the problem of randomness and erase the biases. By using the date of the urban workers’ average income from 2004 to 2013. We can test the Grey Markov model and proved that it meet the requirement of accuracy. So this model can be used in the prediction of average income for urban workers, which has a certain practicability and reference value. Key words: revenue forecasting; Grey model; Markov chain; accuracy test 0 引言城镇职工工资是城镇居民收入的重要组成部分，是衡量城镇居民生活水平的重要标准，也是国家制定相关政策和发展战略的重要依据，因此，对城镇职工平均工资的预测是具有切实意义的[1]。由于受国家政策法规和宏观经济发展状况等多种因素的影响，城镇职工收入的发展趋势是呈高度非线性的，因此预 5 10 15 20 25 30 测难度较大，精度无法保证。 35 灰色系统理论是由我国著名学者邓聚龙教授于 1982 年创立，是一门“以部分信息已知，部分信息未知的小样本、贫信息”不确定性系统为研究对象的系统科学新学科。灰色系统理论认为：任何随机过程都可看作一定时间区域变化的灰色变量，通过生成变换可将无规律序列变成有规律序列[2]。灰色系统理论的基础与核心是传统的 GM(1，1)模型（Grey Model)，它主要适用于时间短，数据资料少且随机波动不大的系统现象，对于随机性波动较大的数列进行预测，作者简介：李昊（1989-），男，硕士研究生，主要研究方向：随机过程，养老政策研究通信联系人：钱存华（1964-），男，教授，硕士生导师，主要研究方向：可靠性数学，随机过程，企业生产管理，供应链管理. E-mail: qch64317@njtech.edu.cn 40 - 1 -

中国科技论文在线 http://www.paper.edu.cn 其预测值就会偏低或偏高，拟合较差，预测精度不理想。马尔科夫过程是一种具有“马尔科夫性”的随机过程。马尔科夫性即无后效性，是指当过程在时刻 T0 所处的状态为已知时，过程在 T0 时刻以后所处的状态只与 T0 时刻所处状态有关，与 T0 时刻以前所处的状态无关。即“已知现在，将来与过去无关。”因此马尔科夫转移概率预测可以揭示系统在波动的不同状态区间转移的内在规律，修正系统因各种随机作用而产生的波动[3]。但用马尔科夫链进行数据分析必须掌握大量的历史数据，且单纯的马尔科夫预测要求其预测对象具有马氏链和平稳过程的特点，这与经济预测问题是大量地随时间变化而呈现某种变化趋势的非平稳随机过程不符。针对灰色模型在长期预测时，数据序列拟合较差，预测精度偏低；而马尔科夫链适用于长期、数据序列随机波动大的模型的特点，可以建立混合的灰色马尔科夫预测模型来对数据进行预测处理。即通过灰色系统理论对数据进行预测，然后通过马尔科夫链还原数据的随机性，修复预测数据误差从而达到更高的预测精度。基于灰色马尔科夫模型的多种优势，该模型被广泛运用于人口数量、工业参数、事故概率或生态环境等多种复杂数据的预测[4-7]。本文依据近年来我国城镇职工的收入特征，建立了灰色马尔科夫预测模型并对城镇职工年平均工资进行了预测。所建模型通过了精度检验，具有较高的预测精度，其预测 45 50 55 结果基本上反映了我国城镇职工年平均工资的发展趋势。 1 灰色模型 60 1.1 灰色模型建立及求解在建立 GM(1，1)模型之前，需要弱化原始时间序列的随机性，从而为建立灰色模型提供数据信息，因此要对数据做累计生成序列。假设原始时间序列为： X )0(  X  )0( 1 , X )0( 2 ,..., )0( nX 65 对原始数据进行累加 X )1( k   k 1 X )0( i  k , ,...2,1 n  则累加生成序列为 )1( X   X )1( 1 , X )1( 2 ,..., )1( nX 然后对该生成序列建立如下微分方程： 70 dX )1( dt    X )1(  （1）其中：模型参数 α 称作发展灰度，μ 称作内生成控制灰度，该组数据为已知序列确定的常数，离散化后的微分方程参数估计的矩阵型式为： - 2 -

中国科技论文在线  ˆ ˆ   T http://www.paper.edu.cn （2）  YBBB T  1  T 其中： 75 BB  ( n 2)1              1 2 1 2 1 3   x x  x 1 1  x  2  2     x 1 1  1 n n 2   1     1        x  1  , Y  Y ( n )1   x 0 2 x 0 3  x 0 n               解得微分方程后可以得到该模型的时间响应函数为： ˆ x )1( k 1   x )0( 1    k           （3）然后经过一次累减就可以还原得到该模型的预测值函数为： ˆ x )0( k 1   ˆ x )1( k 1   ˆ x )1( k  ˆ x )0( 1      1          k  （4） 80 该拟合序列就是灰色模型所反映的原始数列的变化趋势。 1.2 灰色模型检验灰色预测模型检验一般包括残差检验，关联度检验和后验差检验。（1）残差检验：根据预测得来的数值，计算原始数列 X0 与预测值的绝对误差和相对误差，其计算公式为： X  J )0( H  J X )0( ˆ X  )0( i ,  ,2,1 n （5）  100 i %, 1,2,  n （6）（2）关联度检验：根据灰色模型的绝对误差，可以做预测序列与原始序列的关联度检验，根据以往经验 ρ 在这里一般取 0.5，当关联度大于 0.6 时模型精度即可保证，关联度的计算公式为： min J   J   max   （7） max   J    J  1 n  n i 1  85 90 （3）后验差检验：后验差检验主要的参考数据为均方差比值 C 以及小误差概率 P，设 SX 与 SJ 分别为原始数据和 J 的标准差，一般认为，当 C 小于 0.8 且 p 大于 0.6 时模型精度合格，其计算公式为： J X （8） C  S S - 3 -

中国科技论文在线 95  XPP  http://www.paper.edu.cn )0( ˆ X  )0(  674.0  XS （9）通过计算后，可以对模型精度进行评估，参考标准见模型检验等级分表：表 1：精度检验等级表精度等级相对误差关联度标准差比值小误差概率一级二级三级四级 0.01 0.05 0.10 0.20 2 马尔科夫预测模型 2.1 马尔科夫链定义解 0.9 0.8 0.7 0.6 0.35 0.5 0.65 0.8 0.95 0.80 0.70 0.60 100 假设随机过程序列{Xn, n≥0}，对于任意的 n≥1，任意非负整数 i1，i2，… in， i，j∈E，恒有  XP  Xj |  0 i 0 , , X  n 1   i , X n n 1  n 1    i  XP  Xj | n n 1  i  则称{Xn，n≥0}为马尔科夫链，如果 N 为可离散集和，则称{Xn，n≥0}为离散参数的马尔科夫链。 105 设 I 为离散参数的马尔科夫链的状态空间，则称条件概率 Pij 为序列的 n 步转移概率，即从状态 i 转移到状态 j 的概率；若转移概率与时间起点 m 无关，称此马尔科夫链为非齐次马尔科夫链，其状态转移矩阵可以表示为： P 11 P 21  P n 1       矩阵中元素非负，行和为 1。 110 2.2 状态划分及数据修正 P 12 P 22 P n 1 P 2 n    P P n nn  2       把一个具有马尔科夫性的非平稳随机序列   kY i=1，2，3…n。任意状态表示为 Qi=[Q1i，Q2i]，其中  划分为 n 个状态 Qi， 0ˆkx Q 1 i Q 2 i   kY   kY   yA i yB i 115 灰元 Q1i、Q2i 随时间 t 变化而变化，划分状态数 s 和 Ai、Bi 可由预测值和具体情况而定，其中为原始数据均值。以 Ni 表示处于 i 状态的频数，Nij 表示由状 - 4 -

中国科技论文在线 http://www.paper.edu.cn 态 i 经过一步转移到状态 j 的频数，从而求出一步转移概率矩阵： P  ij N ij N i （10） 120 若预测序列目前处于 Qi 状态，则考察 P 所处的第 i 行，若 pij 为该行的最大值，则下一时最有可能转向状态 Qj。如果 P 中第 i 行有两个或两个以上的概率值相同或接近，则采用加权平均法计算。确定了未来序列变动的灰区间[Q1i，Q2i] 后，可用区间中位数来作为最终的预测值 G(k)。 1 2 （11）   kG   kY yB  Q i 1 1 2 A i Q        2 i i 3 城镇职工平均工资预测 125 3.1 建立 GM(1，1)模型并求解本文基于中国统计年鉴，选取 2004 年到 2013 年城镇职工平均工资进行模拟计算，原数据见表 4（数据来源于《中国统计年鉴 2014》）。假设 0ˆ kX 为城镇企业职工平均工资预测值，利用 MATLAB 软件按照公式（2）， 130 T ˆ  .0 12593  ˆ  可以分别计算求出  （4），即可得到城镇企业职工的平均工资的计算公式为 [8-10] 3.2 状态划分 16047 69. T ，将所得数据代入公式 ˆ kx )0(  1 16962  .0 12393 k 。马尔科夫预测根据每年实际值状态变化来确定状态转移概率矩阵从而确定预测值的方法，故先把实际值按照相对误差进行划分，对于在职职工人口预测 135 数据，本文选取四个状态区间：表 2：各个状态取值范围状态 1 2 3 4 1.1%~2.9% y .0 047 -0.1%~1.1%   kY    kY   kY   kY 011.0 029.0 001 .0    y y y     取值范围 -5.8%~-4.7% -4.7%~-0.1% 1 : QQ 11 QQ 2 21 QQ 31 : : 3 140 QQ : 4 41 各年份所处状态：       kY   kY   kY   kY  .0 058 y ,  .0 047 y , Q 12 Q 22  001.0 y , Q 32  011.0 y , Q 42 - 5 -

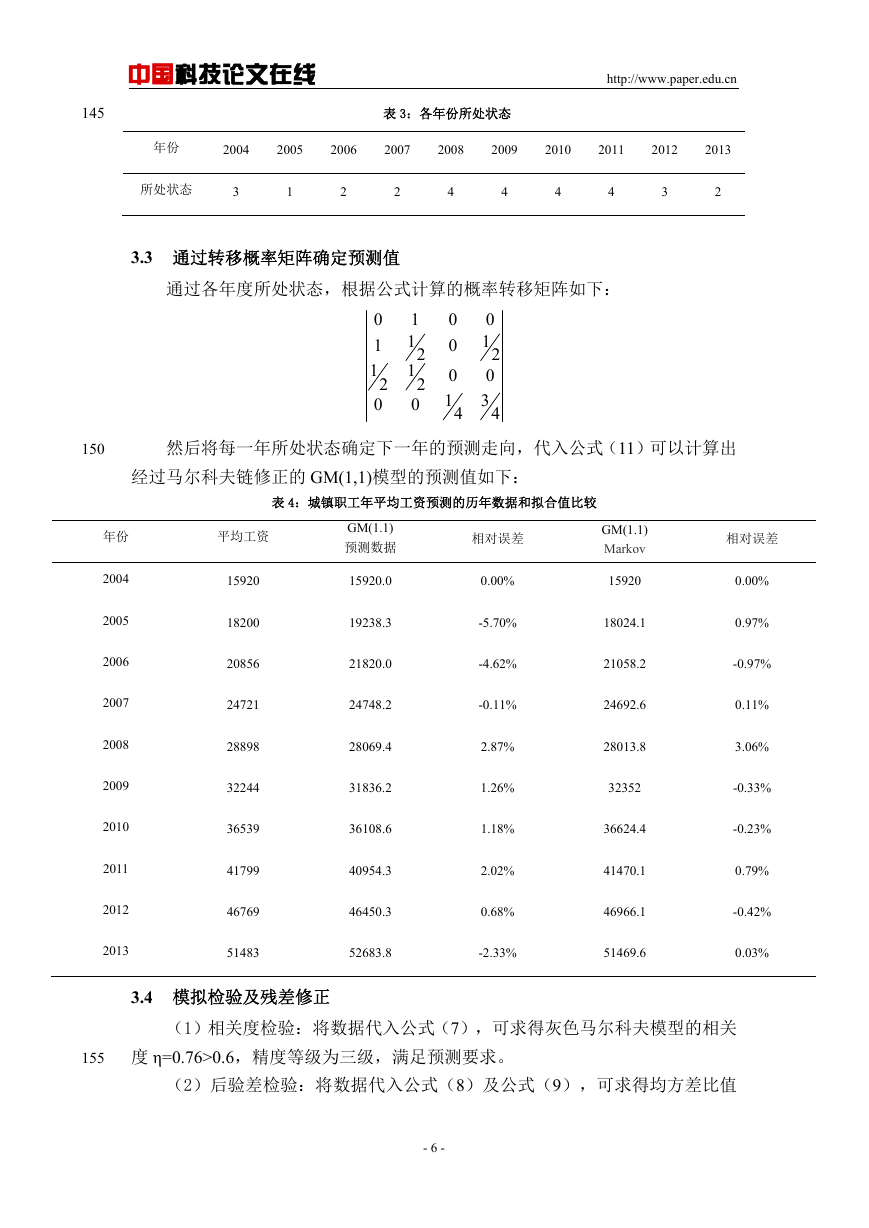
中国科技论文在线 http://www.paper.edu.cn 145 表 3：各年份所处状态年份所处状态 2004 2005 2006 2007 2008 2009 2010 2011 2012 2013 3 1 2 2 4 4 4 4 3 2 3.3 通过转移概率矩阵确定预测值通过各年度所处状态，根据公式计算的概率转移矩阵如下： 0 1 1 2 0 1 1 2 1 2 0 0 0 0 1 4 0 1 2 0 3 4 150 然后将每一年所处状态确定下一年的预测走向，代入公式（11）可以计算出经过马尔科夫链修正的 GM(1,1)模型的预测值如下：表 4：城镇职工年平均工资预测的历年数据和拟合值比较年份平均工资 GM(1.1) 预测数据相对误差 2004 2005 2006 2007 2008 2009 2010 2011 2012 2013 15920 18200 20856 24721 28898 32244 36539 41799 46769 51483 15920.0 19238.3 21820.0 24748.2 28069.4 31836.2 36108.6 40954.3 46450.3 52683.8 0.00% -5.70% -4.62% -0.11% 2.87% 1.26% 1.18% 2.02% 0.68% -2.33% GM(1.1) Markov 15920 18024.1 21058.2 24692.6 28013.8 32352 36624.4 41470.1 46966.1 51469.6 相对误差 0.00% 0.97% -0.97% 0.11% 3.06% -0.33% -0.23% 0.79% -0.42% 0.03% 3.4 模拟检验及残差修正（1）相关度检验：将数据代入公式（7），可求得灰色马尔科夫模型的相关 155 度 η=0.76>0.6，精度等级为三级，满足预测要求。（2）后验差检验：将数据代入公式（8）及公式（9），可求得均方差比值 - 6 -

中国科技论文在线 http://www.paper.edu.cn C=0.021<0.35，小误差概率 P=1>0.95，精度等级均为一级，精度比较高。（3）残差检验：经马尔科夫链修正后的预测结果相对误差值较原来有较大改善，误差均值小于 0.007<0.01，均在 0.05 的范围之内，精度等级为一级。 160 因此，该模型精度可靠，完全满足预测要求。我们可以根据该方法模拟计算出 2014 年城镇职工平均工资并进行数据修正，预测结果为 59698.2，也可以基于灰色模型对 2015—2019 年的数据进行简单预测，预测结果见表 5：表 5：城镇职工年平均工资预测年份 2014 2015 2016 2017 2018 2019 预测数据 59698.2 67998.8 77022.4 87240.0 98906.2 112190.3 4 结论 165 本通过对基于灰色理论所建立的城镇职工平均工资预测模型进行马尔科夫修正，我们可以有效地克服随机波动性较大的数据对预测结果的造成的影响，预测误差也比单纯使用灰色模型误差小，预测精度得到了有效提高，可以很好地反映我国城镇职工的收入情况以及总体变化趋势，其实际效用是可行的。 170 根据预测，至2019 年我国城镇职工年平均收入将超过10 万元，相对于2013 年平均收入翻一番，工资年平均增长率超过 13.4%，因此可以认定我国在未来 5 年经济依然处于高速发展阶段，城市化进程也会不断加快，因此，为确保我国经济的可持续发展，急需制定正确的宏观经济战略方针。本文的预测数据基于近十年来的历史数据，预测模拟效果较好，能为国民经济计划的制定和社会战 175 略目标的实现提供数据支援，具有一定的切实意义。 [参考文献] (References) 180 [1] 秦凯; 季晓晶; 王作东. 城镇居民增收因素及潜力实证研究[J]. 统计研究, 2010(07):102-104. [2] 邓聚龙. 灰色系统基本方法[M]. 武汉:华中理工大学出版社, 1988. [3] 汪荣鑫. 随机过程[M]. 西安:西安交通大学出版社, 1987. [4] 卞焕清. 基于灰色马尔可夫链模型的人口预测[J]. 数学的实践与认识, 2012(07):127-132. [5] 顾央青. 基于无偏灰色马尔科夫模型的物流需求量预测[J]. 物流技术, 2013(21):262-268. [6] 王永刚;吕学梅. 民航事故征候的灰色马尔可夫预测 [J]. 安全与环境学报, 2008(01):163-165. - 7 -

中国科技论文在线 http://www.paper.edu.cn 185 [7] 杨锦伟;孙宝磊. 基于灰色马尔科夫模型的平顶山市空气污染物浓度预测 [J]. 数学的实践与认识, 2014(02):66-70. [8] 陈树德. 灰色模型的简化计算[J]. 徐州工程学院学报(自然科学版), 2009(04):58-64. [9] 王学萌. 灰色系统分析及实用计算程序[M]. 武汉:华中理工大学出版社, 2001. [10] 杨旭. 改进的灰色预测 GM(1,1)模型的 MATLAB 实现 [J]. 江苏科技信息, 2014(07):69-70. - 8 -

分享到：

赞收藏

资料库

灰色马尔科夫模型在城镇职工年平均收入预测中的应用.pdf

相关推荐

开发技术

热门标签

最新资料