一种解潮流问题的矢量化复数牛顿法.pdf

发布时间：2022-05-29 发布人：admin 分类：说明书资料大小：0.22M 资料格式：pdf 举报版权申诉

weixin_38733597-12122255-A201004-128.pdf-第1页.png

第1页 / 共9页

weixin_38733597-12122255-A201004-128.pdf-第2页.png

第2页 / 共9页

weixin_38733597-12122255-A201004-128.pdf-第3页.png

第3页 / 共9页

weixin_38733597-12122255-A201004-128.pdf-第4页.png

第4页 / 共9页

weixin_38733597-12122255-A201004-128.pdf-第5页.png

第5页 / 共9页

weixin_38733597-12122255-A201004-128.pdf-第6页.png

第6页 / 共9页

weixin_38733597-12122255-A201004-128.pdf-第7页.png

第7页 / 共9页

weixin_38733597-12122255-A201004-128.pdf-第8页.png

第8页 / 共9页

文本预览

中国科技论文在线 http://www.paper.edu.cn 一种解潮流问题的矢量化复数牛顿法1 龙丹丽，韦化广西大学电气工程学院，南宁（530004） E-mail: longdanli@163.com 摘要：电力系统潮流计算是确定整个电力系统各部分运行状况的重要手段，用以定量分析比较供电方案或运行方式的合理性。本文区别于过去潮流计算中将视在功率展开成有功和无功来处理的做法，直接将整个潮流模型全部变为简练的复数形式，极大缩减了求解潮流问题计算规模。方法分析了复数形式下的极坐标潮流模型，具体给出了不平衡复功率的计算、雅克比矩阵的形成以及平衡节点和 PV 节点的处理方法；运用了精妙的矢量化技术编程实现。多个系统的仿真测试结果表明，复数求解方法更简洁、资源使用效率更高。关键词：复数潮流模型；矢量化运算；极坐标牛顿法；电力系统潮流计算中图分类号：TM761 1 引言电力系统潮流计算是电力系统各种问题中投入研究力量最多的领域之一。它可归结为求解多元非线性代数方程组的问题，目前广泛采用的是牛顿法[1]。在理论上，FDPF[2]、IM 法 [3]、各种鲁棒处理方法[4]-[9]等大量基于牛顿法的处理技术已被研究应用，更有科学家提出由于牛顿法与一组独立的常微分方程可形式类推，任何有效的数值积分方法都可用来求解潮流问题[10]，良好的收敛性已不是我们担心的内容。迄今为止，传统的极坐标潮流计算是以各母线的电压幅值和功角作为变量，分别列出有功功率和无功功率的平衡方程，然后利用牛顿法迭代求解修正方程求出变量[11][12]。此时模型中变量是系统规模的两倍，这对于大系统的应用无疑使得计算量庞大。从巨型计算电路板到数字计算机，硬件机器的发展推动了电力系统潮流计算速度的提高。自从 19 世纪 60 年代 Bill Tinney[13]阐释了稀疏矩阵，稀疏技术逐渐被应用到了电力系统潮流分析中，使计算效率大幅提高。文献[14]中提出了采用矢量化的方法，对简化潮流分析工程的程序加速开发进程有显著成效。基于上面的讨论可见，随着电力系统变得日益庞大和复杂，潮流计算的计算量也越来越大，如何充分利用先进的数字硬件和软件资源来进行是潮流分析才是如今的研究趋势。因此我们把研究目光放在牛顿法潮流分析的以下几方面：由于极坐标模型与混合极坐标、混合直角坐标和直角坐标模型相比，具有最为简洁且便于记忆和编程的优点，故探讨中使用极坐标模型。将各参数进行复数矢量化，各个电参数变量的矢量的维数降为传统方法的 1/2，降低程序占用内存，矢量化方法可以缩短建立数学模型与开发程序的周期，代码简洁清晰，整个工程的程序比传统计算方法的程序所需要的指令数减少了 50%左右。简化雅克比的处理过程。用 MATLAB 程序实现时，在保持了程序的收敛性的情况下，修正方程数、形成雅克比用的中间变量的矩阵数减少了 1/2，处理雅克比矩阵所用的指令缩减了 1/4，提高了程序运行速度。本文所提的矢量化复数牛顿法有一个显著特性，即以复数形式的电压矢量为变量。这就意味着根据视在功率的功率平衡式，程序中是以不平衡复功率和复数的雅克比矩阵形成方式来进行潮流计算。 1本课题得到高等学校博士学科点专项科研基金（项目编号：20060593002）的资助。 -1-

中国科技论文在线 http://www.paper.edu.cn 对 4 至 1047 节点的测试系统进行大量数值仿真证明：提出方法由于它的鲁棒性和快速收敛性，为大系统的应用非常有前景。 2 极坐标下的复数潮流模型 2.1 数学准备 (1) i I R I , z ) z (2) = ⋅ ，则有 z = e ϕρ i z R 设 z z R = ⋅ ρ ϕ z I = ⋅ ρ ϕ i I + ⋅ cos ⎧ ⎨ sin ⎩ 故复变函数 R R I f z , ( ( ) ( z 1 , )ρϕ 为变量：可转换为以( f z ( ( ) ) , ρϕ 2 其中， ( ) 这样， ( ) i I + ⋅ + ⋅ = = ) 1 z f f f f 2 , ( ) ρϕ R f z 为 z 平面中区域 D 内的全纯函数， R 和 I 分别表示实部和虚部。 f z 在点 z 的导数可表示为 f ' z ( ) = f z ( lim z 0 Δ → f z ( = lim z 0 Δ → f z ( ) + Δ − z ) z Δ z ) + Δ − e i ϕ ⋅ ρ Δ ⋅ R ( ) ρ ρϕ f z ( ) + Δ , f 2 i I − ⋅ f 2 ( ) ρϕ , ρ ⋅ z R 2 f lim 0 ρ Δ → ( ) , ρϕ = − = ρ ⋅ z ( R ∂ f 2 ρ ∂ i + ⋅ I ∂ f 2 ρ ∂ ) ( ) ρ ρϕ + Δ , (3) i I + ⋅ ρ Δ f 2 z 1 1 ⋅ z 1 ⋅ ⋅ f 1 f 1 ⋅ ⋅ ⋅ ⋅ = = = = = = cos ρ ϕ cos ρ ϕ (5) (4) I ∂ z ϕ ∂ I ∂ z ∂ ϕ R ∂ z ∂ ρ R ∂ z ρ ∂ R ∂ I ∂ I ∂ f I ∂ z R ∂ f 1 cos ⋅ R ∂ z I ∂ f 1 cos ⋅ R ∂ z 同时，由(1) (2)可得 R R ∂ ∂ f 2 I ϕ ∂ ∂ I I ∂ ∂ f f 2 I ∂ ∂ ϕ z R R ∂ ∂ f f 2 R ρ ∂ ∂ z I I ∂ ∂ f f 2 R ρ ∂ ∂ z f z 满足 Cauchy-Riemann 条件，观察(4)~ (7)推出存在以下关系式：考虑到 ( ) R ∂ f 2 ϕ ∂ I ∂ f 2 ϕ ∂ (9) (8) I ∂ f 2 ρ ∂ R ∂ f 2 ρ ∂ (7) (6) ρ = − ⋅ ρ = ⋅ ϕ ϕ = = ⋅ 1 -2-

中国科技论文在线 2.2 潮流问题的复数描述 http://www.paper.edu.cn （1）不平衡复功率的计算在本次探讨中，我们考虑有 n 个节点的电力系统并采用功率方程式模型，节点电压 i ⎡ V = ⎢ 1 ⎣ i V V δ= ∠ 则采用极坐标形式。令 i i ，则矢量化的系统节点注 n∈ ， [1, ] i V n ⎤ ⎥ ⎦ ... i T i i V 入复功率为： i S = i ⋅ ) ( ∧ ∧ diag V Y V ⋅ i n ， i V R Y R × n n ∈ 式中， ∈ i i S P i Q S Δ = + ⋅ − ，由此建立矢量化的极坐标形式复数潮流方程为： (10) i ⋅ ) ∧ ∧ P i Q diag V Y V ⋅ = + ⋅ − ( i 式中，不平衡复功率 SΔ 当最大不平衡功率取不平衡复功率矩阵中各元素实部虚部绝对值的最大值时，得到与传统算法一样的收敛效果，然而这里(10)已经把每个 PQ 节点和 PV 节点的潮流方程通过复功率统一起来了。为 1n× 的复数矩阵（其详细处理方法在第三节中描述）。（2）雅克比矩阵的形成首先，将(10)式在某个近似解附近用泰勒级数展开，并略去二阶及以上的高阶项后，得到以矩阵形式的修正方程，先表示为： ) ( i J diag V ( = − ⋅ VS Δ 通常情况下，对于实变函数 ( )xf ⋅Δ i V ) − 1 (11) ，当其变量 x 为 n 维实列向量时，可认为 ( )xf nR R→ 是对n 维变量 x 的一阶导数 ( )xf∇ 的映射，即n 维变量映射出一个点。而 ( )xf 的映射，即 ( )xf∇ 为n 维列向量。然后我们观察(10)式，不平衡复功率以复数电压V 为变量，且V 是维数等于系统总节点数n 的矢量。事实上，可将复变函数分成四种类型来考虑：实变量的实函数、复变量的实函数、实变量的复函数和复变量的复函数。显然，要使用牛顿法对此潮流问题进行迭代求解，必须解决对这个复变量的复函数求偏微分的问题。，可认为是 R→ R n 由于(10)中含电压矢量的共轭，故无法直接由(3)生成雅克比矩阵。于是这里把V 看成是 i 由极坐标下的幅值和相角构成的二元函数，将 J 个由两个复数的坐标平面构成的 2 n n 数确定，分别对应 SΔ 处理为附带两个基底矢量的二阶张量，即一 × × 复数矩阵，包含 n n× 个元素，每个元素由两个复所在复平面中向量的相角和幅值梯度的牛顿迭代方向。记V V δ= ∠ S P = Δ Δ V V ( ( 这里，因为 ) ，其中V 和δ为实数，并定义 + Δ i Q * ( V ) ) (12) -3-

中国科技论文在线 http://www.paper.edu.cn ) V ) ( − Δ S ) / h ) V ( ) S V h , ) S lim( − Δ Δ V h ( , ) h 0 → S h ( lim( ⋅ Δ = ( h 0 → S ∂Δ V ∂ = 0 0 = ⋅ ， SΔ )VPΔ 和 ( 肯定满足是连续的，且 ( )VQΔ 也都是连续的。事实上，这是个由定义域上每一点都有导数的复变函数组成的全纯函数，可自由地进行微分与积分。注意到(12)式中的步长 h 可以是实数、纯虚数或复数，因此步长与V 不再是简单的相加关系，而是分别改变V 和δ。 (13) ⋅ ) = − diag V ( Q ∂Δ V ∂ P ∂Δ V ∂ 由(8)(9)可得 P ∂Δ ∂ δ Q ∂Δ ∂ δ 注意到传统牛顿法矢量化的极坐标修正方程[14]为: ⎡ ⎢ ⎣ H N M L δ Δ V V / Δ P Δ Q Δ diag V ( ⎤ ⎡ ⎥ ⎢ ⎦ ⎣ = − ⎤ ⎥ ⎦ ⎡ ⎢ ⎣ = ) ⋅ ⎤ ⎥ ⎦ (15) (14) 可见使用复导数模型得到的关系式在传统牛顿法的节点功率方程中仍然成立，但实部与虚部的计算被统一了起来。 δ ⋅ Δ + ( N i L + ⋅ ) ( ⋅ Δ V V / ) (16) ( = + ⋅ 将(15)带入(12)，得 VS H i M ) Δ ( ) 记： i i J A δ i J = ∠i J i (17) 从而由 (13) -(15)可将(16)整理成： i diag S ( ) + = i ∧ diag V diag V Y ⋅ ( ) ( ) ⋅ ∧ (18) i i diag S ( ) ( = ⋅ − i ∧ diag V diag V Y ⋅ ( ) ( ) ⋅ ∧ ) (19) i A i J i δ i J （3）复变量的更新解修正方程可得到 V e δ⋅Δ i i V Δ = Δ ⋅ 又 i V 1) + k ( δ ⋅ ( k 1) + i e ⋅ V ( δ ⋅ ( k 1) + + i e ) ⋅ k k ) V = ( V ( ( V ( i V k ( = = = k ) ⋅ V ) ⋅ Δ k ) ( ) V (1 ⋅ + Δ ( i ⋅ ( δ ( k ) +Δ δ ( k ) ) e i ⋅Δ δ ( k ) ) ⋅ e k ) V (1 ⋅ + Δ ( ) k ) ) ⋅ e i ⋅Δ δ ( k ) k -4-

中国科技论文在线 http://www.paper.edu.cn 从而可通过下式更新变量： i V (1 ⋅ + Δ + = 1) e δΔ i V ) ⋅ k k ( k ( ( ) V ( k ) ) 2.3 几何意义的讨论 i A R 由(18)(19)将修正方程(11)展开可得： R ⎡ i ⎢ δ i J ⎢ ⎢ ⎢ ⎣ δ Δ diag V ) ( 1 − ⎤ ⎥ ⎡ ⋅ ⎥ ⎢ ⎣ ⎥ ⎥ ⎦ I i δ i J ⋅ Δ ⎡ ⎢ ⎣ ⎤ ⎥ ⎦ V = P Δ Q Δ i A I i J i J i δ δ ⋅Δ + i J i A diag V ( i J ⋅ 1 − ) (1 ⋅ + Δ i S ⋅ = Δ + V i ) ⋅ Δ ⋅ = Δ ⇒ V i i S i δ δ ⇒ ⋅ Δ + i J i A diag V ( i J ⋅ − 1 ) ⎤ ⎥ ⎦ μ ，其中，因子 μ = i A diag V ( i J ⋅ − 1 ) ⋅ i i 。可见复数形式下修正方程的几何意义为：变量V 的变化方向为角度增加 δΔ ，幅值变为1 V+ Δ 倍，其变化步长分别为 i δi J 和 i A diag V ( i J ⋅ − 1 ) ⋅ i 。 3 平衡节点与 PV 节点的处理（1）不平衡复功率的处理：对于不平衡复功率矩阵的处理，我们需要将其在平衡节点对应位置上的元素整个置零；而在 PV 节点对应位置上的元素，只是将它们的虚部置零。在 4 节点算例中，处理后的不平衡复功率矩阵，形式如下所示： (0) i S Δ = (1) i S Δ = ， ⎤ ⎥ ⎥ ⎥ ⎥ ⎦ -0.2773 - 0.0513i -0.5260 + 0.0196i 0.5000 0 = ⎡ ⎢ ⎢ ⎢ ⎢ ⎣ i ⎤Δ⎢ ⎡ S ⎥ 1 ⎥ ⎢ i S Δ⎢ ⎥ 2 ⎢ ⎥ i S Δ⎢ ⎥ 3 ⎥ ⎢ i S ⎢ ⎥Δ⎣ ⎦ -0.0000 - 0.0438i ⎡ ⎢ -0.0205 - 0.0245i ⎢ ⎢ ⎢ ⎣ 0.0045 0 4 ， ⎤ ⎥ ⎥ ⎥ ⎥ ⎦ (2) i S Δ = 1.0e-003 * 0.0996 - 0.4506i -0.4200 - 0.3182i 0.0795 0 ⎡ ⎢ ⎢ ⎢ ⎢ ⎣ 。 ⎤ ⎥ ⎥ ⎥ ⎥ ⎦ （2）雅克比矩阵的处理： ①平衡节点的处理：比较(18)(19)式，事实上， i δi J 、 i Ai J 都是由 i diag S ( ) 项和 -5- i ∧ diag V diag V Y ⋅ ( ) ( ) ⋅ ∧ 项计算得

中国科技论文在线 http://www.paper.edu.cn 到的。而 i diag S ( ) 是对角阵，故对平衡节点的处理只需将 i ∧ diag V diag V Y ⋅ ( ) ( ) ⋅ ∧ 项计算得到的 n n× 复数矩阵在平衡节点对应的行和列上所有的元素置零，则得到的 i δi J 、 i Ai J 即为在平衡节点对应的行和列上所有的元素为零的n n× 复数矩阵。 ②PV 节点的处理：将 i Ai J 在 PV 节点对应的列上的所有元素置零，对应的行上所有元素的虚部置零；将 i δi J 在 PV 节点对应的行上所有元素的虚部置零。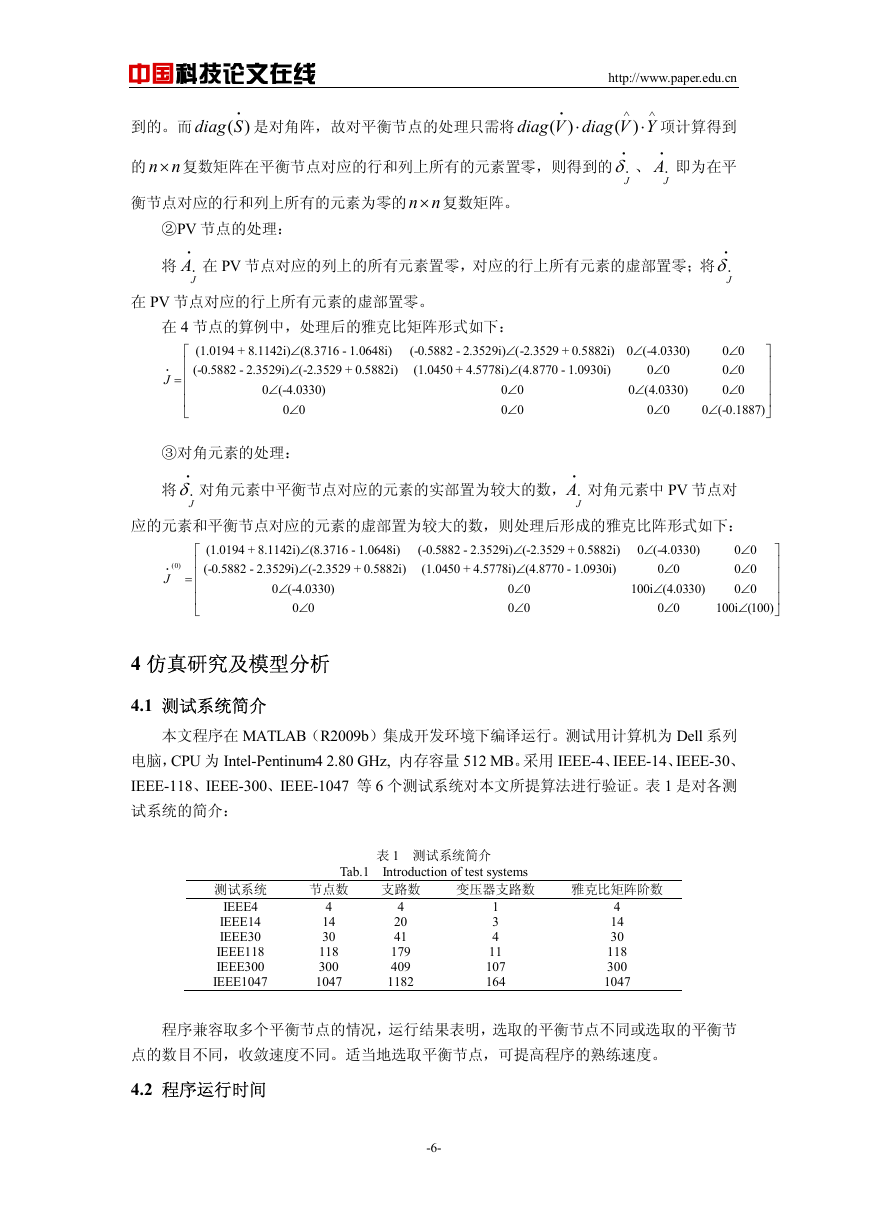 (8.3716 - 1.0648i) (1.0194 + 8.1142i) ∠ (-2.3529 + 0.5882i) (-0.5882 - 2.3529i) ∠ 在 4 节点的算例中，处理后的雅克比矩阵形式如下： (-2.3529 + 0.5882i) 0 (-4.0330) (-0.5882 - 2.3529i) ∠ (1.0450 + 4.5778i) (4.8770 - 1.0930i) ∠ 0 0 ∠ 0 0 ∠ 0 (-4.0330) ∠ 0 (4.0330) ∠ 0 0 ∠ 0 0 ∠ 0 0 ∠ ∠ i J = ⎡ ⎢ ⎢ ⎢ ⎢ ⎣ 0 0 ∠ 0 0 ∠ 0 0 ∠ 0 (-0.1887) ∠ ⎤ ⎥ ⎥ ⎥ ⎥ ⎦ ③对角元素的处理：将 i δi J 对角元素中平衡节点对应的元素的实部置为较大的数， i Ai J 对角元素中 PV 节点对应的元素和平衡节点对应的元素的虚部置为较大的数，则处理后形成的雅克比阵形式如下： 0 0 ∠ 0 0 ∠ 0 0 ∠ (100) ∠ (-2.3529 + 0.5882i) (-0.5882 - 2.3529i) ∠ (1.0450 + 4.5778i) (4.8770 - 1.0930i) ∠ 0 0 ∠ 0 0 ∠ (8.3716 - 1.0648i) (1.0194 + 8.1142i) ∠ (-2.3529 + 0.5882i) (-0.5882 - 2.3529i) ∠ 0 0 ∠ (4 ∠ 0 0 ∠ 0 (-4.0330) ∠ 0 (-4.0330) ∠ .0330) 100i 100i 0 0 ∠ i J = (0) ⎡ ⎢ ⎢ ⎢ ⎢ ⎣ 4 仿真研究及模型分析 ⎤ ⎥ ⎥ ⎥ ⎥ ⎦ 4.1 测试系统简介本文程序在 MATLAB（R2009b）集成开发环境下编译运行。测试用计算机为 Dell 系列电脑，CPU 为 Intel-Pentinum4 2.80 GHz, 内存容量 512 MB。采用 IEEE-4、IEEE-14、IEEE-30、 IEEE-118、IEEE-300、IEEE-1047 等 6 个测试系统对本文所提算法进行验证。表 1 是对各测试系统的简介：测试系统 IEEE4 IEEE14 IEEE30 IEEE118 IEEE300 IEEE1047 表 1 测试系统简介 Tab.1 Introduction of test systems 变压器支路数支路数节点数 4 14 30 118 300 1047 4 20 41 179 409 1182 1 3 4 11 107 164 雅克比矩阵阶数 4 14 30 118 300 1047 程序兼容取多个平衡节点的情况，运行结果表明，选取的平衡节点不同或选取的平衡节点的数目不同，收敛速度不同。适当地选取平衡节点，可提高程序的熟练速度。 4.2 程序运行时间 -6-

中国科技论文在线 http://www.paper.edu.cn 使用矢量化的方法能充分利用计算机的分级存储体系，针对高速缓存器的连续数据进行运算；保证施加在高速缓存器中的计算与存储单元中的数据地址无关，减少取指令时间和计算操作数地址的时间，提高 CPU 对核心计算任务的执行效率。这样不仅计算速度更快，整个程序的性能也得到提升。各计算模块运行时间如表 2 所示：测试系统 IEEE4 IEEE14 IEEE30 IEEE118 IEEE300 IEEE1047 0. 251 0.300 0.339 0.602 1.097 2.860 Sline(ms) 0. 096 0. 111 0. 130 0. 249 0. 421 1.037 表 2 程序运行时间和迭代次数 Tab.2 CPU time and iterations 形成 Y(ms) 计算耗时(ms) 迭代次数/精度 1.448 1.990 4.058 9.743 31.281 104.451 2/1.e-3 2/1.e-3 3/1.e-5 3/1.e-5 4/1.e-3 4/1.e-5 表 2 列出了各测试系统在变压器模型取第四种模型下的程序的运行时间和迭代次数。程序的迭代速度与平衡节点的选取方式有直接联系，但迭代次数基本不变，故表 2 的参数展示了典型的选取一个平衡节点时的计算情况。模块功能求不平衡量形成雅克比矩阵解修正方程表 3 IEEE1047 系统潮流计算数据 Tab.3 PF calculation statistics of IEEE1047 system 指令数调用内置函数数耗时(s) 0.006 0.046 0.073 6 8 2 5 4 4 CPU 使用峰值 40% 从表 3 可以看出，形成雅克比矩阵和解修正方程两个模块的程序非常简洁。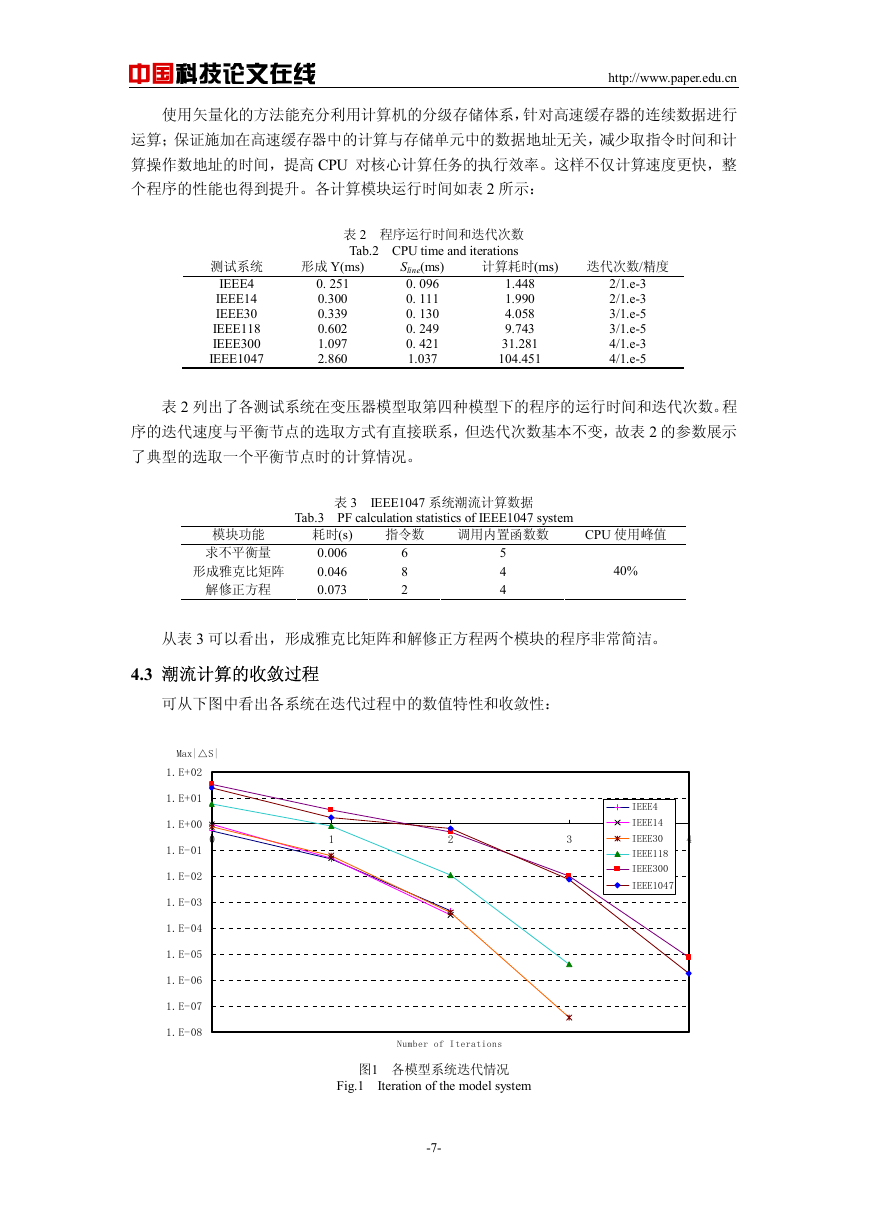 4.3 潮流计算的收敛过程可从下图中看出各系统在迭代过程中的数值特性和收敛性： Max|△S| 1.E+02 1.E+01 1.E+00 1.E-01 1.E-02 1.E-03 1.E-04 1.E-05 1.E-06 1.E-07 1.E-08 0 1 2 3 IEEE4 IEEE14 IEEE30 IEEE118 IEEE300 IEEE1047 4 Number of Iterations 图1 各模型系统迭代情况 Fig.1 Iteration of the model system -7-

中国科技论文在线 http://www.paper.edu.cn 可以看到，本文模型及算法仍可以有效迭代收敛，复数矢量化的方法形成雅克比矩阵时体现出其高效的利用内存空间能力，其计算结果与未使用的程序的运行结果完全一致，但计算所需的资源规模大为减少，系统越大，效果越明显。 5 结语本文提出了一种矢量化复数牛顿法来求解潮流问题，不仅简化了程序代码，而且由于缩小了变量的大小，故大大节省了运算过程中占用的存储空间。程序在 MATLAB（R2009b）环境下实现的运行结果表明，这种采用稀疏技术进行基于矢量化与复数矩阵运算方式的编程，不仅程序代码简洁高效，而且计算速度高，代码具有良好的通用性和易维护性，可用于大规模系统。参考文献 [1] S. M. Hetzler. A Continuous Version of Newton’s Method [J]．College Math. J, 1997, 28( 5): 348-351． [2] R. van Amerongen．A General-purpose Version of the Fast Decoupled Loadflow [J]．IEEE Trans. Power Syst. , 1989, 4(2): 760-770． [3] S. Iwamoto, Y. Tamura．A Load Flow Calculation Method for Ill-conditioned Power Systems [J]．IEEE Trans. Power App. Syst., 1981, vol. PAS- 100: 1736-1743． [4] S. Iwamoto, Y. Tamura．A Fast Load Flow Method Retaining nonlinearity [J]．IEEE Trans. Power App. Syst., 1978, vol. PAS-97: 1586-1599． Appl.,1988, 24: 870-877． [5] M. D. Schaffer, D. J. Tylavsky．A Nondiverging Polar-form Newton-based Power flow [J]．IEEE Trans. Ind. [6] D. J. Tylavsky, P. Crouch, L. F. Jarriel, et al．Improved Power Flow Robustness for Personal Computers [J]．IEEE Trans. Ind. Appl., 1992, 28: 1102-1108． [7] L. M. C. Braz, C. A. Castro, C. A. F. Murari．A Critical Evaluation of Step Size Optimization Based Load Flow Methods [J]．IEEE Trans. Power Syst., 2000, 15(1): 202-207． [8] P. R. Bijwe, S. M. Kelapure．Nondivergent Fast Power Flow Methods [J]．IEEE Trans. Power Syst., 2003, 18( 2): 633-638． 24(1): 50-57． [9] J. E. Tate, T. J. Overbye．A Comparison of the Optimal Multiplier in Polar and Rectangular Coordinates [J]．IEEE Trans. Power Syst., 2005, 20(4): 1667-1674． [10] Federico Milano．Continuous Newton’s Method for Power Flow Analysis [J]．IEEE Trans. Power Syst., 2009, [11] 诸骏伟．《电力系统分析 (上) 》[M]．北京：水利电力出版社，1995． [12] 何仰赞，温增银．《电力系统分析》[M]．武汉：华中科技大学出版社，2002． [13] J.Duncan Glover ．《 Mulukutla S.Sarma. Power System Analysis and Design 》 [M] ． CA, USA: BROOKS/COLE, 2001． [14] 苏津，阳育德，覃智君．基于矢量化运算模式的电力系统潮流计算 [J]．电网技术, 2008, 32(3): 88-92． [15] Su Jin, Yang Yude, Qin Zhijun．Power flow calculation based on vectorized operation mode [J]．Power System Technology, 2008, 32(3): 88-92． -8-

分享到：

赞收藏

资料库

一种解潮流问题的矢量化复数牛顿法.pdf

相关推荐

开发技术

热门标签

最新资料