logo资料库

一种基于高斯混合模型的轨迹预测算法_乔少杰.pdf

发布时间：2022-06-01 发布人：admin 分类：说明书 资料大小：1.01M 资料格式：pdf 举报 版权申诉
第1页 / 共16页
第2页 / 共16页
第3页 / 共16页
第4页 / 共16页
第5页 / 共16页
第6页 / 共16页
第7页 / 共16页
第8页 / 共16页
资料共16页，剩余部分请下载后查看
    软件学报 ISSN 1000-9825, CODEN RUXUEW Journal of Software,2015,26(5):10481063 [doi: 10.13328/j.cnki.jos.004796] ©中国科学院软件研究所版权所有. E-mail: jos@iscas.ac.cn http://www.jos.org.cn Tel: +86-10-62562563 一种基于高斯混合模型的轨迹预测算法 乔少杰 1, 金 琨 1, 韩 楠 2, 唐常杰 3, 格桑多吉 4, Louis Alberto GUTIERREZ5   1(西南交通大学 信息科学与技术学院,四川 成都 610031) 2(西南交通大学 生命科学与工程学院,四川 成都 610031) 3(四川大学 计算机学院,四川 成都 610065) 4(西藏大学 藏文信息技术研究中心,西藏 拉萨 850000) 5(Department of Computer Science, Rensselaer Polytechnic Institute, New York, USA) 通讯作者: 韩楠, E-mail: hannan@swjtu.edu.cn 摘 要: 在智能交通控制系统、军事数字化战场、辅助驾驶系统中,实时、精确、可靠的移动对象不确定性轨迹 预测具有极高的应用价值.智能轨迹预测不仅可以提供精准的基于位置的服务,而且可以提前监测和预判交通状况, 进而推荐最佳路线,已经成为移动对象数据库研究的热点,亟需设计准确而高效的位置预测方法.针对现有方法的不 足,提出了基于高斯混合模型的轨迹预测方法 GMTP,主要步骤包括:(1) 针对复杂运动模式利用高斯混合模型建 模;(2) 利用高斯混合模型计算不同运动模式的概率分布,进而将轨迹数据划分为不同分量;(3) 利用高斯过程回归 预测移动对象最可能的运动轨迹.GMTP 是高斯非线性概率统计模型,其优势在于:计算结果不仅是位置预测值,更 是关于移动对象未来所有可能运动轨迹的概率分布,可以利用概率统计分布特性获得某种运动模式(如匀加速运 动)下的位置预测.大量真实轨迹数据集上的实验结果表明:与相同参数设置下的高斯回归预测和卡尔曼滤波预测 法相比,GMTP 的预测准确性平均提高了 22.2%和 23.8%,预测时间平均缩减了 92.7%和 95.9%. 关键词: 移动对象数据库;轨迹预测;高斯混合模型;运动模式 中图法分类号: TP18 中文引用格式: 乔少杰,金琨,韩楠,唐常杰,格桑多吉,Gutierrez LA.一种基于高斯混合模型的轨迹预测算法.软件学报,2015, 26(5):10481063. http://www.jos.org.cn/1000-9825/4796.htm 英文引用格式: Qiao SJ, Jin K, Han N, Tang CJ, Gesangduoji, Gutierrez LA. Trajectory prediction algorithm based on Gaussian mixture model. Ruan Jian Xue Bao/Journal of Software, 2015,26(5):10481063 (in Chinese). http://www.jos.org.cn/1000-9825/ 4796.htm Trajectory Prediction Algorithm Based on Gaussian Mixture Model QIAO Shao-Jie1, JIN Kun1, HAN Nan2, TANG Chang-Jie3, Gesangduoji4, Louis Alberto GUTIERREZ5 1(School of Information Science and Technology, Southwest Jiaotong University, Chengdu 610031, China) 2(School of Life Science and Engineering, Southwest Jiaotong University, Chengdu 610031, China) 3(College of Computer Science, Sichuan University, Chengdu 610065, China) 4(Tibetan Information Technology Research Center, Tibet University, Lasa 850000, China) 5(Department of Computer Science, Rensselaer Polytechnic Institute, New York, USA)  基金项目: 国家自然科学基金(61100045, 61165013); 教育部高等学校博士学科点专项科研基金(20110184120008); 教育部人 文社会科学研究青年基金(14YJCZH046); 中央高校基本科研业务费专项资金(2682013BR023); 科学计算与智能信息处理广西高校 重点实验室开放课题(GXSCIIP201407) 收稿时间: 2014-07-10; 修改时间: 2014-09-29; 定稿时间: 2014-11-25; jos 在线出版时间: 2015-02-02 CNKI 网络优先出版: 2015-02-02 15:24, http://www.cnki.net/kcms/detail/11.2560.TP.20150202.1524.005.html
    乔少杰 等:一种基于高斯混合模型的轨迹预测算法 1049 Abstract: For intelligent transportation systems, digital military battlefield and driver assistance systems, it is of great practical value to predict the trajectories of moving objects with uncertainty in a real-time, accurate and reliable fashion. Intelligent trajectory prediction can not only provide accurate location-based services, but also monitor and estimate traffic to suggest the best path, and as such becomes an active research direction. Aiming to overcome the drawbacks of the existing methods, a new trajectory prediction model based on Gaussian mixture models called GMTP is proposed. The new model contains the following essential phases: (1) modeling the complex motion patterns based on Gaussian mixture models, (2) calculating the probability distribution of different types of motion patterns by using Gaussian mixture model in order to partition trajectory data into distinct components, and (3) inferring the most possible trajectories of moving objects via Gaussian process regression. The GMTP algorithm is naturally a Gaussian nonlinear statistical probability model and the advantage of the proposed model is that the result is not only a predicted value, but also a whole distribution beyond the future trajectories, therefore making it possible to infer the location in regard to some motion patterns, e.g., uniformly accelerated motion, by using statistical probability distribution. Extensive experiments are conducted on real trajectory data sets and the results show that the prediction accuracy of the GMTP algorithm is improved by 22.2% and 23.8%, and the runtime can be reduced by 92.7% and 95.9% on average, respectively, when compared to the Gaussian process regression model and Kalman filter prediction algorithm with similar parameter setting. Key words: moving objects database; trajectory prediction; Gaussian mixture model; motion pattern 随着无线移动通信设备和无线车载传感器的发展,获取移动对象时空位置的手段更加多样化.在诸多重要 应用领域中,如智能交通系统(ITS)、智能导航、数字化战场、物流配送、移动电子商务等,用户都需要及时查 询和分析各种移动对象的轨迹位置信息,移动对象轨迹位置预测已经逐渐成为移动对象数据管理[1]中极为重 要的研究方向.当前,数字化城市的公共交通车辆、出租车以及其他一些车辆都配备 GPS 及车载导航设备,可以 将不同时刻采集到的车辆位置信息连接起来,构成完整的轨迹时间序列,进而挖掘其动态运动模式.对移动对象 的轨迹信息挖掘的目的在于:在短时间内,可以提醒处于拥堵十字路口的驾驶员车辆前行的安全性;在长时间 内,预测可能会发生交通堵塞的区域,及时做出调度,引导交通并提醒驾驶员及时做出路线调整.在一般情况下, 移动对象总是周期性地向中央服务器发送其位置信息,然而在两次定位信息传递时间内,移动对象的具体位置 信息和运动轨迹是无从得知的.此外,移动对象运动环境的多样化也使问题更加复杂.如何对移动对象位置信息 准确预测,成为亟需解决的难点.当前已有一些研究成果,如移动对象的聚类、异常检测以及定位和运动趋势的 预测.其中,对移动对象位置预测技术不断地完善,但由于理论和技术的不成熟,大多数模型不能很好地适应不 断发展的移动计算技术的需要.诸如单一线性回归预测、神经网络预测、Markov 模型位置预测[2,3]等传统方法, 因其理论的局限性,未能应用于对实时性、抗干扰性要求较高的移动通信环境中. 1 相关工作 移动对象按照空间分布特性被分为 3 类:(1) 运动道路不受限制,如飞机、轮船、带有传感器的鸽子等;(2) 运 动轨道受限制,如公路行驶的车辆;(3) 运动道路轨迹分散,如移动用户.针对移动对象的位置预测主要分为过去 轨迹的重现、当前和未来轨迹的预测.本文主要研究对象是运动道路轨迹分散的移动对象,同时解决该类移动 对象的未来轨迹预测问题.当前,轨迹预测方法主要集中于轨迹频繁模式挖掘,通过挖掘频繁模式找出典型运动 模式[4].代表性工作由 Morzy 等人[5]提出,提出一种结合前缀树 PrefixSpan 和频繁模式挖掘 FP-tree 算法挖掘移 动对象动态运动规则,但是构建前缀树和 FP-tree 的时间代价较高.Jeung 等人[6]提出了一种综合考虑移动对象运 动模式和运动函数的混合预测方法,然而提供的查询预测仅支持短期的查询结果.大多数轨迹预测方法基于轨 迹的地理特性,而 Ying 等人[7]结合个体运动轨迹的语义特征和空间位置预测移动对象下一位置信息.这一方法 的不足在于计算每条候选路径的 Semantic Score 时,代价较高.Zheng 等人[8]考虑个体的旅行经历和兴趣爱好, 提出了一种 Hypertext Induced Topic Search 模型推测其感兴趣的运动路线,但这一方法主要应用于向用户推荐 可能感兴趣的地点,不能给出一整条完整的运动曲线.本文的研究动机源于 Song 等人[9]在 Science 上发表的介绍 预测人类移动性的工作,通过测量个体轨迹的信息熵,定量地给出了人类动态运动行为,具有 93%的可预测性.围 绕这一工作,近期,Pan 等人[10]提出了基于多变元正态分布的最佳线性预测器,这一方法的不足在于预测会产生
    1050 Journal of Software 软件学报 Vol.26, No.5, May 2015 延迟,不能应用于交通流的实时监控.Zhou 等人[11]提出了一种称为“semi-lazy”的预测方法,利用动态选取的参考 轨迹构建预测模型,优点是可以基于少量的参考轨迹构建精准的模型.近期,针对受限路网中轨迹预测精度不高 的问题,Qiao 等人[3]提出了一种基于隐马尔卡夫模型的轨迹预测算法 HMTP,从海量轨迹数据中提取隐状态和 观察状态,根据不同类型的轨迹,自适应地预测最佳轨迹.与本文的工作不同点在于:本文提出了一种通用的轨 迹预测算法,不仅仅适用于受限路网中移动对象的轨迹预测问题. 大多数轨迹预测问题针对的都是受限路网中移动对象的位置查询和预测[12].Tao 等人[13]提出一种基于未 知模型的预测方法,弥补了线性预测的缺陷,将轨迹数据存储在 TPR*树中,使用递归函数进行预测.然而,这一方 法忽略了主、客观不确定性因素的影响.Qiao 等人[14]充分考虑了影响移动对象位置变化的运动速度、方向和 路况信息,设计了一种基于时间连续贝叶斯网络的连续轨迹序列预测算法.实验证明,这一方法在轨迹预测的准 确性和时效性上均优于朴素预测算法.为了进一步提高预测结果的准确性和时效性,文献[12]提出了一种基于 轨迹时间连续贝叶斯网络的轨迹预测算法 TPMO,考虑了移动速度和方向对移动对象动态运动行为的影响.与 本文工作的不同点在于:本文所提出的预测算法可以解决轨迹离散状态预测准确性较差的问题,并且对于移动 对象轨迹的预测,可以依据概率模型精确度量其预测误差. 从时空轨迹数据中挖掘运动模式的多样性,对移动对象位置预测也是至关重要的.轨迹运动模式建模需要 对状态空间进行离散化分析,Hu 等人[15]将轨迹模型视为离散状态点之间转变的过渡,离散状态分析方法的不足 在于:需要对大量时空数据进行离散化处理,并且需要分析离散数据点之间的关联.Feng 等人[16]基于隐马尔可 夫模型重现移动对象轨迹序列,这一方法无需考虑对象缺失的观察状态信息,但是预测准确率不高.Gaffney 和 Smyth 提出对原始连续轨迹基于原型的聚类方法[17],通过增加高斯噪声,将具有相似轨迹部分的移动对象聚合 在一起,使用最大似然原理实现无监督学习.这是一种比较新颖和实用的轨迹数据分析方法,在本文的后续工作 中,借鉴其利用 EM 算法来确定轨迹聚类的簇个数,并考虑了聚类簇中轨迹点离散空间和时间偏移.轨迹位置预 测中,稳定线性回归如卡尔曼滤波对短时间内(1 步或 2 步)的预测有比较稳定准确的判断[18],而对于长时间(未 来 5 步以上)的预测,仅当处理的轨迹数据是无噪声点的情况才比较有效.高斯过程回归方法对于处理具有噪声 点的数据有着比较好的预测效果,是一种基于非参数的概率性方法,而且所使用的训练数据集规模比较小[19]. Qiao 等人[20]对轨迹数据构建双层索引,利用 RoI(region-of-interest)检查算法对轨迹进行划分,构建频繁轨迹模 式树预测移动对象最可能运动模式.针对上述研究的不足,本文提出了基于高斯混合模型(Gaussian mixture model,简称 GMM)的轨迹建模方法,利用概率模型刻画运动轨迹.其优势在于:可以摆脱轨迹离散状态分析方法 的弊端,并且对于移动对象轨迹的预测,可以依据概率模型精确度量其预测误差. 2 基本概念及模型框架 本节首先给出几个主要概念,然后介绍本文所提出模型的框架及工作原理. 已知移动对象数据库 D,其中存储大量运动对象在不同时间采样点的位置信息,位置点在时间上的有序集 合称为轨迹,用 D={Trj1,Trj2,...,Trjn}表示,轨迹的数量定义为|D|.本文对轨迹作如下定义: 定义 1(轨迹序列). 移动对象原始轨迹序列 Trj={s1,s2,...,sd}表示有序的离散轨迹点{si=(xi,yi,ti)|1≤i≤d}所 构成的序列,其中,ti 表示时间戳,i[1,d),ti
    乔少杰 等:一种基于高斯混合模型的轨迹预测算法 和协方差函数 k(x,x)确定,即 其中,m(x)=E[f(x)],k(x,x)=E[(f(x)m(x))(f(x)m(x))].本文采用的核函数为标准指数协方差函数,即 f(x)~GP(m(x),k(x,x)) Cov f x f x )) (  ( ), (  2 k x x  ( , 0 )   exp    ( x  2 x )  2 2  1     2  ij 1051 (1) (2) 其中,0 为指数权重,θ1 表示长度规模,ij 是狄拉克函数.当 i=j 时,函数ij=1,否则为 0. 定义 4(轨迹高斯混合模型). 轨迹高斯混合模型中,每个状态用一个高斯过程函数表示,即,数据是由多个高 斯过程模型线性组合产生的,用公式(3)、公式(4)来表示轨迹点在二维坐标系下的 GMM 模型.假设数据点(x,y) 是多维运动矢量,其随机生成来自 M 个相互独立的高斯过程线性组合的总体 G={GP1,GP2,...,GPM},且每个高斯 过程对应的权重分为为1,2,...,M,混合而成的总体分布为 G,于是,x 的概率密度函数为 GP x ( p x ( )  (3) ) | |   j j ,     M  j j 1  M  j j 1  (4)  M j  j 1  1. 表 p y ( | )  GP y ( |   i i , ) 其中,GP()表示高斯过程的概率密度函数,M 表示高斯过程数量,j 为第 j 个高斯过程的权重,且 示此密度函数中心点,表示协方差矩阵.参数用集合表示为={i,i,i},i=1,…,M. 定义 5(预测误差). 轨迹预测时,将测试轨迹数据集输入预测模型得到预测输出轨迹,其中,输入测试轨迹为 部分轨迹点的集合,预测输出点由图 1 中虚线表示. 预测轨迹路线 ( x y , 2  2 ) ( x y ,  1 1 ) (x3,y3) ( x y ,  3 3 ) (x2,y2) (x1,y1) 实际轨迹路线 Y v v 输入历史轨迹点 X Fig.1 An example of predicted trajectories 图 1 预测轨迹示例 采用公式(5)所示的均方根误差 RMSE 来计算预测轨迹点与实际轨迹点的几何空间误差: RMSE  k  i 1  ( x  i  x i 2 )  ( y  i  y i 2 ) k 其中,(xi,yi)表示真实位置, (  表示预测位置,k 为预测轨迹点的数量. 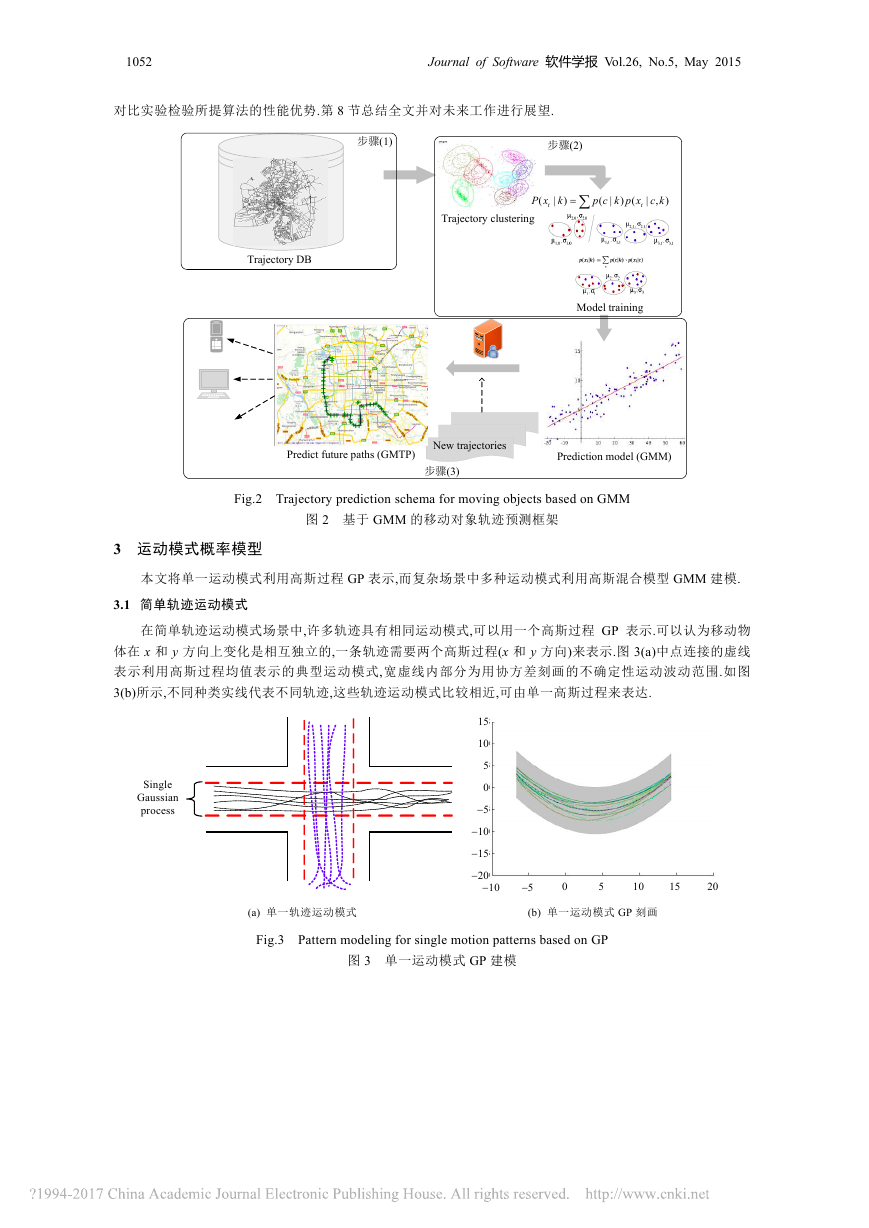x y ) , i i (5) 本文所提出模型的系统框架如图 2 所示,其工作原理分为 3 个步骤: (1) 利用 ETL 技术将历史轨迹预处理后转化为轨迹矢量存储于数据库中; (2) 对不同运动模式轨迹数据进行 GMM 聚类分析,利用最大似然估计 EM 算法求得聚类模型参数,使其 基于历史数据模型概率达到最大化,获得 M个聚簇; (3) 利用最小二乘法和高斯混合回归模型训练得到预测模型 GMTP,根据输入的新轨迹数据预测移动对 象未来最可能的运动轨迹. 本文第 3 节形式化给出移动对象简单和复杂轨迹运动概率模型.第 4 节给出高斯混合模型回归预测理论基 础.第 5 节详细阐述 GMM 轨迹预测模型训练和学习原理.第 6 节介绍基于 GMM 的轨迹预测算法.第 7 节通过
    1052 Journal of Software 软件学报 Vol.26, No.5, May 2015 对比实验检验所提算法的性能优势.第 8 节总结全文并对未来工作进行展望. 步骤(2) P x k ( | t )   p c k p x c k ( , ) ) ( | | t Trajectory clustering 步骤(1) Trajectory DB Predict future paths (GMTP) New trajectories 步骤(3) Model training Prediction model (GMM) Fig.2 Trajectory prediction schema for moving objects based on GMM 图 2 基于 GMM 的移动对象轨迹预测框架 3 运动模式概率模型 本文将单一运动模式利用高斯过程 GP 表示,而复杂场景中多种运动模式利用高斯混合模型 GMM 建模. 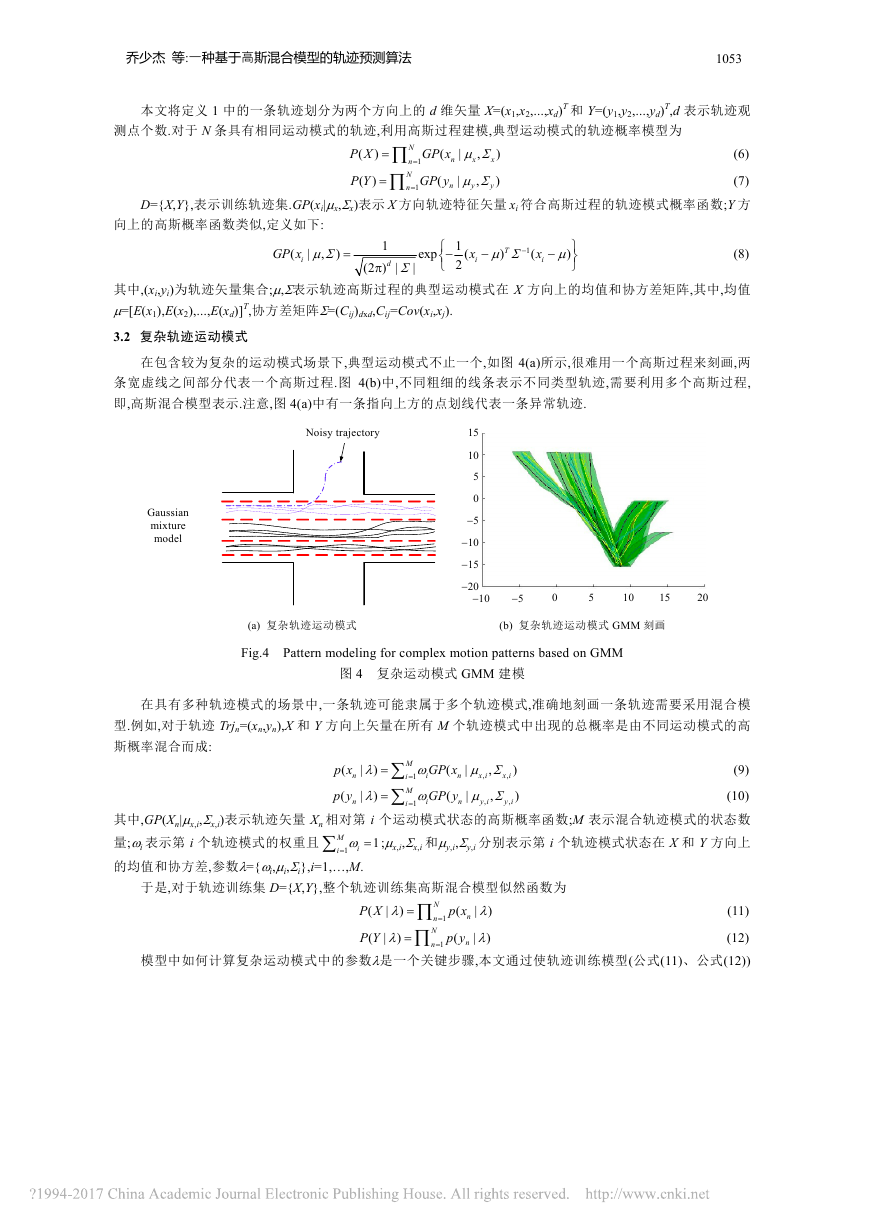3.1 简单轨迹运动模式 在简单轨迹运动模式场景中,许多轨迹具有相同运动模式,可以用一个高斯过程 GP 表示.可以认为移动物 体在 x 和 y 方向上变化是相互独立的,一条轨迹需要两个高斯过程(x 和 y 方向)来表示.图 3(a)中点连接的虚线 表示利用高斯过程均值表示的典型运动模式,宽虚线内部分为用协方差刻画的不确定性运动波动范围.如图 3(b)所示,不同种类实线代表不同轨迹,这些轨迹运动模式比较相近,可由单一高斯过程来表达. Single Gaussian process 15 10 5 0 5 10 15 20 10 5 0 5 10 15 20 (a) 单一轨迹运动模式 (b) 单一运动模式 GP 刻画 Fig.3 Pattern modeling for single motion patterns based on GP 图 3 单一运动模式 GP 建模
    P X ( P Y ( )     n | , ( N GP x   x n 1  N GP y   y n 1  x 乔少杰 等:一种基于高斯混合模型的轨迹预测算法 1053 本文将定义 1 中的一条轨迹划分为两个方向上的 d 维矢量 X=(x1,x2,...,xd)T 和 Y=(y1,y2,...,yd)T,d 表示轨迹观 测点个数.对于 N 条具有相同运动模式的轨迹,利用高斯过程建模,典型运动模式的轨迹概率模型为 ) ) (6) (7) D={X,Y},表示训练轨迹集.GP(xi|x,x)表示 X 方向轨迹特征矢量 xi 符合高斯过程的轨迹模式概率函数;Y 方 ( ) , | n y 向上的高斯概率函数类似,定义如下: GP x ( i | )  ,  1 d (2 )  exp     1 2 |  | ( x i  1    T ) ( x i  )     (8) 其中,(xi,yi)为轨迹矢量集合;,表示轨迹高斯过程的典型运动模式在 X 方向上的均值和协方差矩阵,其中,均值 =[E(x1),E(x2),...,E(xd)]T,协方差矩阵=(Cij)dxd,Cij=Cov(xi,xj). 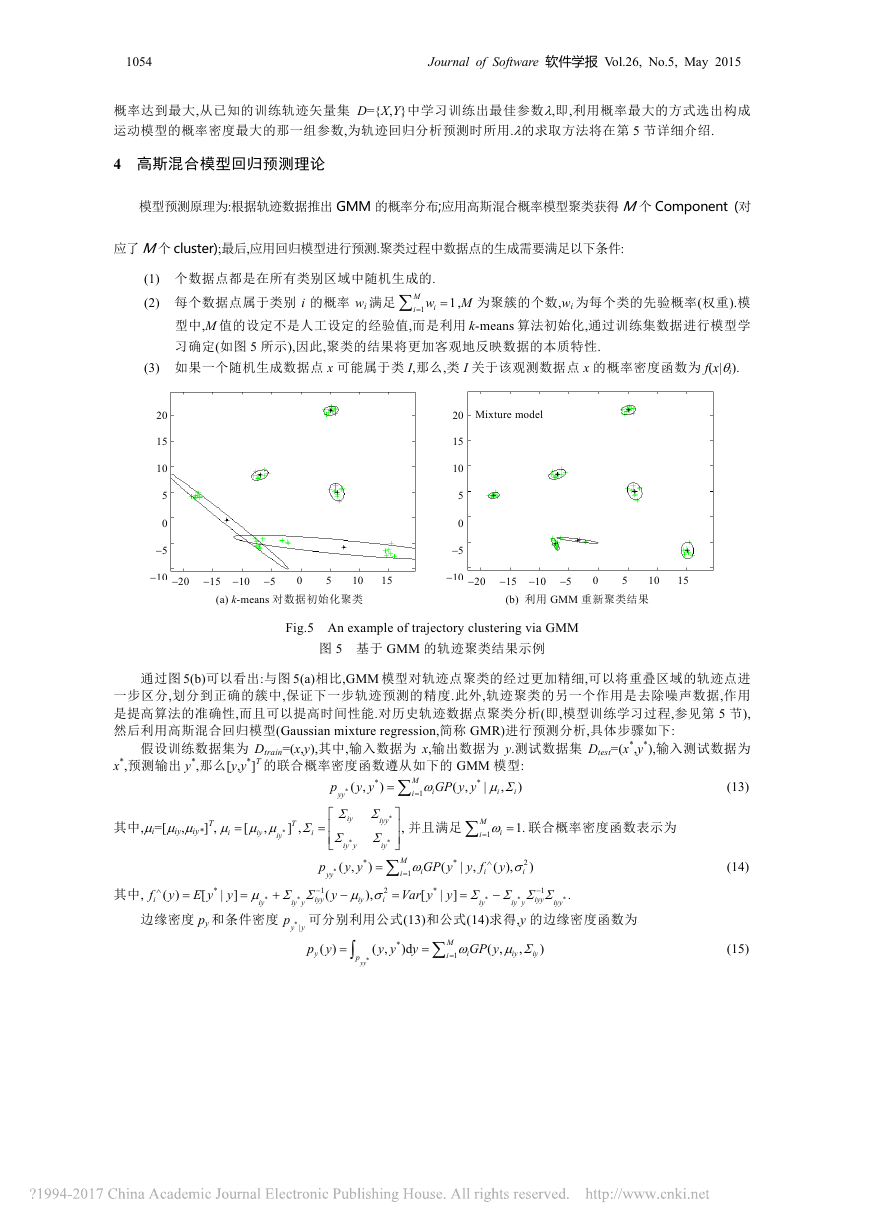3.2 复杂轨迹运动模式 在包含较为复杂的运动模式场景下,典型运动模式不止一个,如图 4(a)所示,很难用一个高斯过程来刻画,两 条宽虚线之间部分代表一个高斯过程.图 4(b)中,不同粗细的线条表示不同类型轨迹,需要利用多个高斯过程, 即,高斯混合模型表示.注意,图 4(a)中有一条指向上方的点划线代表一条异常轨迹. Gaussian mixture model Noisy trajectory 15 10 5 0 5 10 15 20 10 5 0 5 10 15 20 (a) 复杂轨迹运动模式 (b) 复杂轨迹运动模式 GMM 刻画 Fig.4 Pattern modeling for complex motion patterns based on GMM 图 4 复杂运动模式 GMM 建模 在具有多种轨迹模式的场景中,一条轨迹可能隶属于多个轨迹模式,准确地刻画一条轨迹需要采用混合模 型.例如,对于轨迹 Trjn=(xn,yn),X 和 Y 方向上矢量在所有 M 个轨迹模式中出现的总概率是由不同运动模式的高 斯概率混合而成: )  (9) ) , | | (10) 其中,GP(Xn|x,i,x,i)表示轨迹矢量 Xn 相对第 i 个运动模式状态的高斯概率函数;M 表示混合轨迹模式的状态数 M 量;i 表示第 i 个轨迹模式的权重且 1 ;x,i,x,i 和y,i,y,i 分别表示第 i 个轨迹模式状态在 X 和 Y 方向上  i  i 的均值和协方差,参数={i,i,i},i=1,…,M.  )  1 ) | | n n 于是,对于轨迹训练集 D={X,Y},整个轨迹训练集高斯混合模型似然函数为 p x ( n p y (     M  i i 1  M  i i 1  GP x ( n GP y ( x i ,   x i ,   y i , y i , , (12) 模型中如何计算复杂运动模式中的参数是一个关键步骤,本文通过使轨迹训练模型(公式(11)、公式(12)) )  )  | | n P X ( P Y ( | )      N n 1  N n 1  p x ( n p y ( | )  (11)
    1054 Journal of Software 软件学报 Vol.26, No.5, May 2015 概率达到最大,从已知的训练轨迹矢量集 D={X,Y}中学习训练出最佳参数,即,利用概率最大的方式选出构成 运动模型的概率密度最大的那一组参数,为轨迹回归分析预测时所用.的求取方法将在第 5 节详细介绍. 4 高斯混合模型回归预测理论 模型预测原理为:根据轨迹数据推出 GMM 的概率分布;应用高斯混合概率模型聚类获得 M个 Component (对 应了M个 cluster);最后,应用回归模型进行预测.聚类过程中数据点的生成需要满足以下条件: (1) 个数据点都是在所有类别区域中随机生成的. (2) 每个数据点属于类别 i 的概率 wi 满足 1 i w  M ,M 为聚簇的个数,wi 为每个类的先验概率(权重).模 型中,M 值的设定不是人工设定的经验值,而是利用 k-means 算法初始化,通过训练集数据进行模型学 习确定(如图 5 所示),因此,聚类的结果将更加客观地反映数据的本质特性.  1 i (3) 如果一个随机生成数据点 x 可能属于类 I,那么,类 I 关于该观测数据点 x 的概率密度函数为 f(x|i). 20 15 10 5 0 5 10 20 15 10 5 0 5 10 15 Mixture model 20 15 10 5 0 5 10 20 15 10 5 0 5 10 15 (a) k-means 对数据初始化聚类 (b) 利用 GMM 重新聚类结果 Fig.5 An example of trajectory clustering via GMM 图 5 基于 GMM 的轨迹聚类结果示例 通过图 5(b)可以看出:与图 5(a)相比,GMM 模型对轨迹点聚类的经过更加精细,可以将重叠区域的轨迹点进 一步区分,划分到正确的簇中,保证下一步轨迹预测的精度.此外,轨迹聚类的另一个作用是去除噪声数据,作用 是提高算法的准确性,而且可以提高时间性能.对历史轨迹数据点聚类分析(即,模型训练学习过程,参见第 5 节), 然后利用高斯混合回归模型(Gaussian mixture regression,简称 GMR)进行预测分析,具体步骤如下: 假设训练数据集为 Dtrain=(x,y),其中,输入数据为 x,输出数据为 y.测试数据集 Dtest=(x*,y*),输入测试数据为 x*,预测输出 y*,那么[y,y*]T 的联合概率密度函数遵从如下的 GMM 模型: ) GP y y ( , ) , | *   i i M  i i 1   * * * iy y y ( , yyp    iyy      iy yyp y (          * iy y y y ( , ),  ) , * * * M  i i 1  Var y [ (13) (14) (15) 其中,i=[iy,iy*]T,     i  T ] , [ iy , * i iy M i  并且满足 1 i   1. 联合概率密度函数表示为 GP y ( * | y f , 2 y ( ),  i i ) 其中, i * |  y  y ( ) E y [ f 边缘密度 py 和条件密度 *|y yp 可分别利用公式(13)和公式(14)求得,y 的边缘密度函数为     iyy 1     iyy 2   i 1  iyy * iy y * iy y     y ] ] iy iy iy . | * * * * p y ( ) y   p * yy y y ( , * y )d   M GP y ( , i 1  i   iy iy , )
    乔少杰 等:一种基于高斯混合模型的轨迹预测算法 条件密度函数为 y yp | ( * * y | y )   M  i i 1  y GP y f ( ) ( , 2 y ( ),  i i ) 其中,混合权重计算公式如下:  i y ( )  GP y ( ,   iy iy , )  i GP y ( ,   iy iy ,  i M  i 1  ) 因此,y*关于 y 的回归函数,即,y*的预测值为 y ( )  对应的方差为 Var y [ v y ( )  y ] f  | * * E y [ | x y x , , * ]   M  i i 1  y f ( )  y ( ) i 1055 (16) (17) (18) *  (19) 公式(18)称为轨迹高斯混合回归模型,其基本思想是:首先,利用公式(16)对轨迹数据利用概率密度函数建 模,通过 GMM 对训练轨迹数据进行聚类分析;然后,利用 EM 算法估计相应参数,依据符合正态分布数据的条件 分布得到 M 个高斯分量的回归函数;最后,利用公式(18)将回归函数加权混合完成轨迹回归预测. y 2 ( )] y f ( ) y ( )[ 2  i y ( )    y ] [ f   2 i i  M  i i 1   M  i i 1  5 模型训练学习原理 使用 GMM 对复杂运动模式建模就是要准确估计模型的参数,GMM 参数估计最常用的一种方式是最大 似然估计(expectation-maximization,简称 EM).EM 算法在迭代中改善模型参数估计,在每次迭代中不断地增加 模型估计参数与观测训练轨迹 X 方向矢量 xi(由若干轨迹点构成)的匹配概率.这里讨论 X 方向,Y 方向情况类 似.即,每次迭代使公式(11)达到 P(X|k+1)>P(X|k),其中,k 表示迭代的次数.通过不断地学习,获得最佳匹配训练 轨迹矢量集 X={x1,x2,...,xn}.迭代训练的目的即为找到一组,使得 P(X|)最大,如公式(20)所示: argmax ( P X ˆ   )  (20) |  求解使 P(X|)达到最大的参数值的过程如下: 为了便于求解,通常利用 logP(X|)代替 P(X|)求取最大值.文中 GMM 模型可以解释为对具有不同典型运 动模式的轨迹建模,单个高斯过程 GP()分量表示某一种简单运动模式出现的概率. P(X|)是参数的非线性函数,直接求其最大值非常困难,可以将公式(11)转化为下式进行间接求取: 其中, 方向上的特征矢量 x 属于第 i 种运动模式的概率密度.于是,对公式(21)进行运算,得到: (21) 为模型的另一组参数,i=1,2,...,M 为混合分量序号,p(x,i|)表示在参数条件下,一条轨迹在 X }      i p x i )log ( , ) ( ,   p x i ( , { ,  i )    ,  i  J  | |   M i 1  J ) ( ,    J ( , )    M i 1  p x i ( , |  p x i ){log ( , | )    p x i log ( , | )}   M  i 1  p x i ( , |  )log p x i ( , p x i ( , | | )   )  (22) 对于函数 f(x)=logx,具有性质:该函数在点(x,f(x))|x=1 处切线方程为(x)=x1.于是,f(x)≤(x),且当 x=1 时等号 成立.对于公式(22),有: J ) ( ,    J ( , )  ≤ M  i 1  p x i ( , | )  p x i ( , p x i ( , | | )   )       1     M p x i { ( , i 1  | )    p x i ( , | )}  (23) 记为 (24) 当且仅当=时等号成立.显然,只要 p(x,)
    分享到：
    赞 收藏

    相关推荐

    资料库

    行业

    共收录7266份资料，累计15个分类，关注成员有19位，主要包括：物流,旅游,餐饮零售,网络游戏,咨询,金融,电子政务,外包,教育,制造,医疗,嵌入式,互联网,交通,电信

    热门标签

    物流 旅游 餐饮零售 网络游戏 咨询 金融 电子政务 外包 教育 制造 医疗 嵌入式 互联网 交通 电信

    最新资料