第1页 / 共6页
第2页 / 共6页
第3页 / 共6页
第4页 / 共6页
第5页 / 共6页
第6页 / 共6页
传感器作业-非线性校正（查表法）.docx
某一传感器的输出-输入关系为：U = e0.01x - 1，输出量程范围为：0~5V，试采用查表法
作业 7
对其进行非线性校正，校正的精度要求为 1% 。
答：查表法
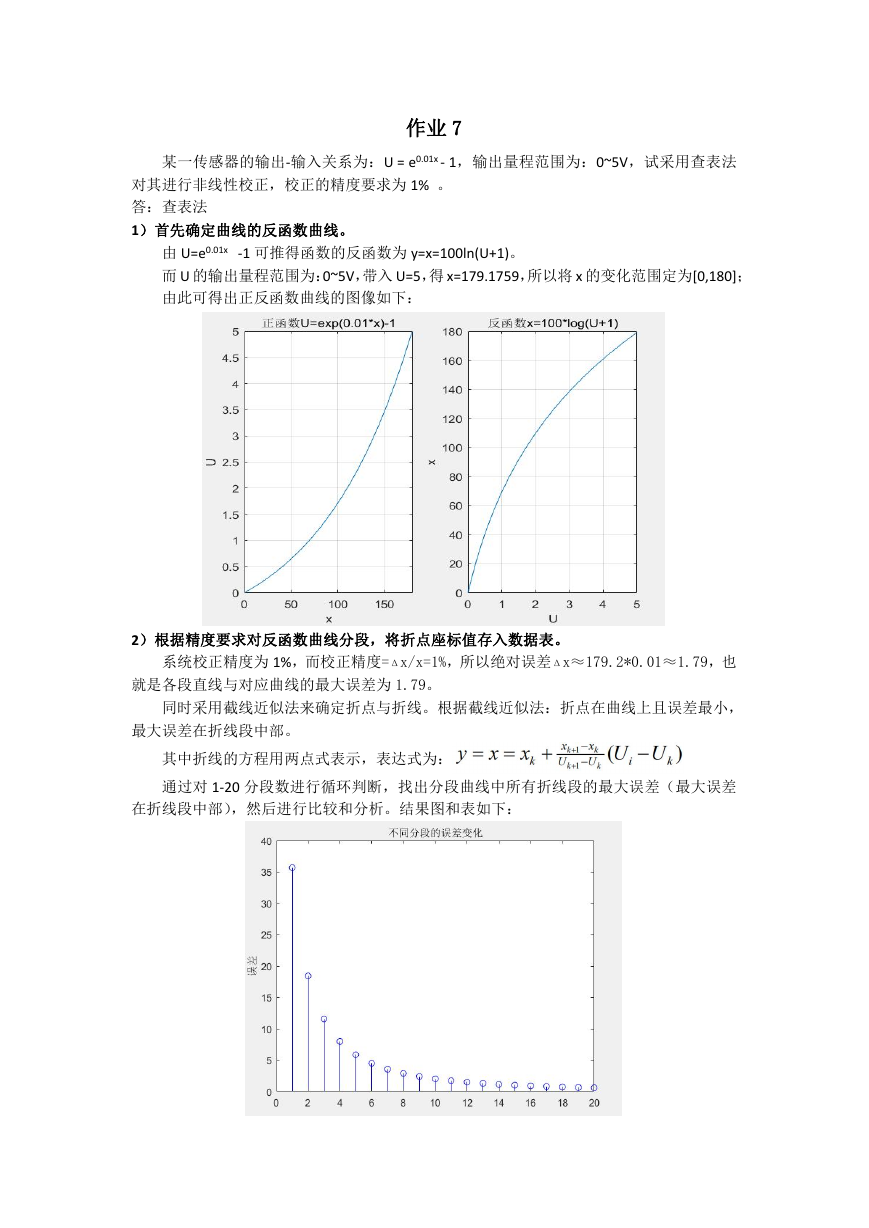
1）首先确定曲线的反函数曲线。
-1 可推得函数的反函数为 y=x=100ln(U+1)。
由 U=e0.01x
而 U 的输出量程范围为：0~5V，带入 U=5，得 x=179.1759，所以将 x 的变化范围定为[0,180]；
由此可得出正反函数曲线的图像如下：
2）根据精度要求对反函数曲线分段，将折点座标值存入数据表。
系统校正精度为 1%，而校正精度=Δx/x=1%，所以绝对误差Δx≈179.2*0.01≈1.79，也
就是各段直线与对应曲线的最大误差为 1.79。
同时采用截线近似法来确定折点与折线。根据截线近似法：折点在曲线上且误差最小，
最大误差在折线段中部。
其中折线的方程用两点式表示，表达式为：
通过对 1-20 分段数进行循环判断，找出分段曲线中所有折线段的最大误差（最大误差
在折线段中部），然后进行比较和分析。结果图和表如下：
35.688
1
分段数
Maxerr
分段数 11
Maxerr
1.7477
2
3
4
5
6
7
8
9
10
18.454
11.575
8.0043
5.8892
4.5212
3.5861
2.9180
2.4237
2.0411
12
13
14
15
16
17
18
19
20
1.5109
1.3202
1.1604
1.0292
0.9241
0.8281
0.7503
0.6799
0.6211
所以，当各折线段与对应曲线的最大误差小于 1.79 时即可满足系统所要求的精度要求，
针对上述所求结果可得出：当分段数为 11 时，即可满足系统要求，所以以下分段数选择 11。
由 c=roundn(5/11,-3)可得步长为 c=0.455。
接下来，由分段数为 11，段间距为 0.455，可以对 xi,Ui 进行初始化。如下表：
12
5.005
6
2.275
8
3.185
10
4.095
2
0.455
7
2.73
3
0.91
4
1.365
5
1.82
0
37.50
64.71
86.08
103.7
118.6
131.6
143.2
153.5
162.8
171.4
179.3
9
3.64
11
4.55
1
0
折点
Ui
xi
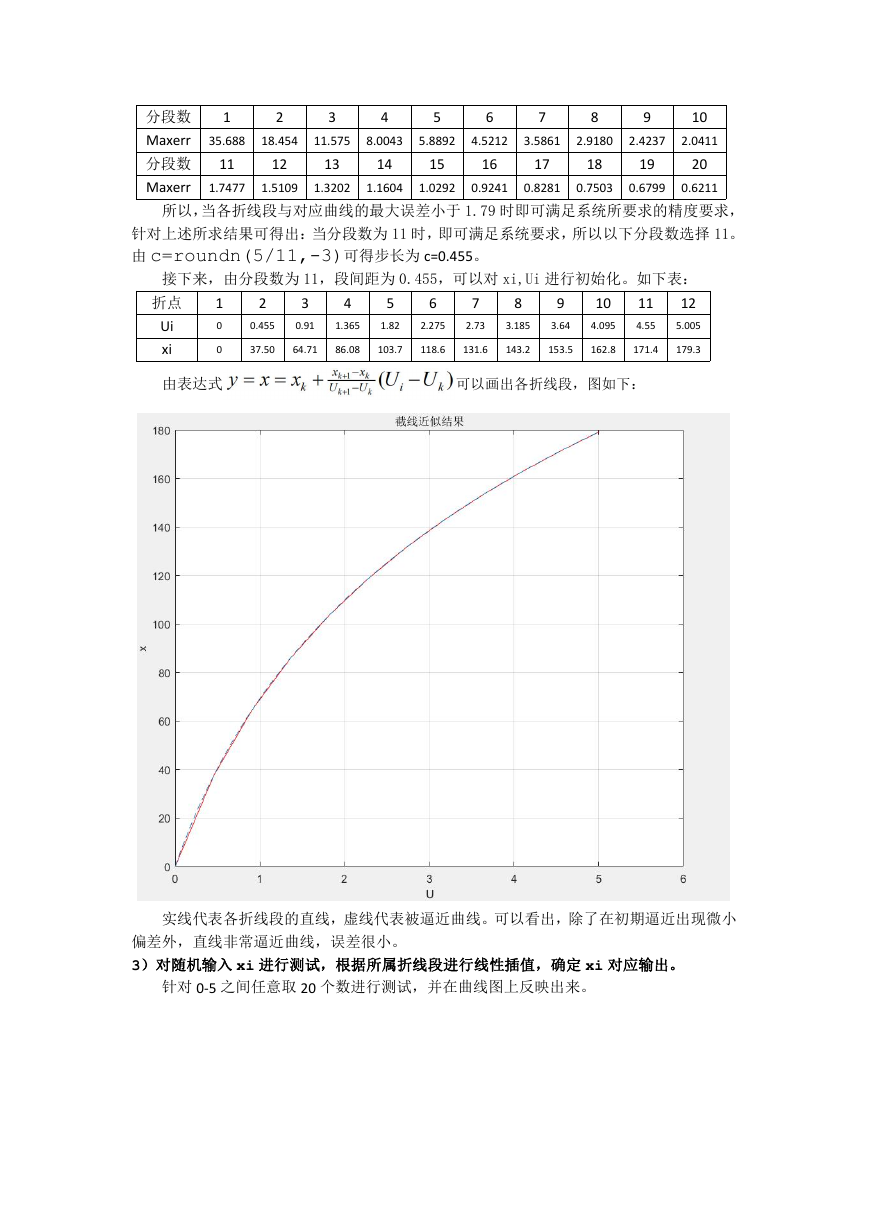
由表达式
可以画出各折线段，图如下：
实线代表各折线段的直线，虚线代表被逼近曲线。可以看出，除了在初期逼近出现微小
偏差外，直线非常逼近曲线，误差很小。
3）对随机输入 xi 进行测试，根据所属折线段进行线性插值，确定 xi 对应输出。
针对 0-5 之间任意取 20 个数进行测试，并在曲线图上反映出来。
序号
Ui
X
Xi
误差
精度
序号
Ui
X
Xi
误差
精度
1
0.344
29.5673
28.3546
1.2127
0.67%
7
3.5918
152.427
152.378
0.0491
0.03%
2
1.598
95.4741
95.0884
0.3857
0.21%
8
4.8432
176.529
176.458
0.0706
0.04%
3
2.6543
129.591
129.477
0.114
0.06%
9
2.6567
129.655
129.544
0.1111
0.06%
4
3.2722
145.214
145.129
0.0843
0.05%
10
1.6257
96.536
96.161
0.3751
0.21%
5
2.0381
111.123
110.844
0.2795
0.16%
11
0.5281
42.406
41.875
0.5307
0.29%
6
4.0999
162.92
162.918
0.004
0
12
3.0548
139.99
139.86
0.1331
0.07%
由表格可以看出，0-5 范围内随机产生的 12 个有效数据通过查表法得到的误差均小于
1.8，精度均小于 1%，由此可得此查表法的设计精度得到验证。
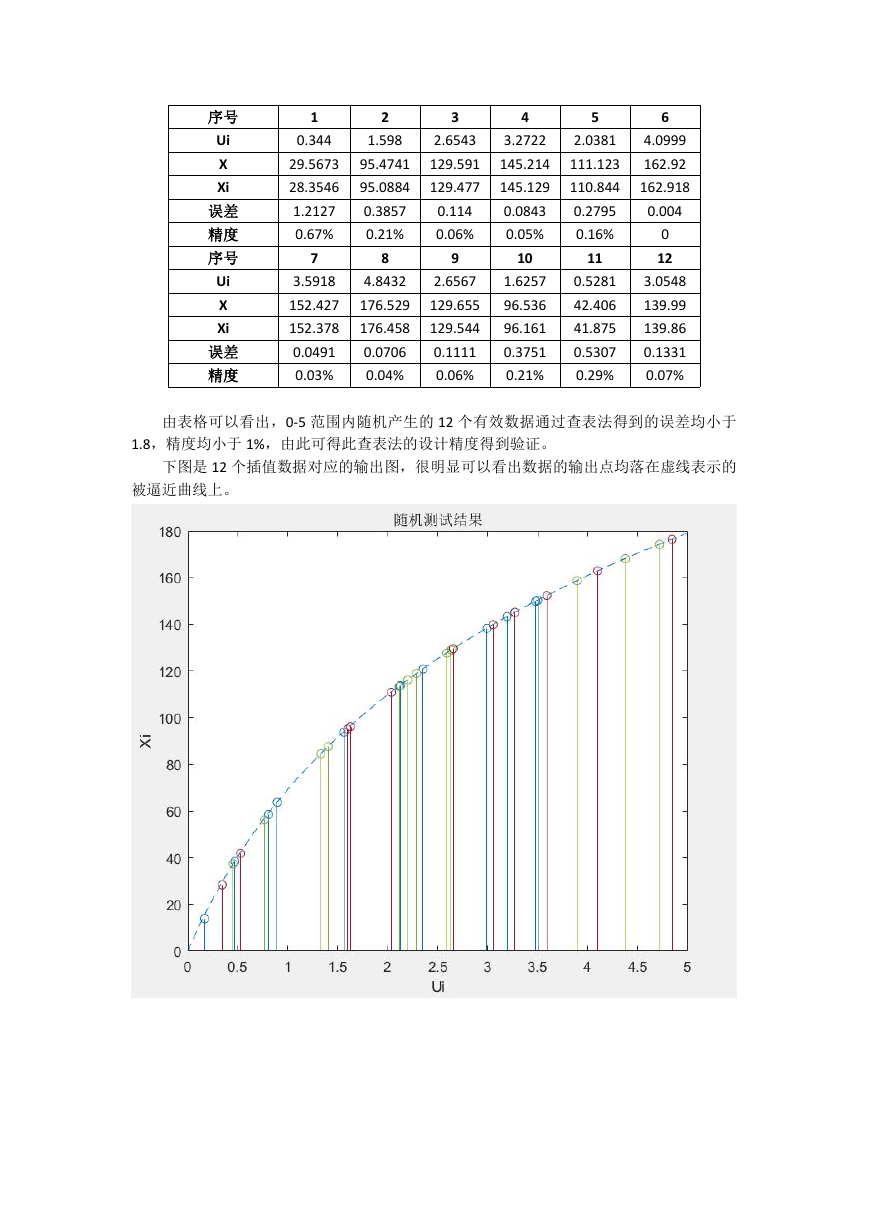
下图是 12 个插值数据对应的输出图，很明显可以看出数据的输出点均落在虚线表示的
被逼近曲线上。
Matlab 参考程序：
%确定反函数曲线 x=g(U)
x=0:180;
U=exp(0.01*x)-1;
subplot(1,2,1);
plot(x,U);
axis([0 180 0 5]) %U=f(x)
xlabel('x')
ylabel('U')
title('正函数 U=exp(0.01*x)-1')
grid on
subplot(1,2,2);
U=0:0.25:5;
x=100*log(U+1);
plot(U,x);
axis([0 5 0 180])
xlabel('U')
ylabel('x')
title('反函数 x=100*log(U+1)')
hold on
grid on
%x=g(U)
%不同分段的误差变化，选择合适分段数
for k=0:20
n=0;
c=roundn(5/k,-3);
for i=0:c:5
x=100*log(i+0.5*c+1);
xk=100*log(i+1);
xk1=100*log(i+c+1);
xi=xk+(xk1-xk)*(0.5*c)/c;
err(n+1)=x-xi;
n=n+1;
end
maxerr(k+1)=max(err);
end
t=0:20;
maxerr
stem(t,maxerr,'b')
title("不同分段的误差变化");
ylabel('误差');
%截线近似结果
for k=0:10
%总共 11 段
c=roundn(5/11,-3)
ui=c*k:0.005:c*(k+1)
uk=c*k
uk1=c*(k+1)
xk=100*log(uk+1)
xk1=100*log(uk1+1)
xi=xk+(xk1-xk)*(ui-uk)/(uk1-uk)
plot(ui,xi,'r','linewidth',0.2);
hold on
grid on
end
t=0:0.01:5;
y=100*log(t+1);
plot(t,y,'--')
hold on
title("截线近似结果");
xlabel("U");
ylabel("x");
%折点坐标表
c=roundn(5/11,-3)
for k=0:12
ui=c*k
xi=100*log(c*k+1)
end
%随机数据的验证测试
clc
Ui=5*rand(1,12);
Xi=zeros(1,12);
X=100*log(Ui+1);
c=roundn(5/11,-3);
u=0:c:5.005;
x=100*log(u+1);
for i=1:12
for j=1:11
if Ui(i)
a=Ui
b=X
c=Xi
d=X-Xi
e=(X-Xi)/180
stem(Ui,Xi)
xlabel('Ui');
ylabel('Xi');
hold on
t=0:0.01:5;
y=100*log(t+1);
plot(t,y,'--')
hold on
title('随机测试结果');
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
