第1页 / 共10页
第2页 / 共10页
第3页 / 共10页
第4页 / 共10页
第5页 / 共10页
第6页 / 共10页
第7页 / 共10页
第8页 / 共10页
RSA实现算法报告关于RSA算法的实现代码.doc
实 验 报 告
姓名：XXXXXXXXX 学号：0XXXXX 班级：XXXXXXXXX 日期：2013/12/*
题目：RSA 算法实验
一、实验环境
1．硬件配置：
处理器：Inter(R) Core(TM) i5-2430M CPU @ 2.40GHz (4 CPUs) ,~2.4GHz
内存：2048MB RAM
2．使用软件：
(1) 操作系统：win7 旗舰版
(2) 软件工具：Microsoft Visual c++ 6.0
二、实验涉及的相关概念或基本原理
它是第一个既能用于数据加密也能用于数字签名的算法。算法的名字以发明者的名字命名：Ron
Rivest, Adi Shamir 和 Leonard Adleman。但 RSA 的安全性一直未能得到理论上的证明。它经历了各种攻
击，至今未被完全攻破。
RSA 的安全性依赖于大数分解。公钥和私钥都是两个大素数（ 大于 100 个十进制位）的函数。
从一个密钥和密文推断出明文的难度等同于分解两个大素数的积。
密钥对的产生。选择两个大素数，p 和 q 。计算：
n = p * q
然后随机选择加密密钥 e，要求 e 和 ( p - 1 ) * ( q - 1 ) 互质。最后，利用 Euclid 算法计算解密密钥 d,
满足
e * d = 1 ( mod ( p - 1 ) * ( q - 1 ) )
其中 n 和 d 也要互质。数 e 和 n 是公钥，d 是私钥。两个素数 p 和 q 不再需要，应该丢弃，不要让
任何人知道。
加密信息 m（二进制表示）时，首先把 m 分成等长数据块 m1 ,m2,..., mi ，块长 s ，其中 <= n, s 尽
可能的
大。对应的密文是：
ci = mi^e ( mod n ) ( a )
解密时作如下计算：
mi =ci^d ( mod n ) ( b )
RSA 可用于数字签名，方案是用 ( a ) 式签名， ( b )式验证。具体操作时考虑到安全性和 m 信息量
较大等因素，一般是先作 HASH 运算。
RSA 的安全性。 RSA 的安全性依赖于大数分解，但是否等同于大数分解一直未能得到理论上的证
明，因为没有证明破解 RSA 就一定需要作大数分解。假设存在一种无须分解大数的算法，那它肯定可以
修改成为大数分解算法。目前， RSA 的一些变种算法已被证明等价于大数分解。不管怎样，分解 n 是
最显然的攻击方法。现在，人们已能分解多个十进制位的大素数。因此，模数 n 必须选大一些，因具体
适用情况而定。
RSA 的速度。 由于进行的都是大数计算，使得 RSA 最快的情况也比 DES 慢上倍，无论是软件还是
硬件实现。速度一直是 RSA 的缺陷。一般来说只用于少量数据加密。
RSA 的选择密文攻击。 RSA 在选择密文攻击面前很脆弱。一般攻击者是将某一信息作一下伪装( Blind)，
让拥
有私钥的实体签署。然后，经过计算就可得到它所想要的信息。实际上，攻击利用的都是同一个弱
点，即存在这样一个事实：乘幂保留了输入的乘法结构：
( XM )^d = X^d *M^d mod n
前面已经提到，这个固有的问题来自于公钥密码系统的最有用的特征--每个人都能使用公钥。但从算
法上无法解决这一问题，主要措施有两条：一条是采用好的公钥协议，保证工作过程中实体不对其他实
体任意产生的信息解密，不对自己一无所知的信息签名；另一条是决不对陌生人送来的随机文档签名，
签名时首先使用 One-Way HashFunction 对文档作 HASH 处理，或同时使用不同的签名算法。在中提到了
几种不同类型的攻击方法。
RSA 的公共模数攻击。 若系统中共有一个模数，只是不同的人拥有不同的 e 和 d，系统将是危险的。
最普遍的情况是同一信息用不同的公钥加密，这些公钥共模而且互质，那末该信息无需私钥就可得到恢
复。设 P 为信息明文，两个加密密钥为 e1 和 e2，公共模数是 n，则：
C1 = P^e1 mod n
C2 = P^e2 mod n
密码分析者知道 n、e1、e2、C1 和 C2，就能得到 P。 因为 e1 和 e2 互质，故用 Euclidean 算法能找到 r
和 s，满足：
r * e1 + s * e2 = 1
假设 r 为负数，需再用 Euclidean 算法计算 C1^(-1)，则
( C1^(-1) )^(-r) * C2^s = P mod n
另外，还有其它几种利用公共模数攻击的方法。总之，如果知道给定模数的一对 e 和 d，一是有利于
攻击者分解模数，一是有利于攻击者计算出其它成对的 e’和 d’，而无需分解模数。解决办法只有一个，
那就是不要共享模数 n。
RSA 的小指数攻击。 有一种提高 RSA 速度的建议是使公钥 e 取较小的值，这样会使加密变得易于
实现，速度有所提高。但这样作是不安全的，对付办法就是 e 和 d 都取较大的值。
三、实验内容
主要的方法：
（1）、public static void GetPrime()
方法名称：产生大数的方法。
说明：
利用 Java 语言的中的 java.math.BigInteger 类的方法中随机产生大数。
（2）、public static boolean MillerRobin(BigInteger num)
方法名称：判断是否是素数的方法。
参数说明：
num 是由 GetPrime 方法产生的大数。
说明：
这个方法判断 GetPrime 方法传过来的是否是一个素数，是就返回 true,否就返回 false。
（3）、public static BigInteger powmod( BigInteger a, BigInteger t, BigInteger num )
方法名称：大数的幂运算方法。
说明：
这个方法对传入的大数进行幂运算。
（4）、public static BigInteger invmod(BigInteger a, BigInteger b)
方法名称：大数的取模运算方法。
说明：这个方法对大数进行取模运算。
（5）、public static String Encode(String inStr,BigInteger PrimeP,BigInteger PrimeQ,
BigInteger n,int nLen,int m,JTextField d)
方法名称：加密算法。
参数说明：
inStr 是从界面输入的明文。
PrimeP 和 PrimeQ 是由 GetPrime 方法产生的两个大素数。
n 是由 PrimeP 和 PrimeQ 得到的值。
nLen 为 n 的长度。
d 为公钥。
（6）、public static String Decode(String inStr,BigInteger PrimeP,BigInteger PrimeQ,
BigInteger n,int nLen,int m,JTextField e)
方法名称：解密算法。
参数说明：
inStr 是从界面输入的明文。
PrimeP 和 PrimeQ 是由 GetPrime 方法产生的两个大素数。
n 是由 PrimeP 和 PrimeQ 得到的值。
nLen 为 n 的长度。
e 为私钥。
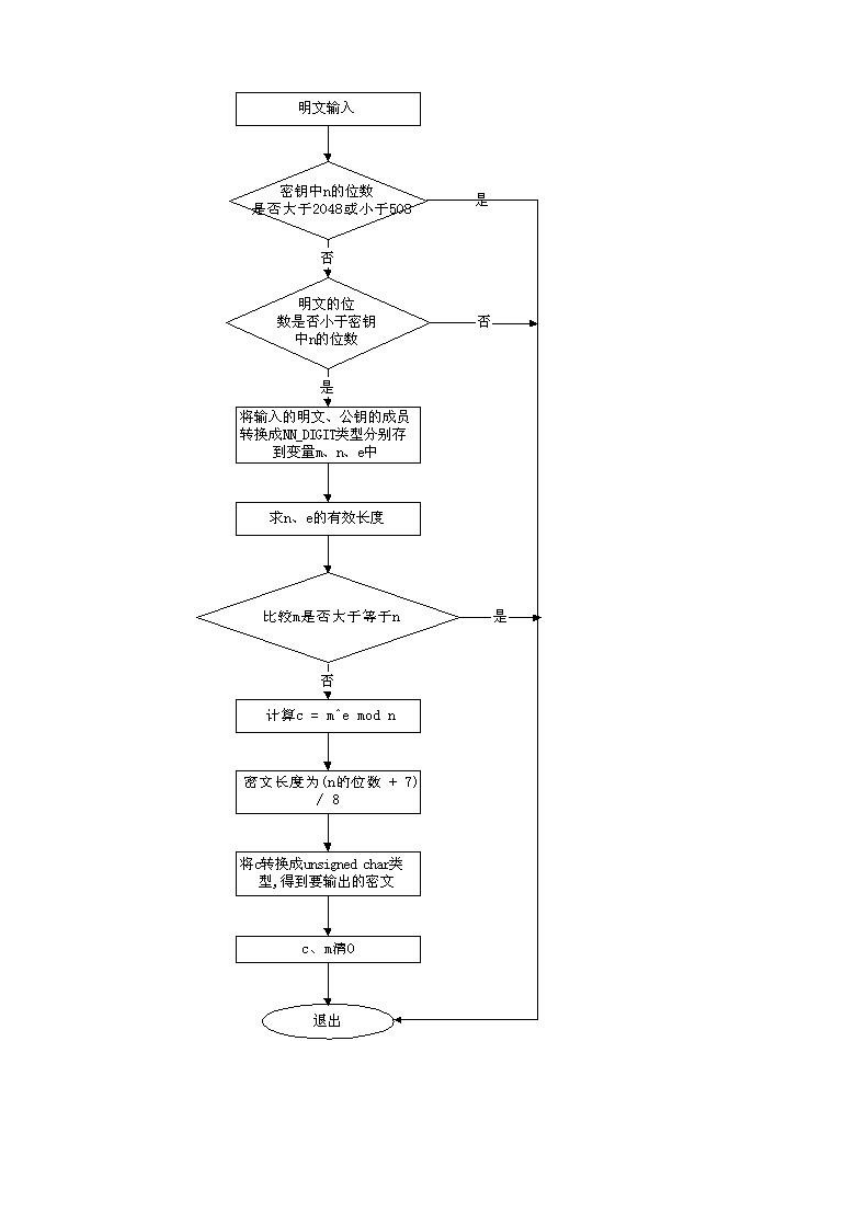
流程图：
RSA 公钥加密算法流程图：
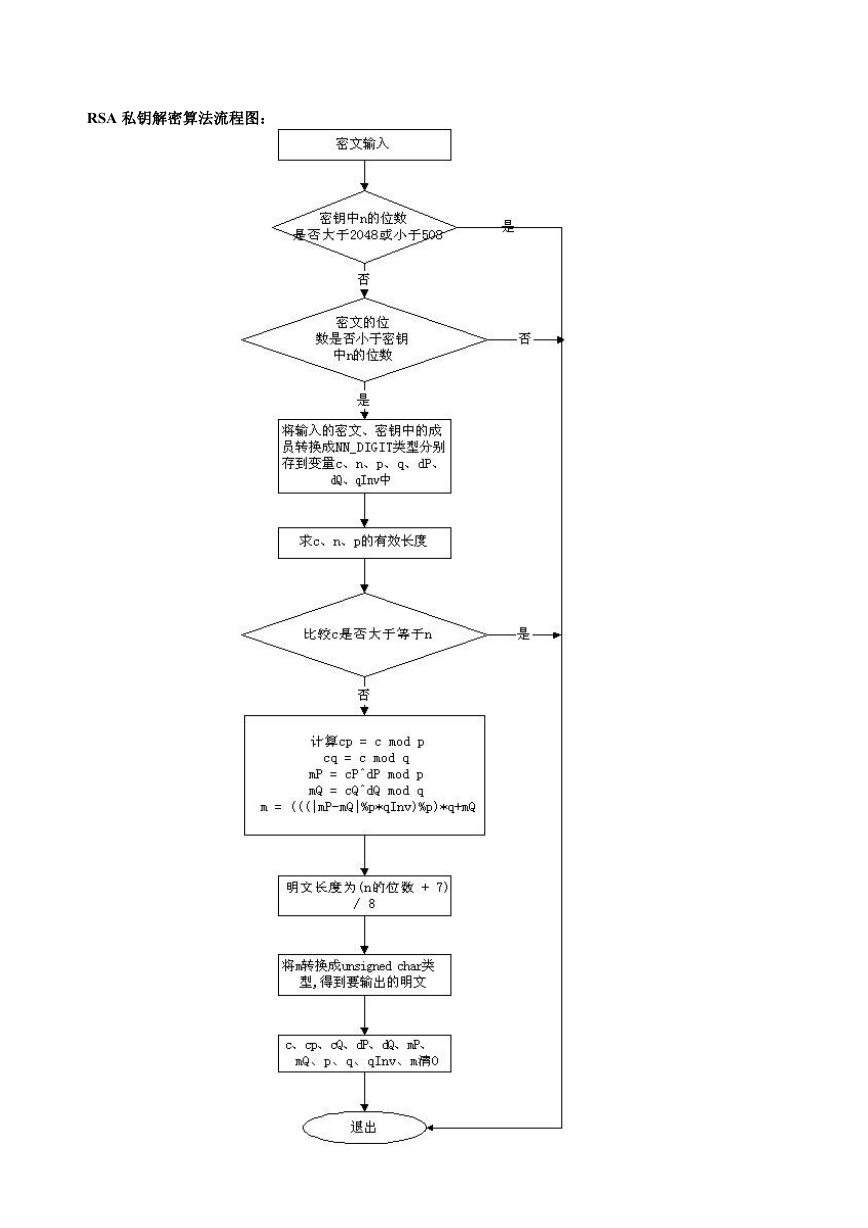
RSA 私钥解密算法流程图：
主要代码：
1 判定一个数是否为素数
bool test_prime(Elemtype m){
if(m<=1){
return false;
}
else if(m==2){
return true;
}
else{
for(int i=2;i<=sqrt(m);i++){
if((m%i)==0){
return false;
break;
}
}
return true;
}
②将十进制数据转化为二进制数组
void switch_to_bit(Elemtype b,Elemtype bin[32]){
int n=0;
while(b>0){
bin[n]=b%2;
n++;
b/=2;
}
③求最大公约数
Elemtype gcd(Elemtype a,Elemtype b){
order(a,b);
int r;
if(b==0){
return a;
}
else{
while(true){
r=a%b;
a=b;
b=r;
if(b==0){
return a;
break;
}
}
}
④用扩展的欧几里得算法求乘法逆元
Elemtype extend_euclid(Elemtype m,Elemtype bin){
order(m,bin);
Elemtype a[3],b[3],t[3];
a[0]=1,a[1]=0,a[2]=m;
b[0]=0,b[1]=1,b[2]=bin;
if(b[2]==0){
return a[2]=gcd(m,bin);
}
if(b[2]==1){
return b[2]=gcd(m,bin);
}
while(true){
if(b[2]==1){
return b[1];
break;
}
int q=a[2]/b[2];
for(int i=0;i<3;i++){
t[i]=a[i]-q*b[i];
a[i]=b[i];
b[i]=t[i];
}
}
⑤快速模幂算法
Elemtype modular_multiplication(Elemtype a,Elemtype b,Elemtype n){
Elemtype f=1;
Elemtype bin[32];
switch_to_bit(b,bin);
for(int i=31;i>=0;i--){
f=(f*f)%n;
if(bin[i]==1){
f=(f*a)%n;
}
}
return f;
}
⑥产生密钥
void produce_key(){
cout<<"输入素数 p 和 q:";
cin>>p>>q;
while(!(test_prime(p)&&test_prime(q))){
cout<<"输入错误，请重新输入!"<>p>>q;
};
pr.n=p*q;
pu.n=p*q;
fn=(p-1)*(q-1);
cout<<"fn 为："<>e;
while((gcd(fn,e)!=1)){
cout<<"e 输入错误，请重新输入!"<>e;
}
pr.d=(extend_euclid(fn,e)+fn)%fn;
pu.e=e;
flag=1;
cout<<"公钥(e,n）:"<
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
