论文研究-基于Laurent分解实现多进制CPM信号的相干检测 .pdf-资料库

基于Laurent分解实现多进制CPM信号的相干检测 http://www.paper.edu.cn 杨剑锋1 ，张长明1，张波2，陈颖2 1 电子科技大学，四川成都（610054） 2 中国西南电子技术研究所，四川成都（610036）摘要：基于扩展 Laurent 分解，可以把任意连续相位调制（CPM）信号表示成一系列脉冲幅度调制(PAM)信号之和。根据这一方法提出了一种可以减少 CPM 最大似然序列检测（MLSD）复杂性的最优化算法及次优化算法。用 4 进制部分响应 CPM 系统实现了这两种算法，证明了可以明显减少接收端信号检测的复杂性，比较了最优化算法和次优化算法的码元误码率性能。关键词：连续相位调制，Laurent分解，最大似然估计，维特比算法 1. 引言连续相位调制（CPM）是一种非线性数字调制方案，是把信息加载到相位上，并确保相位是时间的连续函数的一种调制方法。在无线传输中，CPM具有良好的传输持性，它的功率和带宽具有非常高的效率；另外，它产生的传输波形是具有连续恒包络特性的。这样, 在接收端可以使用成本较低的非线性放大器。当然，由于非线性的特点使得CPM信号在接收端的检测和分析也具有一定的复杂性。在通信系统中，降低系统的复杂性和系统成本一直是方案设计的主要目标之一。本文研究的问题正是基于这一设计目标，提出了两种信号检测方法——最优化算法和次优化算法。并用这两种方法在软件平台上实现了四进制部分响应CPM系统的相干检测，通过比较这两种算法的误码率性能，以及这两种算法和MLSD算法所需要的匹配滤波器个数及所需维特比译码的状态个数，证实了这两种算法同传统的MLSD相比，对系统复杂性及系统成本具有巨大的降低作用。 2. CPM 信号模型及分解假调单信号调制指数，复包络CPM信号可以表示成如下低通等效形式： ts )( = 2 E T ϕ at ;( ) = h 2 π 1 − Ns ∑ i 0 = Ns 1 − ∑ = LNs − = θ Ln − + h 2 π i tqa ( i − iT ) j ϕ at ,( ) S e (1) tqa ( i − iT ) = h π LNs 1 −− a ∑ i = 0 + h 2 π i i 1 − Ns ∑ = LNs − tqa ( i − iT ) (2) ( − )1 M 其中,T 表示码元持续时间, ......, 3,1 ±± sE 表示每码元的能量, h 表示调制指数, ± ia 表示 M 进制符 }, Ns 表示非相关序列 ia 的长度, L 表示相位关号信息并且属于集合{ 联长度,且为大于等于1的整数。当 L 等于1时，系统称为全响应CPM系统，当 L 大于1时，系统称为部分响应CPM系统。相位响应函数 )(tq 是脉冲函数 )(tg 的积分, 脉冲函数 )(tg 通常取矩形脉冲REC(3式)、升余弦脉冲RC(4式)、以及高斯最小相移键控脉冲GMSK(略)等。 )(tg 和 )(tq 分别具有如下定义: 作者简介：杨剑锋(1982-)，男，硕士研究生，主要从事通信调制解调、信号处理方面的研究。 -1-

REC： tg )( = t 0, ≤≤ 1 ⎧ ⎪ LT 2 ⎨ ⎪⎩ otherwise ,0 LT ⎫ ⎪ ⎬ ⎪⎭ (3) RC： tg )( = tq )( ∫= τ g ττ0 )( d (5) tq )( = ⎧ ⎪ ⎨ ⎪⎩ ,0 1 2 t < (6) , t ≥ LT http://www.paper.edu.cn t 2 π LT 0)], ≤≤ t LT (4) ⎫ ⎪ ⎬ ⎪⎭ cos( − 1[ 1 ⎧ ⎪ LT 2 ⎨ ⎪⎩ otherwise ,0 0 把CPM信号分解成多个PAM信号之和是一种克服CPM非线性特点的有效有手段，这种方法可以有效的减小CPM解调的复杂性。1986年，Pierre A. Laurent 证明了任何一种二进制连续相位调制（CPM）信号都可以表示成为有限个脉冲幅度调制(PAM)信号之和的形式[1]。然后1995年，Umberto Mengali 和 Michele Morelli 把这种可以用有限个PAM信号之和来表示CPM信号的方法推广到多进制的连续相位调制（包括部分响应CPM信号）系统[2]。使用这种分解方法，可以有效的减少CPM接收端检测模块的复杂性。并且，由于这种分解方法是对CPM信号的准确分解，所在解调时并不会造系统误码率性能的下降，而是保持和传统的MLSD方法相同的误码率性能，称这种方法为最优化算法。为了可以进一步减少CPM信号解调的复杂性，往往并不使用全部的PAM信号来进行处理，而是选用其中包含CPM信号信息量最多的几个PAM信号来逼近CPM信号，同时保持系统的误码率性能和使用最优化算法的系统相比只是非常有限的降低，称这种方法为次优化算法。次优化算法可以有效的减少解调模块中匹配滤波器个数的同时，还可以减少维特比状态的个数，从而大大的减少了相干检测的复杂性。 N − ∑ K = Ns − ∑ n 0 = tS )( nT 1 a − = g nk , ) ( t 1 0 k (7) p , p = − M 2 Q )1 2( log= 12 − = L pQN 个PAM信号之和,其中根据Laurent分解表达式[2], 当调制指数h是非整数有理数时，复包络CPM信号可以精确 ,表达式如(7)式所示。的表示成系数 nka , 称为假设码元，脉冲函数 )(tg k 称为Laurent函数(LF)，持续时间为[T,(L+1)T]。 nka , 是符号信息 ia 的函数； kg 由调制指数 h 、关联长度 L 、以及进制数 M 共同决定，并且可以表示成多个时间有限的脉冲信号之积的形式。这两个参数都需要大量的计算来获取，在文献[2]中详细描述了多进制情况下对这两个参数的计算。当调制指数是整数和无理数时，CPM 信号也可以表示成有限个PAM信号之和的形式，但是表示形式和(4)式不完全一样。鉴于绝大多数情况下的CPM系统的调制指数都是小于1的有理数，所以这里仅讨论调制指数为小于 1的有理数的情况。 3. 连续相位调制的相干检测 3.1 最优化相干检测假设系统信道为加性高斯白噪声信道（AWGN），载波同步和位同步都已准确的建立，接收到的 CPM 信号可以表示为如下低通形式： = + ts )( tn )( tr )( )(tn 为零均值二阶高斯白噪声，双边功率谱密度为（8），与基带信号 )(ts 相互独立且 2/0N 具有相同的带宽。由于所有可能传输的信号都具有相同的能量和出现概率，所以根据相干检 -2-

测的要求，使相关表达式(9)具有最大值的序列 a 被认为是发送端传输的符号信息序列。 http://www.paper.edu.cn = ), tr ( Re{( ∫= δ i 把(7)式代入(9)式得： ))} ts ( Re{ str )( * t )}( dt (9) δ i = E s T Ns 1 − λ ∑ i n 0 = n )( （ 10 ） nλ )( i = Re{ N 1 − ar ,∑ nk k 0 = * nk , } r nk , = tr )([ ∗ g ∗ ( − t )] = ∫ gtr )( k t = nT * ( t − nT ) dt (11) (12) p = − )1 2( pQN 通过(11)式可以看出，只需知道个 nkr , 和 nka , 的值就可以统计并判决，求出信息序列。从(12)式可以看出 nkr , 可以通过采样在 nT 时刻基带信号 )(tr 经过匹配滤波器 kg 的输出值得到，而由于 kg 具有实值，所以它的共轭值就等于它本身。计算 )(niλ 同样需要知道在 nT 时刻 nka , 的所有可能值， nka , 由符号信息 na 和状态向量决定 [2]。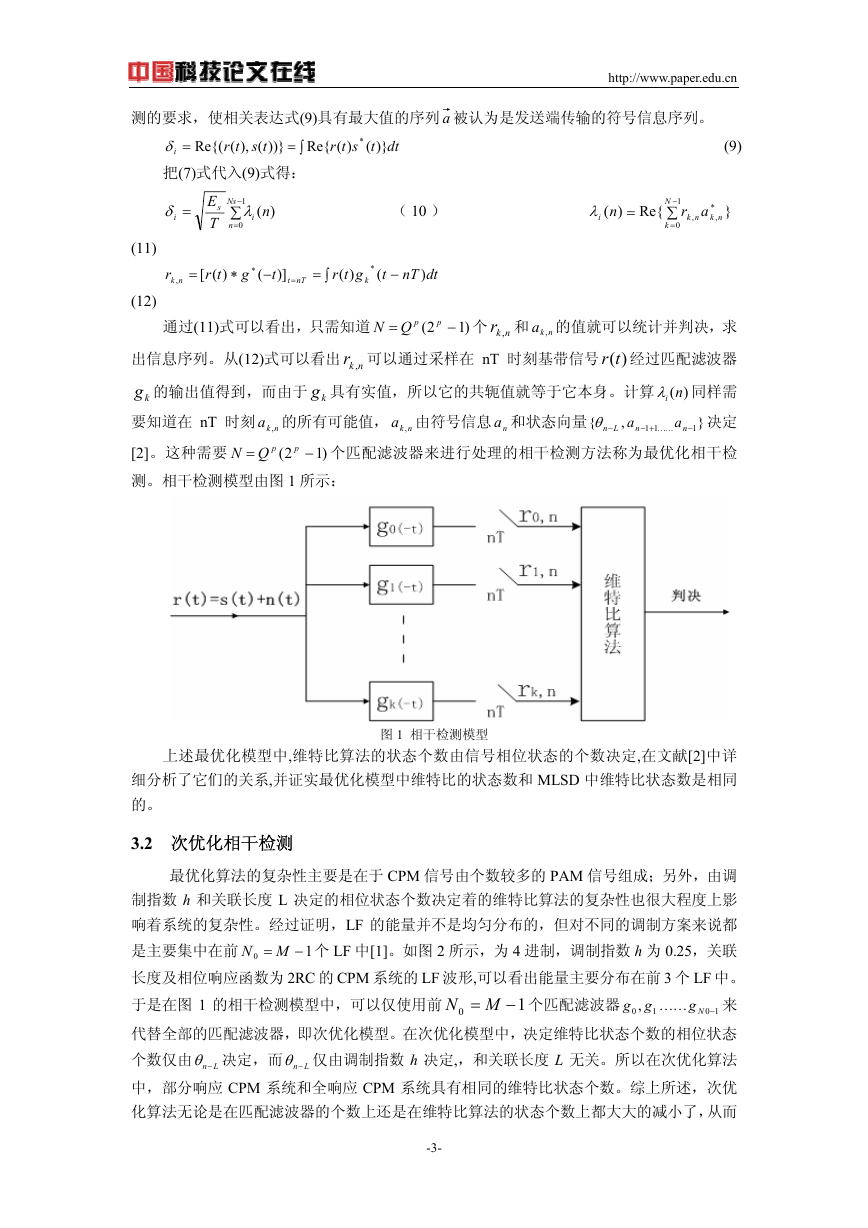这种需要测。相干检测模型由图 1 所示：个匹配滤波器来进行处理的相干检测方法称为最优化相干检 pQN aθ , { n 11 1 −……+− 2( )1 Ln − − = a } p n 图 1 相干检测模型上述最优化模型中,维特比算法的状态个数由信号相位状态的个数决定,在文献[2]中详细分析了它们的关系,并证实最优化模型中维特比的状态数和 MLSD 中维特比状态数是相同的。 3.2 次优化相干检测最优化算法的复杂性主要是在于 CPM 信号由个数较多的 PAM 信号组成；另外，由调制指数 h 和关联长度 L 决定的相位状态个数决定着的维特比算法的复杂性也很大程度上影响着系统的复杂性。经过证明，LF 的能量并不是均匀分布的，但对不同的调制方案来说都个 LF 中[1]。如图 2 所示，为 4 进制，调制指数 h 为 0.25，关联是主要集中在前长度及相位响应函数为 2RC 的 CPM 系统的 LF 波形,可以看出能量主要分布在前 3 个 LF 中。于是在图 1 的相干检测模型中，可以仅使用前个匹配滤波器 = MN = MN 来 −…… Ng 10 gg 0, − 1 − 1 1 0 0 代替全部的匹配滤波器，即次优化模型。在次优化模型中，决定维特比状态个数的相位状态个数仅由 Ln−θ 决定，而 Ln−θ 仅由调制指数 h 决定,，和关联长度 L 无关。所以在次优化算法中，部分响应 CPM 系统和全响应 CPM 系统具有相同的维特比状态个数。综上所述，次优化算法无论是在匹配滤波器的个数上还是在维特比算法的状态个数上都大大的减小了，从而 -3-

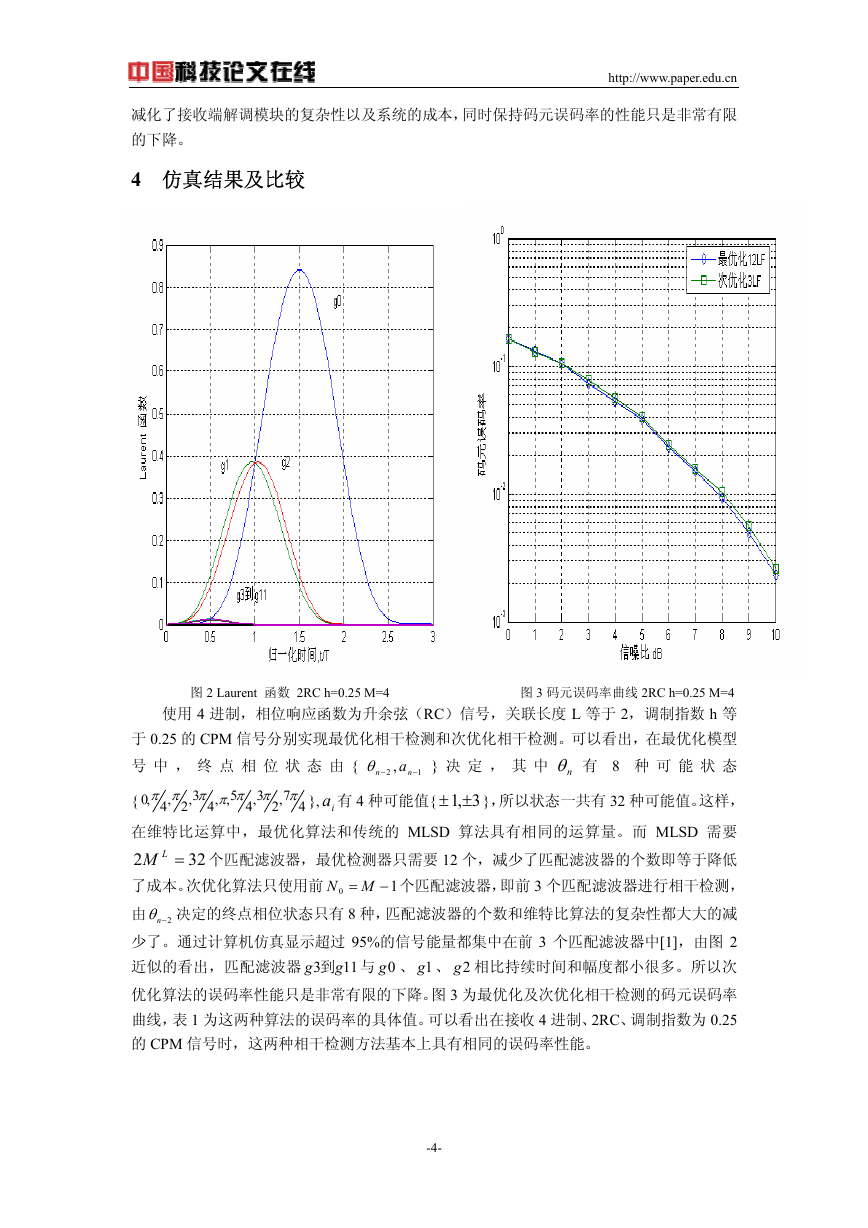
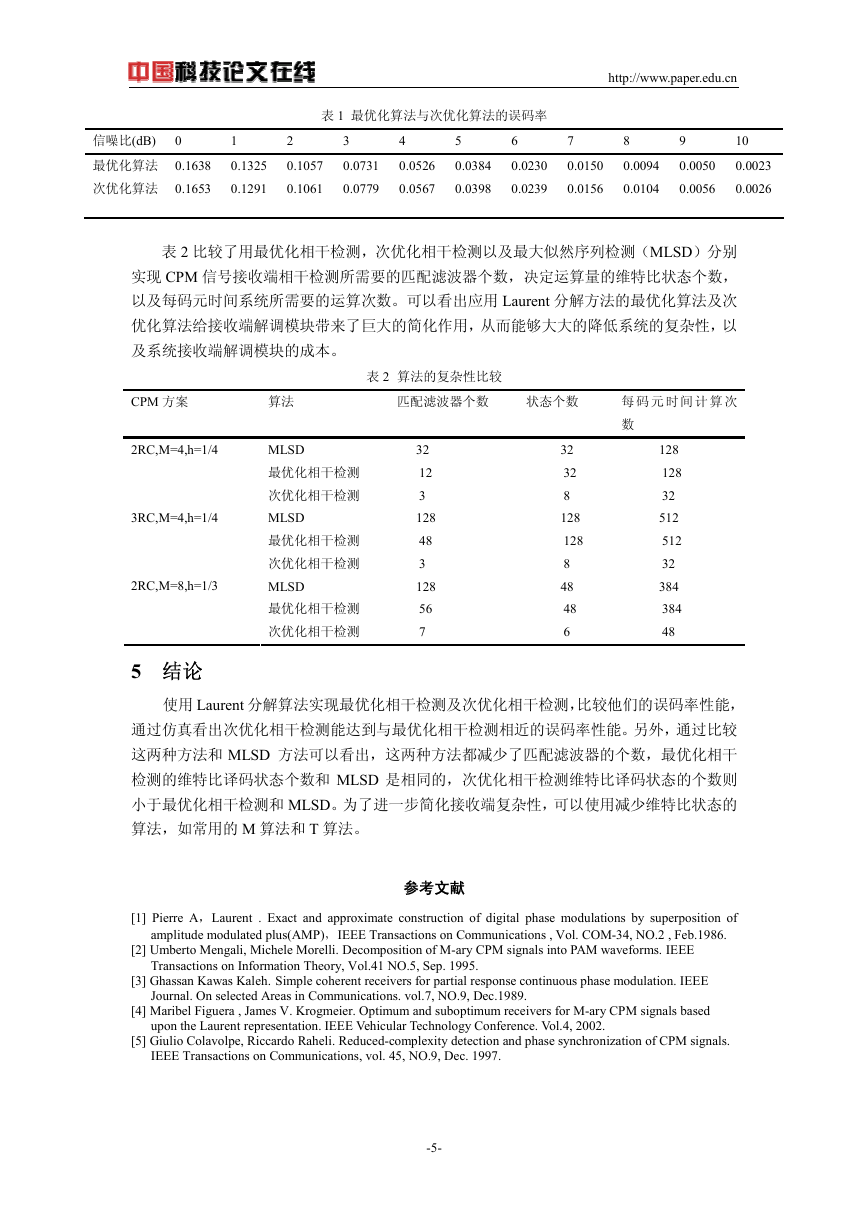
减化了接收端解调模块的复杂性以及系统的成本，同时保持码元误码率的性能只是非常有限的下降。 4 仿真结果及比较 http://www.paper.edu.cn { }, n 1 − 5, ,4 3,4 aθ 2 , n − =LM ia 有 4 种可能值{ 图 2 Laurent 函数 2RC h=0.25 M=4 图 3 码元误码率曲线 2RC h=0.25 M=4 使用 4 进制，相位响应函数为升余弦（RC）信号，关联长度 L 等于 2，调制指数 h 等于 0.25 的 CPM 信号分别实现最优化相干检测和次优化相干检测。可以看出，在最优化模型 } 决定，其中 nθ 有 8 种可能状态号中，终点相位状态由 { 3,2,4,0 7,2 πππππππ 3,1 ±± }，所以状态一共有 32 种可能值。这样， 4 在维特比运算中，最优化算法和传统的 MLSD 算法具有相同的运算量。而 MLSD 需要 2 个匹配滤波器，最优检测器只需要 12 个，减少了匹配滤波器的个数即等于降低个匹配滤波器，即前 3 个匹配滤波器进行相干检测，了成本。次优化算法只使用前由 2−nθ 决定的终点相位状态只有 8 种，匹配滤波器的个数和维特比算法的复杂性都大大的减少了。通过计算机仿真显示超过 95%的信号能量都集中在前 3 个匹配滤波器中[1]，由图 2 3 g g 到与 0g 、 1g 、 2g 相比持续时间和幅度都小很多。所以次近似的看出，匹配滤波器优化算法的误码率性能只是非常有限的下降。图 3 为最优化及次优化相干检测的码元误码率曲线，表 1 为这两种算法的误码率的具体值。可以看出在接收 4 进制、2RC、调制指数为 0.25 的 CPM 信号时，这两种相干检测方法基本上具有相同的误码率性能。 = MN 32 0 − 1 11 -4-

表 1 最优化算法与次优化算法的误码率信噪比(dB) 最优化算法次优化算法 0 0.1638 0.1653 1 0.1325 0.1291 2 0.1057 0.1061 3 0.0731 0.0779 4 0.0526 0.0567 5 0.0384 0.0398 6 0.0230 0.0239 7 0.0150 0.0156 8 0.0094 0.0104 9 0.0050 0.0056 10 0.0023 0.0026 http://www.paper.edu.cn 表 2 比较了用最优化相干检测，次优化相干检测以及最大似然序列检测（MLSD）分别实现 CPM 信号接收端相干检测所需要的匹配滤波器个数，决定运算量的维特比状态个数，以及每码元时间系统所需要的运算次数。可以看出应用 Laurent 分解方法的最优化算法及次优化算法给接收端解调模块带来了巨大的简化作用，从而能够大大的降低系统的复杂性，以及系统接收端解调模块的成本。 CPM 方案算法匹配滤波器个数状态个数表 2 算法的复杂性比较每码元时间计算次数 2RC,M=4,h=1/4 3RC,M=4,h=1/4 2RC,M=8,h=1/3 5 结论 MLSD 32 32 128 最优化相干检测 12 32 128 次优化相干检测 3 8 32 MLSD 128 128 512 最优化相干检测 48 128 512 次优化相干检测 3 8 32 MLSD 128 48 384 最优化相干检测 56 48 384 次优化相干检测 7 6 48 使用 Laurent 分解算法实现最优化相干检测及次优化相干检测，比较他们的误码率性能，通过仿真看出次优化相干检测能达到与最优化相干检测相近的误码率性能。另外，通过比较这两种方法和 MLSD 方法可以看出，这两种方法都减少了匹配滤波器的个数，最优化相干检测的维特比译码状态个数和 MLSD 是相同的，次优化相干检测维特比译码状态的个数则小于最优化相干检测和 MLSD。为了进一步简化接收端复杂性，可以使用减少维特比状态的算法，如常用的 M 算法和 T 算法。参考文献 [1] Pierre A，Laurent . Exact and approximate construction of digital phase modulations by superposition of amplitude modulated plus(AMP)，IEEE Transactions on Communications , Vol. COM-34, NO.2 , Feb.1986. [2] Umberto Mengali, Michele Morelli. Decomposition of M-ary CPM signals into PAM waveforms. IEEE [3] Ghassan Kawas Kaleh. Simple coherent receivers for partial response continuous phase modulation. IEEE Transactions on Information Theory, Vol.41 NO.5, Sep. 1995. Journal. On selected Areas in Communications. vol.7, NO.9, Dec.1989. [4] Maribel Figuera , James V. Krogmeier. Optimum and suboptimum receivers for M-ary CPM signals based upon the Laurent representation. IEEE Vehicular Technology Conference. Vol.4, 2002. [5] Giulio Colavolpe, Riccardo Raheli. Reduced-complexity detection and phase synchronization of CPM signals. IEEE Transactions on Communications, vol. 45, NO.9, Dec. 1997. -5-

http://www.paper.edu.cn The Coherent Detection for M-ary CPM Signals based on The Laurent Decomposition Yang jianfeng1，Zhang bo2，Chen ying2，Zhang changming1 1(University of Electronic Science and Technology of China, Chengdu 610054，China) 2(Southwest China Institute of Electronic Technology，Chengdu 610036,China ) Abstract Based on the extension of the Laurent decomposition of continuous phase modulation (CPM) signals into a sum of plus amplitude modulation (PAM) signals, we drive an optimal and a suboptimal method for reduced complexity maximum-likelihood detector of CPM. We construct a quaternary partial response CPM system, and it proves that we can significantly reduce the complexity of the detector, and we also compare the symbol error probabilities of the optimal method and the suboptimal method. Keywords：Continuous Phase Modulation; Laurent Decomposition; maximum-likelihood estimation; Viterbi algorithm. -6-

资料库

论文研究-基于Laurent分解实现多进制CPM信号的相干检测 .pdf

相关推荐

开发技术

热门标签

最新资料