微环谐振器.pdf-资料库

第 3 章微环谐振器近年来，微环谐振器(Micro-Ring Resonator，MRR)已引起国内外研究者的高度重视和极大兴趣，成为热点研究课题。MRR具有成本低、结构紧凑、集成度高、插入损耗小、串扰低等优点，在光信号处理、滤波、波分复用、解复用、路由、波长变换、调制、开关、激光等方面都具有广泛的应用。由于MRR的谐振不需要腔面或光栅来提供光反馈，因此十分有利于与其他光电子元器件的单片集成。不同半径的微环进行串联，可以有效地增大自由光谱区(FSR)，从而可以有效地增大信道数量。多个微环进行串联和并联，可以形成近于方形的谐振光谱，使得光谱响应变得十分平坦。因而这种MRR阵列可以成为密集型波分复用的理想器件。当前国际上在MRR滤波器方面已做了大量的理论和实验工作，用Si/SiO2、Ta2O5/SiO2、GaAs/AlGaAs、GaInAsP/InP、聚合物等材料制成的器件已有大量的报道，包括单环[21~23]、并联多环[24~27]、串联多环[28~32]、并联串联多环[33-36]等 MRR阵列结构。单环 MRR 的结构最为简单，其他结构复杂的 MRR 阵列都是由多个微环组合而成，单环 MRR 是 MRR 阵列的基本结构，因此对单环 MRR 的特性分析是非常必要的。单环 MRR 有两个基本缺点，一是其光谱响应不平坦，呈上凸形的洛伦兹分布，当器件因工艺误差或因温度变化而引起光谱漂移时，器件不能正常地工作；二是其光谱中的非谐振光较强，这使得单环 MRR 的串扰较大。为了克服单环 MRR 上述两个缺点，可以把多个微环并联或串联起来形成 MRR 阵列，适当选择结构参量，即可获得十分平坦的“箱形”(box-like)光谱响应，又可有效地降低光谱中非谐振光的强度，进而有效地减小器件的串扰。本章将阐述单环MRR[37]和并联多环[38]、串联多环[39]、串联并联多环[40]、并联串联多环[41]等MRR阵列的滤波原理、以及一个分波单元中含有一个微环[42]及含有三个微环 [43]MRR阵列的波分复用原理，给出微环波导和信道波导的截面尺寸、耦合间距、微环半径、相邻微环间的半径差等结构参量的优化方法，并对微环的谐振级数、FSR、微环半径与波长间的色散关系、输出光谱、插入损耗、串扰等特性进行详细地分析模拟。其他类似结构的MRR滤波和波分复用器件的研究内容可参见我们发表的论文[44~49]。这里需要说明的是，MRR 的插入损耗包括模的传输损耗、弯曲损耗、波导界面的散射损耗、由高折射率衬底引起的泄漏损耗等等。通过适当选择微环半径，可使弯曲损耗降至很小以至可以忽略。采用蒸汽回溶技术平滑波导界面可以有效地降低界面的散射 90

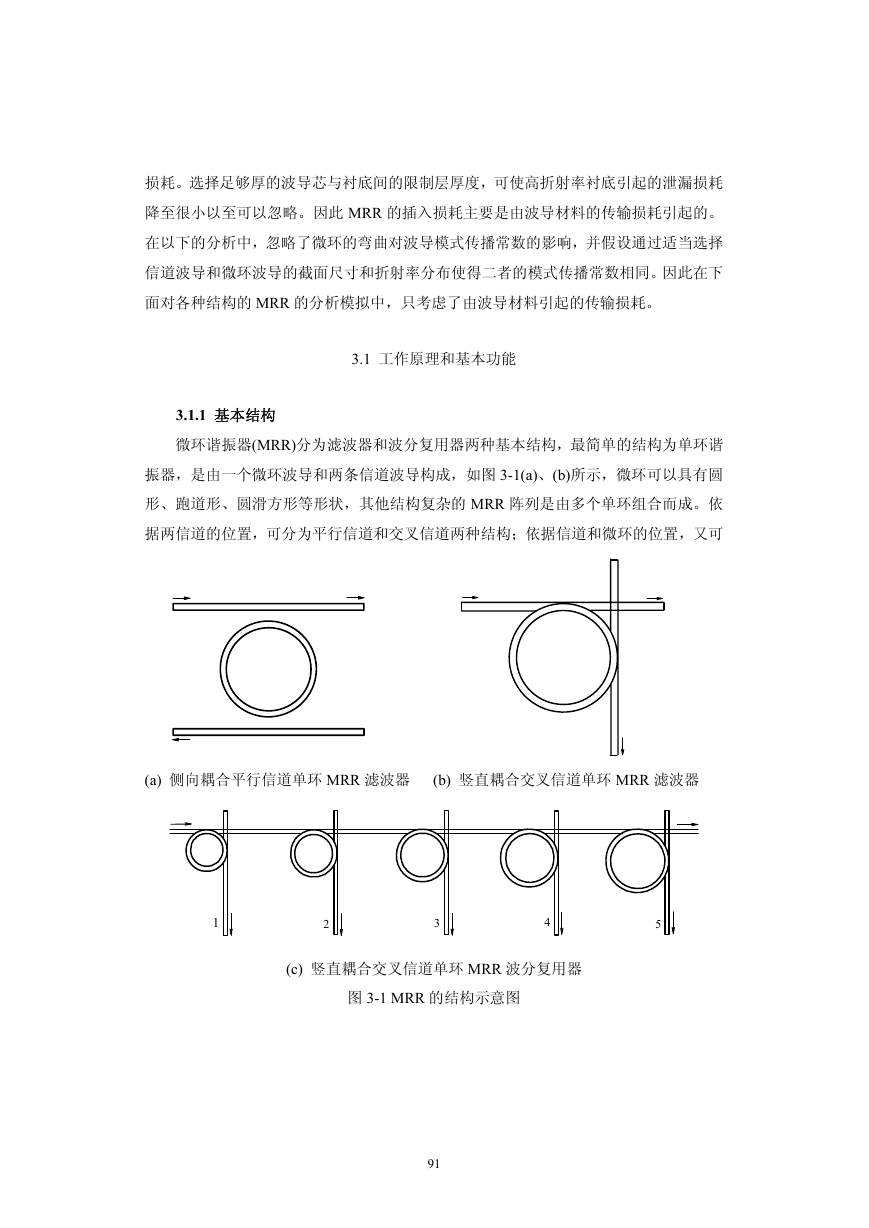
损耗。选择足够厚的波导芯与衬底间的限制层厚度，可使高折射率衬底引起的泄漏损耗降至很小以至可以忽略。因此 MRR 的插入损耗主要是由波导材料的传输损耗引起的。在以下的分析中，忽略了微环的弯曲对波导模式传播常数的影响，并假设通过适当选择信道波导和微环波导的截面尺寸和折射率分布使得二者的模式传播常数相同。因此在下面对各种结构的 MRR 的分析模拟中，只考虑了由波导材料引起的传输损耗。 3.1 工作原理和基本功能 3.1.1 基本结构微环谐振器(MRR)分为滤波器和波分复用器两种基本结构，最简单的结构为单环谐振器，是由一个微环波导和两条信道波导构成，如图 3-1(a)、(b)所示，微环可以具有圆形、跑道形、圆滑方形等形状，其他结构复杂的 MRR 阵列是由多个单环组合而成。依据两信道的位置，可分为平行信道和交叉信道两种结构；依据信道和微环的位置，又可 10 8 6 4 2 0 10 8 6 4 2 0 0 2 4 6 8 10 0 2 4 6 8 10 (a) 侧向耦合平行信道单环 MRR 滤波器 (b) 竖直耦合交叉信道单环 MRR 滤波器 10 8 6 4 2 0 1 0 2 2 4 6 3 8 10 4 5 (c) 竖直耦合交叉信道单环 MRR 波分复用器图 3-1 MRR 的结构示意图 91

分为侧向耦合和竖直耦合两种情况。侧向耦合时，信道和微环处于同一平面内，二者之间存在一宽度为 d 的中心耦合间距；竖直耦合时，微环在信道之上，二者之间存在一厚度为 d 的耦合层。图 3-1(a) 显示了侧向耦合时平行信道单环 MRR 滤波器的结构，而图 3-1(b)显示了竖直耦合时交叉信道单环 MRR 滤波器的结构，而图 3-1(c)则显示了竖直耦合交叉信道单环 MRR 波分复用器的基本结构。以图 3-1(a)为例，光在 MRR 中的传输过程是：当信号光从上信道左端口输入后，在邻近微环时要发生相互耦合，其结果使上信道输入的部分光功率不断地耦合进入微环中，同时微环中的部分光功率也要不断地耦合进入上信道中，并由上信道的右端口输出；耦合进入微环中的光在微环中不停地旋转而发生谐振，并在邻近下信道时也要发生相互耦合，其结果使微环中的部分光功率不断地耦合进入下信道中，并由下信道的左端口输出。 MRR 滤波器只具有滤波功能，而 MRR 波分复用器可具有解复用、复用和周期性三种基本功能，将在下面分别加以说明。 3.1.2 微环谐振方程光在微环中传输时，只有那些绕微环传输一周时所产生的光程差为波长的整数倍的光才能产生谐振而加强，即满足下述的微环谐振方程 2 Rn = π c λm (3.1-1) 或者说，只有那些绕微环传输一周时所产生的相位差为 2π 的整数倍的光才能产生谐振而加强，此时的微环谐振方程为 R 2 β π 2 π= m (3.1-2) 式中，R为微环的谐振半径，nc为微环波导中模有效折射率，β为模传播常数，λ为真空中光波长，m为谐振级数，取正整数。微环的谐振级数m是一个重要参量，一旦谐振级数m确定后，则其它一些参量如微环谐振半径、半径-波长色散方程、相邻微环的半径差、自由光谱区(FSR)等表达式也随之确定，并可由微环谐振方程推导出来。 3.1.3 微环谐振半径由式(3.1-1)得到微环的谐振半径 R 为 R = m λ (3.1-3) 2 n π c 3.1.4 半径-波长色散方程 92

某一波长的信号光在微环中谐振时必须满足微环谐振方程(3.1-1)，不同波长的光所对应的模有效折射率nc互不相同，谐振时所对应的微环半径R也互不相同，因此可以把，而把R 看成是谐振级数m 和波长λ的函数， nc 看成是波长λ的函数， )λ,mRR = Rn ∂ π ∂ λ (3.1-4) 。式(3.1-1)对波长λ求偏导，可得 n d c d λ R 2 + π ( )λc n = c m = n ( 2 c 由此得到 = R ∂ λ ∂ R m 21 π ⎛ −⎜ m n π ⎝ c ⎞ ⎟ (3.1-5) ⎠ 利用式(3.1-1)，式(3.1-5)变为 n d c d λ 2 R ∂ λ ∂ = m n ⎛ ⎜ n 2 π ⎝ c c 2 − n d c λ d λ ⎞ ⎟ (3.1-6) ⎠ 由此得到 MRR 的半径-波长色散方程为 R ∂ λ ∂ = mn g 2 2 n π c (3.1-7) 式中ng为波导的群折射率，定义为 n g = n c − λ n d c d λ (3.1-8) 3.1.5 相邻微环半径差 mΔ 令谐振级数改变、谐振波长改变Δλ时，微环谐振半径改变为 ΔR ，由于 ( ，由式(3.1-3)、(3.1-7)可得 )λ,mRR = =Δ R R ∂ m ∂ +Δ m R ∂ ∂ λ =Δ λ 1 n π c 2 ⎛ ⎜⎜ ⎝ λ +Δ m g mn n c ⎞ ⎟⎟ Δ λ ⎠ (3.1-9) 式中 mΔ = 0, 1, 2, L 。式(3.1-9)说明，ΔR 与Δm 或Δλ呈线性关系，即当微环谐振级数每改变Δm、同时信号光的谐振波长每改变Δλ时，则要求微环的谐振半径改变ΔR，即等间隔波长的信号光从输入信道输入后，将分别耦合进入具有等间隔半径的不同微环中发生谐振，然后耦合进入相应的输出信道中输出，从而实现解复用功能，参见图 3.1(c)。 Δλ称为波长间隔，ΔR 称为相邻微环半径差。 3.1.6 FSR 光谱中两个相邻的谐振峰之间的波长差称为 FSR。令这两个谐振峰所对应的谐振级 93

应的谐振级数差数分别为 m 和 1−m ，由式(3.1-1)可以看出，m 减小时，波长增大，因此一个 FSR 所对。当某一波长为λ的信号光在半径为 R 的微环中谐振时，必须 ( )λc 满足微环谐振方程(3.1-1)。此时 R 保持定值， 1−=Δm 1−=Δm ，由于 n = c FSR Δ mλ ， = n ，式(3.1-1)对波长λ求微分，可得 2 nR cd π d λ 于是得到 λ Δ m m = Δ λ λ + Δ m m Δ= mm λλ − (3.1-10) = Δλ m FSR nR cd 2 π ⎤ ⎥ m d λ ⎦ 利用式(3.1-1)，式(3.1-11)变为 ⎡ 1 −⎢⎣ λ m = 1 − (3.1-11) FSR = 1 − n λ c m ⎡ n −⎢⎣ c n d c ⎤ λ ⎥ d λ ⎦ (3.1-12) 利用式(3.1-8)，可得到 FSR 为 FSR = nλ mn c g (3.1-13) 3.1.7 输出信道波导数不同波长的信号光，可能从相同的端口输出，FSR也就是这样的波长间隔范围，所以FSR决定了最大可能的输出信道波导数Nmax，为 N max = int FSR Δ λ ⎛ ⎜ ⎝ ⎞ =⎟ ⎠ int ⎛ ⎜ ⎜ ⎝ ⎞ n λ ⎟ c ⎟ mn Δ λ ⎠ g (3.1-14) 3.1.8 基本功能 1. MRR 滤波器如图 3-1(a)、(b)所示，含有不同波长的复信号光从上信道输入端口输入并耦合进入微环后，其中只有某一特定波长的光能满足谐振条件而在微环中引起谐振，耦合进入下信道或竖直信道的光以这一谐振波长的输出光强为最大，从而完成了滤波功能。 2. MRR 波分复用器我们在上信道输入端口输入 N 个波长的信号光，令相邻波长的信号光的波长差为 Δλ，则第 i 个波长为 λλ i 1 = ( i Δ−+ ) λ 1 ( i = ,2,1 , L )N ， 1λ为初始波长。 (1) 解复用 94

如图 3-1(c)所示，含有不同波长的复信号光从上信道输入端口输入并耦合进入不同半径的微环后，每个微环中只有一个波长的光能满足谐振条件而引起谐振，不同半径的微环中谐振光的波长也互不相同，因而耦合进入不同的竖直信道后具有最大输出光强的光的波长也互不相同，从而完成了解复用功能。 (2) 复用反之，从不同的竖直信道端口输入不同波长的信号光耦合进入不同半径的微环谐振后，再耦合进入上信道后的输出光为这些波长的复合光，从而完成了复用功能。 (3) 周期性对于 FSR λΔ= N 的器件，波长为λi和λi+N ( FSR λλ =+ + Ni i λΔ≠ N FSR = Ni λ Δ+ )λ 的信号光将的器件则无周期性。如图 3-1(c) 从同一端口输出，这种性质称为周期性。对于所示，此时N = 5，令从上信道输入的λ1，λ2，λ3，λ4，λ5五个波长的信号光分别从第 1， 2，3，4，5 条竖直信道输出。如果输入的信号光为λ0，λ1，λ2，λ3，λ4，λ5六个波长，其中波长为λ1，λ2，λ3，λ4的信号光仍分别从第 1，2，3，4 条竖直信道输出，对于波长为λ0和λ5的两个信号光，根据周期性， λλ 0 =+ 50 5 Δ+ λ ，即有 λλ 5 0 = 5 Δ+ λ ，则波长为 λ0和λ5的两个信号光都能从第 5 个端口输出。如果输入波长中没有λ0，则从第 5 个端口输出的只是波长为λ5的信号光。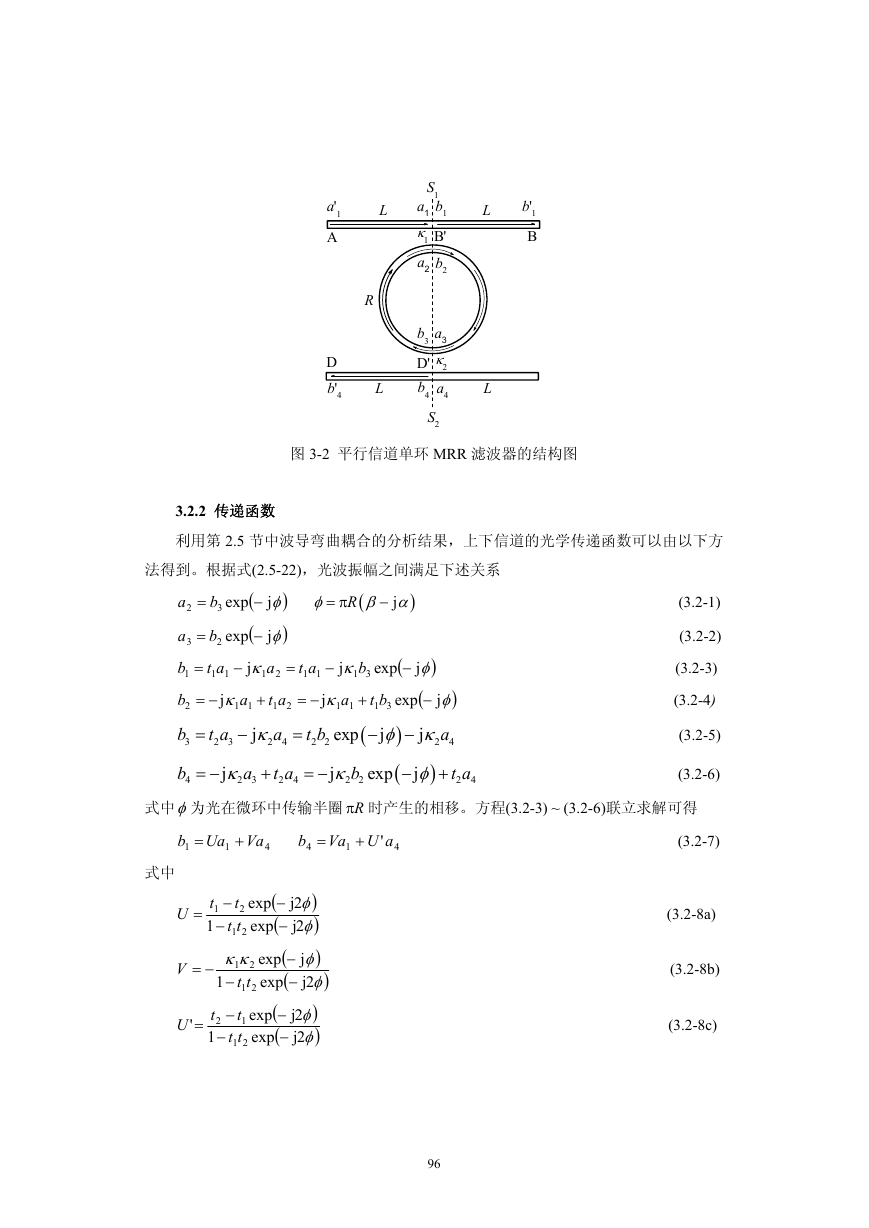 3.2 平行信道单环 MRR 滤波器 3.2.1 器件结构平行信道单环MRR滤波器的结构如图 3-2 所示，它是由两条平行信道和一个微环构成。令微环半径为R，两条平行信道的长度相等，各为 2L，L为信道端口到耦合点的距离。令微环波导和信道波导的模式传播常数相等皆为β，并令α为微环及信道中模式的损耗系数，相应的模复传播常数为 jβ α− 。令微环与上信道间、微环与下信道间的振幅耦合比率分别为 1κ 、 2κ ，相应的振幅透射比率为t1、t2。通过微环的圆心和信道与微环间的耦合点作截面S1、S2，令在信道和微环中光波通过上述截面的输入和输出振幅分别为ai、bi。 95

a'1 A D b'4 L R 0 L 2 10 S1 a1 b1 κ1 B' a2 b2 a3 b3 κ2D' b4 a4 S2 4 6 8 6 4 2 0 L b'1 B 8 10 L 图 3-2 平行信道单环 MRR 滤波器的结构图 3.2.2 传递函数利用第 2.5 节中波导弯曲耦合的分析结果，上下信道的光学传递函数可以由以下方法得到。根据式(2.5-22)，光波振幅之间满足下述关系 a 2 = b 3 exp Rφ = π ( ) β α − j (3.2-1) exp = b 2 at 11 j κ −= = − = t a 2 3 + a 11 j κ − ( − ( − j κ )φj )φj a = 21 at 21 a 2 4 t a 2 4 + 3 a b 1 b 2 b 3 b 4 = − j κ a 2 3 = − j κ b 2 2 (3.2-2) at 11 − j κ b 31 −= j κ = t b 2 2 a 11 exp + ( exp )φ j ( − j ( − bt exp 31 ) j φ κ 2 ) ( j − φ exp − − (3.2-4) (3.2-3) )φ j a4 t 4a (3.2-6) (3.2-5) + 2 式中φ为光在微环中传输半圈 Rπ 时产生的相移。方程(3.2-3) ~ (3.2-6)联立求解可得 b 1 = Ua 1 + Va 4 b 4 = Va 1 + 'aU 4 (3.2-7) 式中 t tU − 2 1 = tt 1 − 21 ( exp − ( exp − ( exp − κκ 21 ( tt exp 1 − − 21 ( t exp − − 1 ( tt exp − 21 ) 2j φ )φ 2j ) j φ )φ 2j ) 2j φ )φ 2j 2 − V −= tU ' = 1 (3.2-8a) (3.2-8b) (3.2-8c) 96

注意此时 4 =a 0 ，代入式(3.2-7)得到 b 1 a 1 = U b 4 a 1 = V (3.2-9) 在上信道的输入/输出端口处光波的输入/输出振幅及在下信道的输出端口处光波的输出振幅分别为 ( )ψj exp ( exp − 1 a a = ' 1 = b 4 b 4 ' )ψj = b 1 )ψj b ' 1 ) Lψ β α exp ( ( − − = j (3.2-10) (3.2-11) 式中ψ为光在信道中传输路程 L 时产生的相移。利用式(3.2-9)~(3.2-11)，则可得到由上信道输入端口至其输出端口的振幅传递函数 B 和由上信道输入端口至下信道输出端口的振幅传递函数 D 分别为 bB ' 1 = a ' 1 bD ' 4 = a ' 1 = = b 1 a 1 b 4 a 1 exp ( − )ψ2j = U ( exp − )ψ2j (3.2-12) exp ( − ) 2j ψ = V exp ( ψ − 2j ) (3.2-13) 由此得到相应的光强传递函数|B|2、|D|2分别为 2 B = U 2 D = V 2j ) 2 exp ψ− ) 2 exp ψ− ( ( 2j (3.2-14) (3.2-15) 式(3.2-8)代入式(3.2-14)、(3.2-15)，可以得到 2B 、 2D 的明显表达式为 2 B = [ t 1 − t ( exp − 2 tt 1 − 21 ] ( ) 2j exp φ − ( ) exp 2j − φ 2 ) 2j ψ (3.2-16) 2 D = κκ 21 1 − [ ] ( ) exp 2 j ψφ − + ( ) tt 2j exp φ − 21 2 (3.2-17) 可以证明在无损耗的情况下，即令 0α= ，利用微环谐振方程(3.1-1)，由式(3.2-16)、(3.2-17) 可得 2 B + D 12 = (3.2-18) 式(3.2-18)说明在无损耗的情况下，器件的总输入输出功率守恒。特别是当 2κ κ= 1 0α= 、 2 B = 及 0 时，在谐振状态下，利用微环谐振方程(3.1-1)，由式(3.2-17)可以得到 97 2 D = ， 1

资料库

微环谐振器.pdf

相关推荐

课程资源

热门标签

最新资料