Verhulst反函数模型滑坡起始预测时刻的选择.pdf-资料库

第 27 卷增 1 岩石力学与工程学报 Vol.27 Supp.1 2008 年 6 月 Chinese Journal of Rock Mechanics and Engineering June，2008 Verhulst 反函数模型滑坡起始预测时刻的选择龙万学 1，林剑 2，许湘华 1，廖秀英 2，彭小平 1 (1. 贵州省交通规划勘察设计研究院，贵州贵阳 550001；2. 湖南科技大学建筑学院，湖南湘潭 411201) 摘要：Verhulst 反函数模型用于滑坡预测的关键在于起始预测时刻 t0 的选择。针对用定量计算方法选择 t0，研究模型中对数函数自变量存在出现负值的问题。计算所有 t0 满足模型要求的累计位移和相对位移预测数据，形成预测曲线，通过分析预测曲线与实际监测曲线选择起始预测时刻 t0 值，得出其选择的主要原则：(1) 预测位移在观测序列点 n 和 n +1 处成立；(2) 预测累计位移曲线与实测曲线形态相似；(3) 预测相对位移与实测相对位移在点 n 处差值最小。多种已知滑坡试验表明：其临滑时刻的预测精度可以达到 1 个时间间隔以内，t0 选择方法是有效的。关键词：边坡工程；滑坡预测；临滑时刻；Verhulst 反函数模型；起始预测时刻中图分类号：P 644.22 文献标识码：A 文章编号：1000–6915(2008)增 1–3298–07 SELECTION OF INITIAL PREDICTION TIME FOR LANDSLIDE WITH VERHULST INVERSE FUNCTION MODEL LONG Wanxue1，LIN Jian2，XU Xianghua1，LIAO Xiuying2，PENG Xiaoping1 (1. Guizhou Provincial Institute of Planning，Prospecting and Designing of Communications Infrastructures，Guiyang， Guizhou 550001，China；2. School of Architecture and Urban Planning，Hunan University of Science and Technology， Xiangtan，Hunan 411201，China) 0t ，and all predicted Abstract：It is a key problem to select the initial prediction time 0t with Verhulst inverse function model in 0t by quantitative calculation method in that the landslide study. Generally，there is a problem of selecting independent variable of logarithm function in the model may be negative. The predicted data of accumulated 0t -curves are formed. The displacement and relative displacement are calculated with all 0t can be selected with analyzing the predicted curves and monitoring curves. The selecting initial prediction time principles are as follows：(1) the predicted displacements can be calculated on points n and n+1 of the monitoring list；(2) the curve configuration of predicted accumulated displacements is similar to the monitoring curve；and (3) the dispersion between the monitoring relative displacement and its predicted value on the point n is the least. The experimental results of several groups of measured data show that the precision of critical sliding time can be obtained within one time interval；and the method to choose Key words：slope engineering；landslide prediction；critical sliding time；Verhulst inverse function model；initial prediction time 收稿日期：2008–02–01；修回日期：2008–05–28 基金项目：交通部“西部地区公路地质灾害监测预报技术研究”资助项目(2003–318–802–01) 作者简介：龙万学(1971–)，男，1993 年毕业于南京工业大学岩土工程专业，现任高级工程师，主要从事岩土工程勘察、设计、咨询及地质灾害防治方面的工作。E-mail：lwx2005@gzjtsj.com.cn 0t is effective.

第 27 卷增 1 龙万学，等. Verhulst 反函数模型滑坡起始预测时刻的选择 • 3299 • 1 引言 X ，， (1) t {)( = n )}( X ， )2( )1( X X )0( )0( )0( )0( 对 X )1( X t )()0( X t {)( = 作累加变换得 X )1( ，， X ， )2( )1( )1( )1( n )}( (2a) 其中， X )1( i )( = i ∑ k 1 = X )0( k )( i ( = ，，， n 2 1 ) (2b) 对 tX )()1( 拟合 Verhulst 一阶白化非线性微分方程： t )( X d )1( t d = X a )1( t )( − b [ X )1( t ( )] 2 (3) 式中： a ， b 均为待定系数。式(3)的解为 ˆ X )1( t )( = 1 + a Xb ⎛ ⎜⎜ ⎝ ba / 1 )0( )1( − (4) − ta ( − t ) 0 ⎞ e1 ⎟⎟ ⎠ ˆ X )1( t )( 求的反函数，并进行变量互换，得到 Verhulst 反函数预测模型： t bt ) 0 tbt ) ln1 a − − a a t )( ˆ X ( ( = )1( 0 + X )0( )1( (5) 式中：t 为时间序数， 0t 为起始预测时刻。根据最小二乘法原理，式(5)中的参数 a，b 可由下式求得 a = b = tn 1 −+ 0 ∑ tk = kd )( + b 0 n 0 tn 1 −+ k ∑ tk = 0 tn 1 −+ 0 ∑ tk = kkd ))(( − 0 ⎛ ⎜ ⎜ ⎝ 0 tn 1 −+ k ∑ tk = 0 ⎞ ⎟ ⎟ ⎠ tn 1 −+ 0 ∑ tk = 0 ⎛ ⎜ ⎜ ⎝ 2 kd )( 0 tn 1 −+ k ∑ tk = 0 n − 2 0 tn 1 −+ k ∑ tk = 0 kd /[1)( = X )0( ( k +− t 0 k ])1 n ⎞ ⎟ ⎟ ⎠ ⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎬ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎭ (6) 起始预测时刻 0t 的取值与建模有关，不能简单地取为 0 或 1。通常采用计算机优化的方法搜寻最优解，使得系统输出的平均相对误差 E 满足一定的精度要求，即 E = 1 n n ∑ i 1 = X )0( i )( ˆ X − X )0( t ( )0( i )( 0 ⎛ ⎜ ⎜ ⎝ −+ i )1 ⎞ ⎟ ⎟ ⎠ ≤m (7) Verhulst 模型是德国生物学家Verhulst 建立的用于生物繁殖量随时间发展变化的预测模型[1～3]，现已应用于滑坡预测[4～7]。Verhulst 模型的量化特征曲线呈“S”形，而滑坡变形破坏的相对位移–时间曲线常呈反“S”形，这恰与 Verhulst 模型曲线互为反函数(见图 1)。从量化信息的角度考虑，用 Verhulst 模型的反函数来拟合滑坡的变形特征，建模依据更加充分[8～10]。图1 Verhulst预测模型及其反函数特征曲线 Fig.1 Verhulst prediction model and inverse Verhulst function characteristic curve 但是，Verhulst 反函数模型属于对数模型，对预测数据的要求和模型参数的选择十分严格，H. T. Banks 等[11，12]在研究指数、对数反函数模型对计算数据的敏感性问题时，特别指出了参数选择导致 Verhulst 反函数模型计算错误的问题。Verhulst 反函数模型用于滑坡尚处于典型滑坡的简单计算阶段，缺乏模型对数据的适用性及参数选取准则等基本问题的进一步研究，李天斌和陈明东[13]利用 Verhulst 反函数模型对新滩和陇西滑坡进行预测验证；徐林生[14]用 Verhulst 函数及其反函数模型对公路隧道软弱围岩失稳时刻的预报进行对比计算研究。起始预测时刻 0t 的选择是 Verhulst 反函数模型用于滑坡预测的关键之一，本文利用多组实测滑坡位移数据，通过对不同的初始预测时刻 0t 的 Verhulst 反函数预测曲线进行分析，提出一种初始预测时刻 0t 的选择方法。 2 Verhulst 反函数模型设原始等间隔位移监测数据序列 X t )()0( 为式中：m 为给定的精度。

• 3300 • 岩石力学与工程学报 2008 年计算Verhulst 反函数模型的还原值序列 { X )0( t )}( ：自变量为正，因此，存在式(7)无解的情况。 X )0( t ( + X )1( X X 0 ( )1( t ( )1 = )1 → t )( ln a − t )()1( tbt 0) −+ → +∞ 时，由式(5)可知，当 (8) a ( − a ( − 0 ≠t →0。初始时间序数 0 t bt ) 0 tbt ) ，一般 +∞ ，即 0t ≥0，那么 t→ ba / 。由此可知，滑坡变形量趋于无穷大时，时间 t 趋于一定值 ba / 。因此，可将 T 作为滑坡失稳破坏时的预报时间。这样，从建模数据起始点至滑坡失稳破坏时的预报时间 T ，T 实际上是一个滑坡失稳时间的时为序数，真正的滑坡破坏时间T ′ 为 tba / − ba /= T = 0 T tT ∆=′ (9) 式中： t∆ 为监测数据间隔时间。 3 起始预测时刻 t0 的选择方法 3.1 方法的基本思想及试验数据通常起始预测时刻 0t 是根据给定预测精度 m，由式(7)采用计算机优化的方法搜寻最优解确定的，式(7)中预测相对位移序列最终由反函数模型式(5)确定，而式(5)中的模型待定系数又与 0t 有关，在搜寻最优解的过程中所选取 0t 值，不能确保时间序数[1，n]的范围内使式(5)中对数函数的 + t )1 ˆ X i ( − )0( 0 本文选择起始预测时刻 0t 的基本思想是：计算所有 0t 能满足对数函数自变量大于 0 的预测相对位移序列和预测累计位移序列，通过与实际序列对比确定最佳的起始预测时刻 0t ，其试验数据如表 1 所示。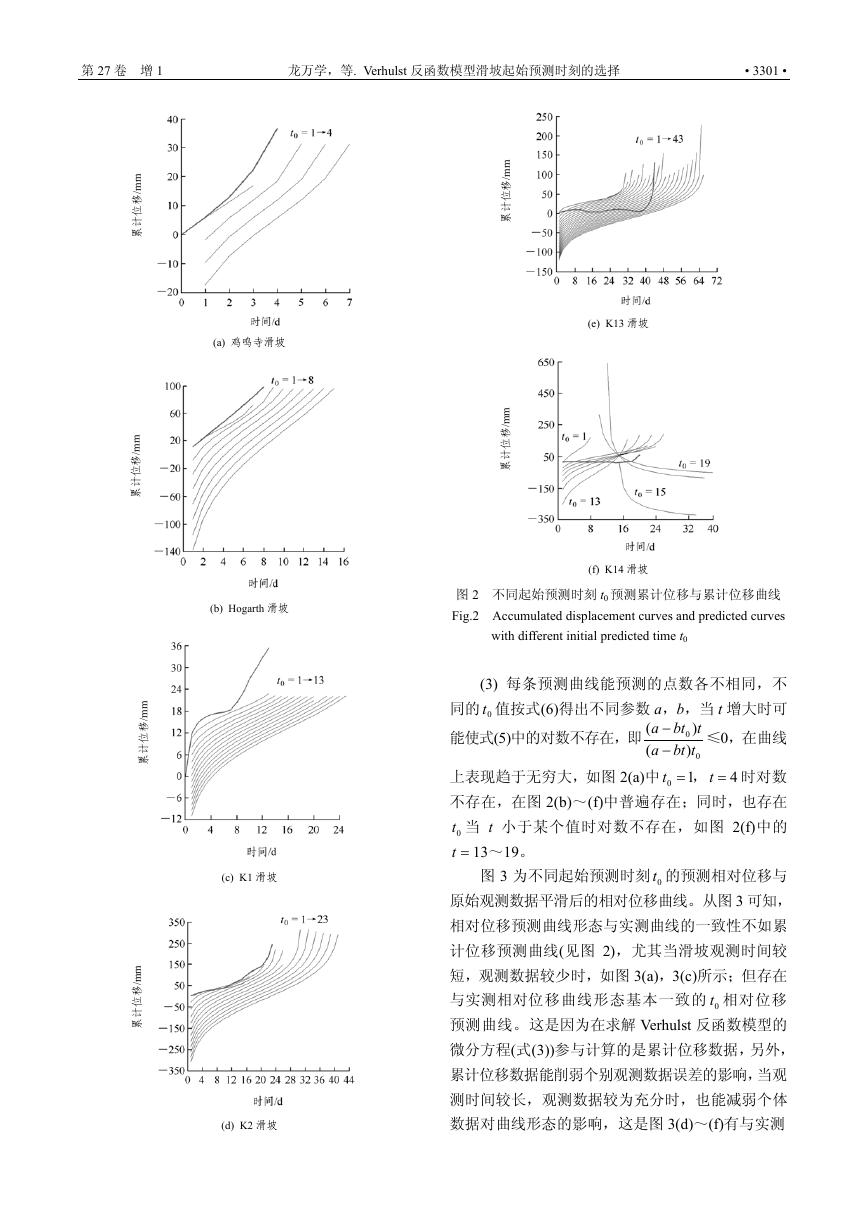 3.2 不同起始预测时刻 t0 的预测曲线特征原始数据采用五点三次平滑，非等间距进行线性插值处理，插值间隔为平均观测时刻的 1/2 左右， K2，K13 和 K14(滑坡名)观测时间序列的插值时间间隔分别为 11，5 和 10 d。图 2 为采用不同起始预测时刻 0t 的预测累计位移和插值平滑后的累计位移曲线，横坐标为观测时刻序列，表示观测时刻距起始观测时刻的单位时间间隔，其中图 2(a)～(c)中的 0t 分别为第一个至最后一个观测时刻的完全选择，图 2(d)～(f)间隔选择，计算自第一个至最后观测时，，，刻加 0t 个时间间隔的预测值，即 2 1 l ( 0 − 从图 2 中可见： (1) 预测曲线均为 Verhulst 反函数曲线，当观测数据存在较长的平稳期，其预测曲线为完整的反函数曲线，如图 2(d)，(e)所示。，l 为观测序列的时间间隔数)。 (ˆ =nnX + t )1 )( (2) 不同的 0t 为一系列的反函数平移曲线，当观测累计位移数据为单调增时，预测曲线多处于累计位移曲线下方。表 1 滑坡监测时间序列表 Table 1 Time list of landslide monitoring 鸡鸣寺滑坡 (1991 年，等间隔 24 h) 加拿大 Hogarth 滑坡 (1975 年，等间隔 15 d) 贵州模拟试验 K1 滑坡 (2005 年，等间隔 6 h) 贵州永宁 K2 滑坡 (2006 年，非等距) 贵州晴隆 K13 滑坡 (2005 年，非等距) 贵州晴隆 K14 滑坡 (2005 年，非等距) 时间位移/mm 时间位移/mm 时间位移/mm 时间位移/mm 时间位移/mm 时间位移/mm 6 月 25 日 10:00 6.0 1 月 15 日 11.60 4 月 17 日 10:00 11.71 9 月 20 日 8.93 11 月 9 日 1.30 11 月 26 日 17.64 6 月 26 日 10:00 7.0 1 月 30 日 11.72 4 月 17 日 16:00 15.25 10 月 20 日 10.99 11 月 30 日 6 月 27 日 10:00 9.4 2 月 14 日 11.65 4 月 17 日 02:00 14.87 12 月 22 日 27.57 12 月 13 日 7.54 1.20 12 月 2 日－1.35 1 月 10 日 1.86 6 月 28 日 10:00 14.3 3 月 1 日 11.70 4 月 18 日 04:00 18.23 1 月 5 日 2.79 12 月 31 日－1.35 2 月 21 日－5.70 3 月 16 日 11.90 4 月 18 日 10:00 17.18 2 月 8 日 26.30 1 月 8 日 0.29 3 月 31 日 3 月 31 日 12.10 4 月 18 日 16:00 16.93 3 月 9 日 45.92 1 月 13 日－4.48 4 月 8 日 0.37 6.67 4 月 15 日 12.60 4 月 18 日 22:00 19.61 4 月 11 日 25.37 2 月 17 日－2.14 5 月 22 日－2.95 4 月 30 日 13.90 4 月 19 日 04:00 18.83 4 月 29 日 32.32 2 月 21 日 6.49 6 月 14 日 60.12 4 月 19 日 10:00 23.96 5 月 21 日 117.90 3 月 17 日 1.13 4 月 19 日 16:00 26.64 4 月 19 日 22:00 29.62

第 27 卷增 1 龙万学，等. Verhulst 反函数模型滑坡起始预测时刻的选择 • 3301 • / m m 移位计累 / m m 移位计累 / m m 移位计累 / m m 移位计累 / m m 移位计累 (a) 鸡鸣寺滑坡 (b) Hogarth 滑坡 (c) K1 滑坡 (d) K2 滑坡 (e) K13 滑坡 / m m 移位计累 (f) K14 滑坡图 2 不同起始预测时刻 t0 预测累计位移与累计位移曲线 Fig.2 Accumulated displacement curves and predicted curves with different initial predicted time t0 t bt ) − 0 tbt ) − 0 0 =t ，1 (3) 每条预测曲线能预测的点数各不相同，不同的 0t 值按式(6)得出不同参数 a，b，当 t 增大时可能使式(5)中的对数不存在，即 ≤0，在曲线 a ( a ( 4=t 时对数上表现趋于无穷大，如图 2(a)中不存在，在图 2(b)～(f)中普遍存在；同时，也存在 0t 当 t 小于某个值时对数不存在，如图 2(f)中的 =t 13～19。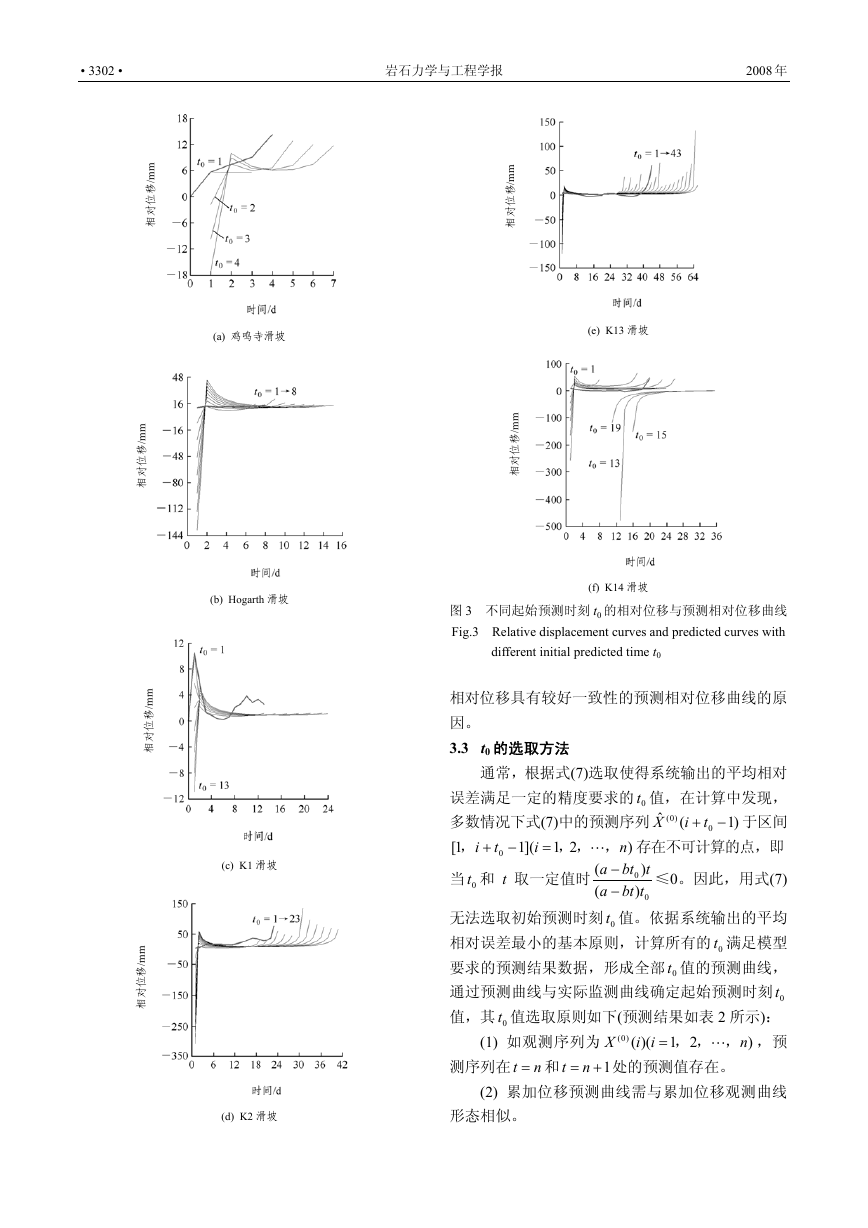图 3 为不同起始预测时刻 0t 的预测相对位移与原始观测数据平滑后的相对位移曲线。从图 3 可知，相对位移预测曲线形态与实测曲线的一致性不如累计位移预测曲线(见图 2)，尤其当滑坡观测时间较短，观测数据较少时，如图 3(a)，3(c)所示；但存在与实测相对位移曲线形态基本一致的 0t 相对位移预测曲线。这是因为在求解 Verhulst 反函数模型的微分方程(式(3))参与计算的是累计位移数据，另外，累计位移数据能削弱个别观测数据误差的影响，当观测时间较长，观测数据较为充分时，也能减弱个体数据对曲线形态的影响，这是图 3(d)～(f)有与实测

• 3302 • 岩石力学与工程学报 2008 年 / m m 移位对相 / m m 移位对相 / m m 移位对相 / m m 移位对相 (a) 鸡鸣寺滑坡 (b) Hogarth 滑坡 (c) K1 滑坡 / m m 移位对相 / m m 移位对相 (e) K13 滑坡 (f) K14 滑坡图 3 不同起始预测时刻 t0 的相对位移与预测相对位移曲线 Fig.3 Relative displacement curves and predicted curves with different initial predicted time t0 相对位移具有较好一致性的预测相对位移曲线的原因。 3.3 t0 的选取方法通常，根据式(7)选取使得系统输出的平均相对误差满足一定的精度要求的 0t 值，在计算中发现，多数情况下式(7)中的预测序列于区间 i 1[ ， i ](1 + t )1 ˆ X i ( − = − + )0( n 2 1 ) 存在不可计算的点，即，，， t bt ) − 0 tbt ) − ≤0。因此，用式(7) a ( a ( 当 0t 和 t 取一定值时 t 0 0 0 无法选取初始预测时刻 0t 值。依据系统输出的平均相对误差最小的基本原则，计算所有的 0t 满足模型要求的预测结果数据，形成全部 0t 值的预测曲线，通过预测曲线与实际监测曲线确定起始预测时刻 0t 值，其 0t 值选取原则如下(预测结果如表 2 所示)：，预 (1) 如观测序列为 ) i ，，， n X i )(()0( 2 1 1+= n 处的预测值存在。 = 测序列在 n t = 和 t (2) 累加位移预测曲线需与累加位移观测曲线 (d) K2 滑坡形态相似。

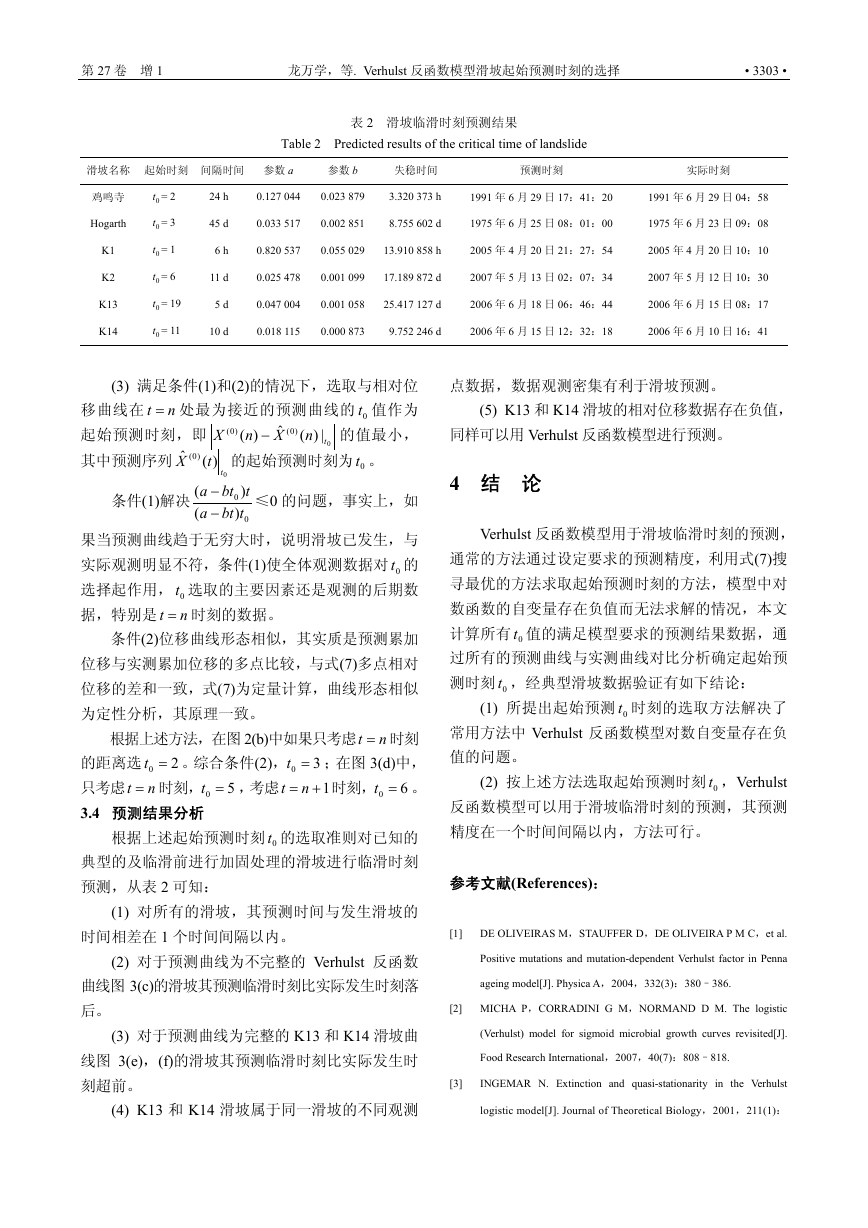
第 27 卷增 1 龙万学，等. Verhulst 反函数模型滑坡起始预测时刻的选择 • 3303 • 表 2 滑坡临滑时刻预测结果 Table 2 Predicted results of the critical time of landslide 滑坡名称起始时刻间隔时间参数 a 参数 b 失稳时间预测时刻实际时刻鸡鸣寺 Hogarth K1 K2 K13 K14 t0 = 2 t0 = 3 t0 = 1 t0 = 6 t0 = 19 t0 = 11 24 h 45 d 6 h 11 d 5 d 10 d 0.127 044 0.023 879 3.320 373 h 1991 年 6 月 29 日 17：41：20 1991 年 6 月 29 日 04：58 0.033 517 0.002 851 8.755 602 d 1975 年 6 月 25 日 08：01：00 1975 年 6 月 23 日 09：08 0.820 537 0.055 029 13.910 858 h 2005 年 4 月 20 日 21：27：54 2005 年 4 月 20 日 10：10 0.025 478 0.001 099 17.189 872 d 2007 年 5 月 13 日 02：07：34 2007 年 5 月 12 日 10：30 0.047 004 0.001 058 25.417 127 d 2006 年 6 月 18 日 06：46：44 2006 年 6 月 15 日 08：17 0.018 115 0.000 873 9.752 246 d 2006 年 6 月 15 日 12：32：18 2006 年 6 月 10 日 16：41 (3) 满足条件(1)和(2)的情况下，选取与相对位 t = 处最为接近的预测曲线的 0t 值作为的值最小， ˆ X )0( 移曲线在 n X 起始预测时刻，即 t )( )0( 其中预测序列 ˆ X )0( − tn 0|)( n )( 的起始预测时刻为 0t 。 t bt t ) 0 tbt ) 0 ≤0 的问题，事实上，如 0 条件(1)解决 ( ( a a − − 果当预测曲线趋于无穷大时，说明滑坡已发生，与实际观测明显不符，条件(1)使全体观测数据对 0t 的选择起作用， 0t 选取的主要因素还是观测的后期数据，特别是 n t = 时刻的数据。条件(2)位移曲线形态相似，其实质是预测累加位移与实测累加位移的多点比较，与式(7)多点相对位移的差和一致，式(7)为定量计算，曲线形态相似为定性分析，其原理一致。根据上述方法，在图 2(b)中如果只考虑 n t = 时刻；在图 3(d)中， 0 =t 。时刻， 6 0 =t 的距离选 2 只考虑 n 3.4 预测结果分析 0 =t t = 时刻， 5 0 =t 。综合条件(2)， 3 1+= n ，考虑 t 根据上述起始预测时刻 0t 的选取准则对已知的典型的及临滑前进行加固处理的滑坡进行临滑时刻预测，从表 2 可知： (1) 对所有的滑坡，其预测时间与发生滑坡的时间相差在 1 个时间间隔以内。 (2) 对于预测曲线为不完整的 Verhulst 反函数曲线图 3(c)的滑坡其预测临滑时刻比实际发生时刻落后。 (3) 对于预测曲线为完整的 K13 和 K14 滑坡曲线图 3(e)，(f)的滑坡其预测临滑时刻比实际发生时刻超前。 (4) K13 和 K14 滑坡属于同一滑坡的不同观测点数据，数据观测密集有利于滑坡预测。 (5) K13 和 K14 滑坡的相对位移数据存在负值，同样可以用 Verhulst 反函数模型进行预测。 4 结论 Verhulst 反函数模型用于滑坡临滑时刻的预测，通常的方法通过设定要求的预测精度，利用式(7)搜寻最优的方法求取起始预测时刻的方法，模型中对数函数的自变量存在负值而无法求解的情况，本文计算所有 0t 值的满足模型要求的预测结果数据，通过所有的预测曲线与实测曲线对比分析确定起始预测时刻 0t ，经典型滑坡数据验证有如下结论： (1) 所提出起始预测 0t 时刻的选取方法解决了常用方法中 Verhulst 反函数模型对数自变量存在负值的问题。 (2) 按上述方法选取起始预测时刻 0t ，Verhulst 反函数模型可以用于滑坡临滑时刻的预测，其预测精度在一个时间间隔以内，方法可行。参考文献(References)： [1] DE OLIVEIRAS M，STAUFFER D，DE OLIVEIRA P M C，et al. Positive mutations and mutation-dependent Verhulst factor in Penna ageing model[J]. Physica A，2004，332(3)：380–386. [2] MICHA P，CORRADINI G M，NORMAND D M. The logistic (Verhulst) model for sigmoid microbial growth curves revisited[J]. Food Research International，2007，40(7)：808–818. [3] INGEMAR N. Extinction and quasi-stationarity in the Verhulst logistic model[J]. Journal of Theoretical Biology，2001，211(1)：

• 3304 • 岩石力学与工程学报 2008 年 11–27. [9] HSU L C，CHEN C Y. Applications of improved grey prediction [4] 殷坤龙，晏同珍. 滑坡预测及相关模型[J]. 岩石力学与工程学报， model for power demand forecasting[J]. Energy Conversion and 1996 ，15(1) ：1 –8.(YIN Kunlong ，YAN Tongzhen. Landslide Management，2003，44(14)：2 241–2 249. prediction and relevant models[J]. Chinese Journal of Rock Mechanics [10] SWART J H，MURRELL H C. A generalised Verhulst model of a and Engineering，1996，15(1)：1–8.(in Chinese)) population subject to seasonal change in both carrying capacity and [5] 唐天国，万星，刘浩吾. 高边坡安全监测的改进 GM 模型预测 growth rate[J]. Chaos，Solitons and Fractals，2007，314(2/3)：研究[J]. 岩石力学与工程学报，2005，24(2)：307–312.(TANG 568–572. Tianguo，WAN Xing，LIU Haowu. Improved GM model for safety [11] BANKS H T，DEDIU S，ERNSTBERGER S L. Sensitivity functions monitoring of high rock slopes[J]. Chinese Journal of Rock Mechanics and their uses in inverse problems[J]. Journal of Inverse and Ill-posed and Engineering，2005，24(2)：307–312.(in Chinese)) Problems，2007，15(7)：683–708. [6] 谢锋，朱陆明，王立忠. 滑坡监控信息分析中的修正灰色系统 [12] SHIH S D. Comments on“A new method for the explicit integration 预测模型及应用[J]. 岩石力学与工程学报，2005，24(22)：4 099– of Lotka-Volterra equations”[J]. Divulgaciones Atemáticas，2005， 4 105.(XIE Feng，ZHU Luming，WANG Lizhong. Modified grey 13(2)：99–106. system forecasting model and its application to analyzing information [13] 李天斌，陈明东. 滑坡时间预报的费尔哈斯反函数法[J]. 地质灾害 of landslide monitory[J]. Chinese Journal of Rock Mechanics and 与环境保护，1996，7(3)：13–17.(LI Tianbin，CHEN Mingdong. Engineering，2005，24(22)：4 099–4 105.(in Chinese)) Time prediction of landslide using Verhulst inverse function model[J]. [7] 蒋刚，林鲁生，刘祖德，等. 边坡变形的灰色预测模型[J]. 岩土 Journal of Geological Hazards and Environment Preservation，1996，力学，2000，21(3)：243–246.(JIANG Gang，LIN Lusheng，LIU 7(3)：13–17.(in Chinese)) Zude，et al. Prediction grey model for slope displacement[J]. Rock [14] 徐林生. 公路隧道围岩稳定位移与突发失稳时间预报研究[J]. 重 and Soil Mechanics，2000，21(3)：243–246.(in Chinese)) 庆交通学院学报，2005，24(5)：18–24.(XU Linsheng. Research on [8] 邓聚龙. 灰预测与灰决策[M]. 武汉：华中科技大学出版社，2002. prediction of stable displacement and unstable time on highway (DENG Julong. Grey forecasting and decision[M]. Wuhan：Huazhong tunnel[J]. Journal of Chongqing Jiaotong University，2005，24(5)： University of Science and Technology Press，2002.(in Chinese)) 18–24.(in Chinese))

资料库

Verhulst反函数模型滑坡起始预测时刻的选择.pdf

相关推荐

课程资源

热门标签

最新资料