第1页 / 共7页
第2页 / 共7页
第3页 / 共7页
第4页 / 共7页
第5页 / 共7页
第6页 / 共7页
第7页 / 共7页
卷积神经网络的数学推导.pdf
神经网络
前向传导
输入层
隐藏层
输出层
前向传导
反向传播
卷积神经网络
卷积
池化
卷积神经网络
前向传导
反向传播
卷积神经网络的数学推导
Author: idiomer
Typesetting: Cater Wu
2016 年 8 月 10 日
目录
1 神经网络
1.1 前向传导 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.1.1 输入层 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.1.2 隐藏层 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.1.3 输出层 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.1.4 前向传导 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.2 反向传播 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2 卷积神经网络
2.1 卷积 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.2 池化 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.3 卷积神经网络 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.3.1 前向传导 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.3.2 反向传播 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1
2
2
2
2
3
3
4
4
4
5
5
6
导言
卷积神经网络（Convolutional Neural Network, CNN）是一种前馈神经网络，每个神经元都只
影响邻层的一部分神经元，具有局部感受野，因此，网络具有极强的捕捉局部特征的能力；另一方
面，通过权值共享和池化，显著地降低了网络的计算复杂度，使得 CNN 得到广泛应用。CNN 是图
像分类和语音识别领域的杰出算法，也是目前大部分计算机视觉系统的核心技术，从 facebook 的图
像自动标签到自动驾驶汽车，乃至 AlphaGo 都在使用。与此同时，近两年 CNN 逐渐被应用于 NLP
任务，在 sentence classification 中，基于 CNN 的模型取得了非常显著的效果。
本文假设读者比较熟悉神经网络的相关知识，特别是反向传播算法的过程，从数学推导的角度
来理解 CNN 的内部原理。
1 神经网络
神经网络是由多个感知器（神经元）构成的全连接的网络，本质上来说，这样的连接只是简单
的线性加权和而已，所以每个神经元加上同一个非线性函数（如 sigmoidtanh 等），使得网络能拟
合非线性。通常，称这个非线性函数为激活函数。一个典型的全连接神经网络如下所示：
1
图 1: 一个典型的全连接神经网络
1.1 前向传导
上图中，每个圆圈代表一个神经元（标上“+1”的是偏置节点，不算入神经元），从神经元引出
的连接是参数矩阵 w，从偏置节点引出的是参数向量 b。w 和 b 是整个网络最重要的参数。
1.1.1 输入层
假设输入 x = [x1; x2; x3]，令第一层的输入 z(1) 和激活输出 a(1) 相等，即 z(1) = a(1) = x。
1.1.2 隐藏层
第二层的输入为：
z(2)
1 = a(1)
z(2)
2 = a(1)
z(2)
3 = a(1)
1 w(2)
1 w(2)
1 w(2)
11 + a(1)
21 + a(1)
31 + a(1)
2 w(2)
2 w(2)
2 w(2)
12 + a(1)
22 + a(1)
32 + a(1)
3
1
3 w(2)
3 w(2)
3 w(2)
13 + b(2)
23 + b(2)
33 + b(2)
2
用向量简洁表达为：
其中，z(2) 2 R31; w(2) 2 R33; a(1) 2 R31; b(2) 2 R31
第二层的激活输出为：
z(2) = w(2)a(1) + b(2)
a(2) = f (z(2))
其中，f 为激活函数，a(2) 2 R31。
1.1.3 输出层
第三层输入：
其中，z(3) 2 R11; w(3) 2 R13; a(2) 2 R31; b(3) 2 R11
z(3) = w(3)a(2) + b(3)
2
第三层激活输出：
其中，f 为激活函数，a(3) 2 R11。特别地，记 a(3) 为 hw;b(x)
a(3) = f (z(3))
1.1.4 前向传导
因此，前向传导可以表示为：
z(l+1) = w(l+1)a(l) + b(l+1)
a(l+1) = f (z(l+1))
其中，l = 1; 2; :::; L 1，L 为神经网络的层数。
1.2 反向传播
假设神经网络的代价函数为
m∑
i=1
1
m
J(w; b) =
J(w; b; x(i); y(i))
其中:
1
2
即，网络的整体代价为所有训练样例的平均代价。
J(w; b; x(i); y(i)) =
(y(i) hw;b(x(i)))2
此处我们是要找到最佳的 w; b 使得 J(w; b) 即代价函数的值最小，因此 J 是关于 w; b 的函数，
其中 w; b 也不是标量，是很多 wij; bi 的集合。代价函数中没有显式的看到 w; b 的表达式，那是因
为用简洁的 hw;b(x(i)) 替换了。因此要强调的是：J 的展开表达式（假设能展开）中只有 w; b 才是
变量，其他都是已知的。
因此，根据梯度下降法的思想，对于每个 w(l)
ij , 我们只要往负梯度方向更新就可以了，即：
ij ; b(l)
ij
w(l)
ij := w(l)
@J
@w(l)
ij
@J
@b(l)
ij
b(l)
ij := b(l)
ij
向量化表达即为：
w(l) := w(l)
b(l) := b(l)
@J
@w(l)
@J
@b(l)
其中， 是学习率。
因此，只要能求出 w; b 的偏导数就能迭代更新，从而完成整个算法。看似简单，但却困难。因
为 J(w; b) 是很难写出显式表达式的，从而很难对每个 wij; bij 都求出偏导，主要原因是网络是分层
的进而 w; b 也是分层，这才导致了偏导的难求，从而才有了反向传播。
既然 w; b 是分层的，那么很自然地也可以分层地求 w; b 的偏导。那么很自然的，需要找到一个
递推的结构来表达偏导。观察到前向传导中的结构 z(l+1) = w(l+1)a(l) + b(l+1)，只要求出 z(l+1) 的偏
导，自然就可以求出 w(l+1); b(l+1) 的偏导（矩阵、向量的求导形式类似标量，a(l) 视为常量）。
3
考虑单个样例的情形，当 l 为输出层时 (l=3)，有：
(y a(3))2 =
(y h(x))2 =
@
@
@J
@z(3) =
(3) =
@z(3)
其中，◦ 是按元素 (element-wise) 相乘。
@z(3)
1
2
1
2
@
@z(3)
1
2
(y f (z(3)))2 = (y h(x))◦ f
′
(z(3))
当 l 为非输出层（隐藏层）时 (l=2)，有：
(2) =
@J
@z(2) =
@J
@z(3)
@z(3)
@z(2) = (3) @z(3)
@z(2) = (3)
@
@z(2) [w(2)f (z(2)) + b(2)] = w(2)f
′
(z(2)) ◦ (3)
因此：
所以：
(L) = (y h(x)) a(L)(l) = w(l)a(l) (l+1); (l = 2; :::; L 1)
@J
@w(l) =
@J
@z(l)
@z(l)
@w(l) = (l) (a(l1))T @J
@b(l) =
@J
@z(l)
@z(l)
@b(l) = (l); (l = 2; :::; L)
2 卷积神经网络
2.1 卷积
假设有矩阵 A33 和 B22：
A =
[
]
1 2
3 4
4 5 6
2664 1 2 3
[
7 8 9
3775 B =
]
那么 B 卷积 A 的结果就是让 B 在矩阵 A 上滑动，换言之，就是 B 与 A 的所有 2×2 连续子
矩阵做“对应元素积之和”运算，所以，此时的结果 C 应该为：
C =
37 47
67 77
因此，假设 A 的大小为 ha wa，B 的大小为 hb wb（其中 ha hb; wa wb），则 C 的大小
为 (ha hb + 1) (wa wb + 1)，矩阵 B 称为卷积核或滤波器 (filter)，矩阵 C 称为特征图 (feature
map)。上述运算称为窄卷积，若矩阵 A 预先上下各添加 hb 1 行零向量，左右各添加 wb 1 列
零向量，再与 B 卷积，则称为宽卷积。窄卷积和宽卷积分别用 conv2(A, B, ’valid’)和 conv2(A, B,
’full’)表示。
2.2 池化
假设矩阵 C 为 6 4 的矩阵，池化窗口为 2 2，则按照池化窗口大小将矩阵 C 分割成 6 块不
相交的 2 2 小矩阵，对对每个块中的所有元素做求和平均操作，称为平均池化，取最大值则称为
最大池化。得到的矩阵 S 称为 pool map。如：
26666666664
C =
37777777775
1 2 3 4
1 2 3 4
5 6 7 8
5 6 7 8
9 0 1 2
9 0 1 2
4
若平均池化，则：
若最大池化，则：
S =
5:5 7:5
26641:5 3:5
3775
3775
26642 4
4:5 1:5
S =
6 8
由于池化也称为下采样，用 S = down(C) 表示，为了使得池化层具有可学习性，一般令：
9 2
S = down(C) + b
其中， 和 b 为标量参数。
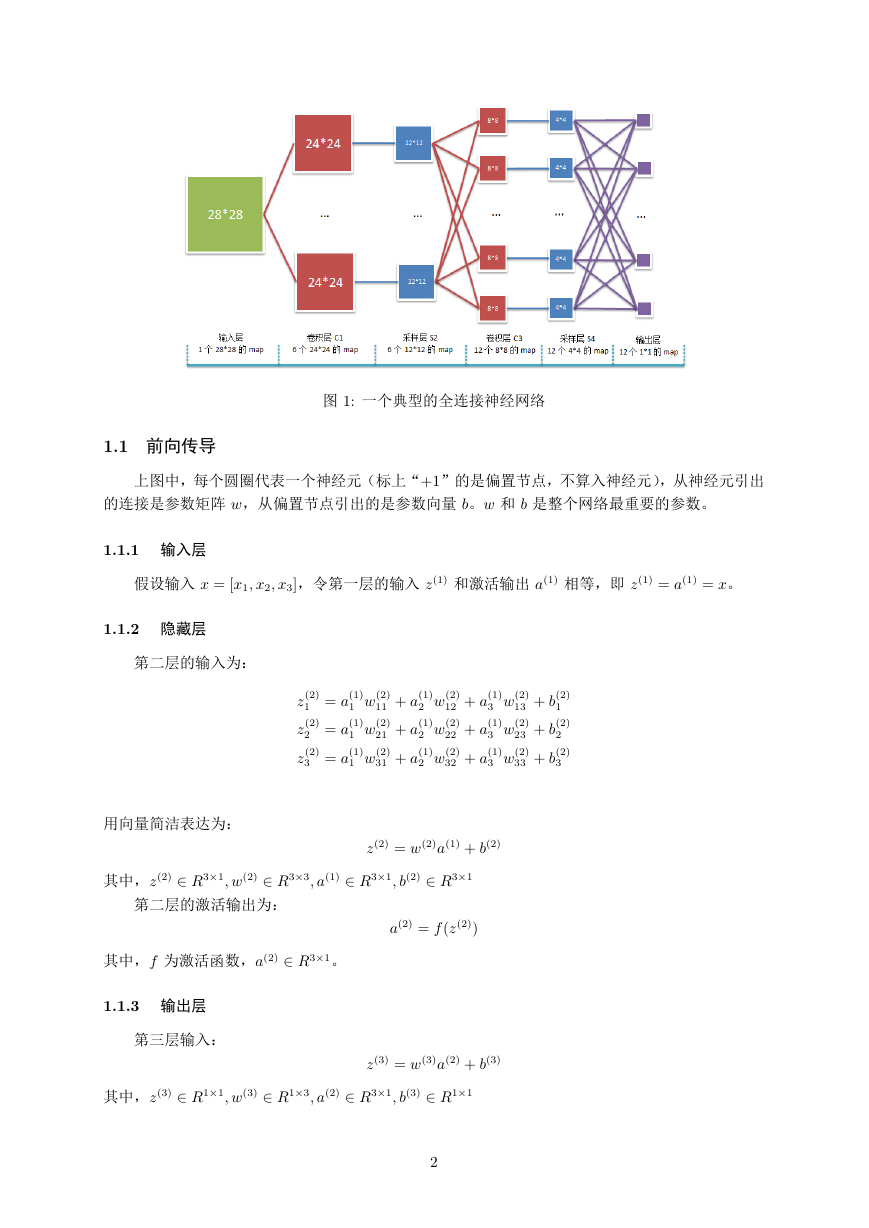
2.3 卷积神经网络
卷积神经网络是权值共享，非全连接的神经网络。以 2 个卷积层和 2 个池化层的卷积神经网络
为例，其结构图如下：cnn
2.3.1 前向传导
C1 层：卷积神经网络的输入是 28 28 的矩阵 A，经过 F1 个 5 5 的卷积核 K 1
i (i = 1; 2; :::; F1)
的卷积生成 F1 个 24 24 大小的 feature maps：
′
′
valid
) + b1
i
C 1
i = conv2(A; K 1
i ;
u1
i = C 1
i
a1
i = f (u1
i )
S2 层：接着池化，池化窗口为 2 2，一个 24 24 的 feature map 池化成一个 12 12 大小的
pool map，共生成 F1 个 pool maps：
i down(a1
i ) + b2
i
i = 2
S2
i = S2
u2
i
i = f (u2
a2
i )
C3 层：接着再次卷积，C3 层中每个 8 8 的 feature map C 3
i 都由 S2 中的所有 F1 个 pool
maps 经过 F1 个 5 5 的卷积核 K 3
ij(j = 1; 2; :::; F1)，共生成 F3 个 feature maps：
′
′
valid
) + b3
ij
F1∑
C 3
i =
conv2(a2
j ; k3
ij;
j=1
i = C 3
u3
i
i = f (u3
a3
i )
5
S4 层：接着再次池化，池化窗口为 2 2，一个 8 8 的 feature map 池化成一个 4 4 大小的
pool map，共生成 F3 个 pool maps：
i down(a3
i ) + b4
i
S4
i = 4
i = S4
u4
i
i = f (u4
a4
i )
全连接层：最后，将 a4
i (i = 1; 2; :::; F3) 顺序展开成向量，并有序连接成一个长向量，作为全连
接层网络的输入。
2.3.2 反向传播
卷积神经网络的反向传播本质上是和 BP 神经网络是一致的，区别在于全连接和非全连接：
在反向求导时，卷积神经网络要明确参数连接了哪些神经元；而全连接的普通神经网络中的相邻两
层的神经元都是与另一层的所有神经元相连的，因此反向求导时非常简单。
全连接层 全连接层的反向求导是与普通神经网络的反向求导是一致的：
卷积层 假设当前卷积层为 l，下一层为池化层 l + 1，上一层也为池化层 l 1。那么从 l 1
层到 l 层有：
a(l)
i = f (u(l)
i ) = f (
conv2(a(l1)
j
; K (l)
ij ) + b(l)
ij )
其中，Nl1 为 l 1 层 pool maps 的个数。如，当 l = 1 时，Nl1 = 1；当 l = 3 时，Nl1 = F1。
为了求得卷积层 l 的各个神经元的 ，关键是要必须弄清楚该神经元与 l + 1 层中的哪些神
经元连接，因为求该神经元的 时，只与这些神经元相关。递推的方式与全连接的神经网络的不同
之处在于：1. 卷积层 l 的各个神经元的 只和 l + 1 层的相关神经元有关 2. 卷积层 l 到池化层 l + 1
i 需要上采样 up 成卷积层的矩阵维度。定义 up
做了下采样运算，使得矩阵维度减小，因此，(l+1)
运算为（若上采样窗口为 2 2）：
@J
@w(l) = (l)(a(l1))T
@J
@b(l) = (l)
Nl1∑
j=1
[
]
2666641 1 2 2
1 1 2 2
3 3 4 4
377775
3 3 4 4
i = (l+1)
(l)
i
@J
@b(l)
i
=
∑
(a(u(l)
∑
i ) ◦ up(l+1
(i)st
i
))
s;t
i )st(P (l1)
((l)
j
)st
=
st
up(
1 2
3 4
) =
因此，有：
@J
@K (l)
ij
其中，()st 遍历 的所有元素，(P (l1)
j
矩阵。
6
)st 是 ((l)
i ) 所连接的 l 1 层中 al1
j 中相关的元素构成的
池化层假设当前池化层为 l，下一层为全连接层，那么当前池化层就是全连接层的输入，可以根
据全连接层的 BP 求导公式递推算出。因此只需讨论下一层 l + 1 为卷积层的情形，上一层 l 1 也
为卷积层，该情形下有：
a(l)
i = f ((l)
i down(a(l1)
i
) + b(l)
i )
同样地，为了求得池化层 l 的各个神经元的 ，关键是要必须弄清楚该神经元与 l + 1 层中的哪
些神经元连接，因为求该神经元的 时，只与这些神经元相关。递推的方式与全连接的神经网络的
不同之处在于：1. 池化层 l 的各个神经元的 只和 l + 1 层的相关神经元有关 2. 池化层 l 到卷积层
l + 1 做了窄卷积运算，使得矩阵维度减小，因此，l+1
i 需要与相应的卷积核做宽卷积运算使得矩阵
维度扩展回去。因此，有：
Nl∑
j=1
(l)
i =
a(l)
i
; K (l+1)
ji
′
;
′
)
f ull
j
◦ conv2((l+1)
∑
∑
((l)
@J
@b(l)
i
=
s;t
i )st
@J
@(l)
i
=
s;t
◦ d(l1)
i
)st
((l)
i
其中，()st 遍历 的所有元素，d(l1)
i
= down(a(l1)
i
)。
本文来源：http://tech.youmi.net/2016/07/163347168.html
参考资料
1. UFLDL Tutorial
2. GradientBased Learning Applied to Document Recognition
3. Notes on Convolutional Neural Networks
7
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
