2003年重庆高考文科数学真题及答案.doc-资料库

第1页 / 共16页

第2页 / 共16页

第3页 / 共16页

第4页 / 共16页

第5页 / 共16页

第6页 / 共16页

第7页 / 共16页

第8页 / 共16页

2003 年重庆高考文科数学真题及答案一、选择题（共 12 小题，每小题 5 分，满分 60 分） 1．（5 分）直线 y＝2x关于 x轴对称的直线方程为（） A． B． C．y＝﹣2x D．y＝2x 2．（5 分）已知 x∈（，0），cosx ，则 tan2x等于（） A． B． C． D． 3．（5 分）抛物线 y＝ax2 的准线方程是 y＝2，则 a的值为（） A． B． C．8 D．﹣8 4．（5 分）等差数列{an}中，已知 a1 ，a2+a5＝4，an＝33，则 n为（） A．48 B．49 C．50 D．51 5．（5 分）双曲线虚轴的一个端点为 M，两个焦点为 F1、F2，∠F1MF2＝120°，则双曲线的离心率为（） A． B． C． D． 6．（5 分）设函数若 f（x0）＞1，则 x0 的取值范围是（） A．（﹣1，1） B．（﹣1，+∞） C．（﹣∞，﹣2）∪（0，+∞） D．（﹣∞，﹣1）∪（1，+∞） 7．（5 分）已知 f（x5）＝lgx，则 f（2）＝（） A．lg2 B．lg32 C． D． 8．（5 分）函数 y＝sin（x+φ）（0≤φ≤π）是 R上的偶函数，则φ＝（） A．0 B． C． D．π

9．（5 分）已知点（a，2）（a＞0）到直线 l：x﹣y+3＝0 的距离为 1，则 a＝（） A． B． C． D． 10．（5 分）已知圆锥的底面半径为 R，高为 3R，它的内接圆柱的底面半径为，该圆柱的全面积为（） A．2πR2 B． C． D． 11．（5 分）已知长方形的四个顶点 A（0，0），B（2，0），C（2，1）和 D（0，1），一质点从 AB的中点 P0 沿与 AB夹角为θ的方向射到 BC上的点 P1 后，依次反射到 CD、DA和 AB 上的点 P2、P3 和 P4（入射角等于反射角）若 P4 与 P0 重合，则 tgθ＝（） A． B． C． D．1 12．（5 分）棱长都为的四面体的四个顶点在同一球面上，则此球的表面积为（） A．3π B．4π C．3 D．6π 二、填空题（共 4 小题，每小题 4 分，满分 16 分） 13．（4 分）不等式的解集是． 14．（4 分）在的展开式中，x3 的系数是（用数字作答） 15．（4 分）在平面几何里，有勾股定理“设△ABC的两边 AB，AC互相垂直，则 AB2+AC2＝BC2”，拓展到空间，类比平面几何的勾股定理，研究三棱锥的侧面面积与底面面积间的关系，可以得出正确的结论是：“设三棱锥 A﹣BCD的三个侧面 ABC、ACD、ADB两两互相垂直，则．” 16．（4 分）如图，一个地区分为 5 个行政区域，现给地图着色，要求相邻区域不得使用同一颜色．现有 4 种颜色可供选择，则不同的着色方法共有种．（以数字作答）

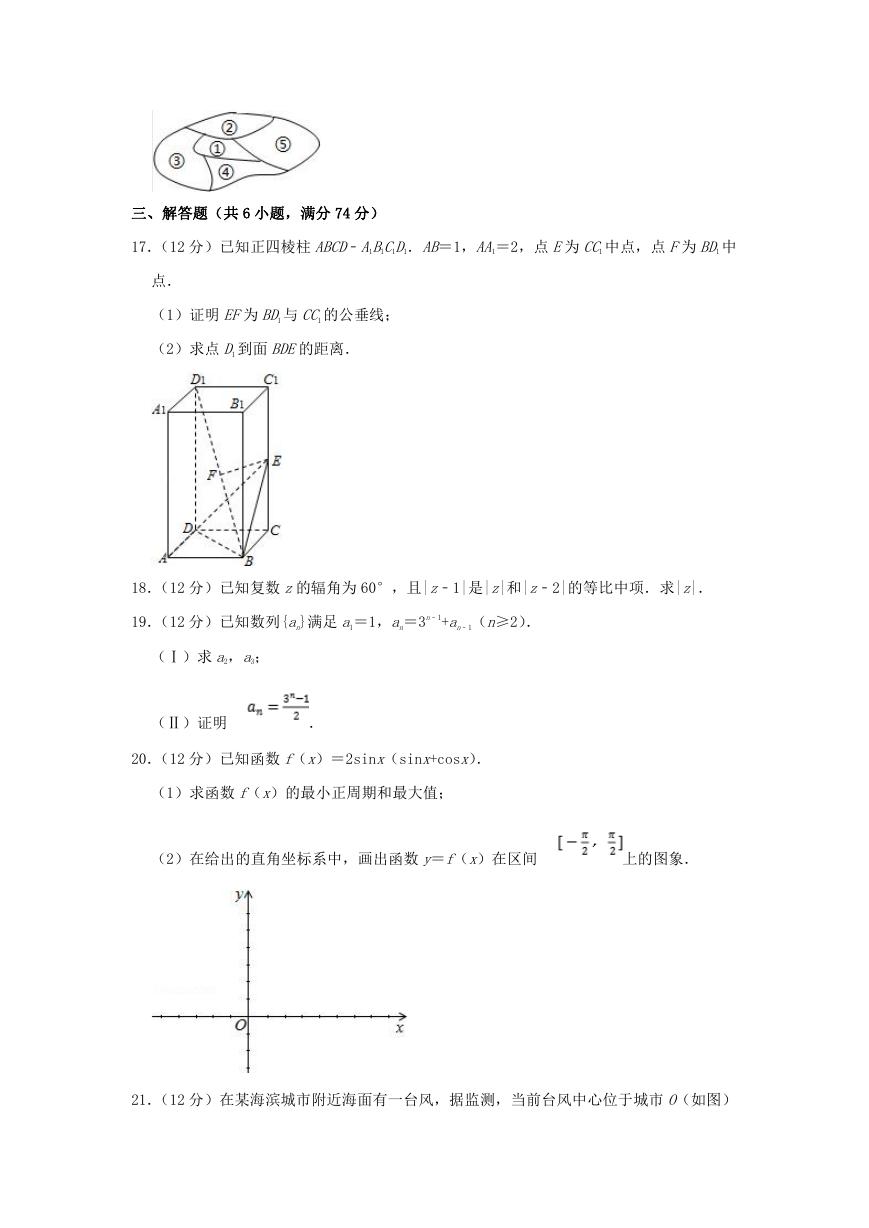
三、解答题（共 6 小题，满分 74 分） 17．（12 分）已知正四棱柱 ABCD﹣A1B1C1D1．AB＝1，AA1＝2，点 E为 CC1 中点，点 F为 BD1 中点．（1）证明 EF为 BD1 与 CC1 的公垂线；（2）求点 D1 到面 BDE的距离． 18．（12 分）已知复数 z的辐角为 60°，且|z﹣1|是|z|和|z﹣2|的等比中项．求|z|． 19．（12 分）已知数列{an}满足 a1＝1，an＝3n﹣1+an﹣1（n≥2）．（Ⅰ）求 a2，a3；（Ⅱ）证明． 20．（12 分）已知函数 f（x）＝2sinx（sinx+cosx）．（1）求函数 f（x）的最小正周期和最大值；（2）在给出的直角坐标系中，画出函数 y＝f（x）在区间上的图象． 21．（12 分）在某海滨城市附近海面有一台风，据监测，当前台风中心位于城市 O（如图）

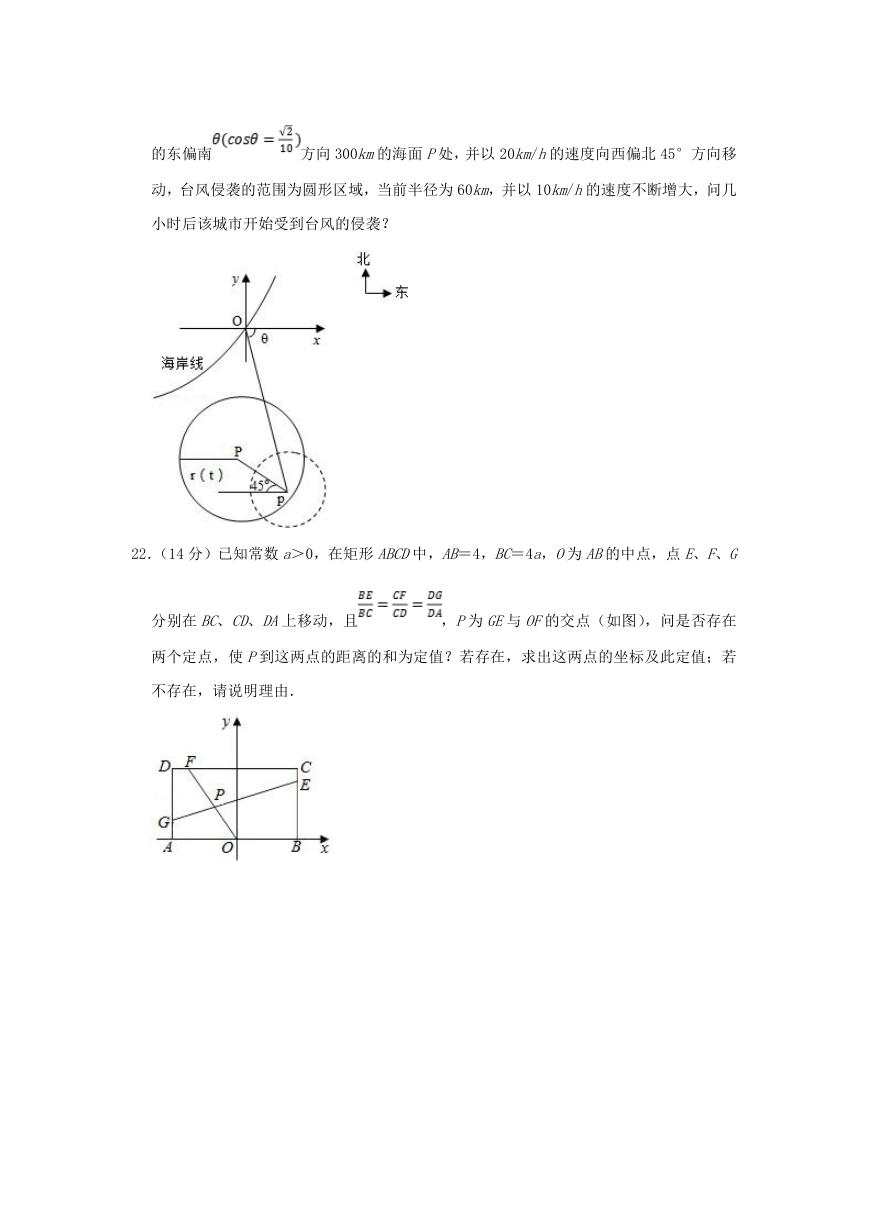
的东偏南方向 300km的海面 P处，并以 20km/h的速度向西偏北 45°方向移动，台风侵袭的范围为圆形区域，当前半径为 60km，并以 10km/h的速度不断增大，问几小时后该城市开始受到台风的侵袭？ 22．（14 分）已知常数 a＞0，在矩形 ABCD中，AB＝4，BC＝4a，O为 AB的中点，点 E、F、G 分别在 BC、CD、DA上移动，且，P为 GE与 OF的交点（如图），问是否存在两个定点，使 P到这两点的距离的和为定值？若存在，求出这两点的坐标及此定值；若不存在，请说明理由．

2003 年全国统一高考数学试卷（文科）参考答案与试题解析一、选择题（共 12 小题，每小题 5 分，满分 60 分） 1．（5 分）直线 y＝2x关于 x轴对称的直线方程为（） A． B． C．y＝﹣2x D．y＝2x 【解答】解：∵直线 y＝f（x）关于 x对称的直线方程为 y＝﹣f（x）， ∴直线 y＝2x关于 x对称的直线方程为： y＝﹣2x．故选：C． 2．（5 分）已知 x∈（，0），cosx ，则 tan2x等于（） A． B． C． D．【解答】解：∵cosx ，x∈（，0）， ∴sinx ．∴tanx ． ∴tan2x 故选：D．． 3．（5 分）抛物线 y＝ax2 的准线方程是 y＝2，则 a的值为（） A． B． C．8 D．﹣8 【解答】解：抛物线 y＝ax2 的标准方程是 x2 y，则其准线方程为 y 2，

所以 a ．故选：B． 4．（5 分）等差数列{an}中，已知 a1 ，a2+a5＝4，an＝33，则 n为（） A．48 B．49 C．50 D．51 【解答】解：设{an}的公差为 d， ∵ ，a2+a5＝4， ∴ d 4d＝4，即 5d＝4，解得 d ． ∴an （n﹣1），令 an＝33，即 33，解得 n＝50．故选：C． 5．（5 分）双曲线虚轴的一个端点为 M，两个焦点为 F1、F2，∠F1MF2＝120°，则双曲线的离心率为（） A． B． C． D．【解答】解：根据双曲线对称性可知∠OMF2＝60°， ∴tan∠OMF2 ，即 c b， ∴a b，

∴e ．故选：B． 6．（5 分）设函数若 f（x0）＞1，则 x0 的取值范围是（） A．（﹣1，1） B．（﹣1，+∞） C．（﹣∞，﹣2）∪（0，+∞） D．（﹣∞，﹣1）∪（1，+∞）【解答】解：当 x0≤0 时，，则 x0＜﹣1，当 x0＞0 时，则 x0＞1，故 x0 的取值范围是（﹣∞，﹣1）∪（1，+∞），故选：D． 7．（5 分）已知 f（x5）＝lgx，则 f（2）＝（） A．lg2 B．lg32 C． D．【解答】解：令 x5＝2， ∴得 x ， ∵f（x5）＝lgx， ∴f（2）＝lg lg2．故选：D． 8．（5 分）函数 y＝sin（x+φ）（0≤φ≤π）是 R上的偶函数，则φ＝（） A．0 B． C． D．π 【解答】解：当φ＝0 时，y＝sin（x+φ）＝sinx为奇函数不满足题意，排除 A；当φ 时，y＝sin（x+φ）＝sin（x ）为非奇非偶函数，排除 B；

当φ 时，y＝sin（x+φ）＝cosx，为偶函数，满足条件．当φ＝π时，y＝sin（x+φ）＝﹣sinx，为奇函数，故选：C． 9．（5 分）已知点（a，2）（a＞0）到直线 l：x﹣y+3＝0 的距离为 1，则 a＝（） A． B． C． D．【解答】解：由点到直线的距离公式得：， ∵a＞0， ∴a ．故选：C． 10．（5 分）已知圆锥的底面半径为 R，高为 3R，它的内接圆柱的底面半径为，该圆柱的全面积为（） A．2πR2 B． C． D．【解答】解：设圆锥内接圆柱的高为 h，则，解得，所以圆柱的全面积为：s＝2 ．故选：B． 11．（5 分）已知长方形的四个顶点 A（0，0），B（2，0），C（2，1）和 D（0，1），一质点从 AB的中点 P0 沿与 AB夹角为θ的方向射到 BC上的点 P1 后，依次反射到 CD、DA和 AB 上的点 P2、P3 和 P4（入射角等于反射角）若 P4 与 P0 重合，则 tgθ＝（） A． B． C． D．1 【解答】解：由于若 P4 与 P0 重合，故 P2、P3 也都是所在边的中点，因为 ABCD是长方形，

资料库

2003年重庆高考文科数学真题及答案.doc

相关推荐

高考

热门标签

最新资料