java画bezier曲线.doc-资料库

fm377417-4364052-4744300845399605352.doc.pdf-第1页.png

第1页 / 共13页

fm377417-4364052-4744300845399605352.doc.pdf-第2页.png

第2页 / 共13页

fm377417-4364052-4744300845399605352.doc.pdf-第3页.png

第3页 / 共13页

fm377417-4364052-4744300845399605352.doc.pdf-第4页.png

第4页 / 共13页

fm377417-4364052-4744300845399605352.doc.pdf-第5页.png

第5页 / 共13页

fm377417-4364052-4744300845399605352.doc.pdf-第6页.png

第6页 / 共13页

fm377417-4364052-4744300845399605352.doc.pdf-第7页.png

第7页 / 共13页

fm377417-4364052-4744300845399605352.doc.pdf-第8页.png

第8页 / 共13页

计算机图形学课程设计题专班目：Bezier 曲线的绘制业：计算机应用技术级：计科姓名：王莹学号： 40910045 第 1 页共 13 页

目录 1. 前言 ............................................................................................................................................ 3 2. 实例说明 .................................................................................................................................... 3 2.1 线性贝塞尔曲线................................................................................................................. 3 2.2 二次方贝塞尔曲线 .............................................................................................................. 3 2.3 三次方贝塞尔曲线 ............................................................................................................. 4 3.算法分析 ......................................................................................................................................... 4 3.1 一般化............................................................................................................................... 4 3.2 术语 ..................................................................................................................................... 4 3.3 注解 ..................................................................................................................................... 5 3.4 建构贝塞尔曲线................................................................................................................. 5 3.4.1 线性曲线................................................................................................................... 5 3.4.2 二次曲线 .................................................................................................................. 6 3.4.3 高阶曲线 .................................................................................................................. 6 3.5 升阶函数 ............................................................................................................................. 7 4. 程序文档说明 ............................................................................................................................... 8 5 程序源代码 .................................................................................................................................... 8 6 实验结果抓图 .............................................................................................................................. 11 7 参考文献 ...................................................................................................................................... 13 第 2 页共 13 页

1. 前言在数学的数值分析领域中，贝塞尔曲线（Bézier 曲线）是电脑图形学中相当重要的参数曲线。更高维度的广泛化贝塞尔曲线就称作贝塞尔曲面，其中贝塞尔三角是一种特殊的实例。贝塞尔曲线于 1962 年，由法国工程师皮埃尔·贝塞尔（Pierre Bézier）所广泛发表，他运用贝塞尔曲线来为汽车的主体进行设计。贝塞尔曲线最初由 Paul de Casteljau 于 1959 年运用 de Casteljau 算法开发，以稳定数值的方法求出贝塞尔曲线。贝塞尔曲线是应用于二维图形应用程序的数学曲线。曲线的定义有四个点：起始点、终止点（也称锚点）以及两个相互分离的中间点。滑动两个中间点，贝塞尔曲线的形状会发生变化。十九世纪六十年代晚期，Pierre Bézier 应用数学方法为雷诺公司的汽车制造业描绘出了贝塞尔曲线。贝塞尔曲线就是这样的一条曲线，它是依据四个位置任意的点坐标绘制出的一条光滑曲线。在历史上，研究贝塞尔曲线的人最初是按照已知曲线参数方程来确定四个点的思路设计出这种矢量曲线绘制法。贝塞尔曲线的有趣之处更在于它的“皮筋效应”~也就是说，随着点有规律地移动，曲线将产生皮筋伸引一样的变换，带来视觉上的冲击。19 世纪 70 年代，法国数学家 Pierre Bézier 第一个研究了这种矢量绘制曲线的方法，并给出了详细的计算公式，因此按照这样的公式绘制出来的曲线就用他的姓氏来命名~是为贝塞尔曲线。 2. 实例说明 2.1 线性贝塞尔曲线给定点 P0、P1，线性贝塞尔曲线只是一条两点之间的直线。这条线由下式给出：且其等同于线性插值。 2.2 二次方贝塞尔曲线二次方贝塞尔曲线的路径由给定点 P0、P1、P2 的函数 B（t）追踪： TrueType 字型就运用了以贝塞尔样条组成的二次贝塞尔曲线。。第 3 页共 13 页

2.3 三次方贝塞尔曲线 P0、P1、P2、P3 四个点在平面或在三维空间中定义了三次方贝塞尔曲线。曲线起始于 P0 走向 P1，并从 P2 的方向来到 P3。一般不会经过 P1 或 P2；这两个点只是在那里提供方向资讯。P0 和 P1 之间的间距，决定了曲线在转而趋进 P3 之前，走向 P2 方向的“长度有多长”。曲线的参数形式为：现代的成象系统，如 PostScript、Asymptote 和 Metafont，运用了以贝塞尔样条组成的三次贝塞尔曲线，用来描绘曲线轮廓。 3.算法分析 3.1 一般化阶贝塞尔曲线可如下推断。给定点 P0、P1、…、Pn，其贝塞尔曲线即例如：如上公式可如下递归表达：用表示由点 P0、P1、…、Pn 所决定的贝塞尔曲线。则用平常话来说，阶的贝塞尔曲线，即双阶贝塞尔曲线之间的插值。 3.2 术语一些关于参数曲线的术语，有第 4 页共 13 页

即多项式又称作 n 阶的伯恩斯坦基底多项式，定义 00 = 1。点 Pi 称作贝塞尔曲线的控制点。多边形以带有线的贝塞尔点连接而成，起始于 P0 并以 Pn 终止，称作贝塞尔多边形（或控制多边形）。贝塞尔多边形的凸包（convex hull）包含有贝塞尔曲线。 3.3 注解（1）开始于 P0 并结束于 Pn 的曲线，即所谓的端点插值法属性。（2）曲线是直线的充分必要条件是所有的控制点都位在曲线上。同样的，贝塞尔曲线是直线的充分必要条件是控制点共线。（3）曲线的起始点（结束点）相切于贝塞尔多边形的第一节（最后一节）。（4）一条曲线可在任意点切割成两条或任意多条子曲线，每一条子曲线仍是贝塞尔曲线。（5）一些看似简单的曲线（如圆）无法以贝塞尔曲线精确的描述，或分段成贝塞尔曲线（虽然当每个内部控制点对单位圆上的外部控制点水平或垂直的的距离为时，分成四段的贝塞尔曲线，可以小于千分之一的最大半径误差近似于圆）。（6）位于固定偏移量的曲线（来自给定的贝塞尔曲线），又称作偏移曲线（假平行于原来的曲线，如两条铁轨之间的偏移）无法以贝塞尔曲线精确的形成（某些琐屑实例除外）。无论如何，现存的启发法通常可为实际用途中给出近似值。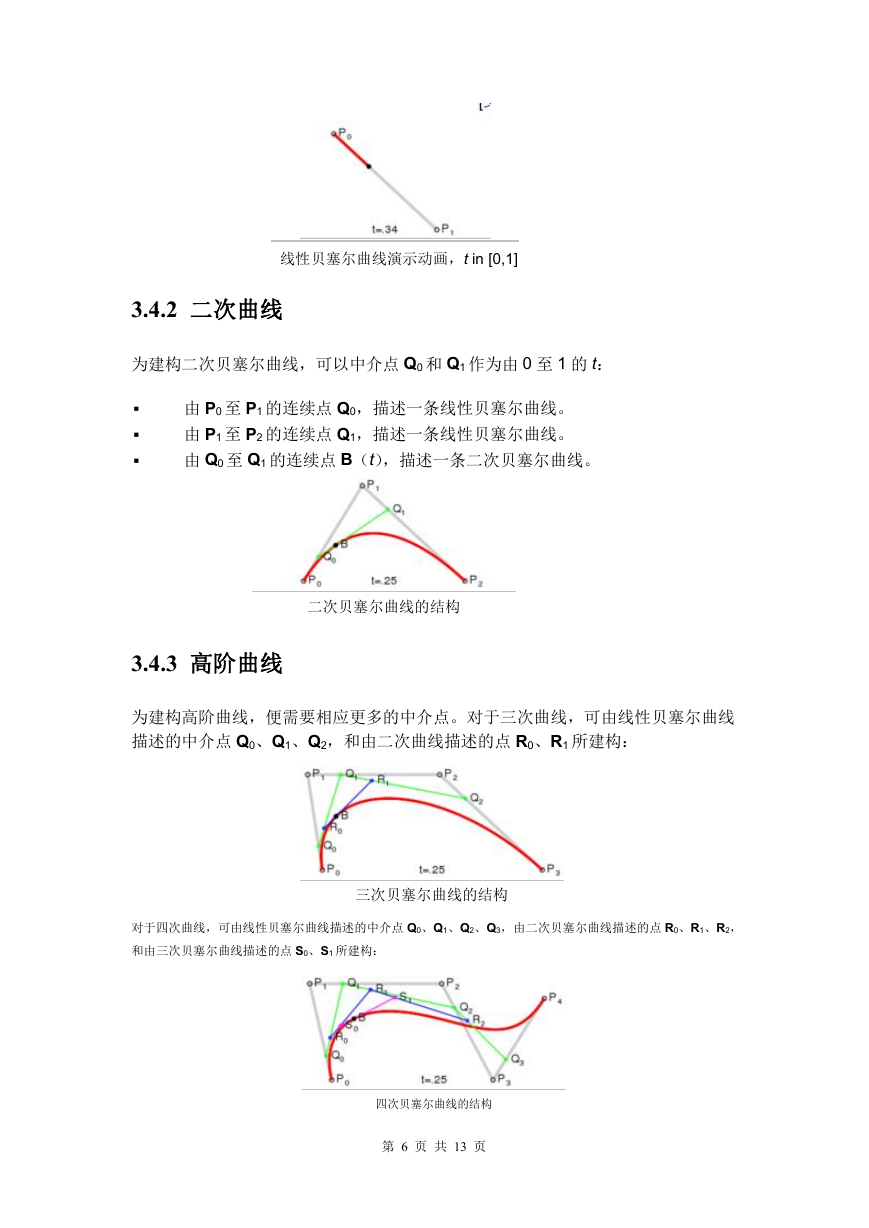 3.4 建构贝塞尔曲线 3.4.1 线性曲线线性贝塞尔曲线函数中的 t 会经过由 P0 至 P1 的 B（t）所描述的曲线。例如当 t=0.25 时，B（t）即一条由点 P0 至 P1 路径的四分之一处。就像由 0 至 1 的连续 t，B（t）描述一条由 P0 至 P1 的直线。第 5 页共 13 页

线性贝塞尔曲线演示动画，t in [0,1] 3.4.2 二次曲线为建构二次贝塞尔曲线，可以中介点 Q0 和 Q1 作为由 0 至 1 的 t：    由 P0 至 P1 的连续点 Q0，描述一条线性贝塞尔曲线。由 P1 至 P2 的连续点 Q1，描述一条线性贝塞尔曲线。由 Q0 至 Q1 的连续点 B（t），描述一条二次贝塞尔曲线。二次贝塞尔曲线的结构 3.4.3 高阶曲线为建构高阶曲线，便需要相应更多的中介点。对于三次曲线，可由线性贝塞尔曲线描述的中介点 Q0、Q1、Q2，和由二次曲线描述的点 R0、R1 所建构：三次贝塞尔曲线的结构对于四次曲线，可由线性贝塞尔曲线描述的中介点 Q0、Q1、Q2、Q3，由二次贝塞尔曲线描述的点 R0、R1、R2，和由三次贝塞尔曲线描述的点 S0、S1 所建构：四次贝塞尔曲线的结构第 6 页共 13 页

3.5 升阶函数 n 次贝塞尔曲线可以转换为一个形状完全相同的 n+1 次贝塞尔曲线。这在软件只支援特定阶次的贝塞尔曲线时很有用。例如，Cairo 只支援三次贝塞尔曲线，你就可以用升阶的方法在 Cairo 画出二次贝塞尔曲线。我们利用这个特性来做升阶。我们把曲线方程式中每一项都乘上 (1 − t) 或 t，让每一项都往上升一阶。以下是将二阶升为三阶的范例对任何的 n 值，我们都可以使用以下等式式中和可以任意挑选。因此，新的控制点为[1] 第 7 页共 13 页

4. 程序文档说明 MyFrame5 完成设置面板的功能，并在需要时重画。 Paint 完成鼠标左键点击画点的功能。 drawBezier 完成最后阶段的运算及绘制 Bezier 曲线。 Sf 完成初步运算。 5 程序源代码 package bezier; import java.awt.Color; import java.awt.Graphics; import java.awt.Point; import java.awt.event.MouseAdapter; import java.awt.event.MouseEvent; import java.util.ArrayList; import java.util.Iterator; import javax.swing.JFrame; import javax.swing.JOptionPane; class MyFrame5 extends JFrame{ ArrayList points=new ArrayList(); int si; MyFrame5(String s){ super(s); this.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE); points=new ArrayList(); setLayout(null); setBounds(300,300,600,400); this.setBackground(new Color(204,204,255)); setVisible(true); JOptionPane.showMessageDialog(null,"按鼠标左键画控制点，按右键结束画点 "); this.addMouseListener(new java.awt.event.MouseAdapter() { public void mouseClicked(java.awt.event.MouseEvent e) { if(e.getButton() == MouseEvent.BUTTON1){ points.add(new Point(e.getX(),e.getY())); repaint(); //让 Frame 强制重画 } 第 8 页共 13 页

资料库

java画bezier曲线.doc

相关推荐

开发技术

热门标签

最新资料