基于粒子群优化算法的无功优化.pdf

发布时间：2022-05-29 发布人：admin 分类：说明书资料大小：0.28M 资料格式：pdf 举报版权申诉

weixin_38748239-12122248-72d98ba511bc4063018ddf18589b2576.pdf-第1页.png

第1页 / 共6页

weixin_38748239-12122248-72d98ba511bc4063018ddf18589b2576.pdf-第2页.png

第2页 / 共6页

weixin_38748239-12122248-72d98ba511bc4063018ddf18589b2576.pdf-第3页.png

第3页 / 共6页

weixin_38748239-12122248-72d98ba511bc4063018ddf18589b2576.pdf-第4页.png

第4页 / 共6页

weixin_38748239-12122248-72d98ba511bc4063018ddf18589b2576.pdf-第5页.png

第5页 / 共6页

weixin_38748239-12122248-72d98ba511bc4063018ddf18589b2576.pdf-第6页.png

第6页 / 共6页

文本预览

中国科技论文在线 http://www.paper.edu.cn 基于粒子群优化算法的无功优化李银萍中国矿业大学信电学院，江苏徐州（221008） E-mail: liyinping1010@163.com 摘要:无功优化是减少电网损耗的有效措施。本文采用引入了自适应惯性权重系数和变异算子的粒子群算法对电力系统进行无功优化，并对 IEEE30 节点测试系统进行了无功优化计算。计算结果表明，这种优化方法可以较好地协调算法的局部与全局搜索能力，有效解决电力系统的无功优化问题。关键词：粒子群算法；无功优化；电力系统中图分类号：TM714 1 引言随着国民经济的迅速发展，用电量的增加，电网的经济运行日益受到重视。而将无功功率进行合理分布可以有效减少网损，提高电网的运行经济性。近年来，现代启发式算法广泛应用于无功优化领域并取得了大量研究成果，如线性规划法、非线性规划法、混合整数法等，取得了一定的效果。但这类算法需要某些假设条件，如连续、导数存在及单峰等，而且在求解无功优化问题时，将整数变量视为连续变量参与优化计算，得到最优解后再进行归整。因此，采用常规算法求解无功优化问题时遇到的困难之一就是离散变量的归整问题。对于大规模的实际系统的无功优化，由规整产生的误差可能是不可以接受的。另外，无功优化还是一个多峰多极值问题，常规算法从初始运行点出发，沿着某一路径寻找最优解，往往容易陷于某个局部最优解，而达不到全局优化的目的[1]。粒子群优化算法(Partical Swarm Optimization - PSO)是 Kennedy 和 Eberhart 于 1995 年提出的一种多点搜索算法，由于其简便易行、依赖的经验参数较少、收敛速度快等特点，已被广泛应用，该算法在电力系统无功优化的问题中展现出优良特性。通过引入自适应惯性权重系数和变异算子对粒子群算法进行了改进，在一定程度上改善了算法的收敛能力和精度[2]。本文以调节发电机端电压，投切电容器和改变可调节变压器分接头为控制手段，采用改进粒子群优化算法求解无功优化问题。通过考虑各个粒子群的相互指导作用改善解的性能，即增强粒子群间的协同作用，以及引入惯性因子和扰动等策略来实现优化。虽然它也是从随机解出发，通过迭代寻找最优解，但它比遗传算法更为简单，通过追随当前搜索到的最优值来寻找全局最优。 2 基本粒子群算法原理粒子群算法是一种基于迭代模式的优化算法，最初被用于连续空间的优化。在连续空间坐标系中，粒子群算法的数序描述为：设粒子群体规模为 N，每个粒子在 D 维空间中的坐 iDx )，粒子 i (i=1,2,…,N)的速度定义为每次迭代粒标位置可表示为 ix =( 1ix , iDv )表示。于是，粒子 i (i=1,2,…,N) 在第 d 子移动的距离，用 iv =( (d=1,2,…,D)维子空间中的飞行速度 idv 根据下式进行调整： c rand ∗ 2 2ix ,…, 1iv , (2.1a) v v k k 1 ω+ = id id idx ,…, 2iv ,…, idv ,…, + c rand 1 1 ∗ ( p id x id ) − x id ) + 2 (p gd − -1-

中国科技论文在线 http://www.paper.edu.cn id v ⎧ ⎨ v ⎩ v = −= max v vif , id vif , > , v max v −< . id id max max 式(2.1a)中， gdp 是整个粒子群的历史最优位置记录，其与当前粒子的位置之差被用于改变当前粒子向群体最优值运动的增量分量，此增量还需要进行一定程度的随机化（运用 rand 随机发生器）； idp 是当前粒子的历史最优位置记录。类似地，它与当前粒子的位 rand 亦为随机发生器）；ω 为惯性因置之差也被用于该粒子的方向性随机运动设定（ (2.1b) *1 *2 子(inertia weight)，c1，c2 为加速常数(acceleration constants)。式(2.1b)中，对粒子的速度 iv 进行了最大速度控制，如果当前对粒子的加速将导致它在某维空间的速度分量 idv 超过该维的最大速度限额 maxv ，则该维的速度被限制为最大速度 maxv 。它决定了粒子在解空间中的搜索精度，如果 maxv 太高，粒子可能会飞过最优解；如果 maxv 太小，粒子容易陷入局部搜索空间而无法进行全局搜索[3]。粒子通过方程(2.2)调整自身的位置： x k 1 + id = x k id + v k 1 + id (2.2) 3 基于粒子群算法的无功优化 3.1 无功优化的数学模型从数学上讲，无功优化问题是一个动态、多目标、多约束、不确定性的非线性混合整数规划问题。电力系统无功优化的目标是，通过调节控制变量优化无功潮流的分布，改善系统的电压质量，减少电能传输损耗，从而降低运行成本和提高稳定运行水平。以系统安全性为出发点的目标主要有：使无功电源总注入或加权总注入最小；使各母线电压偏离规定值最小；使线路过负荷最小；使电压稳定裕度最大等。以系统运行的经济性为出发点的目标主要有：使运行费用即网损最小；使运行点偏离最优运行点最小等。这样，目标函数就包括了技术性能指标和经济指标。约束条件主要有：有功潮流方程、无功潮流方程、控制变量和状态变量的上、下限约束等。本文无功优化问题的数学模型目标函数为网络有功损耗最小，即： min ( f x x (3.1) ) , 1 2 T C TVQ , (3.1)式中：控制变量 x 1=[ (M ，M 为有约束的优化变量总数； Q C 为无功补偿装置构成的向量； CV 为发电机机端电压幅值构成的向量； BT 为可调变压器变比构成的向量；状态变量 x 2 为由全部负荷节点电压幅值和发电机无功功率构成的向量， T] ，x 1 ∈R ) T C T B , x 2 ∈ )(nR ，其中 n 为系统节点数。无功优化的约束条件有等式约束和不等式约束两类。（1）等式约束功率平衡方程： 1 （2）不等式约束保证系统正常运行的其他条件，包括：a. 控制变量约束：无功补偿装置容量的上下限； 2 g x x = ( ) 0 , -2-

中国科技论文在线 http://www.paper.edu.cn 机端电压幅值上下限；变压器可调变比的上下限。b. 状态变量约束：发电机无功出力上下限；节点电压上下限。本文将负荷节点电压幅值和发电机无功功率的越限用罚函数处理，这样得到一个增广的目标函数，最终将模型建立为： MinF = xxf , ( 1 2 ) + λ 1 Ni ∑ i 1 = VV ( i − i lim, ) λ + 2 Ng ∑ i 1 = QQ ( i − i ) (3.2) lim, = ,lim ,max V i ，，式（3.2）中： V ⎧⎪ i ⎨ V ⎪⎩ i 数， iN 为负荷节点个数， gN 3.2 粒子群优化算法求解无功优化步骤 V V i i V V i i ≥ ≤ ,min ,lim ,lim 为发动机节点个数。， Q i ,lim Q ⎧ i = ⎨ Q ⎩ i ， ,max ， ,min i Q Q i Q Q i i ≥ ≤ ， 1λ、 2λ 为罚系 ,lim ,lim 用粒子群算法求解无功优化问题时，将式(3.1)中定义的 x 1=[ T] 对应为粒子群中粒子的位置，可行域的边界由 Q C 、 CV 和 BT 的上下限确定。运用粒子群优化算法求解无功优化问题的过程描述如下： TVQ , T C T B T C , 步骤 1：输入系统数据，初始化粒子群。首先输入系统的结构、网络数据和控制参数，其中发电机节点电压的上下限、电容器容量的上下限、变压器分接头上下限等构成了解的可行域。其次确定粒子的维数 M(即一组控制变量中的变量数)，在 M 维可行域中随机产生 N 个粒子作为初始粒子群。这样，每个粒子的位置分别对应了系统中一组控制变量的取值。同时随机初始化各粒子的飞行速度。此时迭代次数 k=0。步骤 2：计算目标函数值。对群体中的每个粒子，分别进行潮流计算，得到每组控制变量取值下的有功网损，并判断是否违反节点电压以及发电机无功出力等约束，将电压及发电机无功越界值作为罚函数项计入到目标函数。步骤 3：记录两个极值。比较所有粒子对应的目标函数值，首先记录粒子 i(i=1,2，…， N)当前的个体极值 idP 及答应的目标函数值 F（ idp ）；从 idP 中确定整体极值 gdP ，并记录 gdP 答应的目标函数值 F（ gdp ）。步骤 4：更新 k=k+1。粒子根据式(2.1)更新各粒子的飞行速度，这样对于粒子 i 就得到一个确定的趋向 idp 和 gdp 的飞行速度。再根据式(2.2)更新粒子在解空间中的位置。 idp )=F(i，k+1)，(i=1，2，…N) 并相应地更新 F( 步骤 5：重新计算各个粒子此时的目标函数值，判断是否更新 idp 和 gdp ： (1) 对于粒子 i，比较第 k+1，次迭代中得到的函数值 F(i，k+1)与 F( idp )则 F( (2) 更新全部粒子的个体极值后，若 min{ F( gdp )=min{F( 步骤 6：判断是否收敛。当满足如下条件之一，迭代停止：全局最好位置连续 20 次无 idp )，i=1,2,…，N}，并相应更新 dg ，否则不更新。 idp )，(i=1，2，…，N)}

中国科技论文在线 http://www.paper.edu.cn 况，系统各节点电压、发电机无功出力等状态变量的数据，以及对应的网损值[3]。图 1 基本粒子群算法的流程图 3.3 粒子群算法在求解无功优化问题中的参数分析在 PSO 算法中有 3 个对算法性能有重要影响的参数：惯性权重系数（惯性系数）ω，加速常数 c1 和 c2。这 3 个参数的选取没有固定的法则，一般是根据设计者的经验事先给定。 3.3.1 粒子群体规模 N 和初始解群的选取粒子群规模 N 表示每一代粒子群中所含粒子的数目。当 N 取值较小时，PSO 的运算速度较快，但由于种群的多样性差，容易引起过早收敛；当 N 取值较大时，又会使 PSO 的寻优效率降低。适当选取 N，可保障种群的多样性和算法的搜索效率，其取值在 10-40。要保证算法的性能，首先要保证一定的群体规模。但是规模过大不仅无益于问题的求解反而导致计算量大幅增加，从而使计算时间大量延长，无法满足工程需要。本文算法取粒子个数为 30，其合理性将在算例中印证[1]。 3.3.2 惯性系数 ω 和最大迭代次数 Imax 惯性系数 ω 是一个控制参数，它实际上是调节粒子在迭代过程中飞行的步长，通过动态地调节惯性系数，可以控制粒子群在迭代过程中的空间活跃程度即迭代收敛速度，解决粒子的全局搜索能力和局部精细搜索能力的平衡性较差的问题。在迭代初期，需要粒子有较大的活跃度；而在迭代后期，粒子群已经搜索到极优解(局部最优解)周围，此时必须降低粒子的活跃程度、减小飞行步长，使得粒子能够在小空间范围内进行精细搜索，否则，粒子群的频繁大幅度跳跃，会导致粒子始终在围绕极优解的空间中跳跃而无法达到局部极值点。本文假定计算惯性系数 ω 呈线性下降，计算如下： ω ω = i max − ω ω − max Iter max min kI (3.3) 式(3.3)中： max I 为最大迭代次数，本文取 100； kI 为当前迭代次数； maxω 和 minω 为常数，经数值实验表明，实际计算中 maxω =0.9 和 minω =0.4 时能够取得较好的优化效果。 -4-

中国科技论文在线 3.3.3 最大飞行速度 Vmax http://www.paper.edu.cn 为获得较好的优化解，本文设置最大速度 maxV ，则粒了的速度取值范围为[— maxV ， maxV ]， maxV 决定了个体极值与整体极值之间区域的分辨率(或称精度)。如果 maxV 过大，粒子可能掠过最优解；如果 maxV 太小，粒子在局部最优解的邻域之外不能进行足够搜索，可能导致陷人局部最优解。本文设 maxV 为控制变量取值范围的 10 ％，即 V max ，P=10。 x (1,max) x (1,min) / P = ( − ) 3.5 仿真计算为了检验上述利用粒子群优化算法求解无功优化问题的有效性，本文使用 IEEE30[6， 7]节点试验系统进行计算。系统参数均用标么值表示，其基准功率是 100MW。以 IEEE30 节点系统为例。该系统包括 6 台发电机，4 台可调变压器及 2 个无功补偿点。计算中系统参数用标么值表示，基准功率 100MW。P-V 节点和平衡节点的电压上下限设置为 0.9 和 1.1。 P-V 节点的电压上下限分别设置为 0.95 和 1.05。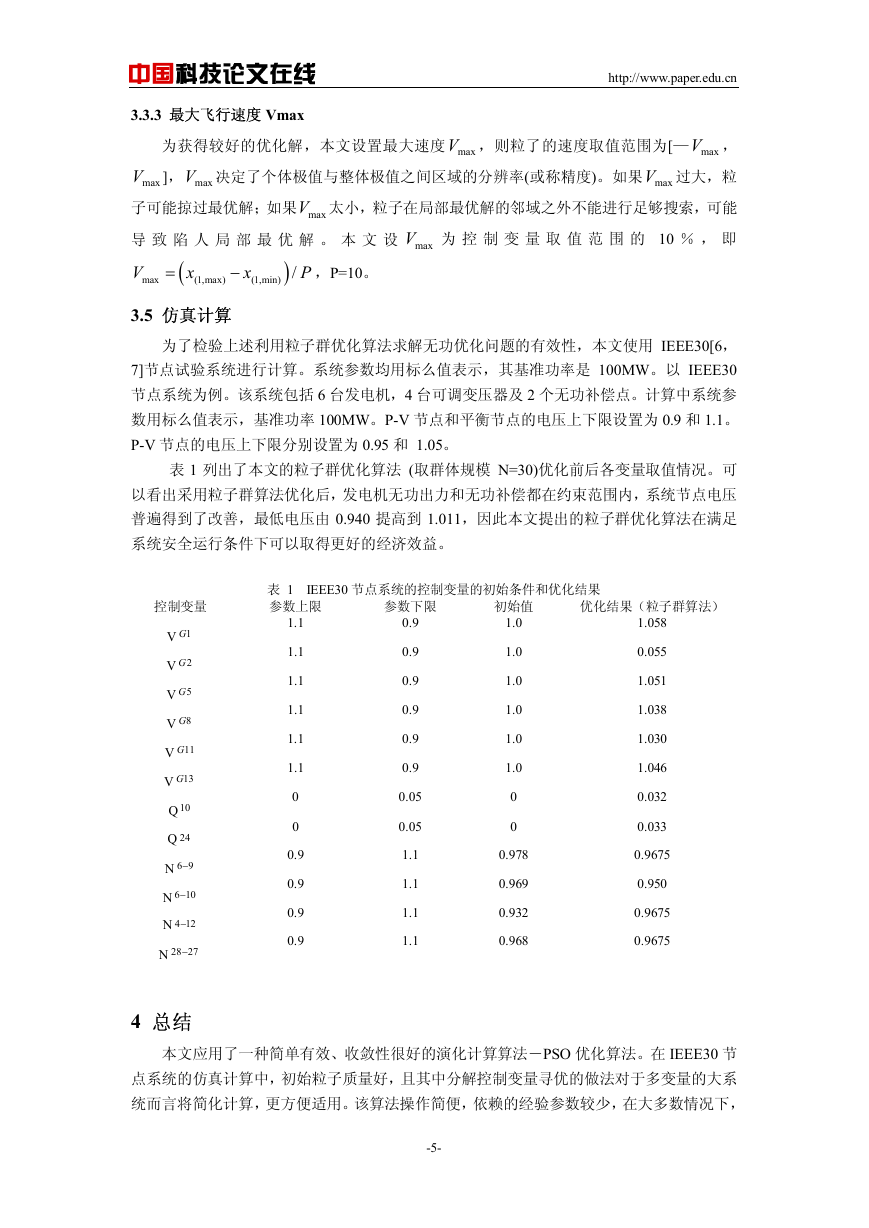表 1 列出了本文的粒子群优化算法 (取群体规模 N=30)优化前后各变量取值情况。可以看出采用粒子群算法优化后，发电机无功出力和无功补偿都在约束范围内，系统节点电压普遍得到了改善，最低电压由 0.940 提高到 1.011，因此本文提出的粒子群优化算法在满足系统安全运行条件下可以取得更好的经济效益。表 1 IEEE30 节点系统的控制变量的初始条件和优化结果参数上限参数下限 1.1 0.9 初始值 1.0 优化结果（粒子群算法） 1.058 1.1 1.1 1.1 1.1 1.1 0 0 0.9 0.9 0.9 0.9 0.9 0.9 0.9 0.9 0.9 0.05 0.05 1.1 1.1 1.1 1.1 1.0 1.0 1.0 1.0 1.0 0 0 0.978 0.969 0.932 0.968 0.055 1.051 1.038 1.030 1.046 0.032 0.033 0.9675 0.950 0.9675 0.9675 控制变量 V 1G V 2G V 5G V 8G V 11G V 13G Q 10 Q 24 N 96− 6− N 10 N 12 4− 28− 27 N 4 总结本文应用了一种简单有效、收敛性很好的演化计算算法―PSO 优化算法。在 IEEE30 节点系统的仿真计算中，初始粒子质量好，且其中分解控制变量寻优的做法对于多变量的大系统而言将简化计算，更方便适用。该算法操作简便，依赖的经验参数较少，在大多数情况下， -5-

中国科技论文在线 http://www.paper.edu.cn 可以收敛至满意解。与遗传算法相比较，其优势在于它没有较多参数需要调整，更加简单，容易实现且收敛速度快，用于求解无功优化问题是行之有效的。这种优化方法可以较好地协调算法的局部与全局搜索能力，有效地解决电力系统的无功优化问题，有利于提高配电网的无功优化水平。参考文献 [1]张文.基于粒子群优化算法的电力系统无功优化研究[D]. 济南：山东大学，2006. [2]袁晓辉，王乘，张勇传，袁艳斌.粒子群优化算法在电力系统中的应用[J].电网技术，2004,28（19）：14-19. [3] 姚煜，蔡燕春 . 离散粒子群与内点法结合的电力系统无功优化 [J]. 电力系统保护与控制 ,2010,38(3):48-52. Reactive Power Optimization Based on Partical Swarm Optimization Algorithm School of Information and Electrical Engineering, China University of Mining and Technology,Xuzhou Jiang su (221008) Li yinping Abstract Reactive power optimization is an effective measure to reduce power consumption. This paper introduces the Particle Swarm Optimization Algorithm with adaptive inertia weight factor and mutation operator to optimize the reactive power of power system .Furthermore using this method to calculate the reactive power optimization of the numerical example of IEEE 30-bus system. The results show that the optimization algorithm can be better coordinate search capability of local and global and effectively solve the problem of reactive power optimization. Key words:PSO algorithm;reactive power optimization;power system -6-

分享到：

赞收藏

资料库

基于粒子群优化算法的无功优化.pdf

相关推荐

开发技术

热门标签

最新资料