2019年陕西西安建筑科技大学运筹学考研真题.doc

发布时间：2022-09-21 发布人：admin 分类：说明书资料大小：0.08M 资料格式：doc 举报版权申诉

第1页 / 共4页

第2页 / 共4页

第3页 / 共4页

第4页 / 共4页

文本预览

2019 年陕西西安建筑科技大学运筹学考研真题一、单项选择题（每题 3 分，10 题，共 30 分） 1．可以通过（）来验证模型最优解。 A．观察 B．应用 C．实验 D．调查 2.线性规划模型不包括( )。 A．目标函数 B．约束条件 C．决策变量 D．状态变量 3.若线性规划问题没有可行解，可行解集是空集，则此问题( )。 A．没有无穷多最优解 B．没有最优解 C．有无界解 D．有无界解 4．线性规划灵敏度分析的主要功能是分析线性规划参数变化对（）的影响。 A．正则性 B．可行性 C．可行解 D．最优解 5．整数规划问题中，变量的取值可能是（）。 A．整数 B．0 或 1 C．大于零的非整数 D．以上三种都可能 6.运筹学运用数学方法分析与解决问题，以达到系统的最优目标。可以说这个过程是一个（）。 A．解决问题过程 B．分析问题过程 C．科学决策过程 D．前期预策过程 7. 若目标函数为求 max，一个基可行解比另一个基可行解更好的标志是（）。 A．使 Z 更大 B．使 Z 更小 C．绝对值更大 D．Z 绝对值更小 8.灵敏度分析研究的是线性规划模型中最优解和（）之间的变化和影响。 A．基 B．松弛变量 C．原始数据 D．条件系数 9．如果某种资源的影子价格大于其市场价格，则说明（）。 A．该资源过剩 B．该资源稀缺 C．企业应尽快处理该资源 D．企业应充分利用该资源，开僻新的生产途径

10．对偶单纯形法的迭代是从（）开始的。 A．正则解 B．最优解 C．可行解 D．基本解二、填空题（每空 2 分，7 个题，共 16 分） 1.1940 年 8 月，英国管理部门成立了一个跨学科的 11 人的运筹学小组，该小组简称为。 2. 数学模型中，“s·t”表示。 3．线性规划问题有可行解，则必有。 4.用大 M 法求目标函数为极大值的线性规划问题时，引入的人工变量在目标函数中的系数应为。 5.若线性规划的原问题为 maxZ=CX，Ax≤b，X≥0，则其对偶问题为。 6．在某生产规划问题的线性规划模型中，变量 xj 的目标系数 Cj 代表该变量所对应的产品的利润，则当某一非基变量的目标系数发生变化时，其有可能进入基底。 7.线性规划中，满足非负条件的基本解称为____，对应的基称为____。三、判断题（每题 2 分，7 题，共 14 分,错误用╳、正确用√） 1．图解法和单纯形法虽然求解的形式不同，但从几何上理解，两者是一致的（）。 2．线性规划模型中增加一个约束条件，可行域的范围一般将增大（）。 3. 对于动态规划问题，应用顺推或逆推解法可能会得出不同的最优解（）。 4. 如果一个线性规划问题有可行解，则一定有最优解（）。 5.一旦一个人工变量在迭代中变为非基变量后，该变量及相应列的数字可以从单纯形表中删除，而不影响计算结果（）。 6. 凡满足条件δ =C-CBB-1A≤0 的基 B 称为对偶可行基（）。 7. 若线性规划问题的可行域是无界的，则该问题可能存在：有限多个最优解（）。四、（15 分）用单纯刑法求解下列问题 max Z  2 x1  x2  3 x3  5x4 x  5 x  3 x  7 x  30  1 2 3 4

3 x1  x2  x3  x4  10 2 x  6 x  x  4 x  20  x  1  0, j 1, , 4 j 2 3 4 五、（15 分）对偶问题求解 3 2 已知线性规划 max Z  15 x1  20 x 2  5x3 x  5 x x  5  1 5 x1  6 x 2  x3  6 3 x 10 x 2  3 x  0, x 0, x  1 的最优解 X  (1 , 0, 19)T ，求对偶问题的最优解。  x  7 无约束 1 2 3 4 4 六、（10 分）由于某产品不但价格变化快而且更新快，某产品商尽量缩短订货周期，计划 10 天订货一次。某周期内该产品每台可获得进价 15％的利润，如果这期没有售完，则该产品商只能按进价的 90％出售并且可以售完。到了下一期产品商发现一种新产品上市了，价格上涨了 10％，他的利润率只有 10％，如果没有售完，则他可以按进价的 95％出售并且可以售完。假设市场需求量的概率不变。问产品商的订货量是否发生变化，为什么？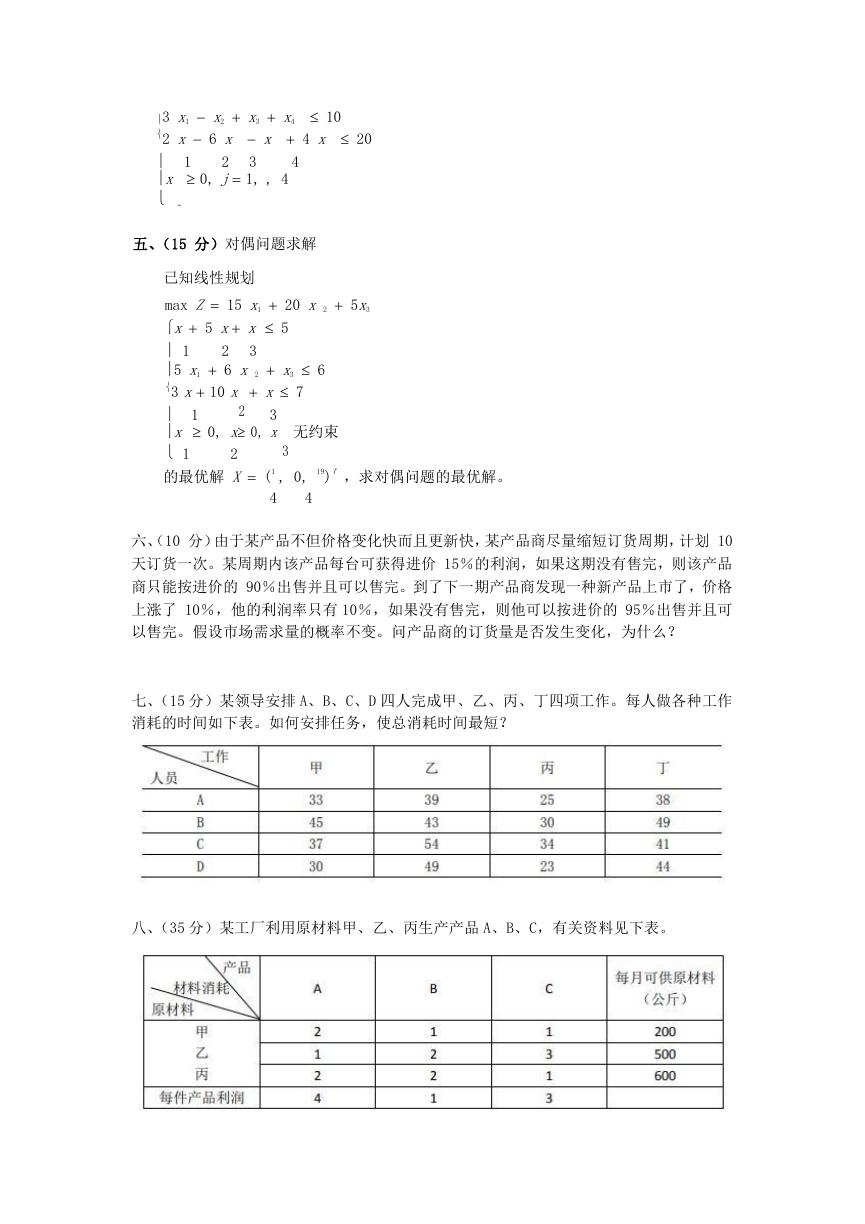七、（15 分）某领导安排 A、B、C、D 四人完成甲、乙、丙、丁四项工作。每人做各种工作消耗的时间如下表。如何安排任务，使总消耗时间最短？八、（35 分）某工厂利用原材料甲、乙、丙生产产品 A、B、C，有关资料见下表。

（1）怎样安排生产，使利润最大？（2）若增加 1 公斤原材料甲，总利润增加多少？（3）设原材料乙的市场价格为 1.2 元/公斤，若要转卖原材料乙，工厂应至少叫价多少，为什么？（4）单位产品利润分别在什么范围内变化时，原生产计划不变？（5）原材料分别单独在什么范围内波动时，仍只生产 A 和 C 两种产品？（6）由于市场的变化，产品 B、C 的单件利润变为 3 元和 2 元，这时应如何调整生产计划？（7）工厂计划生产新产品 D，每件产品 D 消耗原材料甲、乙、丙分别为 2 公斤，2 公斤及 1 公斤，每件产品 D 应获利多少时才有利于投产？

分享到：

赞收藏

资料库

2019年陕西西安建筑科技大学运筹学考研真题.doc

相关推荐

考研

热门标签

最新资料