logo资料库

机械臂关节空间 B 样条曲线轨迹规划.pdf

发布时间：2022-06-12 发布人：admin 分类：说明书 资料大小：0.17M 资料格式：pdf 举报 版权申诉
第1页 / 共6页
第2页 / 共6页
第3页 / 共6页
第4页 / 共6页
第5页 / 共6页
第6页 / 共6页
资料共6页，全文预览结束
    第 15 卷第 2 期 2000 年 6 月 安 徽 机 电 学 院 学 报 Jo urnal of A nhui I nsti tute of M e chanical ＆ Elec trical Eng inee ring V ol .15N o .2 Jun .2000 文章编号:1007-5240(2000)02-0021-06　 机械臂关节空间 B 样条曲线轨迹规划 王幼民 (安徽机电学院 机械工程系, 安徽 芜湖　241000) 摘　要:在关节空间使用 B 样 条曲 线对机 械臂 进行轨 迹规 划, 并与分 段 3 次 样条 曲 线进 行比 较, 用 B 样 条方法进行轨迹规划的具有分段处理性、 计算速度 快、 以及计算机内存占用 较少等 优点. 关键词:机械臂;B 样条函数;轨迹规划 中图分类号:TP241.2　　文献标识 码:A 前 　　言 机械臂的轨迹规划可分为在笛卡尔空间中和在关节空间中规划两种, 前者优点是概念 直观, 便于理解 , 但该方法涉及大量的笛卡尔空间与关节空间的大转称 , 求逆矩阵, 计算量 大 , 并且所用传感器不能直接测出机械臂在笛卡尔坐标系中的参数, 很难用于实时控制.由 于在笛卡尔坐标空间下轨迹规划的种种缺点, 使得面向关节空间的轨迹规划方法被广泛应 用 . 根据 Pual[ 1972] 提出的关节插值几点原则 , 最初有人提出了 4 —3 —4 轨迹, 3 —5 —3 轨 迹及 5 段 3 次轨迹等 .这种轨迹形成方法的优点是计算速度快, 易于处理操作机的动力约 束 , 可是当取样点落在拟合的光滑多项式曲线上时, 面向关节空间的笛卡尔路径会有所损 失.文献[ 1] 为斯坦福机器人解决了最短运行时间问题, 但这种方法不具有一般性 .文献 [ 2] 提出一种时间最短轨迹规划方法, 这种方法基于关节空间并考虑了各种最短路径、各种 实际约束, 但这种方法较复杂, 且只能离线完成 .文献[ 3] 、[ 4] 提出了各种机器人 CP 运动轨 迹的三次样条函数方法, 这种方法的优点是可得到优化的关节运动规律 , 但当中间路径点个 数 n 较多时 , 此法计算量大 , 且并未考虑机器人力矩约束.文献[ 4] 提出了一种机器人 CP 运 动轨迹规划算法 , 但这种算法经验性强, 所得到的结果是在做了大量简化的基础上得来的 , 可靠性较低 .文献[ 5] 给出了机械人 B 样条轨迹规划的矢量表达式及控制点的求法 , 但未给 出轨迹规划的边界条件, 未给出机器人 B 样条轨迹规划的局部支撑性. 本文推导出机械臂 B 样条轨迹的标量表达式, B 样条轨迹规划的边界条件 .为便于轨 迹优化 , 本文导出关节角速度 、加速角度的表达式 , 并论述了 B 样条的轨迹的局部支撑性. 所谓局部支撑性是指局部某段轨迹的速度或加速度超过机器人所允许的速度 、加速度的最 大值时 , 只需调整局部轨迹 , 符合要求的其它各段轨迹则不需变动 .本文用 pascal 语言编写 收稿日期:1999-11-24 作者简介:王幼民(1964 -), 男, 硕士, 助理研究员.
    · 22 · 安 徽 机 电 学 院 学 报 2000 年 出了 B 样条曲线形成机械臂轨迹的通用程序, 并在微机上通过 . 1 　B 样条轨迹规划方法 1.1 　等距 B 样条函数定义 　　　　　　 Bi , 1(u)= 1 , 　i ≤ u ≤ i +1 Bi , k(u)= u -i k -1 0 , 　其它处 Bi , k-1(u)+k -+i -u k -1 Bi+1, k-1(u) (1) 式中:k >1 ;i =0 , 1 , … , n -k ;u 为参数 .运用(1)式, 可推出各阶 B 样条的基函数. 当 k =4 时, 可求得四阶三次 B 样条基函数为: 1 -3 0 3 -6 -1 　　　　　　Bi , 4(u)= 1 3 ![ 1 　u 　u 2 　u 3] 0 3 -3 1 (2) 1 3 0 0 3 4 1.2 　四阶三次均匀 B 样条函数的推导方法 设函数的表达式(第 i 段)为: 　　　　θi(u)=X0(u)Vi-1 +X 1(u)Vi +X 2(u)Vi+1 +X 3(u)Vi +2 (3) 式(3)中, u 为参数, 0 ≤ u ≤1 ;X 1(u)为参数多项式, θi(u)表示第 i 段 B 样条曲线上 任意点的矢量 ;Vi -1, Vi , Vi +1 , Vi+2 为 B 样条曲线的一组控制点.由连续性的要求 , 相邻两段 B 样条曲线 θi(u)和 θi+1(u)分别在 u =0 和 u =1 处满足下面位置条件 : 　　　　　　　　　　θi(1)=θi+1(0). 将式(4)代入式(3), 整理后可得: 　X0(1)= X3(0)=0 , X 1(1)= X0(0), X2(1)= X1(0), X3(1)=X 2(0). 同样, 相邻两段曲线在连接点处连续的斜率和曲率, 应满足下面的连续性条件 , 即 : (4) (5) ﹒θi(1)=﹒θi +1(0),¨θ1(1)=¨θi +1(0). 由此可得到下面的 8 个条件, 包括 : ﹒X 0(1)=﹒X3(0)=0 , ﹒X 1(1)=﹒X 0(0), ﹒X 2(1)=﹒X1(0), ﹒X 3(1)= ¨X 2(0), ¨X 0(1)=¨X3(0)=0 , ¨X 1(1)=¨X 0(0), ¨X 2(1)=¨X1(0)=0 , ¨X 3(1)=¨X 2(0) 此外, 尚须满足柯西关系, 即坐标变换后不变性条件 : 　　　　　　　　X 0(u)+X 1(u)+X2(u)+X3(u)=1 (7) 假设 X(u)为三次多项式 , 由上述条件可求得三次多项式的全部系数.考虑到函数的对 (6) 称性, 可以假设: 　　　　X 0(u)=X 3(1 -u), 　　X 1(u)=X2(1 -u), 　　　　X 2(u)= a20u 3 +a 21u 2 +a 22 u +a23, X3(u)= a 30 u 3 +a 31 u 2 +a32 u +a 33. 由于 X0(1)= X3(0)=0 , ﹒X 0(1)= ﹒X3(0)=0 , ¨X 0(1)=¨X 3(0)=0. 因此可得:a 23 = a 30 , a 22 =3a 30 , a 21 =3a 30. 同样可以得 :a 31 =a32 =a 33 =0的关系 , 又根据(7)式, 考虑到对称性, 有 a20 =-3a 30 , a 30 =1/6 , 可求出 Xi(u)如下:
    第 2 期 王幼民 机械臂关节空间 B 样条曲线轨迹规划 · 23 · X 0(u)=(1 -u)3/ 6 , X 1(u)= u3/2 +2/3 -u 2 , X 2(u)=-u3/ 2 +u 2/ 2 +u/ 2 +1/ 6 , X3(u)= u 3/ 6. 1.3 　四阶三次 B 样条曲线的性质 平面四阶三次 B 样条曲线具有 C2 级连续, 三次 B 样条曲线的矢值方程为 : 　　　　　　　　θi(u)= ∑3 式(8)中 :i =1 , 2 , …, m -1 ;m 为关节空间的结点数 , V 为控制点 . 式(8)写成矩阵形式: Bj , 3(u)Vi+j-1 j =0 　　　　θi(u)=(1/6) 1 u u 2 u 3 1 4 1 -3 0 3 -6 -1 3 3 3 -3 0 0 0 1 Vi -1 Vi Vi +1 Vi +2 (8) (9) 式(9)中 i =1 , 2 , … , m -1. 四阶三次 B 样条曲线具有下列性质 : 性质一 :连续性.第 i 段B 样条曲线θi(u)(0 ≤u ≤1)的始点与终点的位置矢量分别为: θi(0)=(1/6)(Vi-1 +4Vi +Vi+1), θi(1)=(1/ 6)(Vi +4Vi +1 +Vi +2). 一阶段导数(连接处)和二阶导数连续, 因为B 样条曲线的一阶导矢和二阶导矢分别为: 　　　　θ′i(0)=(Vi+1 -Vi -1)/ 2 　θ′i(1)=(1/2)(Vi+1 -Vi-1), 　　　　θ″i(0)= Vi+1 -2Vi +Vi+1 　θ″i(1)= Vi +2Vi +1 -Vi +2. 由式(10)可以证明一阶、二阶导矢的连续性. (10) θ″i +1(0)= Vi -2Vi +1 +Vi+2 = θ″i(1);θ′i +1(0)=(Vi+2 -Vi)/ 2. 性质二:局部性 .三次 B 样条曲线各段仅由相邻的四个控制点确定, 因此变动特性多边 形的某个项点 , 只会影响与该顶点有关的相邻的四段曲线 , 其他地方的曲线不会引起变化 . 这一性质在机械臂轨迹优化时的表现为, 机械臂的整段轨迹可逐步优化, 这样就节省了优化 时间 , 有利于机械臂的实时控制. 1.4 　控制点的求法 (9)式中的 Vi-1 、Vi 、Vi +1、Vi+2 是一组控制点, 在机械臂轨迹规划中 , 往往先知其所求轨 迹上的型值点 , 型值点即经机械臂运动学逆问题求解求出来的结点.要对给定的型值点进 行轨迹规划, 就必须先求控制点.设 P 为关节空间的型值点 , 由下列条件: 　　　　θi -1(1)= θi(0)= Pi 　(i =1 , 2 , …, m -1) (11) 而 　　　θi-1(1)=θi(0)=(1/ 6)(Vi -1 +4Vi +Vi +1) (12) 式(12)中 m +2个未知 数 , 但只有 m 个方程 , 因此 要补充两个条件 , 即所谓的 边界条 件.各种边界条件的讨论见后 , 这里不妨取重节点条件 , V1 = V0 , Vm+1 = Vm. 6 -6 4 1 1 　　　　　　 1 4 1 V0 V1 V2 =6 1 4 1 6 -6 Vm Vm+1 0 P1 P2 Pm 0 (13)
    · 24 · 安 徽 机 电 学 院 学 报 2000 年 　　方程(13)可以唯一确定一组 V0、V1 、V2 、…… 、Vm 、Vm+1.由 Vi-1 、Vi 、Vi +1 +Vi +2 确定的 B 样条曲线为 : 　　　　θi(u)=(1/6) u3 u2 u 1 3 -3 1 0 3 -1 3 -6 -3 0 1 4 3 1 0 0 Vi+2 Vi-1 Vi Vi +1 (14) 3u 3 -3u +1)Vi+1 + 1 6 u3 Vi +2　　　(u 为参数 　0 ≤ u ≤1) θi(u)=(1/6)(-u 3 +3u 2 -3u +1)Vi -1 +(1/ 6)(-u 3 +6u 2 +4)Vi +(1/6)(-3u3 + (15) 设关节空间有一系列型值点 P1 、P2 、…… 、Pm , 由方程(13)可求出 m +2 个控制点 V0 、 V1 、V2 、… …、Vm 、Vm+1 , 每相邻的两点之间可用一条 B 样条曲线将其连接, 整个轨迹由 m -1 段 B 样条曲线拼接而成, 设第 i 段 B 样条曲线连接 Pi 、Pi+1 两点 , 第 i 段曲线由Vi -1 、Vi 、Vi+1 、 Vi +2 四个控制点控制, 设这 4 个控制点的坐标为 :Vi -1(ti-1 , qi -1)、Vi(ti , qi)、Vi +1(ti +1, q i+1)、 Vi +2(ti +2, q i+2). 第 i 段 B 样条曲线为式(14).式中, u 为参数 , θi(u)为曲线上的点, 参数 u 遍取 0 到 1 之 间之值 , 就可得到第 i 段曲线.第 i 段曲线上任意点的横、纵坐标分别用 t(u)、q(u)表示 . 　　t(u)=(1/ 6) u 3 u 2 u 1 　　q(u)=(1/6) u3 u2 u 1 1.5 　边界条件 0 1 3 1 3 -3 3 -1 3 -6 -3 0 0 4 1 0 -1 3 -3 1 3 -6 0 -3 0 0 1 3 3 4 1 0 t i-1 ti t i+1 t i+2 qi-1 qi qi+1 qi+2 (16) (17) 为了求 V0 、Vm+1 , B 样条轨迹规划需要附加 2 个边界条件, B样条方法边界条件表现为确 由(14)式两边同时对参数 u 求导, 得到轨迹的一阶导矢和二阶导矢, 它们分别用符号 定附加控制点 V0 及 Vm+1. ω(u), ε(u)表示 : ωi(u)= d du θi(u)=(1/ 6)(-3u2 +6u -3)Vi -1 +(1/ 6)(9u 2 -12u)Vi + (1/ 6)(-9u2 +6u +3)Vi +1 +u2 V1+2/2 ωi(u)=(1/6)(-6u 2 +6)Vi-1 + εi(u)= d du (1/ 6)(18u -12)Vi +(1/6)(-18u +6)Vi+1 +uVi +2 　　　　　　ωi(u)=dθi(u) (20)式中 t′ dt(u) = dt(u) , , q′ dq(u) du ) d u d u du dq(u) du =[ t , q] (18) (19) (20)
    第 2 期 王幼民 机械臂关节空间 B 样条曲线轨迹规划 　　　　　　εi(u)=d ωi(u) =[ dt′ , dq′ ] =[ t″, q″] du du du , q″= dq′ . du · 25 · (21) (21)式中 :t″=dt′ du 速度的表达式为: 　　　　　　　　　　　　﹒θi(u)= q′/ t′ 加速度表达式为: 　　　　　　¨θi(u)= d﹒θ(u) (23) 由速度、加速度的表达式可知 , 当关节角的一阶导矢为伪零时, 关节速度为零;当关节角 的二阶导矢为零时 , 关节加速度为零.关节角一阶导矢为伪零是指一阶导矢的第一个分量 不为零, 其余分量为零, 这一矢量 Ψ定义为(1 , 0). = q″t′-q′t″ = d﹒θi(u) (22) du dt t′3 du dt 1)起点 、终点的速度为零. 　　ω1(0)=(1/6)(-3)V0 +(1/ 2)V2 = Ψ　∴V0 = V2 -2 Ψ 　　ω1(1)=(1/6)(-3 +6 -3)Vm-2 +(1/6)(9 -12)Vm-1 +(1/ 2)Vm+1 = Ψ ∴　Vm+1 =2 Ψ+Vm-1. 2)起点 , 终点的加速度为零. 　　ε1(0)= V0 -2V1 +V2 =0 , 　∴V0 =2V1 -V2. 　　εm+1(1)= Vm-1 -2Vm +Vm+1 =0 , 　∴Vm+1 =2Vm -Vm-1. 3)起点的速度为零 , 终点的加速度为零.用上述方法可求得边界条件为: V0 = V2 -2 Ψ, 　　Vm+1 =2Vm -Vm-1. 4)起点的加速度为零, 终点的速度为零. V0 =2V1 -V2 , 　　Vm+1 =2 Ψ+Vm-1. 5)重结点.有些边界条件为重结点 , 重结点的条件为: V0 = V1 , 　　Vm+1 = Vm. 其他边界条件可用同样的方法推导. 2　轨迹规划算例 当机械臂末端(手)在笛卡尔空间中从一点运动 到另一点(直线或曲线运动), 其始点及轨迹中的中间 点通过机器人运动学逆问题求得各关节空间中的型 值点 , 关节空间的型值点可通过文献[ 6] 的方法求出 . 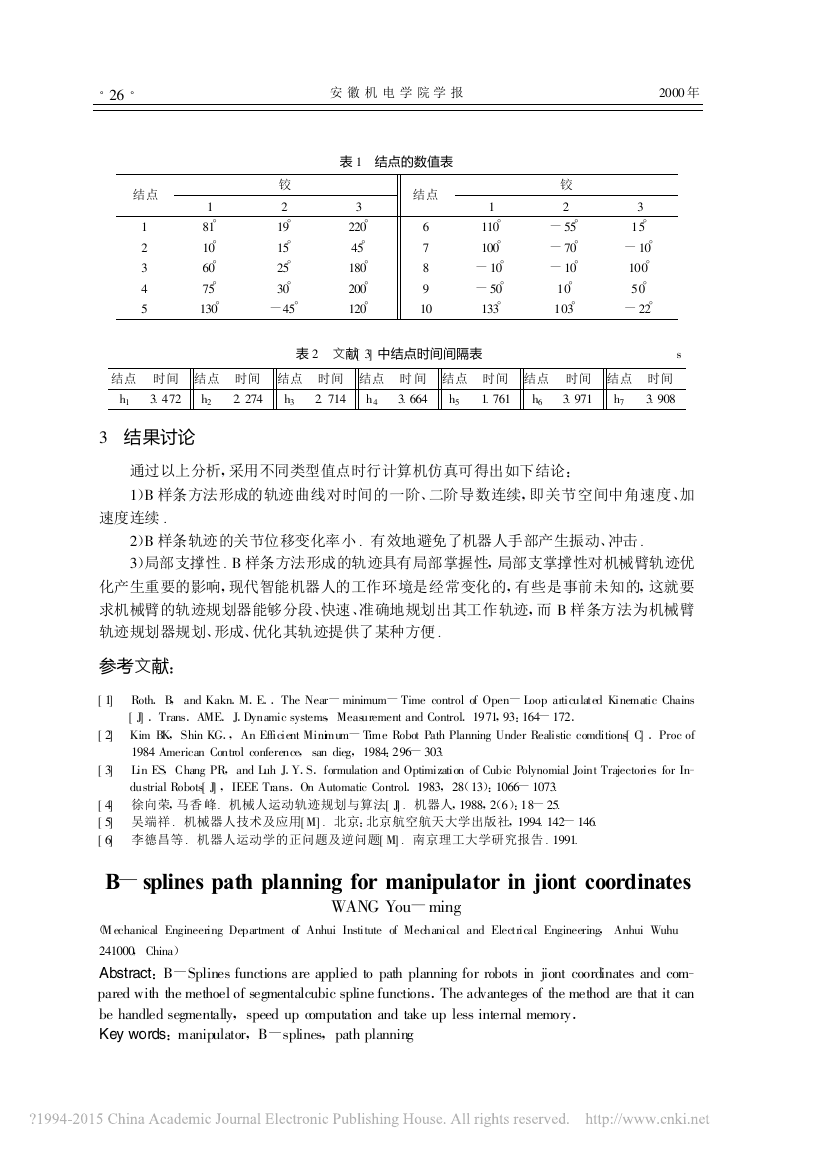本文以 Puma560 机器人为例 , 引用文献[ 3] 中的算例 的原始数据对 Puma560 机器的前三铰进行了 B 样条 轨迹规划 , 文献[ 3] 中的原始数据如表 1 , 各结点间的 时间间隔见表 2 , 其中 ti -ti -1 = hi -2(i =3 …9).各 铰轨迹曲线见图 1. 表 1 中 , 结点 1 与结点 10 为附加结点 , 是根据初 始条件、边界条件求出的 , 边界条件为 V2 = Vo =0 . 图 1　各关节铰 B 样条轨迹规划图
    · 26 · 安 徽 机 电 学 院 学 报 2000 年 结点 1 2 3 4 5 1 81° 10° 60° 75° 130° 表 1　结点的数值表 3 220° 45° 180° 200° 120° 结点 6 7 8 9 10 1 110° 100° -10° -50° 133° 铰 2 19° 15° 25° 30° -45° 铰 2 -55° -70° -10° 10° 103° 3 15° -10° 100° 50° -22° 表 2 　文献[ 3] 中结点时间间隔表 s 结点 时间 结点 时间 结点 时间 结点 时 间 结点 时间 结点 时间 结点 时间 3.908 3.472 2.714 3.664 2.274 h 4 h1 h5 1.761 h6 3.971 h7 h2 h3 3　结果讨论 通过以上分析 , 采用不同类型值点时行计算机仿真可得出如下结论 : 1)B 样条方法形成的轨迹曲线对时间的一阶、二阶导数连续 , 即关节空间中角速度 、加 速度连续 . 2)B 样条轨迹的关节位移变化率小.有效地避免了机器人手部产生振动、冲击. 3)局部支撑性.B 样条方法形成的轨迹具有局部掌握性, 局部支掌撑性对机械臂轨迹优 化产生重要的影响 , 现代智能机器人的工作环境是经常变化的 , 有些是事前未知的, 这就要 求机械臂的轨迹规划器能够分段 、快速 、准确地规划出其工作轨迹 , 而 B 样条方法为机械臂 轨迹规划器规划、形成、优化其轨迹提供了某种方便. 参考文献 : [ 1] 　Roth.B, and Kakn.M.E..The Near -minimum -Time control of Open -Loop articulated Kinematic Chains [ J] .Trans .AME.J.Dynamic systems, Measurement and Control.1971, 93 :164-172 . [ 2] 　Kim BK, Shin KG., An Efficient Minimum -Time Robot Path Planning Under Realistic comditions[ C] .Proc of 1984 American Control conference, san dieg , 1984:296-303. [ 3] 　Lin ES, Chang PR, and Luh J.Y.S .formulation and Optimization of Cubic Polynomial Joint Trajectories for In- dustrial Robots[ J] , IEEE Trans .On Automatic Control.1983 , 28(13):1066-1073. [ 4] 　徐向荣, 马香 峰.机械人运动轨迹规划与算法[ J] .机器人, 1988 , 2(6):18-25. [ 5] 　吴端祥.机械器人技术及应用[ M] .北京:北京航空航天大学出版社, 1994.142-146. [ 6] 　李德昌等.机器人运动学的正问题及逆问题[ M] .南京理工大学研究报告.1991. B-splines path planning for manipulator in jiont coordinates WANG You -ming (M echanical Engineering Department of Anhui Institute of Mechanical and Electrical Engineering, Anhui Wuhu 　 241000, China) Abstract :B -Splines functions are applied to path planning for robots in jiont coordinates and com- pared with the methoel of segmentalcubic spline functions .The advanteges of the method are that it can be handled segmentally , speed up computation and take up less internal memory . Key words :manipulator , B -splines , path planning
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料