第1页 / 共13页
第2页 / 共13页
第3页 / 共13页
第4页 / 共13页
第5页 / 共13页
第6页 / 共13页
第7页 / 共13页
第8页 / 共13页
元自步学习（综述论文）.pdf
中国科学 : 信息科学 2020 年 第 50 卷 第 6 期 : 781–793
SCIENTIA SINICA Informationis
大数据分析专题 . 论文
元自步学习
束俊1, 孟德宇1,2*, 徐宗本1
1. 西安交通大学数学与统计学院, 西安 710049
2. 澳门科技大学澳门系统工程研究所, 澳门 999078
* 通信作者. E-mail: dymeng@mail.xjtu.edu.cn
收稿日期: 2020–01–06; 接受日期: 2020–03–01; 网络出版日期: 2020–06–10
国家自然科学基金 (批准号: 61661166011, 11690011, 61603292, 61721002, U1811461) 资助项目
摘要 自步学习是近年来机器学习领域提出的一种启发于人和动物 “由易到难” 学习过程的学习机
制. 尽管自步学习已取得可喜的理论与应用进展, 但是当前的自步学习算法仍存在超参数选择的瓶颈
问题. 针对该问题当前主要采用一些启发式的手工设计方法或者交叉验证方法, 然而此类方法效率很
低, 缺乏理论性指导, 难以推广应用到广泛的实践问题中. 针对这一挑战性问题, 本文提出一种基于元
学习机理的自步学习算法, 该方法能使自步学习中涉及的超参数以数据驱动的方式自动习得, 从而大
大减弱了自步学习的这一核心问题. 特别地, 我们针对 3 种典型的自步学习实现格式, 将所提元学习
策略实质性嵌入, 通过回归和分类实验验证了所提算法的准确性和泛化性, 特别验证了相比于传统超
参设置方法的显著优越性.
关键词 自步学习, 元学习, 样本加权, 噪声标记下学习, 超参数选择
1 引言
课程学习 [1] 尝试模拟一般生物通常采用的 “从易到难” 学习机制, 其执行模式为预先将数据按照
某种预设 “课程” 从易到难排序, 然后按此顺序将数据逐步输入学习模型进行增量式学习. 近年来, 课
程学习策略被广泛应用于弱监督学习 [2]、多任务学习 [3, 4]、迁移学习 [5]、多模态学习 [6]、自然语言理
解 [7] 等. 课程学习方法论因而逐渐引起机器学习领域更多的研究关注, 成为较为热点的研究课题.
虽然课程学习在一些应用中体现出良好的性能, 但其性能依赖于预先主观制定的课程质量, 这需
要用户对领域拥有足够全面的先验知识. 对于现实中常见的缺乏充分领域先验认知的应用领域, 课程
学习的有效执行仍面临着很大困难. 为了克服课程学习中自适应课程设置问题, 自步学习 [8] 提出将课
程难易的度量准则嵌入到优化模型当中, 一边基于当前样本排序更新模型参数, 一边基于学习的效果
对所有样本更新这一度量从而获得样本的新一轮难易排序, 最终达到自动化更新课程、自适应样本排
序的目的.
引用格式: 束俊, 孟德宇, 徐宗本. 元自步学习. 中国科学: 信息科学, 2020, 50: 781{793, doi: 10.1360/SSI-2020-0005
Shu J, Meng D Y, Xu Z B. Meta self-paced learning (in Chinese). Sci Sin Inform, 2020, 50: 781{793, doi: 10.1360/
SSI-2020-0005
c⃝ 2020 《中国科学》杂志社
www.scichina.com infocn.scichina.com
束俊等: 元自步学习
考虑一个标准的监督学习问题: 给定训练数据集 D = {xi, yi}N
i=1, 其中 xi ∈ X 代表样本 (X 表
示样本空间), yi ∈ Y 代表标记 (Y 表示标记空间), N 是所有样本的数目. 如果 Y 是连续的, 该问题
为回归问题; 若 Y 是离散的, 该问题为分类问题. 机器学习的目标是学习一个预测函数 fw : X → Y ,
w ∈ Γ, 其中 w 为预测函数的参数. 获得此决策函数后, 我们即可对任意新样本进行预测. 该问题的求
解一般需要构建如下的优化模型:
LTrain(fw(xi), yi) + R(w),
(1)
其中 LTrain(·,·) 为训练数据集上的损失/误差项, 其作用在于度量预测与真实标记之间的差异程度, 常
用的误差形式包括交叉熵损失 (分类)、均方误差 (回归) 等; R(w) 为正则项, 其作用在于编码需要求
解 w 的预知先验信息.
自步学习的基本执行模式为: 在传统机器学习模型 (1) 中, 通过嵌入衡量每个样本难易程度或对
学习目标重要性进行刻画的权重变量 vi, 通过求解如下优化问题实现对该参数与模型参数 w 的共同
优化, 从而达到样本课程与学习模型共同学习的目的 [8]:
(viLTrain(fw(xi), yi) + g(vi, λ)) ,
(2)
N∑
min
w2
i=1
N∑
min
w2,v2[0,1]N
i=1
其中 λ 是年龄参数, g(v, λ) 是自步正则, 用于编码自步学习由易到难的学习模式, 其定义及需要满足
的条件可以参见文献 [9, 10], 详细阐述见第 3 部分. 由于 R(w) 对分析自步正则没有本质影响, 故在下
文中省略该项. 在之后的介绍中, 为了简化符号表示, 我们也常常将第 i 个样本的误差 L(fw(xi), yi) 简
记为 ℓi.
求解问题 (2) 可以采用交替迭代算法对参数 w 和 v 进行更新, 具体如下.
步骤 1. 固定参数 w
, 求解 v, 即求解如下问题:
i = arg min
v
v2[0,1]
viLTrain(fw (xi), yi) + g(vi, λ),
i = 1, 2, . . . , n.
步骤 2. 固定参数 v
, 求解 w, 即求解如下问题:
w
= arg min
w
i=1
v
i
LTrain(fw(xi), yi).
(3)
(4)
N∑
∫
步骤 3. 更新完 v 与 w, 增加 λ 的值, 使更多样本进入学习过程.
完整算法如算法 1 所示. 在算法的不断迭代过程中, 会将误差较大的标记数据作为不可靠性样本
通过设置较小甚至零权重的方式将其在训练过程中的作用减弱甚至消除, 从而减小或者避免了此类样
本对于分类器学习的负面影响. 进一步地, 可以证明, 在自步学习迭代优化样本权重与分类器参数的执
行过程中, 其实存在一个以分类器参数为变量的隐藏目标函数 Fλ(ℓ), 也在同步单调下降 [11], 其定义为
Fλ(ℓ) =
ℓ
v
0
(ℓ; λ)dℓ.
(5)
这一隐藏目标函数能够更为本质地说明自步学习这种算法模式的稳健性本质 [11], 如图 1 所示.
782
中国科学 : 信息科学 第 50 卷 第 6 期
图 1 (网络版彩图) 元自步学习在学习过程中的隐式损失函数变化. (a) 和 (b) 分别展示回归和分类实验上的实验
结果
Figure 1 (Color online) Variations of learned latent loss functions during learning process. (a) and (b) show the results
of regression and classification experiments, respectively
算法 1 自步学习求解算法
输入: 数据 fxi; yigN
输出: 模型参数 w;
初始化: w0; v0; 0; t = 0;
1: if t < T then
i=1, 最大迭代次数 T , 批样本数 n;
t = t + 1;
2:
3: 求解 (3) 更新 v(t);
4: 求解 (4) 更新 w(t);
5: 增加 ;
6: end if
注意到算法中变量 v 和 w 的优化均可保证目标函数 (2) 的单调下降, 而 λ 的更新是基于由易到
难的课程学习模式启发式制定的, 对其更新并不能保证目标函数 (2) 的递减性 (事实上, 往往反而导
致该目标的递增效果). Meng 等 [11] 指出, 在学习的后期阶段, 随着年龄参数的逐步增大, 异常值或者
无意义的噪声样本会参与到训练过程中, 从而对模型学习效果产生损害. 针对这一问题, 文献中一般
采用 “中间截停” 策略终止算法, 而选取终止的 λ 参数可以通过验证集的验证策略进行估计 [9]. 另一
方面, 年龄参数 λ 在每一次迭代之后采用何种机制上升, 也是需要谨慎思考的问题. 如果将其设置的
初值过大或增速过快, 则可能进入学习的训练样本过快过多, 从而导致无法充分执行课程学习从易到
难的逐步学习模式, 也可能导致噪声或异常样本在学习过程中的过早侵入, 从而产生训练效果的偏差;
而如果将其设置的初值过小或增速过慢, 则可能进入样本过少, 导致算法学习速度过慢. 更为严重的
是, 随着迭代次数的进行, 模型学习越来越准确, 导致所有样本的损失整体下降, 此时 λ 有可能并非要
增大, 反而需要逐步减小. 为了克服这一超参数选择问题, Meng 等 [11] 提出一种启发式的设定参数 λ
的方法, 即将 λ 选择转换为样本个数的选择, 通过逐次增加样本进入的个数, 使得课程参数的选择更
加直观. 但是为了有效控制进入样本的个数变化, 往往需要了解数据更多的先验知识, 否则算法的鲁
棒性和可重复性往往难以保证. 该超参数 (即年龄参数 λ) 的合理设定问题已成为自步学习面向真实
应用的瓶颈问题.
为了解决上述问题, 本文提出一种新型的元自步学习算法. 该算法能够将改善年龄参数与优化模
型参数放置于同一个优化框架中, 从而实现从数据中动态调节年龄参数的学习效果. 我们将 3 种经典
的自步学习实现格式嵌入到所提的元学习算法中, 针对其构建了超参数的自动学习策略. 通过回归和
分类实验, 验证了所提元学习算法相比于传统方法更优的学习效果, 从而说明了所提算法的有效性.
783
Latent Meta-Linear loss during learning processMeta-Linear under different noise ratio1086420Loss543210Loss−3−2−10123−3−5−4−2−1012345y−f (x)y·f (x)LS lossMeta-Linear step 1Meta-Linear step 50Meta-Linear step 100Zero-one lossCross entropyLinearMeta-Linear-20%Meta-Linear-40%Meta-Linear-60%(a)(b)
束俊等: 元自步学习
本文组织结构如下: 第 1 节介绍了自步学习及其年龄参数设定目前存在的问题, 第 2 节回顾自步
学习及其超参数学习的相关工作, 第 3 节构建针对自步学习超参数自动选择的元学习算法, 并在 3 种
典型的自步学习实现格式中本质嵌入, 第 4 节通过实验分析论证了所提算法的有效性, 第 5 节对本文
进行了总结.
2 相关工作简介
2.1 自步学习
2009 年, Bengio 等 [1] 首次提出了课程学习的概念. 其基本思想是通过组织训练样本从易到难逐
步地输入学习模型, 从而达到良好的运算效果. 针对其课程标准自动化设置问题, 2010 年出现了自步
学习 [8] 的思想方法, 提出把用以课程排序的难易度量嵌入到优化模型, 自动学习该度量的基本策略.
由于该类学习方法论的一般性和广泛适用性, 自步学习被广泛用于不同的任务, 如多媒体事件检测 [9]、
显著性检测 [12]、物体检测 [13]、图片分类 [14]、物体追踪 [15] 等, 并获得了良好的应用效果. 自步学习的
本质也不断从深度和广度方面被推进. 例如, Jiang 等 [14] 提出了自步课程学习, 通过老师 – 学生共同
的教学 – 学习功能实现从易到难的课程学习目标. Meng 等 [11] 证明了自步学习的迭代优化算法完全
对应于一个鲁棒损失函数的 majorization-minimization (MM) 求解算法的迭代过程, 并在此后深入证
明了自步学习收敛性的结论 [16]. 这项工作揭示了自步学习具有鲁棒学习的本质内涵. 进一步地, Liu
等 [17] 阐明了自步学习模型与凹共轭形式的本质等价性, 并在此框架下, 诱导出更多一般形式的自步
正则. 然而, 所有这些工作都未能对自步学习的超参数选择提供理论较为完善、具有广泛适用性的一
般算法.
2.2 超参数优化
超参数优化试图针对一个优化模型的超参数进行自适应选择或学习, 从而使其获得良好的推广应
用性能. 典型的超参数选择方法包含网格搜索、随机搜索 [18]、贝叶斯 (Bayes) 优化 [19]、交叉验证 [20]
等. 最近, 基于元学习的超参数优化 [1921] 逐步引起关注并被普遍尝试使用. 例如, 基于元学习的策
略, 针对样本权值这一复杂超参数出现了多种数据驱动学习策略 [2224]. 实验验证了这种自适应的元
学习策略的确能够有益于增强原始优化问题对于复杂数据偏差的鲁棒性与准确性. 本文可以视为该方
法论在自适应学习自步学习的年龄参数的探索.
3 元自步学习
3.1 典型的自步学习算法
自步学习模型 (2) 中, 自步正则 g(v, λ) 旨在诱导出一个从易到难的学习模式, 其严格数学化定
义 [9, 10] 如下.
定义1 (自步正则) 对于优化模型 (2), 当 g(v, λ) 满足以下条件时, 称之为一个自步正则项:
(1) g(v, λ) 关于其变量 v ∈ [0, 1] 为凸函数;
(2) v
(ℓ, λ) 为变量 ℓ 的单调递减函数, 且成立 limℓ!0 v
(ℓ, λ) 为变量 λ 的单调递增函数, 且成立 limλ!0 v
(ℓ, λ) = 1, limℓ!1 v
(ℓ, λ) = 0, limλ!1 v
(ℓ, λ) = 0;
(ℓ, λ) 6 1;
(ℓ, λ) = arg minv2[0,1] vℓ + f (v, λ).
(3) v
其中 v
784
基于上述定义, 我们可以构造出很多体现数据内涵的自步正则格式. 这里我们给出 3 个典型的自
中国科学 : 信息科学 第 50 卷 第 6 期
0, if ℓ > λ,
1, if ℓ < λ,
−ℓ/λ + 1, if ℓ < λ,
1,
(
(
if ℓ > λ,
if ℓ <
if ℓ > λ2,
(λ; ℓ) =
)
0,
0,
− 1
λ
1p
ℓ
γ
, otherwise,
λγ
λ+γ
)2
,
(6)
(7)
(8)
步正则格式及其对应的权值求解公式, 如下:
f H (v; λ) = −λv,
(
f L(v; λ) = λ
v
(λ; ℓ) =
)
v2 − v
1
2
,
v
f M (v; λ) =
γ2
v + γ/λ
v
,
(λ, γ; ℓ) =
其中 λ, γ 表示需要设置的超参数, 统一记为 Λ.
以上自步正则项分别构造于文献 [8∼10] 中, 分别称为 Hard, Linear 和 Mixture 自步正则. 从上述
权重求解公式可以看出, 当一个样本在当前模型参数下, 对应误差 ℓ 比年龄参数 λ 或者 λ2 大时, 对应
样本倾向于被认为是相对可靠性较低的难训练噪声样本, 其对应权重为 0, 其作用为消除这些样本对
训练过程产生的影响; 反之, 对应误差 ℓ 比年龄参数 λ 或者 λ2 小时, 这样的样本可被认为是分类可靠
性较高的易训练相对纯净样本. 相比这些自步正则的加权格式, Hard 自步正则对每个样本要求选或者
不选 (即 “硬” 加权), 而 Linear 自步正则形式赋予每个样本 “软” 加权以更为客观准确地反映样本的
重要性程度, 而 Mixture 自步正则能够结合二者的优势, 对非常重要的一批样本赋予权重 1, 又对误差
较小的样本赋予软加权, 从而有望能够更为充分体现样本重要性, 获得更好的学习效果.
3.2 元自步学习算法
正如第 1 节所述, 如何选取合适的年龄参数是影响自步学习学习效果及增强其可复现性的关键因
素. 受当前元学习技术 [2429] 的启发, 本文提出元自步学习方法, 旨在实现自适应调整自步学习超参
数的功能.
具体地, 当我们在训练集 D 上优化自步学习目标函数 (2) 时, 因为训练数据集的分布形式 (即干
净样本和噪声样本的分布) 未知, 传统的若干启发式解决方案, 特别是使用验证集进行参数评估验证
的策略, 在现实的应用中存在诸多困难. 例如, 验证集该如何选择和充分利用, 自步学习迭代中止标准
如何设定, 自步学习年龄参数该如何动态变化等. 为了克服这些问题, 元学习方法的基本思路为, 将传
统验证集的收集标准提高, 对其质量进行严格要求, 从而保证其能够较为合理地体现数据背后真实分
布的形态. 在这样的要求下, 该验证集就构成能够对训练数据进行良态引导的元数据集, 其一方面具
有较小的量, 而另一方面对于问题相比训练数据具有更高的可靠性 [2224].
具体方法步骤如下. 预先收集少量的元数据 (干净样本) Dmeta = {x(m)
}M
i=1, 通过在元数据
集上的损失指导年龄参数的学习, 如下式所示, 其中 M 是元样本的个数, 且 M ≪ N :
, y(m)
i
i
)
Λ
其中,
= arg min
fw()(x(m)
i
), y(m)
i
,
w(Λ) = arg min
w
i=1
(viL(fw(xi), yi) + g(vi, Λ)) ,
(
L
M∑
N∑
i=1
(9)
(10)
785
束俊等: 元自步学习
其中 L 表示在训练数据上的损失函数, 本文在分类问题上用交叉熵误差, 回归问题上用均方误差.
因此, 元自步学习算法所优化的是一个双边优化问题 [25, 30], 其中外目标函数是问题 (9), 内目标
函数是问题 (2). 由于该问题很难获得准确结果, 借助文献 [23, 24] 中采用的技术, 我们采取如下在线
近似策略联合交替更新年龄参数集 Λ, 权重 v 和模型参数 w.
步骤 1. 固定参数 w
, 求解 Λ, 即优化目标函数 (9). 这里基于上一步的模型参数 w(t1) 和超参
数 Λ(t1), 采用随机梯度下降方法在 Dmeta 上选取 m 个批样本求解, 即
Λ(t) = Λ(t1) − β
f ^w(t)()(x(m)
i
), y(m)
i
,
(t1)
(11)
其中 ˆw(t)(Λ) 的形式通过在 D 上选取 n 个批样本按如下方式构建:
ˆw(t)(Λ) = w(t1) − α
∇wvi(Λ)LTrain(fw(xi), yi),
α, β 是随机梯度下降算法的学习率.
步骤 2. 基于上一步的模型参数 w(t1) 和更新获得的超参数 Λ(t), 求解 v:
i=1
v(t)
i = arg min
v2[0,1]
viLTrain(fw(t1) (xi), yi) + g(vi, Λ(t)),
i = 1, 2, . . . , n.
(12)
针对我们选取的 3 种典型自步学习算法, 当模型参数 w 固定后, 均具有闭式解形式. 此时只需要将 Λ(t)
带入式 (6) 中的权重求解公式, 即可得到 v(t).
步骤 3. 基于得到的 v(t), 求解 w(t). 采用随机梯度下降方法, 在 D 上选取 m 个批样本进行求
m∑
i=1
(
∇
n∑
)
解, 即
w(t)(Λ) = w(t1) − α
n∑
i=1
∇wv(t)
i
LTrain(fw(xi), yi)
.
w(t1)
(13)
完整元自步学习算法如算法 2 所示. 可以看出, 相比于原自步学习算法, 该算法通过元数据指导超参
数 Λ 进行自适应的调整和学习. 这一算法可以很方便整合到任何分类或者回归模型当中, 因而具有一
般的可用性. 特别地, 当自步正则采取 (6) 的 Hard, Linear 和 Mixture 形式时, 记对应的元自步学习算
法分别为 Meta-Hard, Meta-Linear 和 Meta-Mixture.
i=1, 元数据集 fx(m)
i
算法 2 元自步学习求解算法
输入: 数据 fxi; yigN
输出: 模型参数 w;
初始化: w0; v0; Λ0; t = 0;
1: if t < T then
; y(m)
i
gM
i=1, 最大迭代次数 T , 批样本数 n 和 m;
t = t + 1;
2:
3: 求解 (11) 更新 Λ(t);
4: 求解 (12) 更新 v(t);
5: 求解 (13) 更新 w(t);
6: end if
4 实验结果
本节将通过仿真回归实验和 CIFAR-10, CIFAR-100 数据集上的分类实验验证所提元自步学习算
法的有效性.
786
中国科学 : 信息科学 第 50 卷 第 6 期
表 1 仿真回归实验中各对比方法性能比较 (LS 误差)
Table 1 Performance comparison (LS error) on simulation experiment of all compared methods
Methods
LS
Test error
86.23
Hard
3.26
Meta-Hard
Linear
Meta-Linear
Mixture
Meta-Mixture
2.32
2.40
1.56
1.87
1.35
4.1 仿真回归实验
我们采用文献 [11] 中的实验设计生成仿真数据. 该数据集包含 1000 个数据点, 通过以下分布
生成:
其中,
3∑
i=1
πipi(X, Y ) = p(X)pi(Y |X),
p(X) = U (Ω1), Ω1 = {x|x ∈ [−1, 1]},
π1 = 0.3,
p1(Y |X) = N (f (X), 1),
p2(Y |X) = Laplacian(f (X), 1),
p3(Y |X) = U (Ω2), Ω2 = {ε|ε ∈ [f (X) − 20, f (X) + 20]},
π2 = 0.4,
π3 = 0.3,
f (x) = 0.5x + 1, N (µ, σ2) 为均值 µ 方差 σ2 的高斯 (Gauss) 分布, Laplacian(µ, β) 表示均值为 µ 尺度
为 β 的拉普拉斯 (Laplace) 分布. 此问题最优回归曲线为 f (x). p1, p2 的作用为试图生成噪声, p3 为
生成异常值. 元数据集和测试集分别由真实回归曲线上随机生成的 1000 个点构成. 我们通过最小二
乘回归 [20] 拟合曲线, 其中损失函数以最小二乘损失 (LS) 作为对比. 通过应用 Hard, Linear, Mixture,
Meta-Hard, Meta-Linear 和 Meta-Mixture 的基本策略, 验证各自步学习算法的有效性.
表 1 给出了各个方法在测试集上的性能, 可以看出, 元自步学习算法相比于手工设计参数的原自
步学习方法, 性能得以稳步提升, 其中 Meta-Mixture 算法获得了最佳的预测效果. 图 1(a) 描绘出训练
过程中 Meta-Linear 的隐式损失函数随着迭代次数的变化曲线, 可以看出, 随着迭代次数的增加, 年龄
参数逐步增大, 更多的难样本参与训练, 说明元自步学习算法可以通过自适应学习年龄参数近似实现
了自步学习预期的由易到难的学习过程.
4.2 噪声标记分类实验
数据集. 我们选取 CIFAR-10 和 CIFAR-100 数据集用以评估各种自步学习算法在噪声标记数据
上分类的效果. 两个数据集由 32 × 32 大小的彩图组成, 分别包含 10 个类和 100 个类. 其训练集和测
试集分别由 50000 张和 10000 张图片构成. 我们从其数据集中给定的验证集随机选取 1000 张图片作
为元数据.
噪声设置. 在实验中采取两种类型的标记噪声: 对称噪声和非对称噪声. 对称噪声标记通过对给
定比例的训练样本均匀转换到其他类别的标记上形成 [31]. 非对称噪声标记通过将给定比例的样本仅
转换到特定类别的标记上构成 [24].
对比方法. 我们选取以下方法作为对比方法: (1) CE, 利用交叉熵损失在噪声数据集上训练分类
器. (2) Forward [32] 通过标签的转移矩阵矫正噪声标记. (3) GCE [33] 通过引入额外的参数使得新设计
的损失函数相比于 CE 具有噪声鲁棒性. (4) Meta-Weight-Net [24] 利用元数据通过单隐层的 MLP 学
787
束俊等: 元自步学习
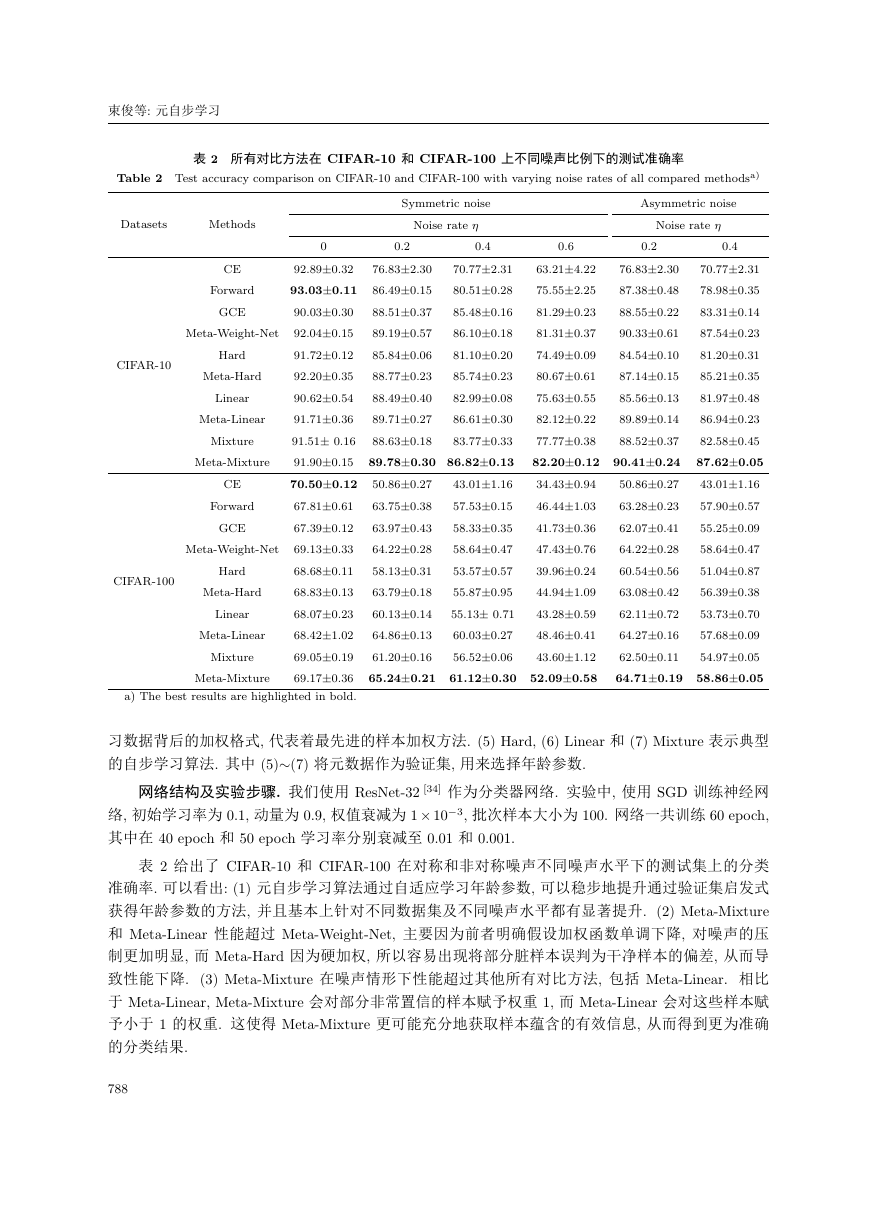
表 2 所有对比方法在 CIFAR-10 和 CIFAR-100 上不同噪声比例下的测试准确率
Table 2 Test accuracy comparison on CIFAR-10 and CIFAR-100 with varying noise rates of all compared methodsa)
Datasets
Methods
Symmetric noise
Noise rate
Asymmetric noise
Noise rate
0
0.2
0.4
0.6
0.2
0.4
70.772.31
76.832.30
63.214.22
70.772.31
76.832.30
78.980.35
87.380.48
75.552.25
80.510.28
86.490.15
83.310.14
88.550.22
81.290.23
85.480.16
88.510.37
87.540.23
90.330.61
81.310.37
86.100.18
89.190.57
81.200.31
84.540.10
74.490.09
81.100.20
85.840.06
85.210.35
87.140.15
80.670.61
85.740.23
88.770.23
81.970.48
85.560.13
75.630.55
82.990.08
88.490.40
86.940.23
89.890.14
82.120.22
86.610.30
89.710.27
82.580.45
77.770.38
88.520.37
88.630.18
83.770.33
87.620.05
82.200.12 90.410.24
89.780.30 86.820.13
43.011.16
34.430.94
50.860.27
50.860.27
43.011.16
57.900.57
63.280.23
46.441.03
57.530.15
63.750.38
55.250.09
62.070.41
41.730.36
58.330.35
63.970.43
58.640.47
47.430.76
64.220.28
64.220.28
58.640.47
51.040.87
60.540.56
39.960.24
53.570.57
58.130.31
56.390.38
63.080.42
44.941.09
55.870.95
63.790.18
53.730.70
62.110.72
43.280.59
55.13 0.71
60.130.14
57.680.09
48.460.41
64.270.16
64.860.13
60.030.27
62.500.11
61.200.16
54.970.05
43.601.12
56.520.06
64.710.19 58.860.05
65.240.21 61.120.30 52.090.58
CIFAR-10
CIFAR-100
Hard
Linear
CE
Mixture
Meta-Hard
Meta-Linear
CE
Forward
GCE
Meta-Mixture
Meta-Weight-Net
92.890.32
93.030.11
90.030.30
92.040.15
91.720.12
92.200.35
90.620.54
91.710.36
91.51 0.16
91.900.15
70.500.12
67.810.61
67.390.12
69.130.33
68.680.11
68.830.13
68.070.23
68.421.02
69.050.19
69.170.36
a) The best results are highlighted in bold.
Meta-Weight-Net
Forward
GCE
Meta-Mixture
Meta-Linear
Hard
Meta-Hard
Linear
Mixture
习数据背后的加权格式, 代表着最先进的样本加权方法. (5) Hard, (6) Linear 和 (7) Mixture 表示典型
的自步学习算法. 其中 (5)∼(7) 将元数据作为验证集, 用来选择年龄参数.
网络结构及实验步骤. 我们使用 ResNet-32 [34] 作为分类器网络. 实验中, 使用 SGD 训练神经网
3, 批次样本大小为 100. 网络一共训练 60 epoch,
络, 初始学习率为 0.1, 动量为 0.9, 权值衰减为 1× 10
其中在 40 epoch 和 50 epoch 学习率分别衰减至 0.01 和 0.001.
表 2 给出了 CIFAR-10 和 CIFAR-100 在对称和非对称噪声不同噪声水平下的测试集上的分类
准确率. 可以看出: (1) 元自步学习算法通过自适应学习年龄参数, 可以稳步地提升通过验证集启发式
获得年龄参数的方法, 并且基本上针对不同数据集及不同噪声水平都有显著提升. (2) Meta-Mixture
和 Meta-Linear 性能超过 Meta-Weight-Net, 主要因为前者明确假设加权函数单调下降, 对噪声的压
制更加明显, 而 Meta-Hard 因为硬加权, 所以容易出现将部分脏样本误判为干净样本的偏差, 从而导
致性能下降. (3) Meta-Mixture 在噪声情形下性能超过其他所有对比方法, 包括 Meta-Linear. 相比
于 Meta-Linear, Meta-Mixture 会对部分非常置信的样本赋予权重 1, 而 Meta-Linear 会对这些样本赋
予小于 1 的权重. 这使得 Meta-Mixture 更可能充分地获取样本蕴含的有效信息, 从而得到更为准确
的分类结果.
788
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
