FIR低通滤波器设计.doc-资料库

8789b07a-9ec7-4114-9349-3de17efb8ce5.doc.pdf-第1页.png

第1页 / 共11页

8789b07a-9ec7-4114-9349-3de17efb8ce5.doc.pdf-第2页.png

第2页 / 共11页

8789b07a-9ec7-4114-9349-3de17efb8ce5.doc.pdf-第3页.png

第3页 / 共11页

8789b07a-9ec7-4114-9349-3de17efb8ce5.doc.pdf-第4页.png

第4页 / 共11页

8789b07a-9ec7-4114-9349-3de17efb8ce5.doc.pdf-第5页.png

第5页 / 共11页

8789b07a-9ec7-4114-9349-3de17efb8ce5.doc.pdf-第6页.png

第6页 / 共11页

8789b07a-9ec7-4114-9349-3de17efb8ce5.doc.pdf-第7页.png

第7页 / 共11页

8789b07a-9ec7-4114-9349-3de17efb8ce5.doc.pdf-第8页.png

第8页 / 共11页

燕山大学课程设计说明书目录第一章摘要················································2 第二章滤波器简介··········································2 一、FIR 滤波器简介·············································2 二、窗函数简介·················································3 第三章滤波器参数设计······································4 第四章程序设计与仿真······································4 一、仿真用到的指令介绍·········································4 二、滤波器的程序···············································5 三、仿真结果···················································7 第五章总结················································10 第六章心得体会············································10 参考文献·····························································11 第 1 页共 11 页

燕山大学课程设计说明书第一章摘要数字滤波器是一种用来过滤时间离散信号的数字系统，通过对抽样数据进行数学处理来达到频域滤波的目的。根据其单位冲激响应函数的时域特性可分为两类：无限脉冲响应（IIR）滤波器和有限脉冲响应（FIR）滤波器。与 IIR 滤波器相比，FIR 的实现是非递归的，总是稳定的；更重要的是，FIR 滤波器在满足幅频响应要求的同时，可以获得严格的线性相位特性。因此，它在高保真的信号处理，如数字音频、图像处理、数据传输、生物医学等领域得到广泛应用。 MATLAB 是“矩阵实验室”（MATrix LABoratoy）的缩写，它是由美国 Mathworks 公司于 1984 年正式推出的，是一种面向科学和工程计算的语言，它集数值分析、矩阵运算、信号处理和图形显示于一体，具有编程效率高、调试手段丰富、扩充能力强等特点。 MATLAB 的信号处理工具箱具有强大的函数功能，它不仅可以用来设计数字滤波器，还可以使设计达到最忧化，是数字滤波器设计的强有力工具。关键字：数字滤波器、信号处理、离散信号、FIR、IIR、MATLAB 第二章滤波器简介一、FIR 滤波器简介： FIR 滤波器的基本结构可以理解为一个分节的延时线，把每一节的输出加权累加，可得到滤波器的输出。FIR 滤波器的脉冲响应 h(n)是有限长的，FIR 滤波器的设计问题实质上是确定能满足所要求的转移序列或脉冲响应的常数的问题，设计方法主要有窗函数法、频率采样法和等波纹最佳逼近法等，本次课设我使用了窗函数法。 FIR 数字滤波器的优点：首先，有限长单位脉冲响应(FIR)数字滤波器在保证幅度特性满足技术要求的同时，很容易保证严格的线性相位特性；另外，FIR 数字滤波器的单位脉冲响应是有限长的，因此，滤波器一定是稳定的，只要经过一定的延时，任何非因果的有限长序列都将变成因果的有限长序列，因而总能用因果系统来实现；最后，FIR 数字滤波器由于单位脉冲是有限长的，故可以用 FFT 算法来过滤信号，这样可以大大提高运算效率。第 2 页共 11 页

燕山大学课程设计说明书二、窗函数简介：窗函数设计法是一种通过截短和计权的方法使无限长非因果序列成为有限长脉冲响应序列的设计方法。通常在设计滤波器之前，应该先根据具体的工程应用确定滤波器的技术指标。在大多数实际应用中，数字滤波器常常被用来实现选频操作，所以指标的形式一般为在频域中以分贝值给出的相对幅度响应和相位响应。常用的窗函数有如下几种：（1）、矩形窗(Rectangle Window)：窗函数为： ( ) w n R  ( ) R n N 其频率响应为： ( W e R jw )  sin sin wN w / 2 / 2  1 Nj  2 w e RW e 的主瓣宽度为 4/N，第一旁瓣比主瓣低 13dB,最小阻带衰减为 21dB。 )jw ( （2）、汉宁(Hanning)窗，又称升余弦窗：窗函数为： w n Hn ( ) 0.5[1 cos(   2 n  )] ( ) w n R 1 N  当 N>>1 时，N—1  N，此时，汉宁窗的幅度函数为： 2  )] N ) 0.25[  2  ) N W w ) 0.5  W w W w W w    Hn ( ( ( ( R R R 可见， ( HnW w 是由三部分相加得出的，能量更集中在主瓣中。主瓣宽度为 8/N， ) 第一旁瓣比主瓣低 31dB,阻带最小衰减为 44dB。（3）、哈明(Hamming)窗，又称改进的升余弦窗：窗函数为： w Hm )( n  54.0[  当 N>>1 时，其幅度响应为： 2(46.0 n  )( )] nw 1 N  R ) wW ( Hm  54.0 wW ( [23.0)  wW ( R R  )2  N  wW ( R  )2  N 这种改进的升余弦窗，可将 99.96%的能量集中在窗谱的主瓣内，与汉宁窗相比，主瓣宽度相同，但第一旁瓣比主瓣低 41dB，最小主瓣衰减为 53dB。第 3 页共 11 页

燕山大学课程设计说明书（4）、布莱克曼窗（Blackman）：窗函数为： ( ) w n Bl  [0.42 0.5cos  幅度函数为： 2 n  1 N   0.08cos 4 n  ] 1 N  ( ) R n N ) wW ( Bl  42.0 wW ( [25.0)  wW ( R  R  [04.0 wW ( R  4  1 N  )  wW ( R  wW ( R  2  )] 1 N   2  ) 1 N  4  )] 1 N  其幅度函数由五部分组成，他们都是移位不同，且幅度也不同的函数，使旁瓣进一步抵消。阻带衰减进一步增加主瓣宽度是矩形窗的 3 倍，即 12 /N。（5）凯塞-贝塞尔(Kaiser-Basel)窗：窗函数为： ( ) w n k  I I 0 0 ( )  ) (  ， 0   n N  1 式中，   1 (  2 n N  1 2  1) ，是一个可选参数，用来选择主瓣宽度和旁瓣衰减之间的交换关系，一般说来，β越大，过渡带越宽，阻带越小衰减也越大。第三章滤波器参数设计根据任务书中要求，正弦信号的频率为 1/16Hz，白噪声长度为 500，所设计的低通滤波器的长度为 11。经过多次尝试，得出当采样周期 sf =21 时，正好有一个半周期的正弦信号显示在窗口中，视觉效果较好。当 sf =21 时，计算并取近似得截止频率可取为 0.007，经程序仿真验证得出截止频率为 0.007 时，滤波效果很好。第四章程序设计与仿真一、仿真用到的指令介绍： Plot 线性图形 Figure 建立图形，系统自动从 1，2，3，4...来建立图形，数字代表第几幅图形 Randn 正态分布的随机数矩阵 Abs 绝对值第 4 页共 11 页

燕山大学课程设计说明书 Pi 圆周率 b0=boxcar( n1 )、b1 = hamming (n1)，b2=hanning (n1)，b3 = blackman (n1) ， b4=kaiser(n1,beta)分别表示调用矩形窗、哈明窗、汉宁窗、布莱克曼窗和凯瑟窗 fir1 窗函数法设计 FIR 滤波器 freqz 计算数字滤波器的频率响应 hold on 添加图形，画不同的图形在一个窗口里时要用 legend 图形图例 fftfilt 实现卷积运算二、滤波器的程序：所设计的滤波器的程序如下： N=500; n=0:N-1; f=1/16; fs=21; x0=sin(2*pi*f*n/fs); NOISE=randn(1,500); x=x0+NOISE; figure(1); plot(n,x0,'co'); figure(2); plot(n,x); n1=11; beta=10; b0=boxcar(n1); b1=hamming(n1); b2=hanning(n1); b3=blackman(n1); 第 5 页共 11 页

燕山大学课程设计说明书 b4=kaiser(n1,beta); h0=fir1(n1-1,0.007,b0); h1=fir1(n1-1,0.007,b1); h2=fir1(n1-1,0.007,b2); h3=fir1(n1-1,0.007,b3); h4=fir1(n1-1,0.007,b4); [h0,f0]=freqz(b0,1,512,2); [h1,f1]=freqz(b1,1,512,2); [h2,f2]=freqz(b2,1,512,2); [h3,f3]=freqz(b3,1,512,2); [h4,f4]=freqz(b4,1,512,2); figure(3); plot(f0,20*log10(abs(h0)),'r'); hold on plot(f1,20*log10(abs(h1)),'y'); hold on plot(f2,20*log10(abs(h2)),'black'); hold on plot(f3,20*log10(abs(h3)),'g'); hold on plot(f4,20*log10(abs(h4))); legend('矩形窗','海明窗','汉宁窗','布莱克曼窗','凯瑟窗'); y0=fftfilt(h0,x) y1=fftfilt(h1,x); y2=fftfilt(h2,x); y3=fftfilt(h3,x); 第 6 页共 11 页

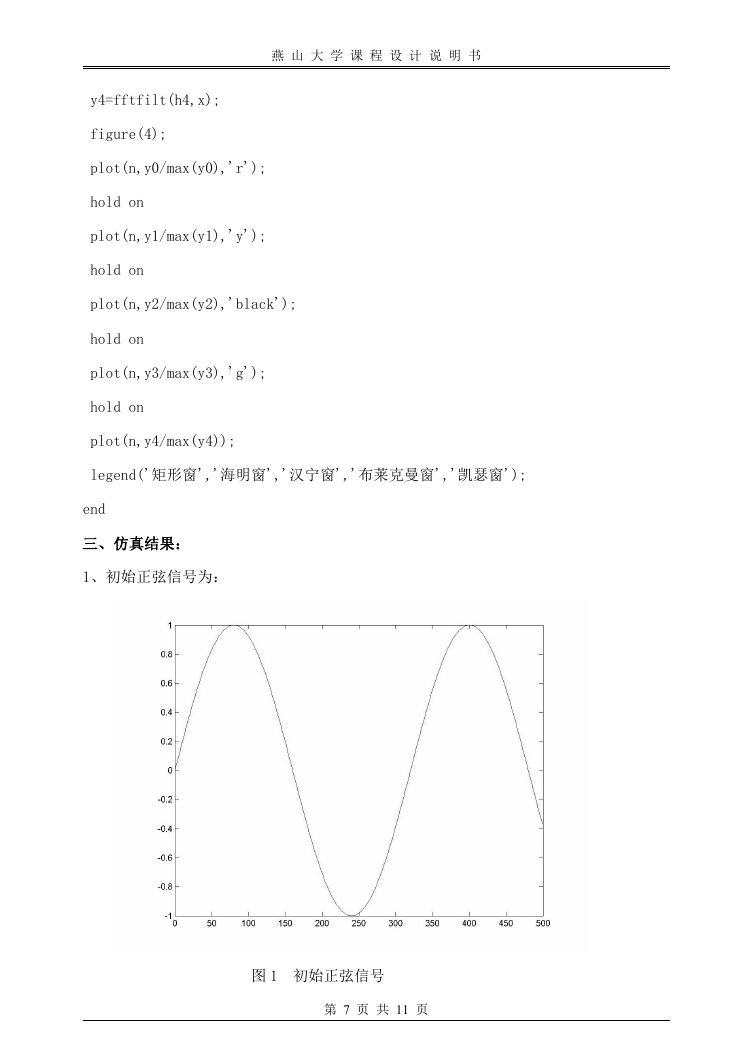
燕山大学课程设计说明书 y4=fftfilt(h4,x); figure(4); plot(n,y0/max(y0),'r'); hold on plot(n,y1/max(y1),'y'); hold on plot(n,y2/max(y2),'black'); hold on plot(n,y3/max(y3),'g'); hold on plot(n,y4/max(y4)); legend('矩形窗','海明窗','汉宁窗','布莱克曼窗','凯瑟窗'); end 三、仿真结果： 1、初始正弦信号为：图 1 初始正弦信号第 7 页共 11 页

燕山大学课程设计说明书 2、噪声信号为：图 2 噪声信号 3、所用到的五种窗函数的幅度谱：图 3 窗函数的幅度谱第 8 页共 11 页

资料库

FIR低通滤波器设计.doc

相关推荐

后端

热门标签

最新资料