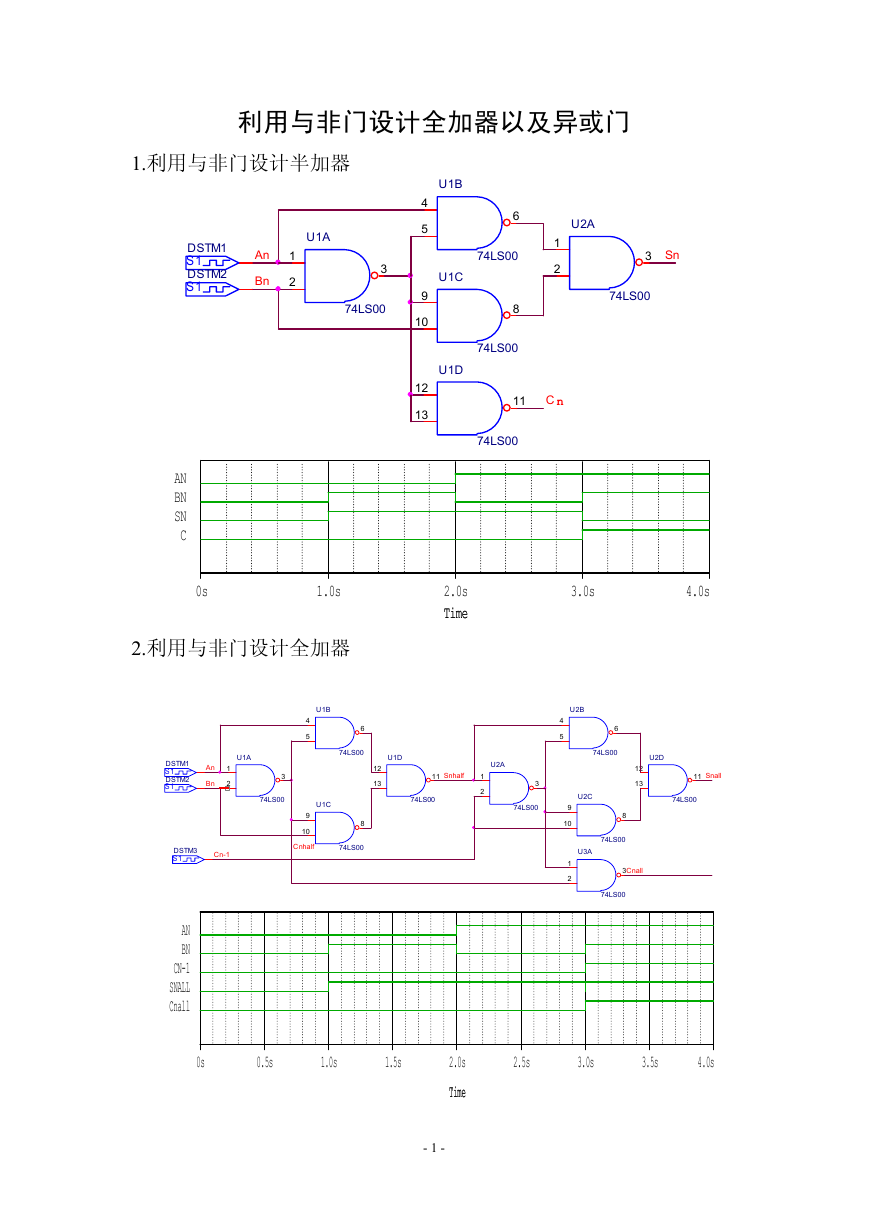
利用与非门设计全加器以及异或门 1.利用与非门设计半加器 U1A DSTM1 S1 DSTM2 S1 An Bn 1 2 3 74LS00 U1B U1C U1D 4 5 9 10 12 13 6 U2A 1 2 3 Sn 74LS00 74LS00 8 74LS00 11 n C 74LS00 AN BN SN C 0s 1.0s 2.0s Time Time 3.0s 4.0s 2.利用与非门设计全加器 U1A DSTM1 S1 DSTM2 S1 An Bn 1 2 3 74LS00 U1B 6 74LS00 U1D 12 13 8 U1C 4 5 9 10 11 Snhalf 74LS00 U2A 1 2 3 74LS00 DSTM3 S1 Cn-1 Cnhalf 74LS00 U2B 4 5 6 74LS00 U2D 12 13 11 Snall 74LS00 U2C U3A 9 10 1 2 8 74LS00 Cnall 3 74LS00 AN BN CN-1 SNALL Cnall 0s 0.5s 1.0s 1.5s 2.5s 3.0s 3.5s 4.0s 2.0s Time Time - 1 - 

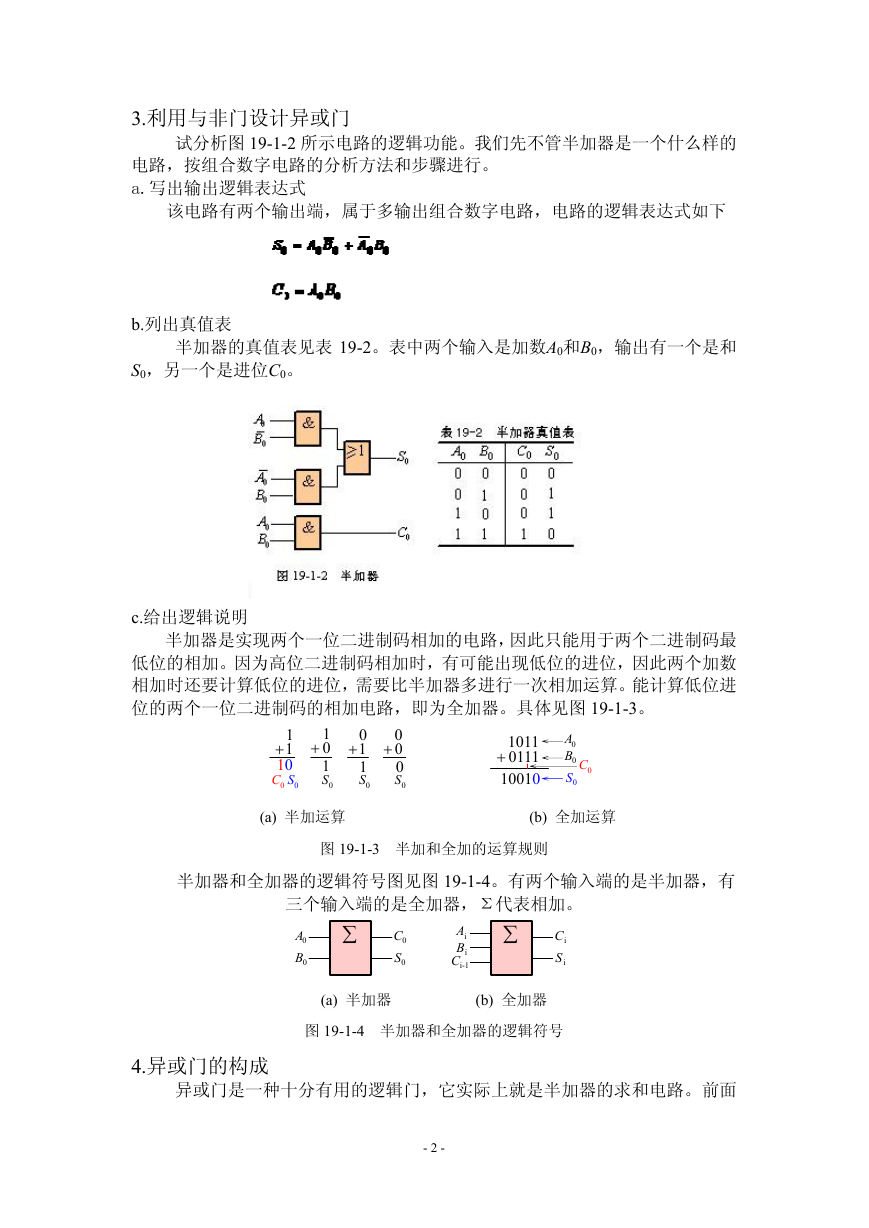
3.利用与非门设计异或门 试分析图 19-1-2 所示电路的逻辑功能。我们先不管半加器是一个什么样的 电路，按组合数字电路的分析方法和步骤进行。 a.写出输出逻辑表达式 该电路有两个输出端，属于多输出组合数字电路，电路的逻辑表达式如下 b.列出真值表 半加器的真值表见表 19-2。表中两个输入是加数A0和BB0，输出有一个是和 S0，另一个是进位C0。 c.给出逻辑说明 半加器是实现两个一位二进制码相加的电路，因此只能用于两个二进制码最 低位的相加。因为高位二进制码相加时，有可能出现低位的进位，因此两个加数 相加时还要计算低位的进位，需要比半加器多进行一次相加运算。能计算低位进 位的两个一位二进制码的相加电路，即为全加器。具体见图 19-1-3。 1 1+ 0 1 0C 0S 1 0+ 1 0S 0 1+ 1 0S 0 0+ 0 0S 1011 0111 + 10010 0A 0B 0S 0C (a) 半加运算 (b) 全加运算 图 19-1-3 半加和全加的运算规则 半加器和全加器的逻辑符号图见图 19-1-4。有两个输入端的是半加器，有 三个输入端的是全加器，Σ代表相加。 ∑ 0A 0B 0C 0S ∑ iA iB i-1C iC iS (a) 半加器 (b) 全加器 图 19-1-4 半加器和全加器的逻辑符号 4.异或门的构成 异或门是一种十分有用的逻辑门，它实际上就是半加器的求和电路。前面 - 2 - 

已经提到异或逻辑关系式为 + 对于图 19-1-5(a)，输出逻辑表达式是 = BABABAY ⊕= 实际上它可以变换为 ABAY = ⋅ ABB ABB ABAY ⋅ = ABA ABB + = BAA ( ) + = + BABA + = BA ⊕= BAB ( + ) A B & & & & Y A B 1= Y (a) 异或门逻辑图 (b) 异或门符号 图 19-1-5 异或门逻辑图及符号 异或门的逻辑符号见图 19-1-5(b)，异或门的真值表十分简单，当 A=B 时， 即 A=B=0 时，或 A=B=1 时，Y=0；当 A≠B 时，即 A=0、B=1 时，或 A=1、B=0 时，Y=1。异或门逻辑符号中的=1，表明输入变量中有一个“1”时，输出为“1”。 而或门中的特征符号是≥1，表示输入变量中有一个“1”或一个以上“1”时， 输出即为“1”。 请注意，每一个异或门只有二个输入变量，而异或运算可以对多个输入变 量进行，多个变量异或运算的规律读者可以自行总结。 - 3 -