关于地震波分析的MATLAB课设(含源代码).docx

发布时间：2022-06-09 发布人：admin 分类：说明书资料大小：0.36M 资料格式：docx 举报版权申诉

weixin_44472384-12060263-16359647316934163710.docx.pdf-第1页.png

第1页 / 共7页

weixin_44472384-12060263-16359647316934163710.docx.pdf-第2页.png

第2页 / 共7页

weixin_44472384-12060263-16359647316934163710.docx.pdf-第3页.png

第3页 / 共7页

weixin_44472384-12060263-16359647316934163710.docx.pdf-第4页.png

第4页 / 共7页

weixin_44472384-12060263-16359647316934163710.docx.pdf-第5页.png

第5页 / 共7页

weixin_44472384-12060263-16359647316934163710.docx.pdf-第6页.png

第6页 / 共7页

weixin_44472384-12060263-16359647316934163710.docx.pdf-第7页.png

第7页 / 共7页

（一）目标和思路

1.题目

2.目标

3.思路

（二）源代码及运行截图

（三）结论

（四）参考文献

数字信号处理答辩报告学专院业年级班别学号学生姓名 2019 年 12 月

（一）目标和思路 1.题目采用喀什地震台日常检测中记录到的一个地震信号的记录图，发震时刻 2003 年 07 月 24 日 10 时 10 分，震中距喀什地震台 121km。 2.目标更清楚地了解信号中的频率成分，去除原始地震信号中夹杂着多种干扰。 3.思路 ①利用快速 Fourier 变换（FFT）对原始地震信号（数字信号）进行频谱分析。 ②根据快速 Fourier 变换（FFT）的结果，分析出干扰信号、有效信号以及确定所需要的滤波器参数。 ③再根据地震波干扰的频谱范围和特点，选择相应的滤波器和窗函数。 ④设计滤波器并绘出滤波器幅频相频特性。 ⑤对信号进行滤波。 ⑥绘出原始波形序列和滤波后的波形序列并进行比较。（二）源代码及运行截图源代码： load grbx3.txt; Xt=grbx3; Fs=50; dt=1/Fs; N=length(Xt); Xf=fft(Xt); %读取数据序列 %把数据赋值给变量 %设定采样率单位(Hz) %求采样间隔单位(s) %得到序列的长度 %对信号进行快速 Fourier 变换(FFT) subplot(2,1,1),plot([0:N-1]/Fs,Xt); xlabel('时间/s'),title('时间域'); ylabel('振幅'); grid on; %绘制原始值序列

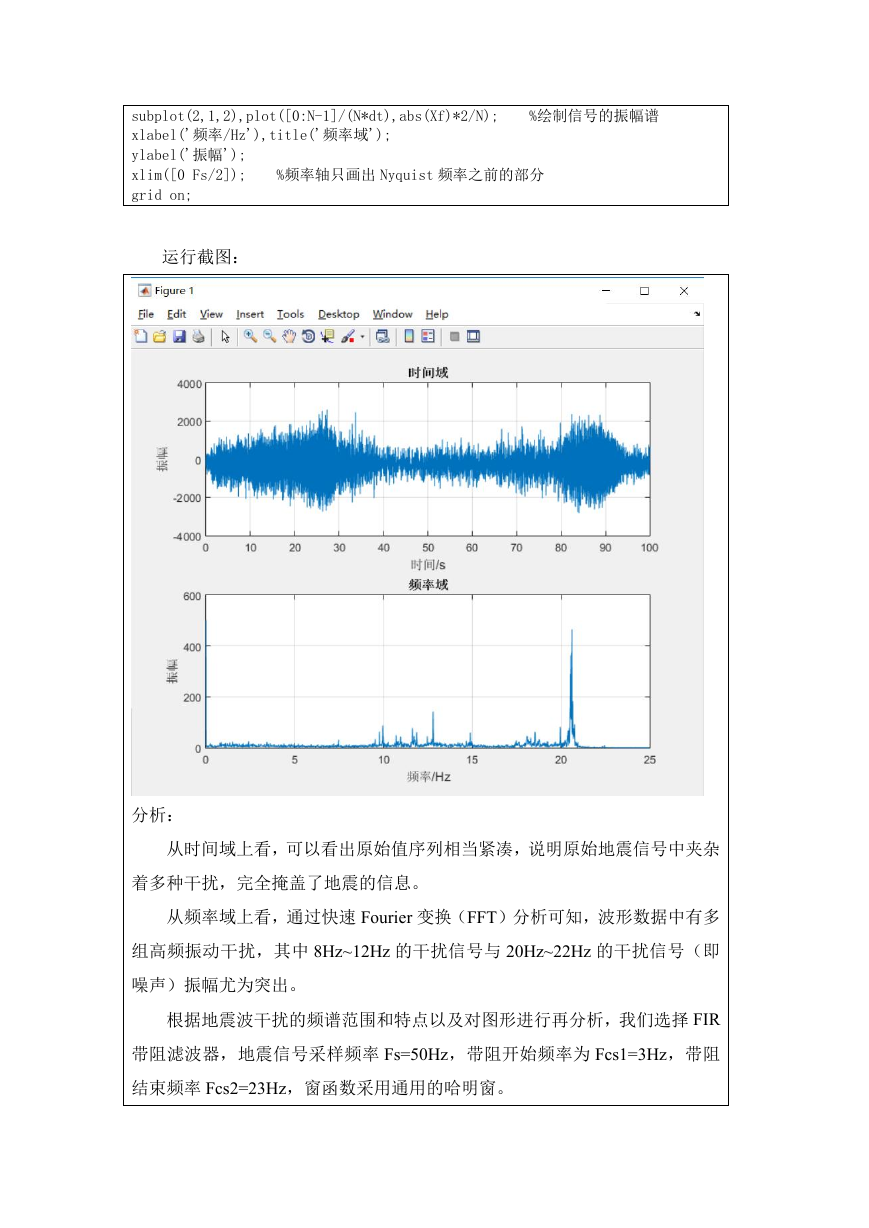
subplot(2,1,2),plot([0:N-1]/(N*dt),abs(Xf)*2/N); xlabel('频率/Hz'),title('频率域'); ylabel('振幅'); xlim([0 Fs/2]); grid on; %频率轴只画出 Nyquist 频率之前的部分 %绘制信号的振幅谱运行截图：分析：从时间域上看，可以看出原始值序列相当紧凑，说明原始地震信号中夹杂着多种干扰，完全掩盖了地震的信息。从频率域上看，通过快速 Fourier 变换（FFT）分析可知，波形数据中有多组高频振动干扰，其中 8Hz~12Hz 的干扰信号与 20Hz~22Hz 的干扰信号（即噪声）振幅尤为突出。根据地震波干扰的频谱范围和特点以及对图形进行再分析，我们选择 FIR 带阻滤波器，地震信号采样频率 Fs=50Hz，带阻开始频率为 Fcs1=3Hz，带阻结束频率 Fcs2=23Hz，窗函数采用通用的哈明窗。

源代码： load grbx3.txt; Xt = grbx3; Fs=50; dt=1/Fs; n=1:length(Xt); Nn=length(Xt); t=n/Fs; %读取数据序列 %把数据赋值给变量 %设定采样率 %计算采样间隔 %序列长度 %时间序列 Fcs1=3;Fcs2=23; Ws1=Fcs1/(Fs/2); Ws2=Fcs2/(Fs/2); Wn=[Ws1 Ws2]; wdelta=Ws2-Ws1; N=ceil(8*pi/wdelta); %N=400; pa=(N-1)/2/Fs; b=fir1(N,Wn,'stop'); %设置的通带和阻带边界频率 %转换为归一化频率 %阻带归一化频率 %过度带宽 %求得滤波器的阶数 %计算相位延迟 %设计 FIR 带阻滤波器 %绘制滤波器幅频相频特性 figure(1); [H,f]=freqz(b,1,Nn,Fs); subplot(2,1,1),plot(f,20 * log10(abs(H))); xlabel('频率/Hz');ylabel('振幅/dB');grid on; subplot(2,1,2),plot(f,180/pi * unwrap(angle(H))); xlabel('频率/Hz');ylabel('相位/^o');grid on; %求出滤波器幅频相频特性 figure(2) subplot(2,1,1),plot(t,Xt); xlabel('时间/s');ylabel('振幅');title('滤波前的信号') grid on; %绘制原始波形序列 Yt=filter(b,1,Xt); t=t-pa; subplot(2,1,2),plot(t,Yt); ylim([-600 200]); xlabel('时间/s');ylabel('振幅');title('滤波后信号'); xlim([0 max(t)+1]);grid on; %对信号进行滤波 %计算相位延迟 %绘制滤波后波形序列 %对过滤前的信号进行快速 Fourier 变换（FFT） %对过滤后的信号进行快速 Fourier 变换（FFT） %过滤前后信号的频率域对比 Xf=fft(Xt); Yf=fft(Yt); figure(3) subplot(2,1,1),plot([0:Nn-1]/(Nn*dt),abs(Xf)*2/Nn);%绘制过滤前的信号的频率域 xlim([0 Fs/2]);grid on; xlabel('频率/Hz');ylabel('振幅');grid on;title('滤波前信号的频率域') subplot(2,1,2),plot([0:Nn-1]/(Nn*dt),abs(Yf)*2/Nn);%绘制过滤后的信号的频率域 xlim([0 Fs/2]);grid on; xlabel('频率/Hz');ylabel('振幅');grid on;title('滤波后信号的频率域')

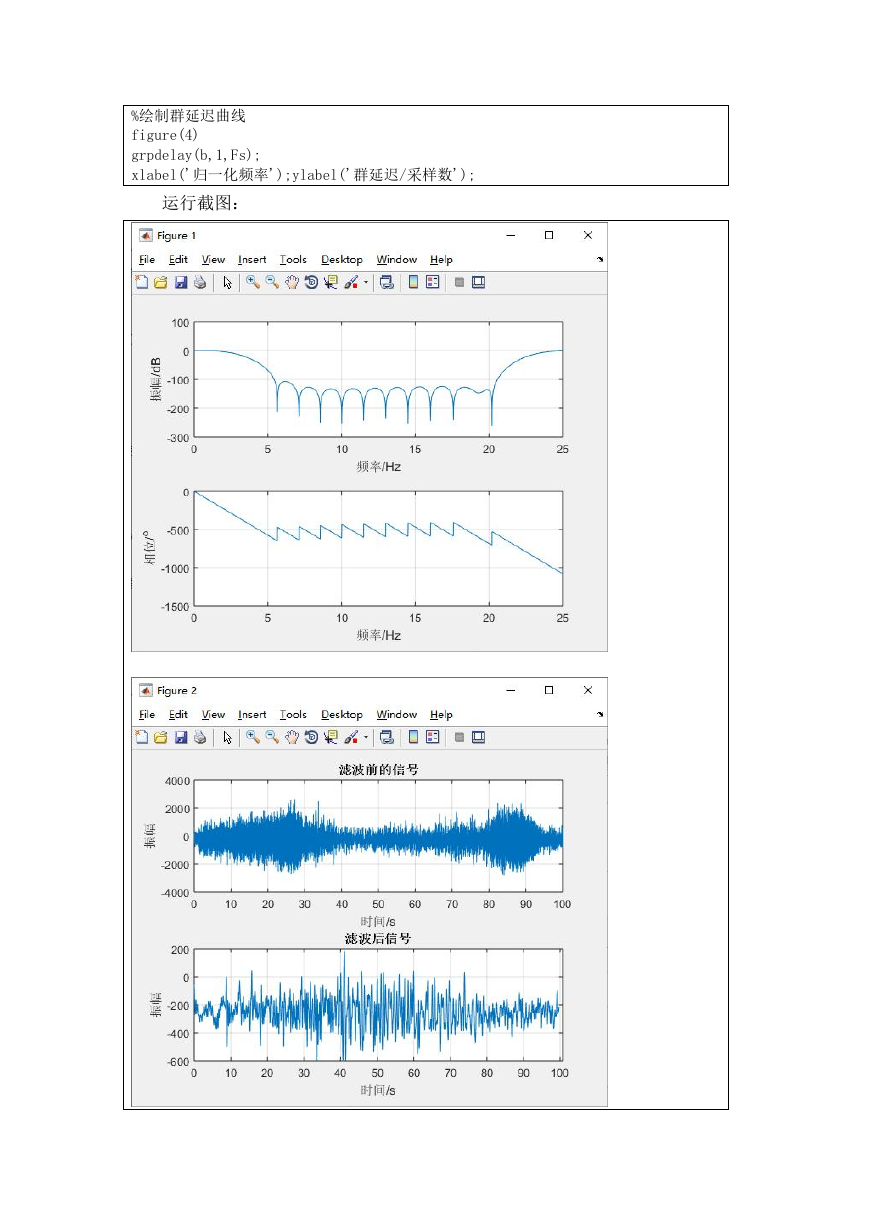
%绘制群延迟曲线 figure(4) grpdelay(b,1,Fs); xlabel('归一化频率');ylabel('群延迟/采样数'); 运行截图：

分析：通过 figure1 和 figure2，可以看出：信号通过滤波器后滤除了高频振动干扰，滤波之前地震波形完全被高频干扰所掩盖，通过滤波后可以很容易分辨出

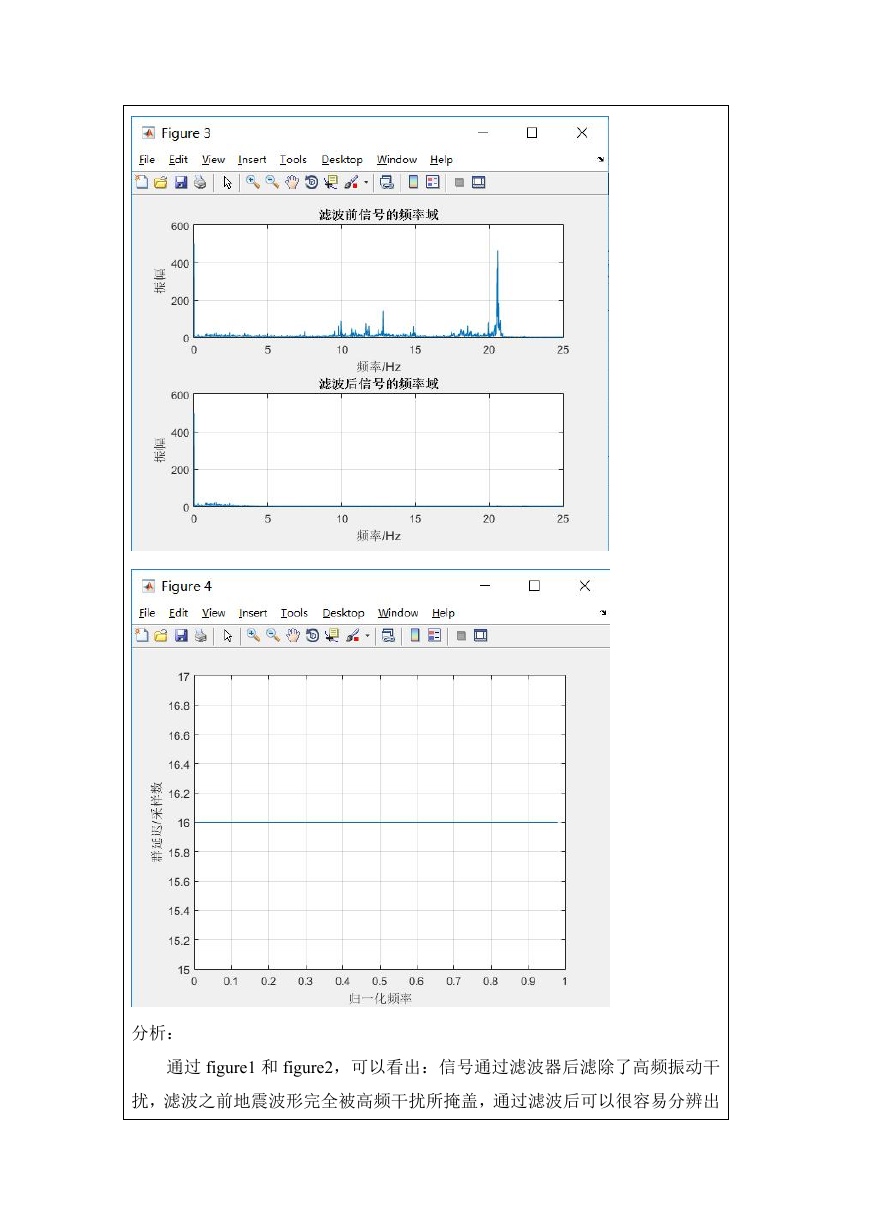
地震波的各种震相。并且滤波后信号的相位无失真，滤波器达到了预期的要求。 figure3 是过滤前后信号的频率域对比，结合 figure2，两者就是信号在滤波前后的振幅谱了。信号通过滤波后的频谱特性可以看出，滤波器对 3Hz~23Hz 的成分进行了滤除，可见滤波器达到了有效抑制干扰信号的目的。 figure4 是绘制的群延迟曲线。（三）结论运用 MATLAB 软件语言可以很容易对信号进行频谱分析和设计出满足要求的滤波器。在对数字信号进行频谱特征的分析后可以分辨出地震信息与干扰信息的频率分布特征，从而为滤波器的设计滤波参数提供依据。在设计滤波器时要根据要求选取通带临界频率和阻带临界频率，选取适当的滤波器。对于两个相近频率的信号去除要根据需要选择很好的滤波方法。从而有效的滤除对于研究而言无用的频率成分和最大限度保留有用的频率成分。另外，可根据地震或前兆信号特征选择信号处理方法设计符合要求的滤波器，滤波器还可以对信号进行积分、仿真工作。为地震观测和前兆信息处理服务。数字地震记录的信息丰富，可以更深入的对数字地震资料的各种干扰进行分析。找出干扰频率的频谱特点，做出各种干扰的频谱分析图谱。对了解台站的基本干扰背景有很大帮助。（四）参考文献 [1] 万永革.数字信号处理的 MATLAB 实现(第二版)[M].北京: 科学出版社,2012. [2] 陈鲁刚,王锐锋.用 MATLAB 实现滤波器对数字地震资料处理初探[J].防灾技术高等专科学校学报,2006,(8):62-65.

分享到：

赞收藏

资料库

关于地震波分析的MATLAB课设(含源代码).docx

相关推荐

课程资源

热门标签

最新资料