沪深300指数日收益率时间序列特征分析.pdf

发布时间：2022-05-30 发布人：admin 分类：说明书资料大小：0.29M 资料格式：pdf 举报版权申诉

weixin_38742571-12106761-16359647465091995793.pdf-第1页.png

第1页 / 共11页

weixin_38742571-12106761-16359647465091995793.pdf-第2页.png

第2页 / 共11页

weixin_38742571-12106761-16359647465091995793.pdf-第3页.png

第3页 / 共11页

weixin_38742571-12106761-16359647465091995793.pdf-第4页.png

第4页 / 共11页

weixin_38742571-12106761-16359647465091995793.pdf-第5页.png

第5页 / 共11页

weixin_38742571-12106761-16359647465091995793.pdf-第6页.png

第6页 / 共11页

weixin_38742571-12106761-16359647465091995793.pdf-第7页.png

第7页 / 共11页

weixin_38742571-12106761-16359647465091995793.pdf-第8页.png

第8页 / 共11页

1. 引言

2. 模型和数据描述

3. 沪深300指数收益的时间序列特征

4. 用EGARCH(1,1)-M模型对沪深300指数日收益进行分析

5. 结论

参考文献

中国科技论文在线 http://www.paper.edu.cn 沪深 300 指数日收益率时间序列特征分析 ——兼论印花税变动对其影响林帅东南大学经济管理学院，南京(211189) E-mail: lsfudan@sina.com 摘要：沪深 300 指数作为我国代表性最好的指数，由于诸多优势最终被选中作为股指期货的标的指数，所以对其进行深入的研究有着很重要的意义。本文在检验沪深 300 指数日收益率的相关时间序列特征的基础上，用 EGARCH-M 模型对其进行了分析。分析中同时检验了印花税上调对沪深 300 指数日收益率和日收益率波动的影响。研究结果表明沪深 300 指数日收益率服从非正态分布但是是平稳的，收益率波动存在丛集性，但杠杆效应不明显；收益主要来自于风险溢价；印花税上调对收益率和收益率的波动影响比较小。关键词：沪深 300 指数；印花税；波动性；风险溢价；EGARCH-M 模型中图分类号：F832.42 1. 引言所谓股票价格指数是指由证券交易所或金融服务机构通过抽取市场中一定数量的具有代表性和影响力的股票，运用某种特定的计算方法编制，然后公开发布的能够反映市场总体行情的指标，投资者据此可以检验自己投资的效果，并用以预测股票市场的动向。股票指数不仅是经济发展的风向标，很大程度上也代表了社会政治和文化的发展水平。正因为指数如此重要，国内学者对其做过很多研究。例如，金洪飞（2003）利用不对称的 ARCH(3)-M 模型对上海股市的波动性、风险溢价、收益率和波动的周末效应做了比较全面的研究，表明上海股市收益率有着尖峰厚尾(Leptokurtic and Fat-TAiled)的特征、股市波动存在丛集效应（Volatility Clustering）和杠杆效应(Leverage Effects)，且存在明显的周末效应 (Weekend Effects)。范钛和张明善（2002）以有效市场假说（EMH）和标准的随机游走模型 (Random Walk Model)为基础，利用沪深股市近十年的历史数据对沪深市场的周末收益率效应和波动性效应进行了全面的检验，表明中国证券市场也存在与西方市场类似的周末效应, 周末收益率大大低于周内收益率(甚至为负)，但沪深两市周末效应显著性不同,上海证券市场的周末效应更加明显。彭俊衡(2003)从套期保值效果、市场覆盖率、市场认可度等方面对中国当时的几种股票指数进行了分析和比较,认为当时的股票指数都不能满足股指期货的要求, 提出了应推出两市联合指数作为股指期货标的指数。正是由于市场要求有更具代表性的、编制更为规范的指数出现，我国于 2005 年 4 月 8 日由沪深证券交易所第一次联合正式发布用于反映 A 股市场整体走势的指数——沪深 300 指数，以 2004 年 12 月 31 日为基日,基点为 1000 点。它从上海和深圳证券市场中选取 300 只 A 股作为样本成份股，覆盖了沪深市场六成左右的市值，具有良好的市场代表性，因此能够反映中国证券市场股票价格变动的概貌和运行状况,并能够作为投资者特别是机构投资者的业绩评价标准，它的发布也为指数化投资及指数衍生产品创新提供了基础条件。根据邢精平、骆君生（2006）和赵亮（2006）等的研究，由于沪深 300 指数具有明显的相对优势（编制规则合理、覆盖面广、流动性好、套保效果好、抗操纵性强等），所以是作为我国首 - 1 -

中国科技论文在线 http://www.paper.edu.cn 只股指期货标的指数的最佳候选者。事实上，中国金融期货交易所（CFFEX）于 2006 年 10 月 30 日开始的股指期货仿真交易，合约的标的就是沪深 300 指数，所以在目前国内股指期货即将推出之际，对沪深 300 指数做进一步的研究就显得十分重要和有意义。另外，出于对资本市场泡沫的担忧，财政部从 2007 年 5 月 30 日起将证券（股票）交易印花税税率由１‰上调为３‰，其目的是通过提高交易成本来稳定投资者的心理预期，抑制过度投机，从而进一步促进证券市场的健康稳定发展。受印花税上调影响，沪深两市当日暴跌，上证指数及深证成指收盘跌幅分别高达 6.50%、6.16%，沪深 300 指数也重挫 6.76%，并在随后几日连续大幅度下行，最低达到 3246.73 点，总体下降幅度高达约 22%之多，可见其对我国股市的影响是巨大的。从国外学者的研究文献来看,交易费用对证券市场的具体影响颇具争议：有很多学者认为证券市场印花税调整与市场波动性成反比，例如 Tobin (1974, 1978)Stiglitz (1989)认为交易税可以抑制证券市场的过度波动；Jackson 和 O′Donnell (1985) 用英国的季度数据研究表明，印花税从 2%降低到 1% ，市场波动性将提高 70%，Lindgren 和 Westlund(1990) 以及 Ericsson 和 Lindgren (1992)分别用瑞典和跨国数据的实证分析发现，长期来看，印花税上升 1 个百分点将导致市场波动性分别下降 50 %和 70 %。但另一些学者的研究却表明印花税对股市波动性几乎没有影响，例如 Saporta 和 Kan (1997)采用了新的经济计量方法，发现英国的印花税已被资本化在价格之中，因此其调整对证券价格和市场的波动性都没有影响。东北财经大学金融工程研究中心与华夏证券研究所联合课题组(2002)对中国证券市场交易费用的市场效应作了经验研究，结果表明证券交易印花税税率调整对证券市场的股票价格具有敏感冲击反应，并且提高印花税会导致市场收益波动性的加大，而且在 10 个交易日内市场反应最大，随着时间的推移，反应逐渐减少。范南、王礼平（2003）通过对我国证券市场历次印花税调整的研究发现印花税上调会导致市场收益波动性的提高，印花税下调会导致市场收益波动性的降低，并因此建议政府应进一步下调印花税税率来降低市场波动性和噪声波动性,促进市场效率。所以本文中将对这次印花税调整对沪深 300 指数的日收益率和日收益率波动进行实证检验，来分析其具体影响如何。本文的结构安排如下：第二部分简要介绍 ARCH 族模型特别是本文中将采用的 EGARCH-M 模型，以及简要描述沪深 300 指数相关数据的来源和处理；第三部分对沪深 300 指数日收益率的时间序列特征（包括正态性、平稳性、序列相关性、异方差、杠杆效应）做了简要的检验和分析；第四部分主要是用 EGARCH(1,1)-M 模型对沪深 300 指数日收益率进行建模并分析；第五部分我们对本文进行总结得出结论。 2. 模型和数据描述由于金融资产收益序列大多存在波动的丛集性，在金融经验分析中，自回归条件异方差模型(ARCH) 被专门用于波动性的建模和预测。ARCH 模型通常包括均值方程（Mean Equation）和方差方程(Variance Equation)，在方差方程中，应变量的方差被表示为前几次误差项的平方以及应变量或外生变量的函数。最早的 ARCH 模型由 Engle（1982）提出， Bollerslev（1986）把它扩展为 GARCH 模型，即广义自回归条件异方差模型。Engle、Lilien 和 Robins（1987）则把条件方差(Conditional Variance)引入均值方程中，提出了条件异方差均值模型（ARCH-M）。为了克服 GARCH 模型在处理金融事件序列数据时的一些不足， Nelson（1991）提出了指数 GARCH 模型（EGARCH），该模型考虑了正负资产收益之间的不对称性。此外还有 TARCH、PGARCH、VAR-GARCH 等等。下面我们对本文中要用到的相关模型进行简要的介绍： - 2 -

中国科技论文在线 http://www.paper.edu.cn ARCH(q)模型的一般形式为： r t u t     2 u    t v   t t 2   t   u 2 t 1 1  u 2 t  ...  0 2  q u2 t q  （1）其中第一个为均值方程，第三个方程为方差方程，第二个方程中 tv N (0,1) t ，它与在 t 时刻是不相关的，说明服从于条件异方差分布。在方差方程中，为了保证无条件方差存在并有限，还要满足非负约束，即 tu 0  i 0  ， 0 ARCH(q)-M 模型的一般形式是将上述(1)式中均值方程改为： 0)  ，且 i 1(  1  i 0    2  1 ...    q  q   i 1 。 r t     t tu  （2） 2 引入均值方程是因为考虑到收益往往是和风险相关的，风险是影响收益的主将或要因素之一，风险越大，收益越高，所以一般来说 0 。不对称的 ARCH(q)模型 TARCH 的一般形式是将上述(1)式中方差方程改为：     2  1t u d 2 t 1    u 2 q t q  u 2 t 1 1  u 2 t   ...     0  （3） 2 t 其中为虚拟变量，当（利好消息）时，取值为 1，否则取值为 0。所以当有利 1tu  的系数为 1 。因为利好消息引起波动 1  ，当有利空消息时 2 好消息时的系数为的幅度往往比利空消息引起的波动幅度小，所以我们预期 0 。由于 ARCH 模型残差平方的滞后阶数 q 很难确定，而且如果把所有的依赖关系都考虑进来的话，q 值将非常大，此时模型将会变得过于庞大，自由度相应就比较小。并且还存在这样一个问题，即在其它条件相同的情况下，如果条件方差方程中参数越多，就越有可能违反非负约束，使得模型估计没有意义。为了克服上述问题，Bollerslev（1986）和 Tylor（1986）各自独立发展起来广义的 ARCH 模型（GARCH）。一般来讲，用 GARCH（1，1）就能充分捕获数据中的波动丛集性，因此高阶 GARCH 很少被使用，所以我们也采用 GARCH(1,1) 模型，它是将上述(1)式中的方差方程的形式改为： tu 2 2     1t 1 1     2 t 0 （4） GARCH 模型允许条件方程依赖于自身的前期值，实际上是条件方差的 ARMA 模型。它可以展开为无穷阶的 ARCH 模型，但 GARCH 模型看上去，形式更为简单，待估参数数目较少，避免了过度拟合。 GARCH-M 模型是采用类似如上 ARCH-M 模型的方法将 t 引入到均值方程，而不对称的 GARCH 模型 EGARCH 是由 Nelson（1991）提出，它的方差方程的一般形式为： log( 2     t  log(   2 t ) )   1 u t 1  2  t  1       u t 1  2  t  1  2      （5） - 3 - 2 tu  0 td tu  2 1

中国科技论文在线 http://www.paper.edu.cn 这个模型有如下几个优点：首先，由于我们是对对模型的参数施加非负约束；其次，我们预期 0 ，因为这样的话，当有利空消息（ log( 2  t ) 进行建模，因此不需要人为地 0 ） tu  ，此时坏消息引起的波动比好消息引起的 tu  0 0 tu  ，当有利好消息( 时，波动更大，所以我们可以用它来衡量杠杆效应。 tu  )时, 0 本文中所用的沪深 300 指数的日收盘价数据来自于 Wind 资讯，样本期为 2002 年 1 月 7 日至 2007 年 12 月 14 日(注：该指数在 2005 年 4 月 8 日发布，此前的数据是根据基点按照编制规则往后推算出来的)，共 1435 个数据。 rhs 300 rhs 表示日收益率，它为对沪深 300 指数取对数差分后得到，即 300 t _ 300 ) 1  _ 300 / t clpr hs clpr hs _ 300 ) t clpr hs ln( ln( ln(    t clpr hs _ 300 ) 1  t clpr hs _ 300 代表沪深 300 指数日收盘价，（ 6） 3. 沪深 300 指数收益的时间序列特征图 1 和图 2 分别是沪深 300 指数收盘价走势图和其日收益率的波动图形。我们先从以下几个方面对沪深 300 指数日收益的一些相关特征进行分析。 3.1 正态性（Normality）金融时间序列通常是非正态分布的，沪深 300 指数日收益数据也是如此。从图 3 的描述性统计量中，我们看到沪深 300 指数日收益的偏度（Skewness）和峰度（Kurtosis）分别为 -0.118788 和 7.015960，表现出一定的左偏和明显的尖峰厚尾的特征（注：正态分布的偏度为 0，峰度为 3）。JB 统计量为 967.0165，其 p 值为 0，这也显著拒绝了沪深 300 指数日收益为正态分布的零假设。我们也可以从图 4 和图 5 中得到非正态分布的直观的验证。图 4 是沪深 300 指数日收益率的经验分布密度图，表现出明显的尖峰特征。图 5 是沪深 300 指数日收益率对正态分布的 Q-Q 图，它呈 S 形，与正态分布的为一条直线形成对比，也表明它呈尖峰厚尾特征。综上所有分析，沪深 300 指数日收益数据不服从正态分布，而是左偏、尖峰厚尾的，更接近于 t 分布。其中左偏表明总体来说，比较大的收益大多为负；尖峰厚尾表明有很多样本值较大幅度偏离均值，即金融市场由于利多利空消息波动较为剧烈，经常大起大落，从而有很多比较大的正收益和负收益。 3.2 弱平稳性（Weak Stability）如果一个随机过程的均值和方差在时间过程上都是常数，并且在任何两时期的协方差值仅依赖于该两时期间的距离或滞后，而不依赖于计算这个协方差的实际时间，就称它为弱平稳的。平稳性是比较重要的概念，因为一个序列是否平稳，冲击（Shock）对它的影响是不同的（逐步衰减或无限期持续下去）。如果它是不平稳的，运用计量模型对其进行回归就可能会导致“伪回归”（Spurious Regression）问题，并且由于此时 t 统计量不再遵循 t 分布、 F 统计量不再遵循 F 分布，以往的假设检验也可能不再有效。 1  Y t Y t 通常用 ADF 来检验时间序列是否存在单位根从而说明它是否平稳，检验的一般方程为： tu t  ，零假设为 H0∶ 1 , 备择假设为 H1∶ 1 。如果 H0 成立, 就      tY 意味着存在单位根，是非平稳序列（也叫 I(1)过程）；反之，若拒绝 H0 ，则就不存在单位根，从而是一个平稳的时间序列。 tY - 4 -

中国科技论文在线 http://www.paper.edu.cn 从图 6 的关于沪深 300 指数日收益率的 ADF 检验结果可以看到 t 统计值为-37.05689， p=0，说明 t 统计值显著小于 1%、5%和 10%显著性水平下的临界值，所以拒绝零假设，即不存在单位根，也即沪深 300 指数取对数差分得到的日收益率是平稳的。 3.3 序列相关性（Serial Correlation）由于经济变量固有的惯性、滞后效应、模型设定偏误等原因，往往会产生序列相关性，特别是经常出现在以时间序列数据为样本的模型中。当存在序列相关性时，就会使得参数估计量非有效，变量的显著性检验失去意义。所以我们对沪深 300 指数日收益率数据做一阶自相关检验，得出 D.W 统计量为 1.964802，接近 2，说明没有证据表明其存在自相关。我们也可以从图 7 的 10 阶滞后的 AC 和 PAC 图中看到除了第 3 阶和第 6 阶比相关系数为 0 的 2 倍标准差边界 2 / T 2 / T  小，这也说明了沪深 300 指数日收益率残差间不存在明显的自相关现象。）略大外，其它所有阶数都比（T 为 1435，所以 2 /   T   0.0528 图 1：沪深 300 指数走势图（2002/1/7~2007/12/14）图 2：沪深 300 指数日收益率波动图（2002/1/7~2007/12/14） - 5 -

中国科技论文在线 http://www.paper.edu.cn 图 3：沪深 300 指数日收益率描述性统计量（2002/1/7~2007/12/14）图 4：沪深 300 指数日收益率的经验分布密度图（2002/1/7~2007/12/14）图 5：沪深 300 指数日收益率对正态分布的 Q-Q 图图 6：沪深 300 指数日收益率的 ADF 检验 - 6 -

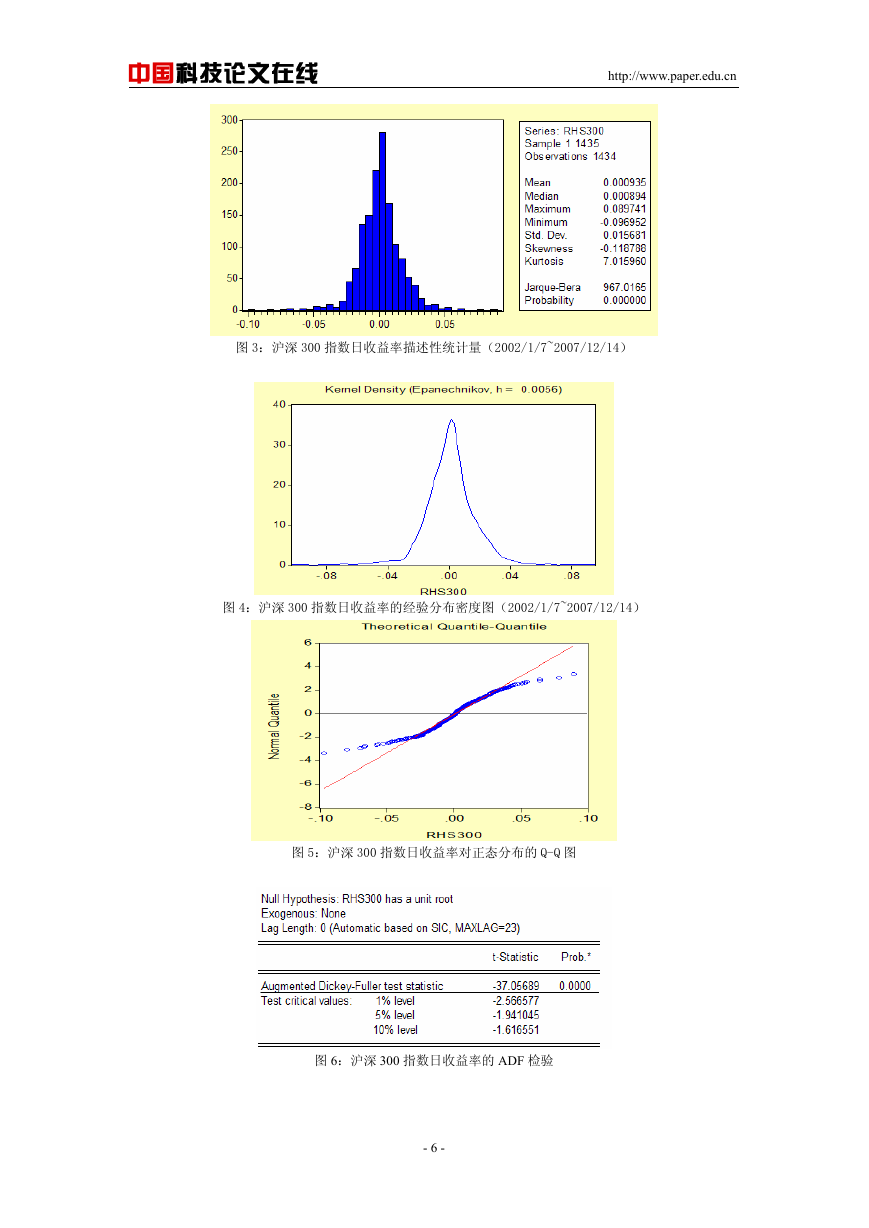
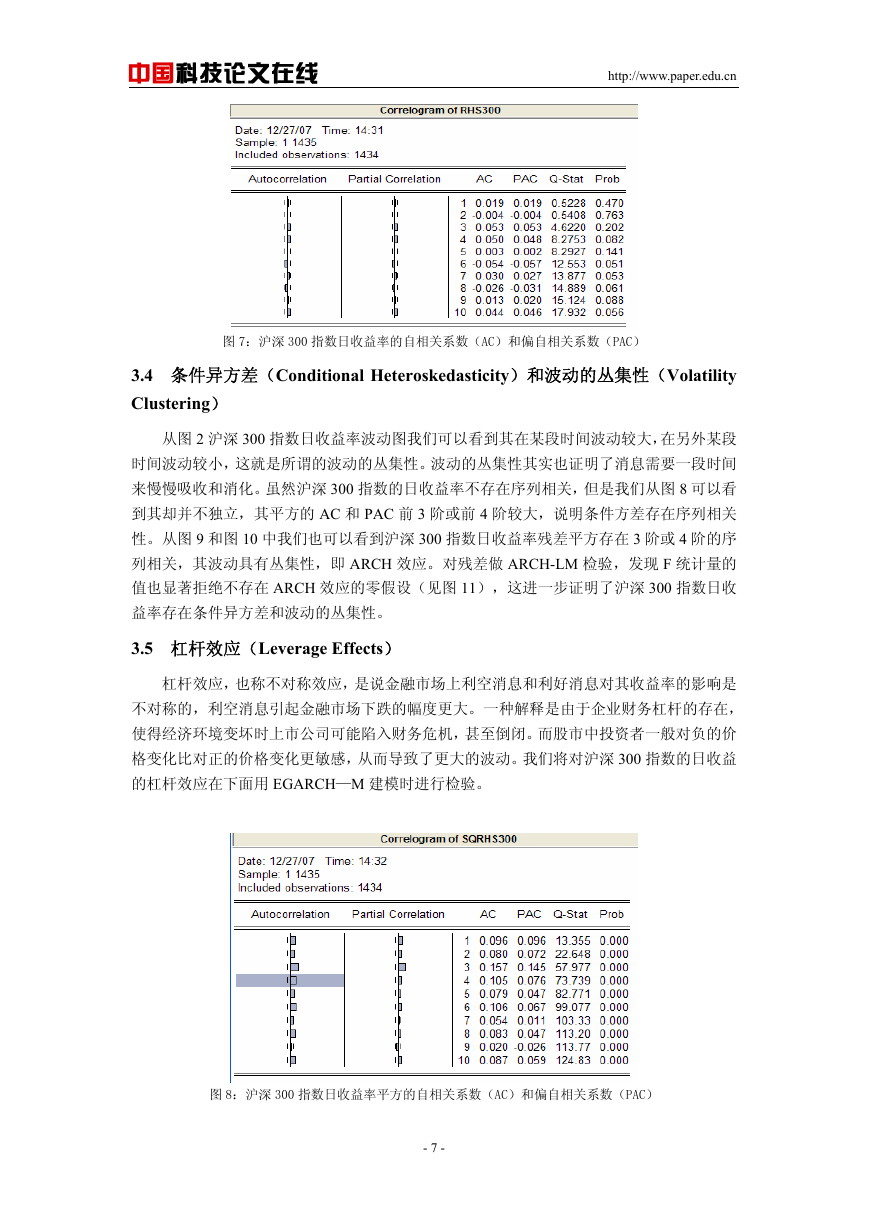
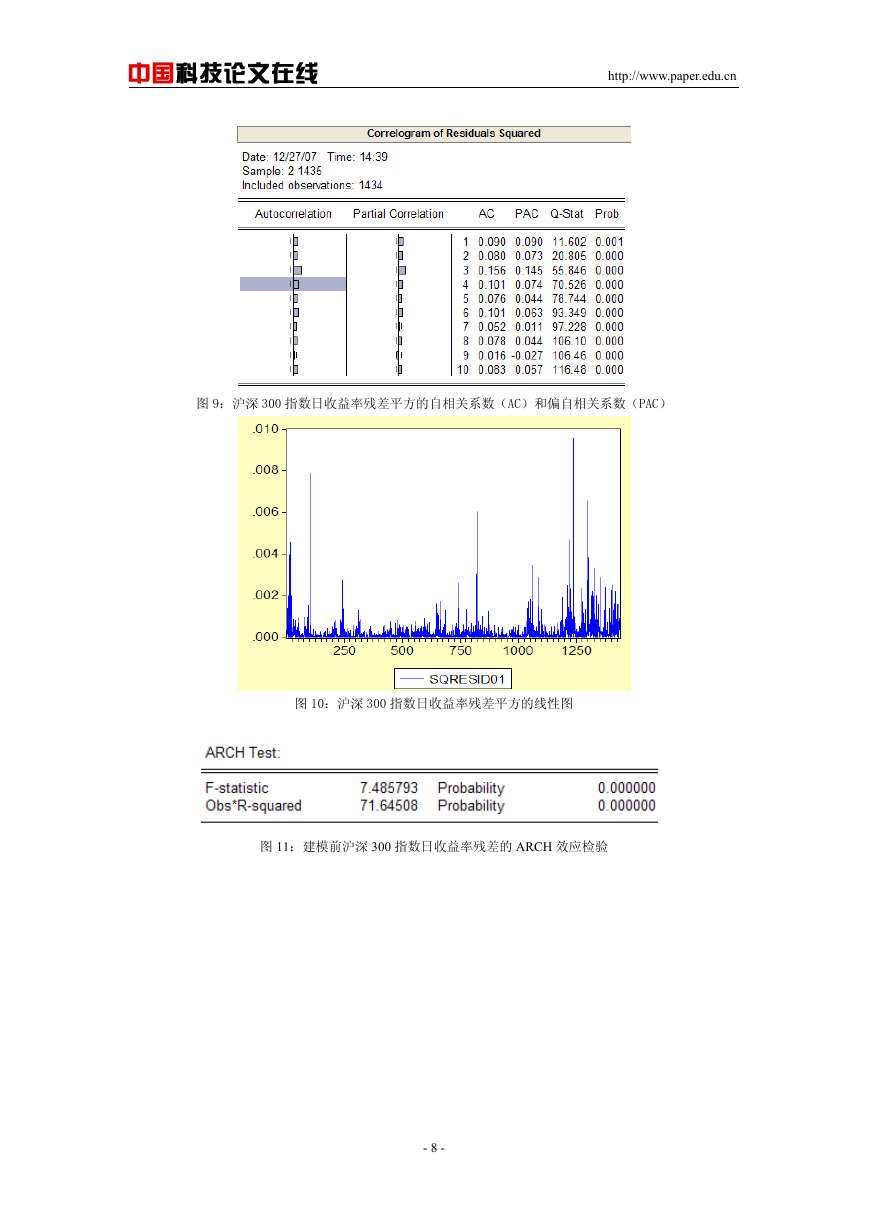
中国科技论文在线 http://www.paper.edu.cn 图 7：沪深 300 指数日收益率的自相关系数（AC）和偏自相关系数（PAC） 3.4 条件异方差（Conditional Heteroskedasticity）和波动的丛集性（Volatility Clustering）从图 2 沪深 300 指数日收益率波动图我们可以看到其在某段时间波动较大，在另外某段时间波动较小，这就是所谓的波动的丛集性。波动的丛集性其实也证明了消息需要一段时间来慢慢吸收和消化。虽然沪深 300 指数的日收益率不存在序列相关，但是我们从图 8 可以看到其却并不独立，其平方的 AC 和 PAC 前 3 阶或前 4 阶较大，说明条件方差存在序列相关性。从图 9 和图 10 中我们也可以看到沪深 300 指数日收益率残差平方存在 3 阶或 4 阶的序列相关，其波动具有丛集性，即 ARCH 效应。对残差做 ARCH-LM 检验，发现 F 统计量的值也显著拒绝不存在 ARCH 效应的零假设（见图 11），这进一步证明了沪深 300 指数日收益率存在条件异方差和波动的丛集性。 3.5 杠杆效应（Leverage Effects）杠杆效应，也称不对称效应，是说金融市场上利空消息和利好消息对其收益率的影响是不对称的，利空消息引起金融市场下跌的幅度更大。一种解释是由于企业财务杠杆的存在，使得经济环境变坏时上市公司可能陷入财务危机，甚至倒闭。而股市中投资者一般对负的价格变化比对正的价格变化更敏感，从而导致了更大的波动。我们将对沪深 300 指数的日收益的杠杆效应在下面用 EGARCH—M 建模时进行检验。图 8：沪深 300 指数日收益率平方的自相关系数（AC）和偏自相关系数（PAC） - 7 -

中国科技论文在线 http://www.paper.edu.cn 图 9：沪深 300 指数日收益率残差平方的自相关系数（AC）和偏自相关系数（PAC）图 10：沪深 300 指数日收益率残差平方的线性图图 11：建模前沪深 300 指数日收益率残差的 ARCH 效应检验 - 8 -

分享到：

赞收藏

资料库

沪深300指数日收益率时间序列特征分析.pdf

相关推荐

开发技术

热门标签

最新资料