DDE延迟微分方程数值算法（常量延迟）.pdf

发布时间：2022-06-03 发布人：admin 分类：说明书资料大小：0.08M 资料格式：pdf 举报版权申诉

krastin-6436251-16359647551100918191.pdf-第1页.png

第1页 / 共25页

krastin-6436251-16359647551100918191.pdf-第2页.png

第2页 / 共25页

krastin-6436251-16359647551100918191.pdf-第3页.png

第3页 / 共25页

krastin-6436251-16359647551100918191.pdf-第4页.png

第4页 / 共25页

krastin-6436251-16359647551100918191.pdf-第5页.png

第5页 / 共25页

krastin-6436251-16359647551100918191.pdf-第6页.png

第6页 / 共25页

krastin-6436251-16359647551100918191.pdf-第7页.png

第7页 / 共25页

krastin-6436251-16359647551100918191.pdf-第8页.png

第8页 / 共25页

Delay Differential Equations

Analytical Solutions and Stability

Example

History

Solving DDEs in extsc {Matlab}

$T^prime (t) = T(t) - 2,T(t - 1)$

Output of Program

Coding the DDEs

Method of Steps

Propagation of Discontinuities

Discontinuity Tree

Special Discontinuities

Runge--Kutta (RK) Formulas

Continuous Extensions

``Short'' Lags

Solution Structure

Rocking Suitcase

Nested Function for DDEs

Event Location

Nested Function for Events

Program, Part I

Program, Part II

Program, Part III

Output

Delay Differential Equations Part I: Constant Lags L.F. Shampine Department of Mathematics Southern Methodist University Dallas, Texas 75275 shampine@smu.edu www.faculty.smu.edu/shampine

Delay Differential Equations Delay differential equations (DDEs) with constant lags τj > 0 for j = 1, . . . , k have the form y′(t) = f (t, y(t), y(t − τ1), . . . , y(t − τk)) An early model of the El Niño/Southern Oscillation phenomenon with a physical parameter α > 0 is T ′(t) = T (t) − αT (t − τ ) A nonlinear ENSO model with periodic forcing is h′(t) = −a tanh[κ h(t − τ )] + b cos(2π ω t)

Analytical Solutions and Stability Linear, homogeneous, constant-coefﬁcient ODEs have solutions of the form y(t) = eλt. Any root λ of the characteristic equation provides a solution. This polynomial equation has a ﬁnite number of roots. The characteristic equation for linear, homogeneous, constant-coefﬁcient DDEs is transcendental. Generally there are inﬁnitely many roots λ. El’sgol’ts and Norkin give asymptotic expressions for these roots. The differential equation is stable if all roots of the characteristic equation satisfy Re(λ) ≤ β < 0. It is unstable if for some root, Re(λ) > 0.

Example Substituting y(t) = eλt into the neutral DDE y′(t) = y′(t − 1) + y(t) − y(t − 1) leads ﬁrst to λeλt = λeλt−λ + eλt − eλt−λ and then to the characteristic equation (λ − 1)1 − e−λ = 0 The roots are 1 and 2πi n for integer n. cos(2πnt) and sin(2πnt) are solutions for any integer n.

History An initial value y(a) = φ(a) is not enough to deﬁne a unique solution of y′(t) = f (t, y(t), y(t − τ1), . . . , y(t − τk)) on an interval a ≤ t ≤ b. We must specify y(t) = φ(t) for t ≤ a so that y(t − τj) is deﬁned when a ≤ t ≤ a + τj. The function φ(t) is called the history of the solution. The Fortran 90 program dde_solver and the two MATLAB programs allow the history argument to be provided as either a constant vector or a function.

Solving DDEs in MATLAB dde23 solves DDEs with constant lags on [a, b]. This is much like solving ODEs with ode23, but • You must input the lags and the history. • The end points must satisfy a < b. • Output is always in the form of a solution structure. • Solution values are available at mesh points as ﬁelds in the structure and anywhere in a ≤ t ≤ b using deval.

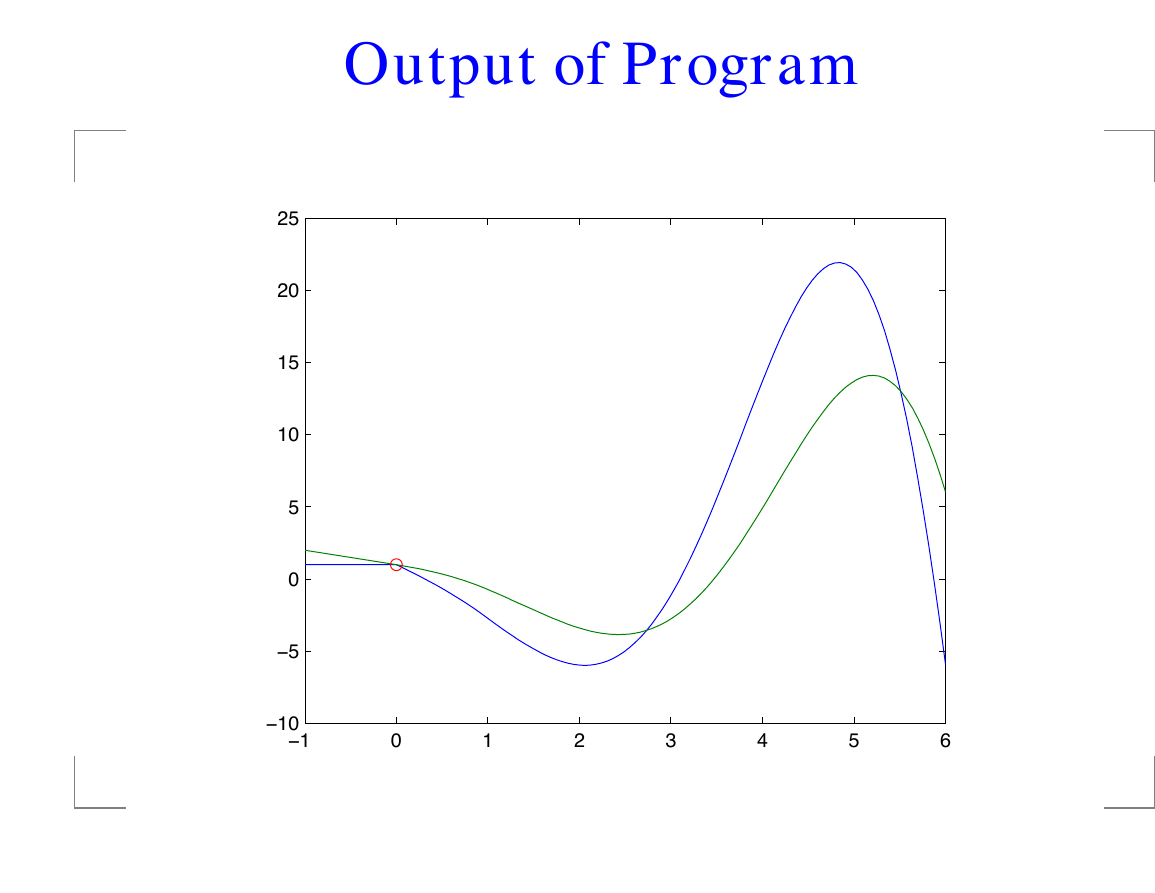
T ′(t) = T (t) − 2 T (t − 1) function Ex1 lags = 1; tspan = [0 6]; sol1 = dde23(@dde,lags,@history,tspan); sol2 = dde23(@dde,lags,1,tspan); tplot = linspace(0,6,100); T1 = deval(sol1,tplot); T2 = deval(sol2,tplot); tplot = [-1 tplot]; T1 = [1 T1]; T2 = [2 T2]; plot(tplot,T1,tplot,T2,0,1,’o’) %--Subfunctions--------------------- function dydt = dde(t,T,Z) dydt = T - 2*Z; function s = history(t) s = 1 - t;

Output of Program 25 20 15 10 5 0 −5 −10 −1 0 1 2 3 4 5 6

分享到：

赞收藏

资料库

DDE延迟微分方程数值算法（常量延迟）.pdf

相关推荐

行业

热门标签

最新资料