第1页 / 共447页
第2页 / 共447页
第3页 / 共447页
第4页 / 共447页
第5页 / 共447页
第6页 / 共447页
第7页 / 共447页
第8页 / 共447页
计算神经学教材 Theoretical Neuroscience.pdf
Cover
Preface
1. Neural Encoding I: Firing Rates and Spike Statistics
1.7 Appendices
1.6 Chapter Summary
1.5 The Neural Code
1.4 Spike Train Statistics
1.3 What Makes a Neuron Fire
1.2 Spike Trains and Firing Rates
1.1 Introduction
2. Neural Encoding II: Reverse Correlation and Visual Receptive Fields
2.10 Annotated Bibliography
2.9 Appendices
2.8 Chapter Summary
2.7 Constructing V1 Receptive Fields
2.6 Receptive Fields in the Retina and LGN
2.5 Static Nonlinearities - Complex Cells
2.4 Reverse Correlation Methods - Simple Cells
2.3 Introduction to the Early Visual System
2.2 Estimating Firing Rates
2.1 Introduction
3. Neural Decoding
3.7 Annotated Bibliography
3.6 Appendices
3.5 Chapter Summary
3.4 Spike Train Decoding
3.3 Population Decoding
3.2 Discrimination
3.1 Encoding and Decoding
4. Information Theory
4.6 Annotated Bibliography
4.4 Chapter Summary
4.3 Entropy and Information for Spike Trains
4.2 Information and Entropy Maximization
4.1 Entropy and Mutual Information
4.5 Appendices
5. Model Neurons I: Neuroelectronics
5.2 Electrical Properties of Neurons
5.8 Synaptic Conductances
5.12 Annotated Bibliography
5.11 Appendices
5.10 Chapter Summary
5.9 Synapses on Integrate-and-Fire Neurons
5.7 Modeling Channels
5.6 The Hodgkin-Huxley Model
5.5 Voltage-Dependent Conductances
5.4 Integrate-and-Fire Models
5.3 Single-Compartment Models
5.1 Introduction
6. Model Neurons II: Conductances and Morphology
6.7 Annotated Bibliography
6.6 Appendices
6.5 Chapter Summary
6.4 Multi-Compartment Models
6.3 The Cable Equation
6.2 Conductance-Based Models
6.1 Levels of Neuron Modeling
7. Network Models
7.8 Annotated Bibliography
Appendix
7.7 Chapter Summary
7.6 Stochastic Netoworks
7.5 Excitatory-Inhibitory Networks
7.4 Recurrent Networks
7.3 Feedforward Networks
7.2 Firing-Rate Models
7.1 Introduction
8. Plasticity and Learning
8.7 Annotated Bibliography
8.6 Appendix
8.5 Chapter Summary
8.4 Supervised Learning
8.3 Unsupervised Learning
8.2 Synaptic Plasticity Rules
8.1 Introduction
9. Classical Conditioning and Reinforcement Learning
9.1 Introduction
9.2 Classical Conditioning
9.3 Static Action Choice
9.4 Sequential Action Choice
9.5 Chapter Summary
Appendix
9.6 Annotated Bibliography
10. Representational Learning
10.1 Introduction
10.2 Density Estimation
10.3 Causal Models for Density Estimation
10.4 Discussion
10.5 Chapter Summary
10.6 Appendix
10.7 Annotated Bibliography
Exercises
Chapter 2
Chapter 3
Chapter 4
Chapter 5
Chapter 1
Mathematical Appendix
Linear Algebra
Functional Analogs
Eigenvectors and Eigenvalues
Fourier Transforms
Finding Extrema and Lagrange Multipliers
Differential Equations
Electrical Circuits
Probability Theory
Annotated Bibliography
References
Preface
Theoretical analysis and computational modeling are important tools for
characterizing what nervous systems do, determining how they function,
and understanding why they operate in particular ways. Neuroscience
encompasses approaches ranging from molecular and cellular studies to
human psychophysics and psychology. Theoretical neuroscience encour-
ages cross-talk among these sub-disciplines by constructing compact rep-
resentations of what has been learned, building bridges between different
levels of description, and identifying unifying concepts and principles. In
this book, we present the basic methods used for these purposes and dis-
cuss examples in which theoretical approaches have yielded insight into
nervous system function.
The questions what, how, and why are addressed by descriptive, mecha-
nistic, and interpretive models, each of which we discuss in the following
chapters. Descriptive models summarize large amounts of experimental
data compactly yet accurately, thereby characterizing what neurons and
neural circuits do. These models may be based loosely on biophysical,
anatomical, and physiological findings, but their primary purpose is to de-
scribe phenomena not to explain them. Mechanistic models, on the other mechanistic models
hand, address the question of how nervous systems operate on the ba-
sis of known anatomy, physiology, and circuitry. Such models often form
a bridge between descriptive models couched at different levels.
Inter-
pretive models use computational and information-theoretic principles to interpretive models
explore the behavioral and cognitive significance of various aspects of ner-
vous system function, addressing the question of why nervous system op-
erate as they do.
descriptive models
It is often difficul to identify the appropriate level of modeling for a partic-
ular problem. A frequent mistake is to assume that a more detailed model
is necessarily superior. Because models act as bridges between levels of
understanding, they must be detailed enough to make contact with the
lower level yet simple enough to yield clear results at the higher level.
Draft: December 17, 2000
Theoretical Neuroscience
2
Organization and Approach
This book is organized into three parts on the basis of general themes.
Part I (chapters 1-4) is devoted to the coding of information by action
potentials and the represention of information by populations of neurons
with selective responses. Modeling of neurons and neural circuits on the
basis of cellular and synaptic biophysics is presented in part II (chapters
5-7). The role of plasticity in development and learning is discussed in
Part III (chapters 8-10). With the exception of chapters 5 and 6, which
jointly cover neuronal modeling, the chapters are largely independent and
can be selected and ordered in a variety of ways for a one- or two-semester
course at either the undergraduate or graduate level.
Although we provide some background material, readers without previ-
ous exposure to neuroscience should refer to a neuroscience textbook such
as Kandel, Schwartz & Jessell (2000); Nicholls, Martin & Wallace (1992);
Bear, Connors & Paradiso (1996); Shepherd (1997); Zigmond, Bloom, Lan-
dis & Squire (1998); Purves et al (2000).
Theoretical neuroscience is based on the belief that methods of mathemat-
ics, physics, and computer science can elucidate nervous system function.
Unfortunately, mathematics can sometimes seem more of an obstacle than
an aid to understanding. We have not hesitated to employ the level of
analysis needed to be precise and rigorous. At times, this may stretch the
tolerance of some of our readers. We encourage such readers to consult
the mathematical appendix, which provides a brief review of most of the
mathematical methods used in the text, but also to persevere and attempt
to understand the implications and consequences of a difficult derivation
even if its steps are unclear.
Theoretical neuroscience, like any skill, can only be mastered with prac-
tice. We have provided exercises for this purpose on the web site for this
book and urge the reader to do them. In addition, it will be highly in-
structive for the reader to construct the models discussed in the text and
explore their properties beyond what we have been able to do in the avail-
able space.
Referencing
In order to maintain the flow of the text, we have kept citations within
the chapters to a minimum. Each chapter ends with an annotated bib-
liography containing suggestions for further reading (which are denoted
by a bold font), information about work cited within the chapter, and ref-
erences to related studies. We concentrate on introducing the basic tools
of computational neuroscience and discussing applications that we think
best help the reader to understand and appreciate them. This means that
a number of systems where computational approaches have been applied
Peter Dayan and L.F. Abbott
Draft: December 17, 2000
3
with significant success are not discussed. References given in the anno-
tated bibliographies lead the reader toward such applications.
In most
of the areas we cover, many people have provided critical insights. The
books and review articles in the further reading category provide more
comprehensive references to work that we apologetically have failed to
cite.
Acknowledgments
We are extremely grateful to a large number of students at Brandeis,
the Gatsby Computational Neuroscience Unit and MIT, and colleagues
at many institutions, who have painstakingly read, commented on, and
criticized, numerous versions of all the chapters. We particularly thank
Bard Ermentrout, Mark Kvale, Mark Goldman, John Hertz, Zhaoping
Li, Eve Marder, and Read Montague for providing extensive discussion
and advice on the whole book. A number of people read significant
portions of the text and provided valuable comments, criticism, and in-
sight: Bill Bialek, Pat Churchland, Nathanial Daw, Dawei Dong, Peter
F¨oldi´ak, Fabrizio Gabbiani, Zoubin Ghahramani, Geoff Goodhill, David
Heeger, Geoff Hinton, Ken Miller, Tony Movshon, Phil Nelson, Sacha Nel-
son, Bruno Olshausen, Mark Plumbley, Alex Pouget, Fred Rieke, John
Rinzel, Emilio Salinas, Sebastian Seung, Mike Shadlen, Satinder Singh,
Rich Sutton, Nick Swindale, Carl Van Vreeswijk, Chris Williams, David
Willshaw, Charlie Wilson, Angela Yu, and Rich Zemel. We have received
significant additional assistance and advice from: Greg DeAngelis, Matt
Beal, Sue Becker, Tony Bell, Paul Bressloff, Emery Brown, Matteo Caran-
dini, Frances Chance, Yang Dan, Kenji Doya, Ed Erwin, John Fitzpatrick,
David Foster, Marcus Frean, Ralph Freeman, Enrique Garibay, Frederico
Girosi, Charlie Gross, Mike Jordan, Sham Kakade, Szabolcs K´ali, Christof
Koch, Simon Laughin, John Lisman, Shawn Lockery, Guy Mayraz, Quaid
Morris, Randy O’Reilly, Max Riesenhuber, Sam Roweis, Simon Osindero,
Tomaso Poggio, Clay Reid, Dario Ringach, Horacio Rotstein, Lana Ruther-
ford, Ken Sagino, Maneesh Sahani, Alexei Samsonovich, Idan Segev, Terry
Sejnowski, Haim Sompolinksy, Fiona Stevens, David Tank, Alessandro
Treves, Gina Turrigiano, David Van Essen, Martin Wainwright, Xiao-Jing
Wang, Max Welling, Matt Wilson, Danny Young, and Ketchen Zhang. We
apologise to anyone we may have inadvertently omitted from these lists.
Karen Abbott provided valuable help with the figures. From MIT Press,
we thank Michael Rutter for his patience and consistent commitment, and
Sara Meirowitz and Larry Cohen for picking up where Michael left off.
Draft: December 17, 2000
Theoretical Neuroscience
Chapter 1
Neural Encoding I: Firing
Rates and Spike Statistics
1.1
Introduction
Neurons are remarkable among the cells of the body in their ability to
propagate signals rapidly over large distances. They do this by generat-
ing characteristic electrical pulses called action potentials, or more simply
spikes, that can travel down nerve fibers. Neurons represent and transmit
information by firing sequences of spikes in various temporal patterns.
The study of neural coding, which is the subject of the first four chapters of
this book, involves measuring and characterizing how stimulus attributes,
such as light or sound intensity, or motor actions, such as the direction of
an arm movement, are represented by action potentials.
The link between stimulus and response can be studied from two opposite
points of view. Neural encoding, the subject of chapters 1 and 2, refers to
the map from stimulus to response. For example, we can catalogue how
neurons respond to a wide variety of stimuli, and then construct models
that attempt to predict responses to other stimuli. Neural decoding refers
to the reverse map, from response to stimulus, and the challenge is to re-
construct a stimulus, or certain aspects of that stimulus, from the spike
sequences it evokes. Neural decoding is discussed in chapter 3. In chapter
4, we consider how the amount of information encoded by sequences of
action potentials can be quantified and maximized. Before embarking on
this tour of neural coding, we briefly review how neurons generate their
responses and discuss how neural activity is recorded. The biophysical
mechanisms underlying neural responses and action potential generation
are treated in greater detail in chapters 5 and 6.
Draft: December 17, 2000
Theoretical Neuroscience
2
Neural Encoding I: Firing Rates and Spike Statistics
Properties of Neurons
Neurons are highly specialized for generating electrical signals in response
to chemical and other inputs, and transmitting them to other cells. Some
important morphological specializations, seen in the drawings of figure
1.1, are the dendrites that receive inputs from other neurons and the axon
that carries the neuronal output to other cells. The elaborate branching
structure of the dendritic tree allows a neuron to receive inputs from many
other neurons through synaptic connections. The cortical pyramidal neu-
ron of figure 1.1A and the cortical interneuron of figure 1.1C each receives
thousands of synaptic inputs, and for the cerebellar Purkinje cell of figure
1.1B the number is over 100,000. Figure 1.1 does not show the full extent of
the axons of these neurons. Axons from single neurons can traverse large
fractions of the brain or, in some cases, of the entire body. In the mouse
brain, it has been estimated that cortical neurons typically send out a total
of about 40 mm of axon and have approximately 4 mm of total dendritic
cable in their branched dendritic trees. The axon makes an average of 180
synaptic connections with other neurons per mm of length while the den-
dritic tree receives, on average, 2 synaptic inputs per µm. The cell body or
soma of a typical cortical neurons ranges in diameter from about 10 to 50
µm.
+
Along with these morphological features, neurons have physiological
specializations. Most prominent among these are a wide variety of
membrane-spanning ion channels that allow ions, predominantly sodium
(Na
), to move into
and out of the cell. Ion channels control the flow of ions across the cell
membrane by opening and closing in response to voltage changes and
both internal and external signals.
−
), and chloride (Cl
+
), potassium (K
), calcium (Ca2+
The electrical signal of relevance to the nervous system is the difference
in electrical potential between the interior of a neuron and the surround-
ing extracellular medium. Under resting conditions, the potential inside
the cell membrane of a neuron is about -70 mV relative to that of the sur-
rounding bath (which is conventionally defined to be 0 mV), and the cell
is said to be polarized. Ion pumps located in the cell membrane maintain
concentration gradients that support this membrane potential difference.
+
For example, Na
is much more concentrated outside a neuron than in-
+
side it, and the concentration of K
is significantly higher inside the neu-
ron than in the extracellular medium.
Ions thus flow into and out of a
cell due to both voltage and concentration gradients. Current, in the form
of positively charged ions flowing out of the cell (or negatively charged
ions flowing into the cell) through open channels makes the membrane
potential more negative, a process called hyperpolarization. Current flow-
ing into the cell changes the membrane potential to less negative or even
positive values. This is called depolarization.
If a neuron is depolarized sufficiently to raise the membrane potential
above a threshold level, a positive feedback process is initiated, and the
Peter Dayan and L.F. Abbott
Draft: December 17, 2000
axons and
dendrites
ion channels
membrane
potential
hyperpolarization
and depolarization
1.1 Introduction
3
A
apical
dendrite
B
dendrite
soma
basal
dendrite
C
dendrite
axon
collaterals
axon
soma
axon
axon
soma
Figure 1.1: Diagrams of three neurons. A) A cortical pyramidal cell. These are
the primary excitatory neurons of the cerebral cortex. Pyramidal cell axons branch
locally, sending axon collaterals to synapse with nearby neurons, and also project
more distally to conduct signals to other parts of the brain and nervous system.
B) A Purkinje cell of the cerebellum. Purkinje cell axons transmit the output of
the cerebellar cortex. C) A stellate cell of the cerebral cortex. Stellate cells are
one of a large class of cells that provide inhibitory input to the neurons of the
cerebral cortex. To give an idea of scale, these figures are magnified about 150 fold.
(Drawings from Cajal, 1911; figure from Dowling, 1992.)
neuron generates an action potential. An action potential is a roughly 100
mV fluctuation in the electrical potential across the cell membrane that
lasts for about 1 ms (figure 1.2A). Action potential generation also depends
on the recent history of cell firing. For a few milliseconds just after an
action potential has been fired, it may be virtually impossible to initiate
another spike. This is called the absolute refractory period. For a longer
interval known as the relative refractory period, lasting up to tens of mil-
liseconds after a spike, it is more difficult to evoke an action potential.
action potential
refractory period
Draft: December 17, 2000
Theoretical Neuroscience
4
A
)
V
m
(
l
a
i
t
n
e
t
o
p
e
n
a
r
b
m
e
m
20
0
-20
-40
-60
0
Neural Encoding I: Firing Rates and Spike Statistics
B
axon terminal
of presynaptic
neuron
dendritic
specialization
dendrite
microtubules
mitochondrion
synaptic
vesicles
cleft
dendritic spine
of postsynaptic
neuron
100
time (ms)
200
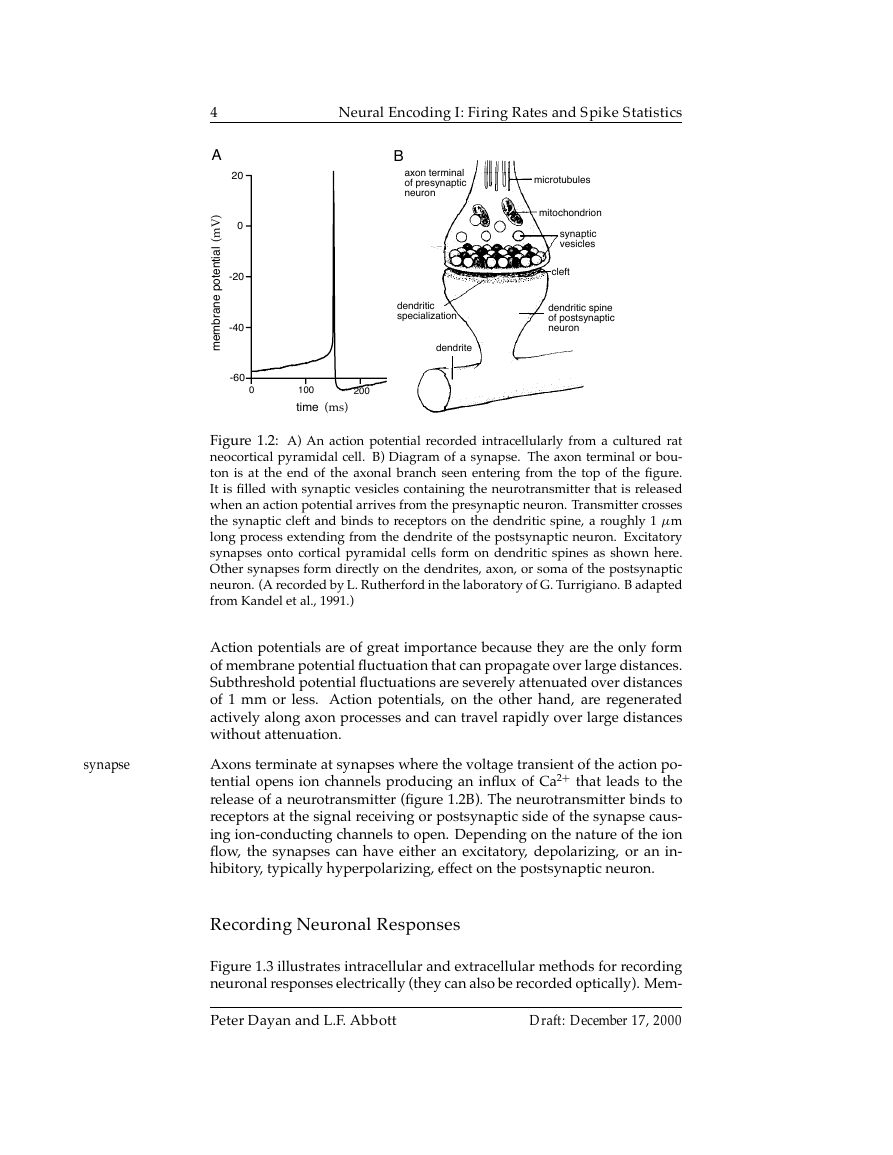
Figure 1.2: A) An action potential recorded intracellularly from a cultured rat
neocortical pyramidal cell. B) Diagram of a synapse. The axon terminal or bou-
ton is at the end of the axonal branch seen entering from the top of the figure.
It is filled with synaptic vesicles containing the neurotransmitter that is released
when an action potential arrives from the presynaptic neuron. Transmitter crosses
the synaptic cleft and binds to receptors on the dendritic spine, a roughly 1 µm
long process extending from the dendrite of the postsynaptic neuron. Excitatory
synapses onto cortical pyramidal cells form on dendritic spines as shown here.
Other synapses form directly on the dendrites, axon, or soma of the postsynaptic
neuron. (A recorded by L. Rutherford in the laboratory of G. Turrigiano. B adapted
from Kandel et al., 1991.)
Action potentials are of great importance because they are the only form
of membrane potential fluctuation that can propagate over large distances.
Subthreshold potential fluctuations are severely attenuated over distances
of 1 mm or less. Action potentials, on the other hand, are regenerated
actively along axon processes and can travel rapidly over large distances
without attenuation.
Axons terminate at synapses where the voltage transient of the action po-
tential opens ion channels producing an influx of Ca2+
that leads to the
release of a neurotransmitter (figure 1.2B). The neurotransmitter binds to
receptors at the signal receiving or postsynaptic side of the synapse caus-
ing ion-conducting channels to open. Depending on the nature of the ion
flow, the synapses can have either an excitatory, depolarizing, or an in-
hibitory, typically hyperpolarizing, effect on the postsynaptic neuron.
Recording Neuronal Responses
Figure 1.3 illustrates intracellular and extracellular methods for recording
neuronal responses electrically (they can also be recorded optically). Mem-
Peter Dayan and L.F. Abbott
Draft: December 17, 2000
synapse
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
