α 1997 年 5 月 系统工程理论与实践 第 5 期 M GM (1, n) 灰色模型及应用 翟 军　　　　　　　　盛建明 (哈尔滨工业大学数学系, 150001) 　　 (石油勘探开发科学研究院, 北京 100083) 冯英浚 (哈尔滨工业大学数学系, 150001) 摘要　提出多变量灰色模型 (m u lti variab le grey model) —M GM (1, n) 模型, 它是单变量的 GM (1, 1) 模型在多变量 ( n 元变量) 情况下的自然推广。通过对国有建筑施工企业就业人数和城镇集体建筑 施工企业就业人数的建模和预测, 表明M GM (1, n) 模型的精度高于分别单独使用的 GM (1, 1) 模型 的精度。 关键词　M GM (1, n) 模型　GM (1, 1) 模型　建模　预测 T he Grey M odel M GM (1, n) and Its A pp lication Zhai J un (D ep t. of M ath. , H arb in In stitu te of T echno logy, H arb in 150001) Sheng J ianm ing (R esearch In stitu te of Petro leum Exp lo ration and D evelopm en t,B eijing 100083) Feng Y ing jun (D ep t. of M ath. , H arb in In stitu te of T echno logy, H arb in 150001) Abstract 　 In th is paper, a m u lti- variab le grey m odel (M GM (1, n) ) is p resen ted, w h ich generalizes the un ivariab le GM (1, 1) m odel to the m u lti- variab le system. A p ractice exam p le is given abou t the to tal em p loyees of national operated and u rban co l lective arch itectu ral en terp rises, in w h ich a com parison abou t the m odeling and p redic tion resu lts is m ade betw een tw o cases: u sing the M GM (1, n) m odel on ly and u sing the GM (1, 1) seperately. Keywords　M GM (1, n) ; GM (1, 1) ; m odeling; p rediction It is show n the M GM (1, n) m odel has a h igher accu racy. 1　前言 GM (1, 1) 模型是最常用的一种灰色系统模型[1 ], 它通过单变量的一阶微分方程模型揭示其内在发展 规律, 用于单一时间序列的建模和预测。 然而实际的社会、经济系统中往往包含多个变量。 各变量相互关 联、共同发展。 这时, 每一变量的发展变化都不是弧立的, 一个变量要受到其他变量的影响, 同时也影响着 其他变量。为此, 本文提出多变量灰色模型——M GM (1, n) 模型, 旨在从系统的角度对各变量进行统一描 述。M GM (1, n) 模型的形式是 n 元一阶常微分方程组, 它是 GM (1, 1) 模型在 n 元变量情况下的自然推广, 本文于 1995 年 11 月 20 日收到 

δ δ δ r δ δ 系统工程理论与实践 011 1997 年 5 月 不是 GM (1, 1) 模型的简单组合, 也不同于 GM (1, n) 模型。最后对国有建筑施工企业就业人数和城镇集体 建筑施工企业就业人数建立 GM (1, 2) 模型, 阐明了M GM (1, n) 模型的应用。 2　M GM (1, n) 模型 　　令 x (0) 即 (k) i, i (i= 1, 2, …, n) 为 n 个灰时间序列, x (1) i (k ) , ( i= 1, 2, …, n) 为相应的一次累加生成序列, 其中 k= 1, 2, …, m 。 M GM (1, n) 模型为 n 元一阶常微分方程组: x (1) i (k) = k j= 1 x (0) i (j ) d x (1) 1 d t d x (1) 2 d t = a11x (1) 1 + a12x (1) 2 + … + a1nx (1) n + b1 = a21x (1) 1 + a22x (1) 2 + … + a2nx (1) n + b2 　　　 d x (1) n d t = an1x (1) 1 + an2x (1) 2 + … + annx (1) n + bn 记 X (0) (k ) = (x (0) 1 X (1) (k ) = (x (1) 1 a11 a21 A = (k ) , x (0) 2 (k ) , x (1) 2 (k ) , …, x (0) (k ) , …, x (1) n n (k ) ) T , (k ) ) T , a12 … a1n a22 … a2n 则 (2) 式可记为 　　上式的连续时间响应为 [2 ] 其中 an1 an2 … ann B = (b1, b2, …, bn) T dX (1) d t = A X (1) + B X (1) (t) = eA tX (1) (0) + A - 1 (eA t - I ) B eA t= I + A t + A 2 2! t2 + … = I + ∞ k= 1 A k k ! tk (1) (2) (3) (4) 　　为辩识参数 A 和 B , 将 (2) 离散化得到 x (0) i (k ) = n j= 1 a ij 2 (x (1) j (k) + x (1) j (k - 1) ) + bi　　i = 1, 2, …, n; k = 2, 3, …, m (5) 　　记 a i= (a i1, a i2, …, a in, bi) T , i= 1, 2, …, n。 则由最小二乘法得到 a i 的辩识值 a i a i = a a i1 i2 a b in i = (L TL ) - 1L T Y i　　i = 1, 2, …, n (6) 

第 5 期 M GM (1, n) 灰色模型及应用 其中 L = 1 2 1 2 (x (1) 1 (2) + x (1) 1 (1) ) , (x (1) 1 (3) + x (1) 1 (2) ) , 1 2 1 2 (x (1) 2 (2) + x (1) 2 (1) ) , …, (x (1) 2 (3) + x (1) 2 (2) ) , …, 1 2 1 2 (x (1) n (2) + x (1) n (1) ) , (x (1) n (3) + x (1) n (2) ) , (m ) + x (1) 1 (x (1) 1 1 2 Y i= (x (0) i 则得 A 和 B 的辩识值 A (2) , x (0) i (3) , …, x (0) i 和 B (m 1) ) , 1 2 (x (1) 2 (m ) + x (1) 2 (m 1) ) , …, 1 2 (x (1) n (m ) + x (1) n (m 1) ) , (m ) ) T A = a a 11 21 12 … a 22 … a a a 1n 2n a n1 n2 … a a nn , 　　B = b 1 b 2 b n 111 1 1 1 (7) (8) 　　M GM (1, n) 模型的计算值为 (1) (k ) = eA (0) (1) = X (0) (1) (0) (k ) = X X X X (k- 1)X (1) (1) + A - 1 (eA (k- 1) - I ) B , 　　 k = 1, 2, … (9) 　　当 n= 1 时,M GM (1, n) 模型退化为 GM (1, 1) 模型; 当 B = 0 时,M GM (1, n) 模型为 n 个 GM (1, n) 模 型的组合。应该指出的是由公式 (4) , (8) 和 (9) 知M GM (1, n) 模型不仅可以建模, 而且可以预测, 而 GM (1, n) 模型仅仅是状态模型, 不能用于预测[1 ]。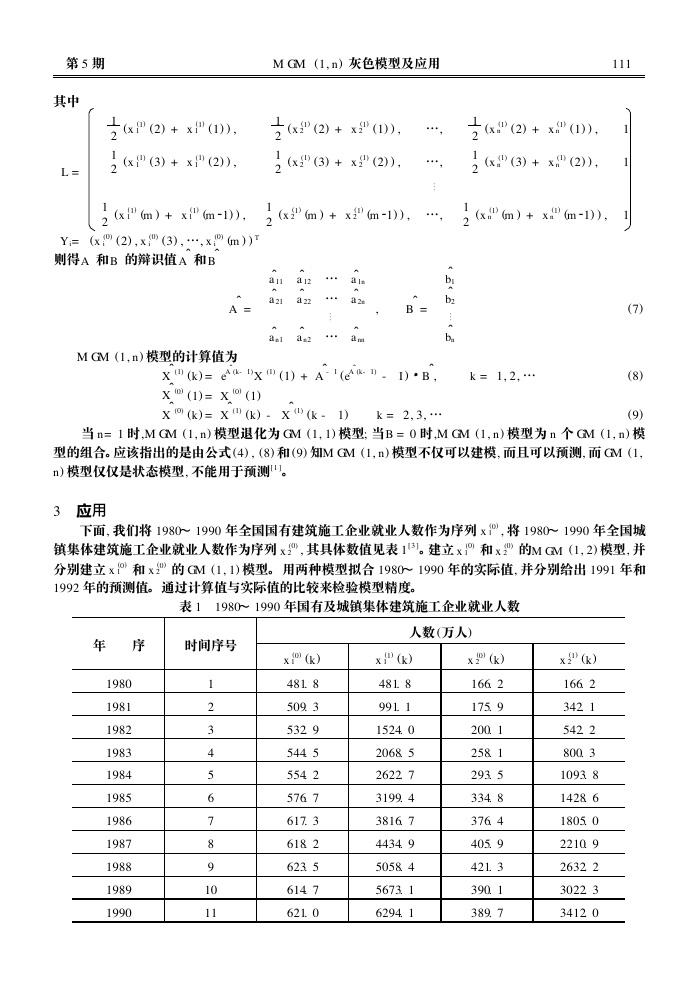 (1) (k - 1) 　　k = 2, 3, … (1) (k) - X 3　应用 下面, 我们将 1980～ 1990 年全国国有建筑施工企业就业人数作为序列 x (0) 1 , 将 1980～ 1990 年全国城 2 的M GM (1, 2) 模型, 并 2 的 GM (1, 1) 模型。 用两种模型拟合 1980～ 1990 年的实际值, 并分别给出 1991 年和 镇集体建筑施工企业就业人数作为序列 x (0) 2 分别建立 x (0) 1992 年的预测值。 通过计算值与实际值的比较来检验模型精度。 , 其具体数值见表 1 [3 ]。建立 x (0) 1 和 x (0) 1 和 x (0) 表 1　1980～ 1990 年国有及城镇集体建筑施工企业就业人数 年　　序 时间序号 1980 1981 1982 1983 1984 1985 1986 1987 1988 1989 1990 1 2 3 4 5 6 7 8 9 10 11 x (0) 1 (k ) 481. 8 509. 3 532. 9 544. 5 554. 2 576. 7 617. 3 618. 2 623. 5 614. 7 621. 0 人数 (万人) x (1) 1 (k ) 481. 8 991. 1 1524. 0 2068. 5 2622. 7 3199. 4 3816. 7 4434. 9 5058. 4 5673. 1 6294. 1 x (0) 2 (k) 166. 2 175. 9 200. 1 258. 1 293. 5 334. 8 376. 4 405. 9 421. 3 390. 1 389. 7 x (1) 2 (k ) 166. 2 342. 1 542. 2 800. 3 1093. 8 1428. 6 1805. 0 2210. 9 2632. 2 3022. 3 3412. 0 

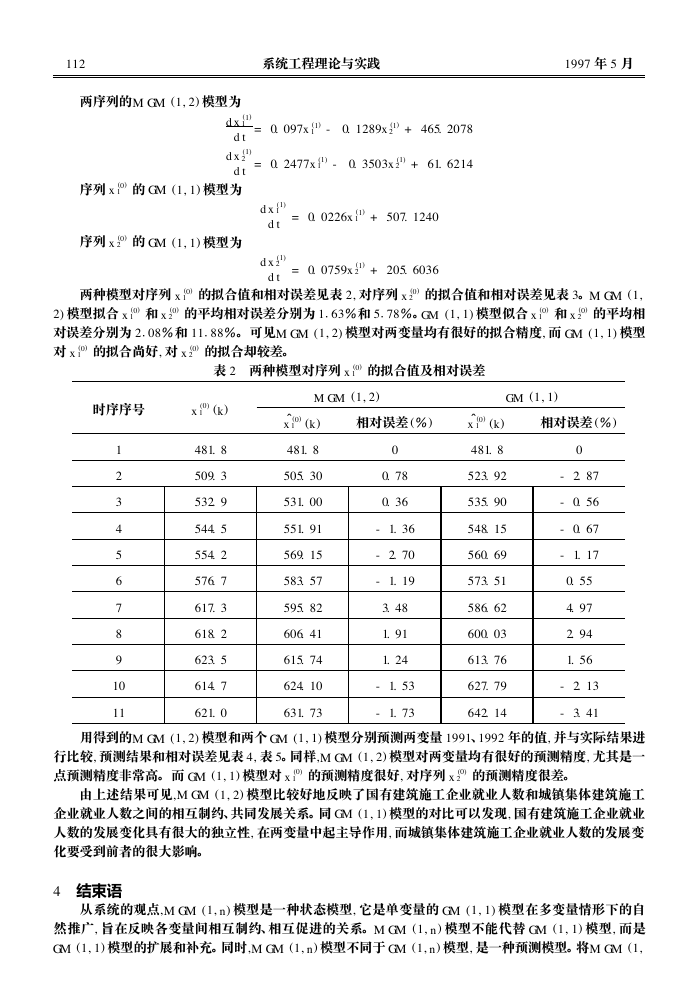
211 系统工程理论与实践 1997 年 5 月 　　两序列的M GM (1, 2) 模型为 d x (1) 1 d t d x (1) 2 d t 1 的 GM (1, 1) 模型为 　　序列 x (0) 　　序列 x (0) 2 的 GM (1, 1) 模型为 = 0. 097x (1) 1 - 0. 1289x (1) 2 + 465. 2078 = 0. 2477x (1) 1 - 0. 3503x (1) 2 + 61. 6214 d x (1) 1 d t d x (1) 2 d t = 0. 0226x (1) 1 + 507. 1240 = 0. 0759x (1) 2 + 205. 6036 　　两种模型对序列 x (0) 2) 模型拟合 x (0) 对误差分别为 2 对 x (0) 2 的平均相对误差分别为 1 和 11 1 的拟合尚好, 对 x (0) 2 的拟合却较差。 1 和 x (0) 88 08 78 1 的拟合值和相对误差见表 2, 对序列 x (0) 2 的拟合值和相对误差见表 3。M GM (1, 。GM (1, 1) 模型似合 x (0) 2 的平均相 。可见M GM (1, 2) 模型对两变量均有很好的拟合精度, 而 GM (1, 1) 模型 1 和 x (0) 和 5 63 表 2　两种模型对序列 x (0) 1 的拟合值及相对误差 时序序号 x (0) 1 (k) 1 2 3 4 5 6 7 8 9 10 11 481. 8 509. 3 532. 9 544. 5 554. 2 576. 7 617. 3 618. 2 623. 5 614. 7 621. 0 M GM (1, 2) GM (1, 1) (0) 1 x (k ) 481. 8 505. 30 531. 00 551. 91 569. 15 583. 57 595. 82 606. 41 615. 74 624. 10 631. 73 相对误差 ( ) 0 0. 78 0. 36 - 1. 36 - 2. 70 - 1. 19 3. 48 1. 91 1. 24 - 1. 53 - 1. 73 (0) 1 x (k) 481. 8 523. 92 535. 90 548. 15 560. 69 573. 51 586. 62 600. 03 613. 76 627. 79 642. 14 相对误差 ( ) 0 - 2. 87 - 0. 56 - 0. 67 - 1. 17 0. 55 4. 97 2. 94 1. 56 - 2. 13 - 3. 41 　　用得到的M GM (1, 2) 模型和两个 GM (1, 1) 模型分别预测两变量 1991、1992 年的值, 并与实际结果进 行比较, 预测结果和相对误差见表 4, 表 5。同样,M GM (1, 2) 模型对两变量均有很好的预测精度, 尤其是一 点预测精度非常高。 而 GM (1, 1) 模型对 x (0) 1 的预测精度很好, 对序列 x (0) 2 的预测精度很差。 由上述结果可见,M GM (1, 2) 模型比较好地反映了国有建筑施工企业就业人数和城镇集体建筑施工 企业就业人数之间的相互制约、共同发展关系。同 GM (1, 1) 模型的对比可以发现, 国有建筑施工企业就业 人数的发展变化具有很大的独立性, 在两变量中起主导作用, 而城镇集体建筑施工企业就业人数的发展变 化要受到前者的很大影响。 4　结束语 从系统的观点,M GM (1, n) 模型是一种状态模型, 它是单变量的 GM (1, 1) 模型在多变量情形下的自 然推广, 旨在反映各变量间相互制约、相互促进的关系。M GM (1, n) 模型不能代替 GM (1, 1) 模型, 而是 GM (1, 1) 模型的扩展和补充。同时,M GM (1, n) 模型不同于 GM (1, n) 模型, 是一种预测模型。将M GM (1, 

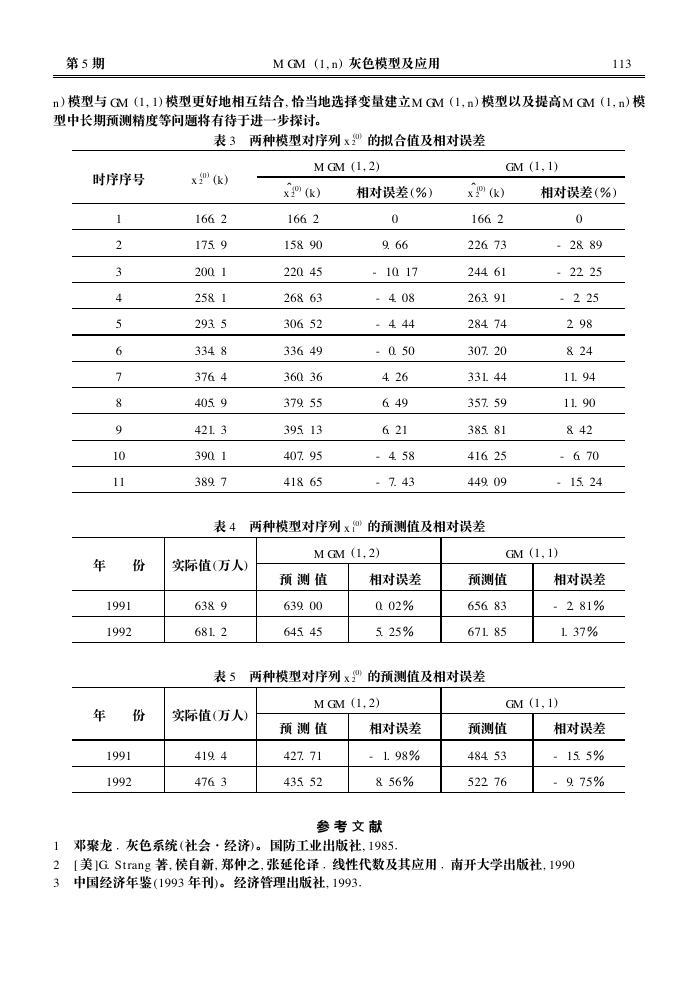
1 1 1 第 5 期 M GM (1, n) 灰色模型及应用 311 n ) 模型与 GM (1, 1) 模型更好地相互结合, 恰当地选择变量建立M GM (1, n) 模型以及提高M GM (1, n) 模 型中长期预测精度等问题将有待于进一步探讨。 表 3　两种模型对序列 x (0) 2 的拟合值及相对误差 时序序号 x (0) 2 (k) 1 2 3 4 5 6 7 8 9 10 11 166. 2 175. 9 200. 1 258. 1 293. 5 334. 8 376. 4 405. 9 421. 3 390. 1 389. 7 M GM (1, 2) GM (1, 1) (0) 2 x (k ) 166. 2 158. 90 220. 45 268. 63 306. 52 336. 49 360. 36 379. 55 395. 13 407. 95 418. 65 相对误差 ( ) 0 9. 66 - 10. 17 - 4. 08 - 4. 44 - 0. 50 4. 26 6. 49 6. 21 - 4. 58 - 7. 43 (0) 2 x (k) 166. 2 226. 73 244. 61 263. 91 284. 74 307. 20 331. 44 357. 59 385. 81 416. 25 449. 09 相对误差 ( ) 0 - 28. 89 - 22. 25 - 2. 25 2. 98 8. 24 11. 94 11. 90 8. 42 - 6. 70 - 15. 24 表 4　两种模型对序列 x (0) 1 的预测值及相对误差 年　　份 实际值 (万人) 预 测 值 相对误差 M GM (1, 2) GM (1, 1) 1991 1992 638. 9 681. 2 639. 00 645. 45 0. 02 5. 25 预测值 656. 83 671. 85 相对误差 - 2. 81 1. 37 表 5　两种模型对序列 x (0) 2 的预测值及相对误差 年　　份 实际值 (万人) 预 测 值 相对误差 M GM (1, 2) GM (1, 1) 1991 1992 419. 4 476. 3 427. 71 435. 52 - 1. 98 8. 56 参 考 文 献 灰色系统 (社会·经济)。 国防工业出版社, 1985 1　邓聚龙 2　[ 美 ]G. Strang 著, 侯自新, 郑仲之, 张延伦译 3　中国经济年鉴 (1993 年刊)。 经济管理出版社, 1993 线性代数及其应用 预测值 484. 53 522. 76 相对误差 - 15. 5 - 9. 75 南开大学出版社, 1990