第1页 / 共6页
第2页 / 共6页
第3页 / 共6页
第4页 / 共6页
第5页 / 共6页
第6页 / 共6页
2014年新疆普通高中会考数学真题及答案.doc
2014 年新疆普通高中会考数学真题及答案
姓名
班级
分数
第Ⅰ卷（选择题，共 48 分）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
一.选择题（共 16 小题，每小题 3 分，共 48 分）
在下列各小题的四个选项中，只有一项是符合题目要求的。
第Ⅰ卷（选择题，共 48 分）
C. {2}
B. {1}
1.设集合 A={0,1}，集合 B={1，2}，则 A∩B 为
A. {0}
D.{0,1，2}
2 函数
f x
B
的定义域为
C.
x x
x x
2
A.R
2
D.
x x
2
3.函数
f x
的奇偶性为
x
2
1
x
B.奇函数
C.非奇非偶函数
A 偶函数
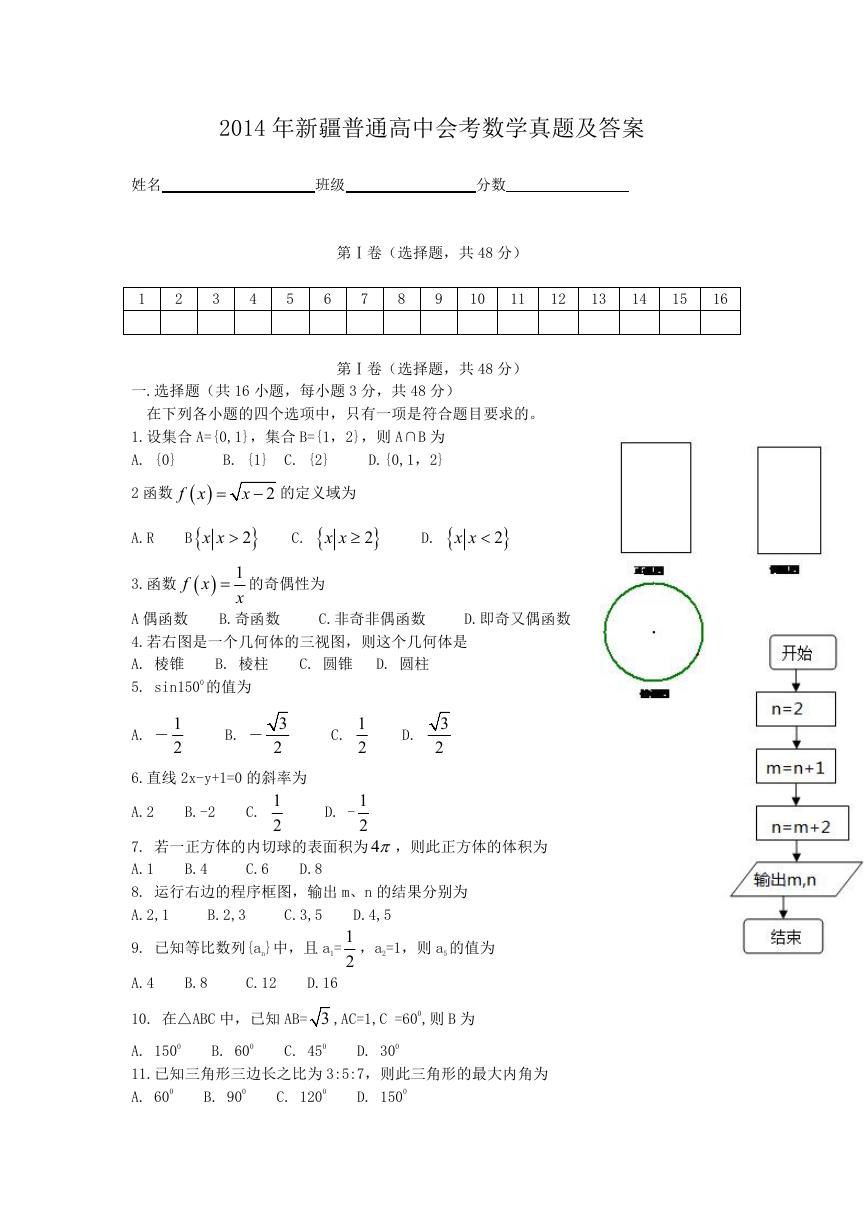
4.若右图是一个几何体的三视图，则这个几何体是
A. 棱锥
5. sin1500 的值为
C. 圆锥 D. 圆柱
B. 棱柱
D.即奇又偶函数
A. ―
1
2
B. ―
3
2
C.
1
2
D.
3
2
6.直线 2x-y+1=0 的斜率为
A.2
B.-2
C.
D. -
1
2
1
2
B.4
7. 若一正方体的内切球的表面积为 4，则此正方体的体积为
A.1
8. 运行右边的程序框图，输出 m、n 的结果分别为
A.2,1
B.2,3
C.3,5
C.6
D.8
9. 已知等比数列{an}中，且 a1=
A.4
B.8
C.12
D.16
D.4,5
1
2
，a2=1，则 a5 的值为
10. 在△ABC 中，已知 AB= 3 ,AC=1,C =600,则 B 为
B. 600
A. 1500
11.已知三角形三边长之比为 3:5:7，则此三角形的最大内角为
A. 600
C. 1200
D. 1500
C. 450
B. 900
D. 300
12．函数 sin(2
y
x
的最小正周期为
)
4
A.
2
B.
C.
3
2
D. 2
13.已知 2
m
n ，则 m、n 的大小关系为
2
A.m>n
B.m n
C.m
22. 已知平面向量 a=（1，-2）b=（-2,1）。求：a•b 及 a b 。
23. 已知等差数列{an}中，公差 d=2，a2=3，求：
（1）a3、a5 的值；
（2）该数列的前 5 项和 S5。
P
24. 如图，在四棱锥
M、N 分别是 PA、PB 的中点，求证：
（1）证明：MN //平面 ABCD；
ABCD
中，底面 ABCD 是矩形， PA 平面 ABCD ，
（2）证明：CD⊥平面 PAD.
25．对甲、乙两名自行车赛手在相同条件下进行了 6 次测试，测得他们最大速度（m/s）的
数据如下表：
甲
乙
27
33
38
29
30
38
37
34
35
28
31
36
（1）用茎叶图表示上面样本的数据；
（2）分别求出甲、乙两名赛手最大速度（m/s）数据的的平均数、方差，并判断谁参加比
赛更合适。
26.已知圆 M 过点 A(1，-1)、B(-1，1)两点，且圆心 M 在直线 x+y-2=0 上
（1）求圆 M 的方程；
（2）若点 P 为直线 3x+4y+8=0 上的动点，PC、PD 分别是圆 M 的两条切线，C、D 为圆 M 的
切点，求四边形 PCMD 面积的最小值。
2013 年新疆普通高中会考参考答案和评分标准
第Ⅰ卷（选择题，共 48 分）
一. 选择题（共 16 小题，每小题 3 分，共 48 分）
1
B
2
C
3
B
4
D
5
C
6
A
7
D
8
C
9
B
10
11
12
13
14
15
16
D
C
B
A
A
D
C
题
号
答
案
二.填空题（本大题共 4 小题，每小题 4 分，共 16 分）
第Ⅱ卷（非选择题，共 52 分）
17．0
18.
4
19. x+y-3=0
20.
24
7
三.解答题（本大题共 6 小题，每小题 6 分，共 36 分）
21.证明：
x
设 、 是区间 ， 上的任意两个实数，且
1
0 +
x
1
x
2
，则
x
2
f x
1
f x
2
1
x
1
x
1
=2+
x
2
2
0,
x
1
1
x
2
x x
1 2
x
2
x x
1 2
0
f x
在区间 ， 是减函数
0
0 +
f x
1
即
2
f x
2
x
1
x
1
0
0
x
2
x
2
x x
1 2
f x
1
f x
1
a b
（-2）
( 1, 1)
a b
2
( 1)
a b
22.解：
( 2) 1
4
( 1)
2
2
23.解：
a
1
1
2
(1)
a
3
a
a
5
(2)
a
a
1
a
1
a
n
3 2 5
d
2
, 3
2,
a
d
即
1
1 8 9
4
d
为等差数列
5 (
)
a
5
S
5
a
1
2
5 (1 9)
2
25
24.证明：（1）∵M、N 分别是 PA、PB 的中点
∴MN∥AB
又∵MN 平面 ABCD
∴MN∥平面 ABCD
（2）∵ PA 平面 ABCD ∴PA⊥CD
∵四边形 ABCD 是矩形 ∴CD⊥AD
∴CD⊥平面 PAD。
25.解（1）
（2）X （27
甲
+38+30+37+35+31 =33
）
X （29
乙
+28+33+38+34+36 =33
）
1=
6
1=
6
S
2
甲
1=
6
S
2
乙
1=
6
2
（31-33）
2
（36-33）
47
3
38
3
2
（27-33） （38-33） （30-33） （37-33） （35-33）
2
2
2
2
2
（29-33） （28-33） （33-33） （38-33） （34-33）
2
2
2
2
S
2
甲
2S 乙 选乙参加比赛更合适。
26.解：
（1）设圆心M(a,-a+2),
2
则（a-1） （-a+3） （a+1） （-a+1）
2
2
2
=
a
1
解得
(2)
2
2
圆心M为（2,1），r （a-1） （-a+3）
2
4
M
圆 的方程为（x-1） （y+3）
2
PC
S
PC CM
2
2
S
2
4
2
PM
8 0
4
上的动点
2
2
PCM
PCMD
2
2
PM r
3
4
x
P
y
点 为直线
3 4+8
PM
min
=3
5
S
PCMD
即四边形
2
2 3
PCMD
2 5
4
的面积最小值为 。
2 5
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
