论文研究-基于时空优化深度神经网络的AQI等级预测.pdf

发布时间：2022-05-29 发布人：admin 分类：说明书资料大小：0.71M 资料格式：pdf 举报版权申诉

weixin_38743737-11698766-4744302542863898366.pdf-第1页.png

第1页 / 共7页

weixin_38743737-11698766-4744302542863898366.pdf-第2页.png

第2页 / 共7页

weixin_38743737-11698766-4744302542863898366.pdf-第3页.png

第3页 / 共7页

weixin_38743737-11698766-4744302542863898366.pdf-第4页.png

第4页 / 共7页

weixin_38743737-11698766-4744302542863898366.pdf-第5页.png

第5页 / 共7页

weixin_38743737-11698766-4744302542863898366.pdf-第6页.png

第6页 / 共7页

weixin_38743737-11698766-4744302542863898366.pdf-第7页.png

第7页 / 共7页

文本预览

Computer Engineering and Applications 计算机工程与应用 2017，53（21） 17 基于时空优化深度神经网络的 AQI 等级预测董婷 1，赵俭辉 1，胡勇 2 DONG Ting1, ZHAO Jianhui1, HU Yong2 1. 武汉大学计算机学院，软件工程国家重点实验室，武汉 430072 2. 武汉大学资源与环境科学学院，武汉 430079 1.State Key Laboratory of Software Engineering, School of Computer Science, Wuhan University, Wuhan 430072, China 2.School of Resources and Environmental Sciences, Wuhan University, Wuhan 430079, China DONG Ting, ZHAO Jianhui, HU Yong. AQI levels prediction based on deep neural network with spatial and temporal optimizations. Computer Engineering and Applications, 2017, 53（21）：17-23. Abstract: The existing air quality prediction models have lower precision, and sensitive to noisy data. Thus a new method is proposed for AQI levels prediction based on Stacked Denoising Auto-Encoders（SDAE）model. Firstly, the historical air quality and meteorological monitoring data of Wuhan city are taken as research object. SDAE model is established to study the characteristic expression of the original data layer by layer, and the last layer is connected with a classifier to tune the prediction model. The optimal set of hyper-parameters is found through improved grid search algorithm for multi- parameters. Then, the prediction is obtained from the test set. The indicators such as mean absolute error and mean square error between the predicted value and related actual value are used as the evaluation standards for forecasting perfor- mance. Compared with other network models, it can be proved that SDAE model has better predictive performance. Finally, the input data is optimized considering their spatial and temporal relations. Experimental results show that the spatial optimization based SDAE has the most improvement for predictive performance, and it can obtain more accurate predictions compared with the traditional methods. Key words: AQI levels; prediction; Stacked Denoising Auto-Encoder（SDAE）; optimization 摘要：针对现有空气质量预测方法精度偏低、对噪声敏感等问题，提出一种基于堆栈降噪自编码（Stacked Denoising Auto-Encoders，SDAE）模型的空气质量等级预测方法。首先以武汉市历史空气质量和气象监测数据为研究对象，建立 SDAE 模型逐层学习原始数据的特征表达，并将最后一层特征与分类器连接完成预测模型的调优。同时改进多参数网格搜索法，选取了最优的超参数组合。然后在测试集上进行预测，并用预测值与实际值之间的平均绝对误差和均方误差等指标作为预测性能评价标准。通过与其他网络模型的实验对比，证明了 SDAE 模型对于空气质量等级具有较优的预测性能。最后从时间、空间、时空三个角度对该模型输入进行优化，实验结果表明基于空间优化的 SDAE 模型预测性能提升最为明显，能够得到比传统方法更加精确的预测结果。关键词：AQI 等级；预测；堆栈降噪自编码；优化文献标志码：A 中图分类号：TP391 doi：10.3778/j.issn.1002-8331.1705-0420 1 引言近几年雾霾天气频发，如果长时间在高浓度污染物环境下活动，容易对人体健康造成直接危害[1-2]，对空气质量等级准确地预测不仅可以帮助公众提前了解未来空气质量情况并合理安排户外活动，还可以在预测到重污染等级天气后通知环保局等有关部门采取措施，预防基金项目：中国空间技术研究院创新基金（No.CAST2014）；湖北省科技支撑计划（No.2014BAA149）；中央高校基本科研业务费专项（No.2042016gf0023）。作者简介：董婷（1992—），女，硕士研究生，研究领域为深度学习及应用、图像处理，E-mail：dongtingwhu@163.com；赵俭辉（1975—），男，博士，副教授，研究领域为人工智能、图形图像；胡勇（1973—），男，博士，副教授，研究领域为空间模型与模拟、气候变化适应与减缓。收稿日期：2017-05-31 修回日期：2017-09-19 文章编号：1002-8331（2017）21-0017-07 计算机工程与应用www.ceaj.org

18 2017，53（21） Computer Engineering and Applications 计算机工程与应用或减缓危害事件的发生。空气质量指数（Air Quality Index，AQI）是一种用来评测空气状况的指标，参与空气质量评价的主要污染物有细颗粒物（PM2.5）、可吸入颗粒物（PM10）、二氧化硫（SO2）、二氧化氮（NO2）、臭氧（O3）、一氧化碳（CO）六项。空气质量按照 AQI 大小分为六级：一级（0~50）优、二级（51~100）良、三级（101~150）轻度污染、四级（151~200）中度污染、五级（201~300）重度污染，六级（>300）严重污染。指数越大、级别越高说明空气污染情况越严重，对人体健康的危害也越大。AQI 与气象条件有极大关系[3]。不同气象状况下污染物扩散条件不同，排入相同数量的污染物，空气中的污染物浓度也会有不同。比如静稳天气条件下风力微弱，容易出现逆温层，不利于颗粒物的扩散，重污染天气易发。而对于风力大、对流强的地区和时段，大气扩散稀释能力强，此时空气质量相对污染物排放量不会像静稳天气下那么敏感。所以，对空气质量等级进行预测需要结合气象条件。对于空气污染物的预测问题，国内外大多采用传统的数值预报和回归统计模型[4-5]。数值预报模型的准确率很大程度依赖于污染源的排放数据，该类数据获取的复杂性和不确定性使得数值预报在实际应用中受到限制。回归统计模型需要通过大量分析建立影响因子与污染物浓度之间复杂的线性或非线性关系，由于难以用确定的数学模型描述这种关系，建模难度较大。近年来，基于神经网络技术的空气污染物预测研究发展迅速，研究表明，人工神经网络比传统的回归模型性能更好。Azid[6]等将主成分分析和神经网络相结合建立了马来西亚空气污染指数 API 的预测模型。Mishra[7]等分别采用多元线性回归分析和人工神经网络对印度新德里的 PM2.5 浓度进行预测，实验证明神经网络的预测结果更好。神经网络具有很强的非线性拟合能力，能够映射复杂的非线性关系，但随着神经网络层数的增加，梯度下降算法可能会收敛到局部极小值，带来的误差会导致结果比浅层网络更差，同时神经网络还有过拟合、泛化能力差、收敛速度慢等缺点[8]。近几年快速发展起来的深度学习理论，已经在计算机视觉、语音识别、自然语言处理等领域得到广泛应用[9-11]。深度学习通过组合低层特征形成更加抽象的高层表示，以发现数据的分布式特征表示[12-13]。利用深度学习，可以对大量的空气质量和气象历史数据进行智能分析和归纳总结，通过解读复杂非结构性数据，挖掘出空气质量指数与各污染物因子以及温度、湿度、风速等气象条件之间的内在关系，并建立起 AQI 与各影响因子之间的复杂计算模型，从而训练一个有效的深度学习模型来对空气质量进行预测。尹文君[14]等基于限制玻尔兹曼机建立深度信念网络对空气质量分因子进行预测，验证了 DBN 对空气污染预报的有效性。截止目前，深度学习在空气质量预测领域的应用仍然较少。由于空气质量或气象监测数据存在噪声，本文提出用堆栈降噪自编码器建立深度学习网络模型 SDAE。 SDAE 最大特点是具有降噪功能，即以一定概率分布随机擦除原始输入数据，使得数据产生破损，在一定程度上减轻了训练数据与测试数据的差异性，可以提取并编码出更具有鲁棒性的特征，实现对空气质量等级更加准确的预测。 2 堆栈降噪自编码预测模型 2.1 SDAE 模型结构自编码器（AE）通过捕捉可以代表输入数据的最重要特征，使输出尽量复现输入信号，AE 包含编码和解码两个过程：其中“编码”是指提取输入数据的特征，而“解码”是为了验证提取的特征是否可以很好表示输入数据。AE 训练过程的最终目标是最小化重构误差，实质上就是缩小输入数据 X 与其特征表达之间的差别。 AE 有一个很大的局限性，因为输入等于输出，所以该模型很可能会学习到没有编码功能的恒等映射。降噪自编码器（DAE）是在 AE 的基础上给输入数据加入噪声，也就是以一定的概率分布随机擦除输入层的某些节点。此时编码器会自动学习去除噪声，从而获得没有被噪声污染的输入信号。训练好后的降噪编码器可以从含噪声的输入中提取到更具鲁棒性的特征，提升了自编码神经网络模型对输入数据的泛化能力。DAE 跟 AE 的区别如图 1 所示。随机擦除降噪自编码传统自编码加入噪声数据 X ′ 隐含层表达 Y 原始输入 X 重构数据 Z L(X,Z) 图 1 传统自编码器与降噪自编码器的区别堆栈降噪自编码模型（SDAE）是将多个去除输出层的 DAE 堆叠到一起构成的深度学习网络模型，把上一个 DAE 隐含层的输出作为下一个 DAE 的输入，通过逐层提取特征，从而得到更抽象的数据特征。当每一层都完成训练后，将最后一个隐含层的输出作为顶层有监督层的输入，用有监督的反向传播算法对整个网络进行微调，使得学习到的特征更优。当整个网络特征学习过程计算机工程与应用www.ceaj.org

董婷，赵俭辉，胡勇：基于时空优化深度神经网络的 AQI 等级预测 2017，53（21） 19 结束后，最后一个隐含层输出即为最终代表原始输入的特征。 2.2 基于 SDAE 的空气质量预测模型 2.2.1 模型应用关于预测模型输入，由于某一天的空气质量，除了与前一天的空气状况和气象因子有关，与预测当天的气象条件也有较强的相关性，加之现有气象预报准确率较高，可为空气质量预测提供有效参考。本文建立的 SDAE 模型输入与文献[14]类似，每条数据分为三部分：第一部分为某天的 AQI 值、空气质量等级、各污染物因子大小等当天空气质量数据；第二部分是当天气象数据；第三部分是预报的第二天气象数据。以 2015 年 1 月 1 日为例，输入数据格式如表 1 所示。输出数据为预测的第二天空气质量等级。预测结果与记录的实测数据进行对比，可用于分析预测算法的性能。 AQI 86 质量等级 2 表 1 输入数据格式（a）当天空气质量数据 PM10 119.1 PM2.5 SO2 45.9 40.8 （b）当天气象数据 CO 1.062 NO2 58 O3 68 最高温度平均温度 9 3 平均气压最小气压最低温度－3 最大能见度最高露点－4 平均能见度平均露点－9 最小能见度最低露点－14 最大风速最大湿度 83 最小风速平均湿度 42 风位方向最小湿度最大气压 9 1 037 降水量 1 034 1 031 18 14 6 11 6 94 0 （c）预报的第二天气象数据最高温度平均温度 9 5 最低温度 1 最高露点 0 平均气压最小气压最大能见度平均能见度平均露点－4 最小能见度最低露点－9 最大风速最大湿度 81 最小风速平均湿度 49 风位方向最小湿度最大气压 14 1 032 降水量 1 029 1 027 13 7 5 18 8 90 0 综上所述，本文所建立的 AQI 等级预测模型结构如图 2 所示，该模型的前半部分由多个 DAE 堆叠而成。输入层 Input 和 Hidden Layer1 构成了第一个 DAE，Hidden Layer1 和 Hidden Layer2 构成了第二个 DAE，依次类推。 h( )i 表示第 i 个 DAE 学习到的特征，最后一个隐含层的输出作为下一步操作的输入。由于全国各地出台的空气污染预警方案大多以 AQI 等级作为预警级别的划分依据，因此本文在堆栈降噪自编码网络的最顶层连接一个分类预测器，把学习到的最终特征作为监督算法的输入，以此实现 AQI 等级预测功能。最常用的多分类器是 softmax 和多逻辑回归分类器。本文预测模型中，六个等级之间无重合，所以选用 softmax 分类器。用于训练分类器的样本集是堆栈降噪自编码提取到的特征集，对于代价凸函数，通过迭代算法得到全局最优解之后，就可以得到训练好的 softmax 分类器。 2.2.2 模型训练该预测模型的训练过程分为两步：（1）无监督逐层预训练。每层作为一个 DAE 模型进行训练，目的是最小化上层输出在该层的重构误差。每次训练一层，只有当第 i 层训练完成后，才可以训练第 i + 1 层。（2）有监督微调。当每一层都完成训练后，将最后一个隐含层的输出作为顶层有监督层的输入，有监督的训练 softmax 分类器，并使用反向传播算法对整个网络进行微调，使得学习到的特征更优。 3 预测模型设置 3.1 预测性能指标本实验测试数据中，有接近一半的空气质量为 2 级，通过对全国各地空气质量等级历史数据的分布统计，这与现实情况是相符的。对于这样的测试集，即使不训练学习模型而直接把每一天空气质量都预测为 2 级，也能得到 47%的准确率，因此仅用准确率来判断预测模型的性能好坏显然是不合适的。本文在训练模型时，采用平均绝对误差（Mean Absolute Error，MAE）和均方误差（Mean Squared Error，MSE）作为预测精度的评估标准，其中平均绝对误差的计算公式如下： h(n - 1) 1 h(n - 1) 2 h(n - 1) 3 …… x1 x2 … xm +1 input h(1) 1 h(1) 2 h(1) 3 … h(1) n - 1 h(1) n +1 h(2) 1 h(2) 2 h(2) 3 … h(2) n - 1 h(2) n +1 h(n - 1) n - 1 h(n - 1) n +1 Hidden Layer n-1 SDAE 预测模型 Hidden Layer 1 Hidden Layer 2 图 2 h(n) 1 h(n) 2 h(n) 3 … h(n) n - 1 h(n) n Hidden Layer n S o f t m a x 分类器计算机工程与应用www.ceaj.org

20 2017，53（21） Computer Engineering and Applications 计算机工程与应用 MAE = 1 n∑ n |xi - xi'| i = 1 均方误差的计算公式如下： MSE = 1 ) xi - xi' 2 n∑ n ( i = 1 （1）（2）以上两个公式中，n 为数据长度，也就是测试集的天数，xi 为第 i 天空气污染指数等级真实值，xi' 为第 i 天空气污染指数等级的预测值。 3.2 超参数选取深度神经网络中，选取合适的超参数是比较困难但又极其重要的一步，这直接影响到神经网络模型的性能，但是目前理论上还没有一种科学的和普遍的超参数确定方法。以往研究[15-16]对于深度网络超参数的选取基本都带有经验性、偶然性，对于网络结构的确定通常会作为一个独立的环节，而未考虑其他超参数的影响。但是深度神经网络中网络层数、隐含层节点数、学习率、训练迭代次数等参数之间具有相关性，且大多时候没有明显规律。为了避免参数选择的盲目性和随意性，本文改进多参数网格搜索法进行参数选取。该方法先对每个参数选取典型区间、典型步长的值，将超参数组合所在的空间维度划分为合适的网格，然后遍历网格中的每一个点并比较择优，初步得到若干个较优的网格点。该方法的第二步是在找到的较优超参数网格点附近，进行基于更细网格的二次遍历，得到若干更优的参数组合，再通过比较选取最优的一组。这种参数选取方法在很大程度上避免了局部最优问题，可以保证选取的参数组合比较理想，从而避免较大误差。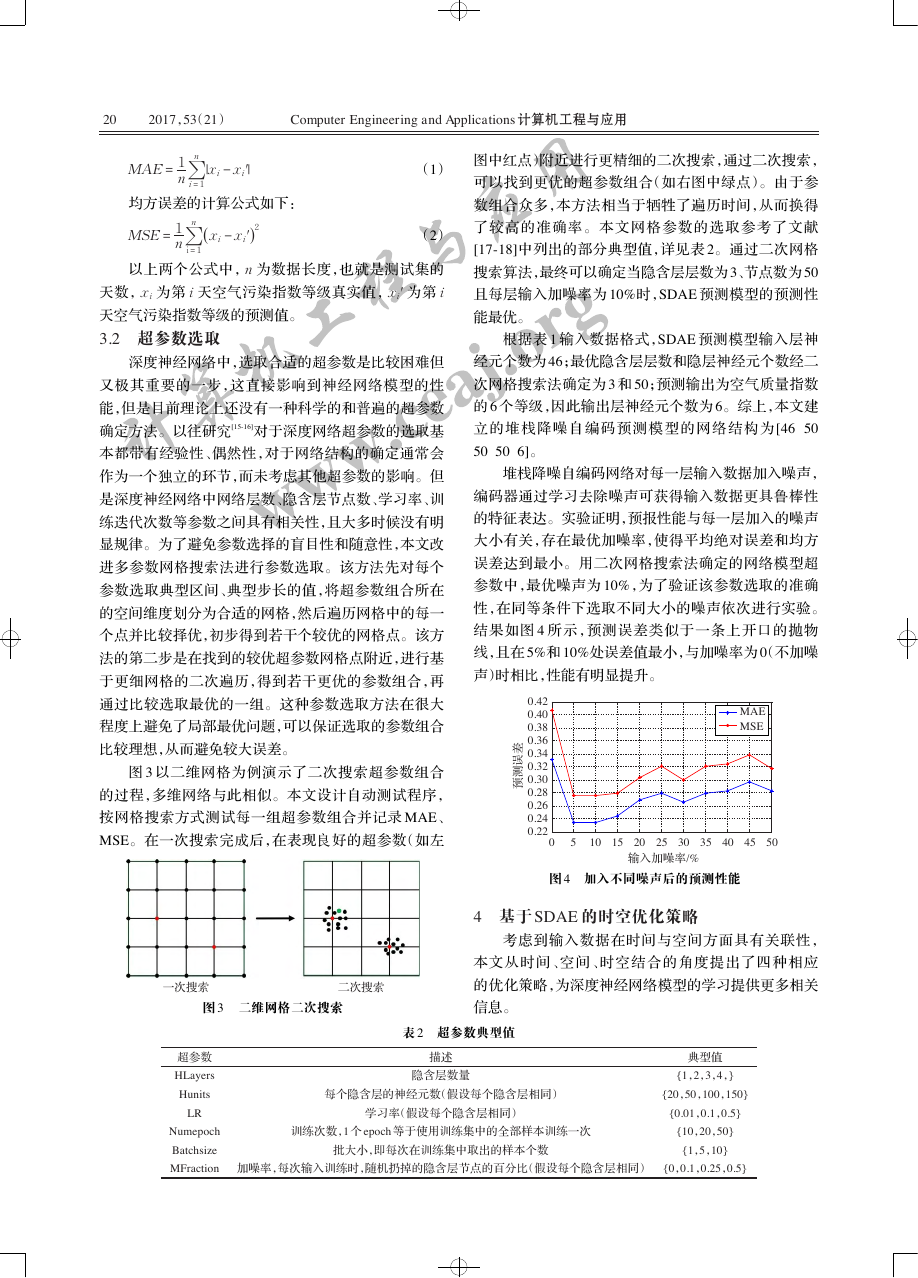图 3 以二维网格为例演示了二次搜索超参数组合的过程，多维网络与此相似。本文设计自动测试程序，按网格搜索方式测试每一组超参数组合并记录 MAE、 MSE。在一次搜索完成后，在表现良好的超参数（如左图中红点）附近进行更精细的二次搜索，通过二次搜索，可以找到更优的超参数组合（如右图中绿点）。由于参数组合众多，本方法相当于牺牲了遍历时间，从而换得了较高的准确率。本文网格参数的选取参考了文献 [17-18]中列出的部分典型值，详见表 2。通过二次网格搜索算法，最终可以确定当隐含层层数为 3、节点数为 50 且每层输入加噪率为 10%时，SDAE 预测模型的预测性能最优。根据表 1 输入数据格式，SDAE 预测模型输入层神经元个数为 46；最优隐含层层数和隐层神经元个数经二次网格搜索法确定为 3 和 50；预测输出为空气质量指数的 6 个等级，因此输出层神经元个数为 6。综上，本文建立的堆栈降噪自编码预测模型的网络结构为[46 50 50 50 6]。堆栈降噪自编码网络对每一层输入数据加入噪声，编码器通过学习去除噪声可获得输入数据更具鲁棒性的特征表达。实验证明，预报性能与每一层加入的噪声大小有关，存在最优加噪率，使得平均绝对误差和均方误差达到最小。用二次网格搜索法确定的网络模型超参数中，最优噪声为 10%，为了验证该参数选取的准确性，在同等条件下选取不同大小的噪声依次进行实验。结果如图 4 所示，预测误差类似于一条上开口的抛物线，且在 5%和 10%处误差值最小，与加噪率为 0（不加噪声）时相比，性能有明显提升。 0.42 0.40 0.38 0.36 0.34 0.32 0.30 0.28 0.26 0.24 0.22 差误测预 MAE MSE 0 5 10 15 20 25 30 35 40 45 50 输入加噪率/% 图 4 加入不同噪声后的预测性能一次搜索二次搜索图 3 二维网格二次搜索 4 基于 SDAE 的时空优化策略考虑到输入数据在时间与空间方面具有关联性，本文从时间、空间、时空结合的角度提出了四种相应的优化策略，为深度神经网络模型的学习提供更多相关信息。表 2 超参数典型值描述隐含层数量每个隐含层的神经元数（假设每个隐含层相同）学习率（假设每个隐含层相同）训练次数，1 个 epoch 等于使用训练集中的全部样本训练一次批大小，即每次在训练集中取出的样本个数典型值 {1，2，3，4，} {20，50，100，150} {0.01，0.1，0.5} {10，20，50} {1，5，10} 加噪率，每次输入训练时，随机扔掉的隐含层节点的百分比（假设每个隐含层相同） {0，0.1，0.25，0.5} 超参数 HLayers Hunits LR Numepoch Batchsize MFraction 计算机工程与应用www.ceaj.org 051015202530354045500.220.240.260.280.30.320.340.360.380.40.42输入加噪率(%)预测误差

董婷，赵俭辉，胡勇：基于时空优化深度神经网络的 AQI 等级预测 2017，53（21） 21 时间优化（Temporal Optimization，TO）：当前时刻的空气质量会受到过去一段时间的影响，在污染物扩散条件差的情况下，时间影响范围相应变大。从模式识别角度来讲，增大时间粒度有可能发现和提取出更多有用的特征。为了确定合适大小的时间粒度，在基于前一天数据建立的 SDAE 预测模型基础上，又分别建立时间属性为 2 天和 3 天的模型，并为每种模型选取二次网格搜索结果中预测误差最小的前 30 组进行统计。实验结果如图 5 所示，时间粒度为 2 天的模型，不论最优 MAE、MSE 还是平均 MAE、MSE，预测误差均比时间粒度为 1 天和 3 天的模型小，因此以 2 天为时间划分基数对模型输入数据进行优化调整，建立 TO-SDAE 时间优化模型。 0.30 0.28 0.26 0.24 差误测预 0.22 前 1 天 MAE MSE MMAE MMSE 前 2 天时间粒度/天前 3 天图 5 不同时间粒度下的时间优化模型性能空间优化（Spatial Optimization，SO）：受气象条件影响，空气污染因子具有扩散性，目标城市的空气质量会受到周边区域影响。因此基于单个城市的空气质量预测存在一定局限性，需要对 SDAE 模型进行空间上的优化。以武汉为中心点，对周边城市按直线距离进行排序，由近至远依次为南昌、长沙、合肥、郑州等（由于数据来源限制，本文只考虑省会城市），并针对武汉及周边最近的 1、2、3、4 个城市的数据分别建立不同空间粒度下的优化模型，为每种模型选取二次网格搜索结果中预测误差最小的前 30 组进行统计。实验结果如图 6 所示，可以看出，空间粒度为 3 天的模型预测误差各指标均为最小，因此以周边 3 城市为空间粒度对模型输入数据进行优化调整，建立 SO-SDAE 空间优化模型，此时模型输入除了武汉自身数据外，还包括长沙、南昌、合肥三个城市的相关数据。 0.30 0.28 0.26 0.24 0.22 0.20 差误测预 MAE MSE MMAE MMSE 1 2 3 4 空间粒度（周边城市数）图 6 不同空间粒度下的空间优化模型性能全局时空优化（Global Spatio-Temporal Optimiza- tion，GSTO）：前文针对时间优化模型，确定了基于前 2 天数据的最佳时间优化粒度；针对空间优化模型，确定了基于周边 3 城市数据的最佳空间优化粒度。基于这两种优化策略的启发，从时空结合的角度对模型进行优化。即预测武汉市第 i + 1 天的空气质量等级时，输入数据包括武汉、长沙、南昌、合肥四个城市前两天的空气质量和气象因子历史数据，以及预测当天的气象预报数值。基于这种优化策略，建立 GSTO-SDAE 时空优化模型。局部时空优化（LocalSpatio-Temporal Optimization， LSTO）：针对全局时空优化过程中可能引入的关联度较低数据，提出一种局部时空优化策略，即选取时间和空间上的关键信息，排除关联度低的输入信息对模型造成的干扰，建立 LSTO-SDAE 局部时空优化模型。具体而言，输入数据包括武汉市第 i - 1 天的空气质量和气象因子数据（不包括周边 3 城市第 i - 1 天的信息），武汉、长沙、南昌、合肥四个城市第 i 天的空气质量和气象因子数据，以及预测当天的气象预报数据。图 7 展示了 GSTO-SDAE 和 LSTO-SDAE 两种时空优化模型的输入区别。LSTO-SDAE 认为周边城市时间较远的数据对于预测武汉市空气质量的影响不大，因此不予考虑。第 i - 1 天第 i 天第 i + 1 天 GSTO LSTO 武汉长沙南昌合肥图 7 全局与局部时空优化模型输入数据区别 5 实验与结果分析 5.1 实验数据预处理本文对武汉市 2013 年 12 月至 2016 年 9 月日均空气质量相关数据和气象数据即污染物扩散条件信息进行收集，选择 2013 年 12 月至 2015 年 11 月的 730 条数据作为深度神经网络的训练数据，剩余的 290 条数据作为测试数据。影响空气质量的因子众多，且每个因子具有各自的物理性质和量纲，如果直接拿这些数据进行分析，会影响结果的准确性。为便于网络训练，防止计算过程出现 “过拟合”等问题，需先对原始数据进行归一化处理，让不同影响因子处于同一数量级，以便进行更精确的数据分析。本文采用 Min-Max 标准化方法，也就是对原始数据的各属性进行一种线性变换，经过标准化之后的数据处于[0，1]之间，标准化函数如下：计算机工程与应用www.ceaj.org前2天前3天0.220.240.260.28时间粒度(天)预测误差 12340.20.220.240.260.28预测误差

22 2017，53（21） Computer Engineering and Applications 计算机工程与应用 x' = x - min max - min （3）其中 x 是归一化之前的数据，x' 是归一化之后的数据， min 是 x 所属影响因子中所有数据的最小值，max 是 x 所属影响因子中所有数据的最大值。对训练集做归一化后，相应的也要对测试数据进行同样的标准化，从而保证测试数据与训练集同比例缩放。但是大多数空气质量和气象数据的值没有确切边界，对于个别小于训练集最小值或大于最大值的测试数据，为了其归一化能落在[0，1]区间内，在上式基础上增加如下限制： 0, x < min x' = ì í 1, x > max î （4） 5.2 不同网络模型预测性能对比为了验证基于堆栈降噪自编码网络模型的预测效果，将优化前的 SDAE 模型与传统神经网络（Neural Network，NN）、深度信念网络（Deep Belief Network， DBN）以及堆栈自编码网络（Stacked Auto- Encoders， SAE）相比。在对比实验中，对所有网络模型结构超参数的确定，统一采用上文提出的二次网格搜索法，得到最优参数组合。为了使对比实验更合理，消除仅对比最优预测结果可能导致的偶然性，本文对各网络模型分别选取了二次网格搜索结果中预测误差最小的前 30 组，对比其总体性能分布。平均绝对误差和均方误差箱形图如图 8、9 所示，SDAE 的最优预测性能、平均预测性能和模型稳定性均明显优于其他几种网络。 E A M E S M 0.32 0.31 0.30 0.29 0.28 0.27 0.26 0.25 0.24 0.23 NN SDAE 图 8 四种网络模型平均绝对误差对比 DBN SAE 0.40 0.38 0.36 0.34 0.32 0.30 0.28 0.26 NN DBN SAE SDAE 图 9 四种网络模型均方误差对比 5.3 不同优化策略下 SDAE 模型性能对比针对本文提出的四种空气质量预测时空优化策略，分别建立对应的预测模型。与之前实验类似，为了实验结果的可靠性，每种优化模型选取二维网格搜索结果中预测误差最小的前 30 组，并与优化之前的 SDAE 相比，得到如下箱形图。从左至右分别是优化前的 SDAE 模型、基于时间优化策略的 TO-SDAE 模型、基于空间优化策略的 SO-SDAE 模型、基于全局时空优化策略的 GSTO- SDAE 模型和基于局部时空优化策略的 LSTO-SDAE 模型，五种网络输入层节点分别为 46、73、184、292、211。基于图 10 和图 11 的实验对比，发现以下结果。 E A M E S M 0.27 0.26 0.25 0.24 0.23 0.22 0.21 0.20 SDAE LSTO 图 10 四种优化策略平均绝对误差对比 GSTO TO SO 0.34 0.32 0.30 0.28 0.26 0.24 0.22 SDAE TO SO GSTO LSTO 图 11 四种优化策略均方误差对比本文提出的四种优化策略中，时间优化、空间优化和局部时空优化这三种模型均比优化前的 SDAE 模型预测性能更优。其中基于空间优化的模型性能提升最大，局部时空优化次之，时间优化性能提升较小。分析原因，由于本文实验数据为日均数据，以天为单位进行空气质量预测时，AQI 在时间上的关联性较差，不如空间关联性紧密，因此基于空间优化策略的性能提升更加明显。基于全局时空优化的模型性能较差，原因是在输入数据中引入了关联度较低的数据，对模型提取输入特征造成了干扰，致使预测性能下降。基于局部时空优化的模型性能好于全局时空优化，但仍低于空间优化，原因仍在于以天为单位数据的时间关联性较差，从而影响了局部时空优化的性能。 5.4 优化模型与其他预测方法的对比采用基于空间优化策略的 SO-SDAE 模型作为预测模型，在测试数据集上进行验证，并对所有预测值和实际值的差值进行统计，结果如图 12 所示。在 290 天的测试数据中，有 233 天的空气质量等级能被准确预测，54 天会被错误预测为相邻等级，只有 3 天的预测误差为 2 个等级，没有 3 级及以上误差，总体预测性能较优。文献[19]分别用当前常用的空气预测方法：综合指标法（Comprehensive Index Method，CIM）和逐步回归计算机工程与应用www.ceaj.org图8 四种网络模型平均绝对误差对比图9 四种网络模型均方误差对比图10 四种优化策略平均绝对误差对比 NNDBNSAESDAE0.230.240.250.260.270.280.290.30.310.32MAENNDBNSAESDAE0.260.280.30.320.340.360.380.4MSESDAETOSOGSTOLSTO0.20.210.220.230.240.250.260.27MAESDAETOSOGSTOLSTO0.220.240.260.280.30.320.34MSE图8 四种网络模型平均绝对误差对比图9 四种网络模型均方误差对比图10 四种优化策略平均绝对误差对比 NNDBNSAESDAE0.230.240.250.260.270.280.290.30.310.32MAENNDBNSAESDAE0.260.280.30.320.340.360.380.4MSESDAETOSOGSTOLSTO0.20.210.220.230.240.250.260.27MAESDAETOSOGSTOLSTO0.220.240.260.280.30.320.34MSE图8 四种网络模型平均绝对误差对比图9 四种网络模型均方误差对比图10 四种优化策略平均绝对误差对比 NNDBNSAESDAE0.230.240.250.260.270.280.290.30.310.32MAENNDBNSAESDAE0.260.280.30.320.340.360.380.4MSESDAETOSOGSTOLSTO0.20.210.220.230.240.250.260.27MAESDAETOSOGSTOLSTO0.220.240.260.280.30.320.34MSE图8 四种网络模型平均绝对误差对比图9 四种网络模型均方误差对比图10 四种优化策略平均绝对误差对比 NNDBNSAESDAE0.230.240.250.260.270.280.290.30.310.32MAENNDBNSAESDAE0.260.280.30.320.340.360.380.4MSESDAETOSOGSTOLSTO0.20.210.220.230.240.250.260.27MAESDAETOSOGSTOLSTO0.220.240.260.280.30.320.34MSE

董婷，赵俭辉，胡勇：基于时空优化深度神经网络的 AQI 等级预测 2017，53（21） 23 ）级等（差之值际实与值测预 2 1 0 －1 －2 Dec Jan Feb Mar Apr May Jun Jul Aug Sep 时间/天图 12 预测值与实际值的误差统计法（Stepwise Regression Method，SRM）建立了 AQI 等级预报统计模型。其中 CIM 采用了拟合率作为预测性能评价指标，即将 AQI 等级 1~2 级认定为空气质量好， 3~6 级为空气质量差，正确预测到第二天空气状况（好与差）的天数占总天数的比例。SRM 采用了各误差级数占比作为评价指标，即预测级数与真实级数之差的绝对值分别为 0（准确率）、1、2、3 及以上的天数占总天数的比例。本文采用完全一样的评价指标，与文献[19]的方法进行对比，结果如表 3 所示。可见本文提出的基于空间优化的 SO-SDAE 预测模型的拟合率高于 CIM，准确率高于 SRM 模型，其余误差级数所占比例整体低于 SRM 模型。与优化前的 SDAE 模型相比，SO-SDAE 的拟合率和准确率均有较明显的提升，同时误差级数占比减少，尤其是误差为 2 级的天数从 6 天缩减为 3 天，减少一半。表 3 几种预测方法的性能对比模型拟合率准确率误差 1 级率误差 2 级率 CIM SRM SDAE SO-SDAE 76.0 — 92.0 94.8 — 65.0 78.6 80.3 — 32.0 19.4 18.6 — 2 2 1 % 误差 3 级率 — 1 0 0 6 结论本文提出一种基于时空优化的堆栈降噪自编码空气质量预测模型。利用无监督学习算法的优势，自动对有噪声的输入数据逐层提取特征，通过训练学习建立起空气质量等级与污染物因子浓度、气象数据之间的关系模型。采用武汉地区空气质量数据进行实验分析，通过实验对比，得出以下结论：（1）以 MAE、MSE 作为预测性能评价标准，证明了基于 SDAE 的空气质量等级预测模型比 BP、DBN、SAE 三种网络模型的预测性能更优、结果更稳定。（2）基于时间、空间、局部时空三种优化策略的 SDAE 预测模型与优化之前相比，性能均有提升，其中基于空间优化的模型性能最优。从全局时空优化实验结果可以看出，如果输入引入关联度较低的数据，会对模型的特征提取造成干扰，导致预测效果较优化前变差。（3）以拟合率、准确率和不同误差级数占比作为预测性能评价标准，依次与综合指标法和逐步回归法预测模型进行对比，证明了本文提出的基于空间优化的 SDAE 模型预测性能更好。随着今后更多监测数据的积累，可以得到空气质量各等级更充足的数据，从而使深度神经网络模型学习到每个等级更具代表性的特征表达，以此对各级污染天气做出更加精准的预测。此外，如果基于更大量样本的学习，例如以小时为单位的污染物和气象数据，以及省会城市之外的更多城市的监测数据，将会得到精度更高的预测结果，尤其会提升时空模型的性能。参考文献： [1] Kelly F J，Fussell J C.Air pollution and public health： Emerging hazards and improved understanding of risk[J]. Environmental Geochemistry and Health，2015，37（4）： 631-649. [2] Mclaren J，Williams I D.The impact of communicating information about air pollution events on public health[J]. Science of the Total Environment，2015，538：478-491. [3] Gilliam R C，Hogrefe C，Godowitch J M，et al.Impact of inherent meteorology uncertainty on air quality model predictions[J].Journal of Geophysical Research：Atmo- spheres，2016，120（23）：259-280. [4] Pérez V A，Arasa R，Codina B，et al.Enhancing air quality forecasts over Catalonia（Spain）using model output statics[J]. Journal of Geoscience & Environment Protection，2015，3 （8）：9-22. [5] Xu Bin，Luo Liangqing，Lin Boqiang.A dynamic analysis of air pollution emissions in China：evidence from non- parametric additive regression models[J].Ecological Indi- cators，2016，63：346-358. [6] Azid A，Juahir H，Toriman M E，et al.Prediction of the level of air pollution using principal component analysis and artificial neural network techniques：A case study in Malaysia[J].Water，Air，& Soil Pollution，2014，225（8）： 2063. [7] Mishra D，Goyal P，Upadhyay A.Artificial intelligence based approach to forecast PM2.5 during haze episodes： A case study of Delhi，India[J].Atmospheric Environment， 2015，102：239-248. [8] 卢辉斌，李丹丹，孙海艳 .PSO 优化 BP 神经网络的混沌时间序列预测[J]. 计算机工程与应用，2015，51（2）：224-229. [9] 奚雪峰，周国栋 . 面向自然语言处理的深度学习研究[J]. 自动化学报，2016，42（10）：1445-1465. [10] 吴财贵，唐权华 . 基于深度学习的图片敏感文字检测[J]. 计算机工程与应用，2015，51（14）：203-206. （下转 41 页）计算机工程与应用www.ceaj.org图12 预测值与实际值的误差统计 -2-1012时间(天)

分享到：

赞收藏

资料库

论文研究-基于时空优化深度神经网络的AQI等级预测.pdf

相关推荐

开发技术

热门标签

最新资料