2013年重庆市中考数学真题B卷.doc-资料库

第1页 / 共7页

第2页 / 共7页

第3页 / 共7页

第4页 / 共7页

第5页 / 共7页

第6页 / 共7页

第7页 / 共7页

2013 年重庆市中考数学真题 B 卷（本卷共四个大题满分 150 分考试时间 120 分钟）参考公式：抛物线 y  2 ax  bx  ( ac  )0 的顶点坐标为 (  b 2 a 4, ac  4 a 2 b ) ，对称轴公式为 x  b 2 a 一、选择题：（本大题 12 个小题，每小题 4 分，共 48 分） 1、在-2，0，1，-4 这四个数中，最大的数是 A.-4 B.-2 C.0 D.1 2、如图，直线 a、b、c、d,已知 c  , ca  b ，直线 b、c、d 交于一点，若 1  050 ，则 2 等于 B.50° D.30° 33 x  的结果是 x 2 A.60° C.40° 3、计算 A. 22x B. 23x D.3 ∽ DEF  ，若 ABC 与 DEF  的相似比为 3：4，则 ABC 与 DEF  的面积之比为 C. x3 4、已知 ABC A.4：3 B.3：4 C.16：9 D.9：16 5、已知正比例函数 y=kx( 0k )的图象经过点（1，-2），则正比例函数的解析式为 A. y 2 x B. y 2 x C. y 1 2 x D. y 1 2 x 6、为了比较甲乙两种水稻秧苗谁出苗更整齐，每种秧苗各随机抽出 50 株，分别量出每株长度，发现两组秧苗的平均长度一样，甲、乙的方差分别是 3.5、10.9，则下列说法正确的是 A.甲秧苗出苗更整齐 B. 乙秧苗出苗更整齐 C.甲、乙出苗一样整齐 D.无法确定甲、乙出苗谁更整齐 7、如图，矩形纸片 ABCD 中，AB=6cm,BC=8cm,现将其沿 AE 对折，使得点 B 落在边 AD 上的点 1B 处，折痕与边 BC 交于点 E，则 CE 的长为 A.6cm B.4cm C.2cm D.1cm 8、如图，AB 是⊙O 的切线，B 为切点，AO 与⊙O 交于点 C，若 BAO 040 ,则 OCB 的度数为 A.40° B.50° C.65° D.75°

9、如图，在 ABC 中， 045A , 030B , CD  AB ,垂足为 D，CD=1，则 AB 的长为 A.2 B. 32 C. 3  3 1 D. 13  10、2013 年“中国好声音”全国巡演重庆站在奥体中心举行.童童从家出发前往观看，先匀速步行至轻轨车站，等了一会儿，童童搭乘轻轨至奥体中心观看演出，演出结束后，童童搭乘邻居刘叔叔的车顺利到家. 其中 x 表示童童从家出发后所用时间，y 表示童童离家的距离.下图能反映 y 与 x 的函数关系式的大致图象是 11、下列图形都是由同样大小的棋子按一定的规律组成，其中第①个图形有 1 颗棋子，第②个图形一共有 6 颗棋子，第③个图形一共有 16 颗棋子，…，则第⑥个图形中棋子的颗数为 A.51 B.70 C.76 D.81 12、如图，在平面直角坐标系中，正方形 OABC 的顶点 O 与原点重合，顶点 A,C 分别在 x 轴、y 轴上，反比例函数 y  k x ( k  ,0 x  )0 的图象与正方形的两边 AB、BC 分别交于点 M、N, ND  轴x ，垂足为 D，连接 OM、ON、MN. 下列结论： ① OCN   OAM ; ②ON=MN; ③四边形 DAMN 与 MON  面积相等； ④若 MON 045 ,MN=2,则点 C 的坐标为（0， 12  ）. 其中正确结论的个数是（） A.1 B.2 C.3 D.4 填空题：（本大题 6 个小题，每小题 4 分，共 24 分） 13、实数“-3”的倒数是； 14、分式方程 1  2 x 1 的解为；

15、某届青年歌手大奖赛上，七位评委为甲选手打出的分数分别是：96.5，97.1， 97.5，98.1，98.1，98.3，98.5.则组数据的众数是； 16、如图，一个圆心角为 090 的扇形，半径 OA=2，那么图中阴影部分的面积为；（结果保留） 17、在平面直角坐标系中，作 OAB  ，其中三个顶点分别是 O(0,0),B(1,1),A(x,y)( 2-  2-2 x ，  y ,2 x,y 均为整数)，则所作 OAB  为直角三角形的概率是； 18、如图，平面直角坐标系中，已知直线 y=x 上一点 P（1，1），C 为 y 轴上一点，连接 PC，线段 PC 绕点 P 顺时针旋转 90°至线段 PD，过点 D 作直线 AB  轴x ，垂足为 B，直线 AB 与直线 y=x 交于点 A，且 BD=2AD，连接 CD，直线 CD 与直线 y=x 交于点 Q，则点 Q 的坐标为 . 三、解答题：（本大题 2 个小题，每小题 7 分，共 14 分）四、19、计算： 2013 )1(   2  0   3  3  8  1    1 4    20、如图，在边长为 1 的小正方形组成的 10 网格中（我们把组成网格的小正方形的顶点称为格点），四边形 ABCD 在直线l 的左侧， 10 其四个顶点 A、B、C、D 分别在网格的顶点上. (1)请你在所给的网格中画出四边形 ' ' DCBA ' ' ,使四边形 ' ' DCBA ' ' 和四边形 ABCD 关于直线l 对称，其中，点 ' DCBA 、、、 ' ' ' 分别是点 A、B、C、D 的对称点； (2)在（1）的条件下，结合你所画的图形，直接写出线段 ' 'BA 的长度. 四、解答题：（本大题 4 个小题，每小题 10 分，共 40 分） 21、先化简，再求值： 2  x (  x x x   1 2 )  x   4 4 x  4 2 x ，其中 x 是不等式 3 17 x 的负整数解.

22、为了贯彻落实国家关于增强青少年体质的计划，重庆市全面实施了义务教育学段中小学学生“饮用奶计划”的营养工程.某牛奶供应商拟提供 A（原味）、B（草莓味）、C（核桃味）、D（菠萝味）、 E（香橙味）等五种口味的学生奶供学生选择（所有学生奶盒性状、大小相同），为了了解对学生奶口味的喜好情况，某初中学九年级（1）班张老师对全班同学进行了调查统计，制成了如下两幅不完整的统计图：（1）该班五种口味的学生奶喜好人数组成一组统计数据，直接写出这组数据的平均数，并将折线统计图补充完整；（2）在进行调查统计的第二天，张老师为班上每位同学发放一盒学生奶.喜好 B 味的小明和喜好 C 味的小刚等四位同学最后领取，剩余的学生奶放在同一纸箱里，分别有 B 味 2 盒，C 味和 D 味各 1 盒，张老师从该纸箱里随机取出两盒学生奶.请你用列表法或画树状图的方法，求出这两盒牛奶恰好同时是小明和小刚喜好的学生奶的概率. 23、4.20 雅安地震后，某商家为支援灾区人民，计划捐赠帐篷 16800 顶，该商家备有 2 辆大货车、8 辆小车运送，计划大货车比小货车每辆每次多运帐篷 200 顶，大、小货车每天均运送一次，两天恰好运完. （1）求大、小货车原计划每辆每次各运送帐篷多少顶？（2）因地震导致路基受损，实际运送过程中，每辆大货车每次比原计划少运 m200 顶，每辆小货车每次比原计划少运 300 顶.为了尽快将帐篷运送到灾区，大货车每天比原计划多跑 m 1 2 多跑 m 次，一天刚好运送了帐篷 14400 顶，求 m 的值. 次，小货车每天比原计划 24、已知：在平行四边形 ABCD 中， AE  BC ,垂足为 E，CE=CD,点 F 为 CE 的中点，点 G 为 CD 上的一点，连接 DF、EG、AG, 1  2 . （1）若 CF=2,AE=3,求 BE 的长；（2）求证：  CEG  1 2 AGE .

五、解答题：（本大题 2 个小题，每小题 12 分，共 24 分） 25、如图，已知抛物线 y  2 x  bx  c 的图像与 x 轴的一个交点为 B（5,0），另一个交点为 A，且与 y 轴交于点 C(0,5). （1）求直线 BC 与抛物线的解析式；（2）若点 M 是抛物线在 x 轴下方图像上的一动点，过点 M 作 MN//y 轴交直线 BC 于点 N，求 MN 的最大值；（3）在（2）的条件下，MN 取得最大值时，若点 P 是抛物线在 x 轴下方图像上任意一点，以 BC 为边作平行四边形 CBPQ,设平行四边形 CBPQ 的面积为 1S ，△ABN 的面积为 2S ，且 S  1 6S 2 ，求点 P 的坐标.

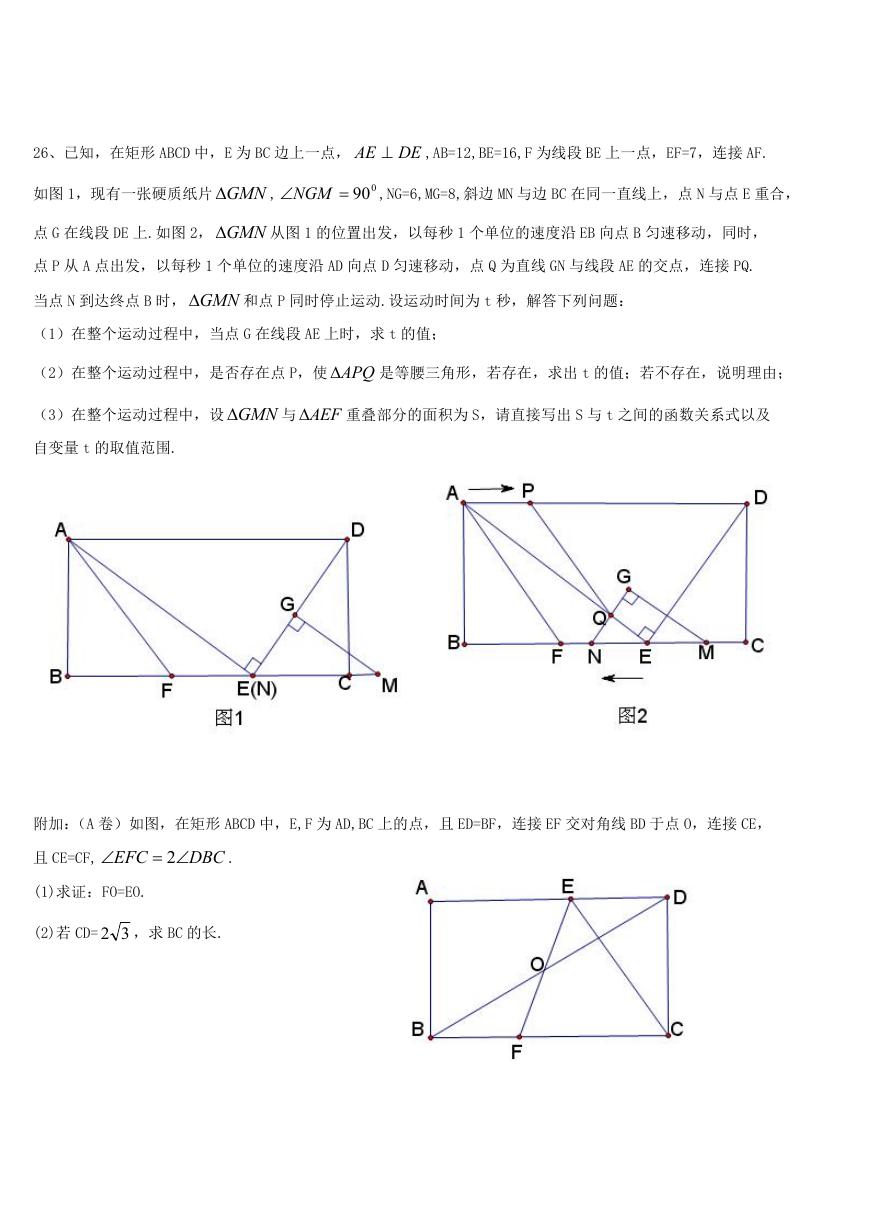
26、已知，在矩形 ABCD 中，E 为 BC 边上一点， AE  DE ,AB=12,BE=16,F 为线段 BE 上一点，EF=7，连接 AF. 如图 1，现有一张硬质纸片 GMN  , NGM 090 ,NG=6,MG=8,斜边 MN 与边 BC 在同一直线上，点 N 与点 E 重合，点 G 在线段 DE 上.如图 2， GMN  从图 1 的位置出发，以每秒 1 个单位的速度沿 EB 向点 B 匀速移动，同时，点 P 从 A 点出发，以每秒 1 个单位的速度沿 AD 向点 D 匀速移动，点 Q 为直线 GN 与线段 AE 的交点，连接 PQ. 当点 N 到达终点 B 时， GMN  和点 P 同时停止运动.设运动时间为 t 秒，解答下列问题：（1）在整个运动过程中，当点 G 在线段 AE 上时，求 t 的值；（2）在整个运动过程中，是否存在点 P，使 APQ 是等腰三角形，若存在，求出 t 的值；若不存在，说明理由；（3）在整个运动过程中，设 GMN  与 AEF 重叠部分的面积为 S，请直接写出 S 与 t 之间的函数关系式以及自变量 t 的取值范围. 附加：（A 卷）如图，在矩形 ABCD 中，E,F 为 AD,BC 上的点，且 ED=BF，连接 EF 交对角线 BD 于点 O，连接 CE，且 CE=CF,  EFC (1)求证：FO=EO.  2 DBC . (2)若 CD= 32 ，求 BC 的长.

资料库

2013年重庆市中考数学真题B卷.doc

相关推荐

中考

热门标签

最新资料