第1页 / 共4页
第2页 / 共4页
第3页 / 共4页
第4页 / 共4页
Enhancement of speech corrupted by acoustic noise.pdf
ENHANCEMENT OF SPEECH CORRUPTED BY ACOUSTIC NOISE*
M. Berouti, R. Schwartz, and J. Makhoul
Bolt Beranek and Newman Inc.
Cambridge, Mass.
ABSTRACT
This paper describes a method for enhancing
speech corrupted by broadband noise. The method is
based on the spectral noise subtraction method.
The original method entails subtracting an estimate
of the noise power spectrum from the speech power
spectrum, setting negative differences to zero,
recombining the new power spectrum with the
original phase, and then reconstructing the time
waveform. While this method reduces the broadband
noise, it also usually introduces an annoying
"musical noise". We have devised a method that
eliminates this "musical noise" while further
reducing the background noise. The method consists
in subtracting an overestimate of the noise power
and preventing the resultant spectral
spectrum,
components from going below a preset minimum level
(søectral floor).
The method can automatically
adapt to a wide range of signal—to—noise ratios, as
long as a reasonable estimate of the noise spectrum
can be obtained. Extensive listening tests were
quality and
performed
intelligibility of speech enhanced by our method.
Listeners unanimously preferred the quality of the
processed speech.
input
signal—to—noise ratio of 5 dB, there was no loss of
intelligibility associated with the enhancement
technique.
determine
Also,
for
an
to
the
1. INTRODUCTION
We report on our work to enhance the quality
of speech degraded by additive white noise. Our
goal is to improve the listenability of the speech
signal by decreasing the background noise, without
affecting the intelligibility of the speech.
The
noise is at such levels that the speech is
essentially unintelligible out of context. We use
the average segmental signal—to—noise ratio (SNR)
to measure the noise level of the noise—corrupted
speech signal. We found that sentences with a SNR
in the range —5 to +5 dB have an intelligibility
score in the range 20 to 80%. There is strong
correlation between the intelligibility of a
sentence and the SNR, but intelligibility also
depends on the speaker, on context, and on the
phonetic content.
After an initial investigation of several
methods of speech enhancement, we concluded that
the method of spectral noise subtraction is more
effective than others. In this paper we discuss
our implementation of that method, which differs
* An earlier version of' this paper was presented at
the ARPA Network Speech Compression (NSC) Group
meeting, Cambridge, MA, May 1978, in a special
session on speech enhancement.
CHl37Y—7/7/OOQ0—O201)O.T5 ©1w79 TELE
208
from that reported by others in two major ways:
first, we subtract a factor (a) times the noise
spectrum, where a is a number greater than unity
and varies from frame to frame. Second, we prevent
the spectral components of the processed signal
from going below a certain lower bound which we
call the sceotral floor. We express the spectral
floor as a fraction , of the original noise power
spectrum Pn(w).
2. BASIC METHOD
The
basic
However, taking this assumption as
principle of spectral noise
subtraction appears in the literature in various
implementations [1_1]. Basically, most methods of
speech enhancement have in common the assumption
that the power spectrum of a signal corrupted by
uncorrelated noise is equal to the sum of the
The
signal spectrum and the noise spectrum.
preceding statement is true only in the statistical
sense.
a
reasonable approximation for short—term (25 as)
spectra, its application leads to a simple noise
subtraction method.
Initially, the method we
implemented consisted in computing the power
spectrum of each windowed segment of speech and
subtracting from it an estimate of the noise power
spectrum. The estimate of the noise is formed
during periods of "silence". The original phase of
the OFT of the input signal is retained for
the enhancement algorithm
resynthesis.
consists of a straightforward implementation of the
following relationship:
Thus,
let D(w) = P5(w)—P0(w)
ID(v), if D(w)>O
P(w) 0, otherwise
(1)
where P(w) is the modified signal spectrum, P5(w)
is the spectrum of the input noise—corrupted
speech, and Pn(w) is the smoothed estimate of the
Pn(w) is obtained by a two—step
noise spectrum.
process: First we average the noise spectra from
several frames of "silence". Second, we smooth in
frequency this average noise spectrum.
For the
specific case of white noise, the smoothed estimate
of the noise spectrum is flat. The enhanced speech
signal is obtained from both P(w) and the original
phase by an inverse Fourier transform:
s'(t) = F{)
(2)
where 0(w) is the phase function of the DFT of the
input speech. Since the assumption of uncorrelated
signal and noise is not strictly valid for
short—term spectra, some of the components of the
processed spectrum, P(w), may be negative.
These
negative values are set to zero as shown in (1).
A major problem with the above implementation
of the spectral noise subtraction method has been
that a "new" noise appears in the processed speech
signal. The new noise is variously described as
of tonal quality, or
ringing,
"doodly—doos". We shall henceforth refer to it as
Also, though the noise is
the "musical noise".
reduced, there is still considerable broadband
noise remaining in the processed speech.
warbling,
3. NATURE OF THE PROBLEM
To explain the nature of the musical noise,
one must realize that peaks and valleys exist in
the short—term power spectrum of white noise; their
frequency locations for one frame are random and
they vary randomly in frequency and amplitude from
When we subtract the smoothed
frame to frame.
estimate of the noise spectrum from the actual
noise spectrum, all spectral peaks are shifted down
while the valleys (points lower than the estimate)
are set to zero (minus infinity on a logarithmic
scale). Thus, after subtraction there remain peaks
in the noise spectrum. Of those remaining peaks,
the wider ones are perceived as time varying
The narrower peaks, which are
broadband noise.
relatively large spectral excursions because of the
deep valleys that define them, are perceived as
time varying tones which we refer to as musical
noise.
. PROPOSED SOLUTION
Our modification to the noise subtraction
method consists in minimizing the perception of the
narrow spectral peaks by decreasing the spectral
excursions. This is done by changing the algorithm
in (1) to the following:
let D(w) = P5(w) -aP0(w)
P'(w)
S
D(w), i± D(w)>BP0(w)
Lpn(), otherwise
with al, and O<<1. For n>1 the remnants of the noise peaks
will be lower relative to the case with 0=1. Also,
with 0>1 the subtraction can remove all of the
broadband noise by eliminating most of the wide
However, this by itself is not sufficient,
peaks.
because the deep valleys surrounding the narrow
peaks remain in the noise spectrum and, therefore,
the excursion of noise peaks remains large. The
second part of our modification consists of
"filling—in" the valleys. This is done in (3) by
means of the soectral floor, P(w): The spectral
components of P(w) are prevented from descending
below the lower bound P0(w). For >O, the valleys
between peaks are not as deep as for the case B=O.
Thus, the spectral excursion of noise peaks is not
as large, which reduces the amount of the musical
noise perceived. Another way to interpret the
above is to realize that, for >O, the remnants of
noise peaks are now "masked" by neighboring
spectral components of comparable magnitude. These
neighboring components in fact are broadband noise
reinserted in the spectrum by the spectral floor
Pn(w). Indeed, speech processed by the modified
method has less musical noise than speech processed
by (1). We note here that for <<1 the added
broadband noise level is also much lower than that
perceived in speech processed by (1).
In order to be able to refer to the "broadband
noise reduction" achieved by the method, we have
conveniently expressed the spectral floor as a
fraction of the original noise power spectrum.
Thus, when the spectral floor effectively masks the
musical noise, and when all that can be perceived
is broadband noise, then the noise attenuation is
given by . For instance, for =O.O1, there is a
20 dB attenuation of the broadband noise.
Various combinations of a and give rise to a
trade—off between the amount of remaining broadband
noise and the level of the perceived musical noise.
For large, the spectral floor is high, and very
little, if any, musical noise is audible, while
with
small, the broadband noise is greatly
reduced, but the musical noise becomes quite
annoying. Similarly, we have found that, for a
fixed value of , increasing the value of a reduces
both the broadband noise and the musical noise.
However, if a is too large the spectral distortion
caused by the subtraction in (3) becomes excessive
and the speech intelligibility may suffer.
In practice, we have found that at SNR=0 dB, a
value of a in the range 3 to 6 is adequate, with
in the range 0.005 to 0.1. A large value of 0,
such as 5, should not be alarming. This is
equivalent to assuming that the noise power to be
subtracted is about 7 dB higher than the smoothed
This "inflation" factor represents the
estimate.
fact that, at each frame, the variance of the
spectral components of the noise is equal to the
noise power itself. Hence, one must subtract more
than the expected value of the noise spectrum (the
smoothed estimate) in order to make sure that most
of the noise peaks have been removed.
In order to reduce the speech distortion
caused by large values of a, we decided to let a
vary from frame to frame within the same sentence.
To understand the rationale behind doing so,
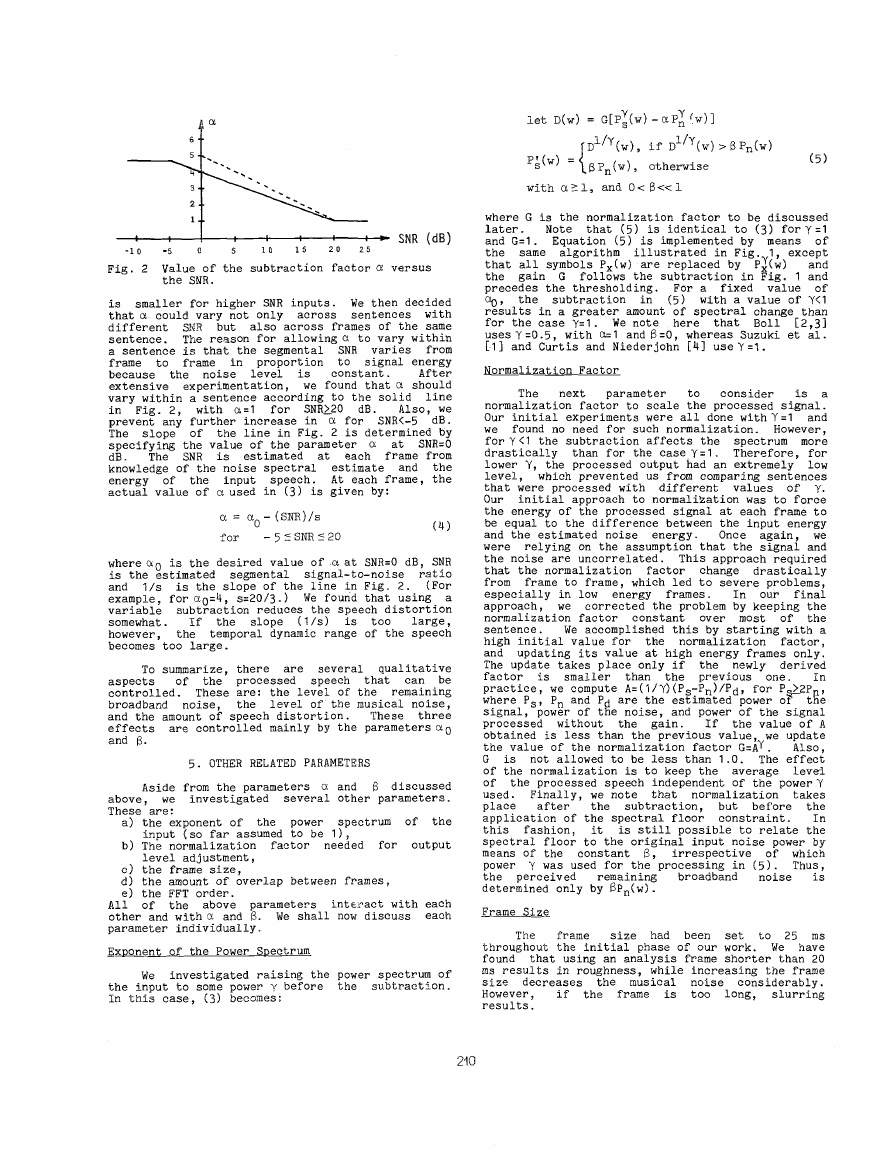
consider the graph of Fig. 2. The dotted line in
the figure shows a plot of the value of a used in
an experiment where several sentences at different
SNR were proceased. In the experiment, a was
constant for each utterance. At the completion of
the experiment, we noticed that the optimal value
of a, as determined empirically for best noise
reduction with the least amount of musical noise,
209
:
2
0
5
10
15
20
25
SNR (dB)
-10
—5
Fig. 2 Value of the subtraction factor a versus
the SNR.
is smaller for higher SNR inputs. We then decided
that a could vary not only across sentences with
different SNR but also across frames of the same
sentence. The reason for allowing a to vary within
a sentence in that the segmental SNR varies from
frame to frame in proportion to signal energy
because the noise level is constant.
After
extensive experimentation, we found that a should
vary within a sentence according to the solid line
Also, we
in Fig. 2, with an
prevent any further increase in a for SNR<.-5 dB.
The slope of the line in Fig. 2 is determined by
specifying the value of the parameter a at SNRO
The SNR is estimated at each frame from
dB.
knowledge of' the noise spectral estimate and the
energy of the input speech. At each frame, the
actual value of' a used in (3) is given by:
for SNR20 dB.
a =
for —5fSNRt2O
a0—(SNB)/s
(14)
where 00 is the desired value of a at SNR=0 dB, SNR
is the estimated segmental signal—to—noise ratio
and 1/s is the slope of the line in Fig. 2. (For
example, for a0=4, sr2O/3.) We found that using a
variable subtraction reduces the speech distortion
If the slope (1/s) is too large,
somewhat.
however, the temporal dynamic range of the speech
becomes too large.
To summarize, there are several qualitative
aspects of the processed speech that can be
controlled. These are: the level of the remaining
broadband noise, the level of the musical noise,
and the amount of speech distortion. These three
effects are controlled mainly by the parameters a0
and 13.
5. OTHER RELATED PARAMETERS
Aside from the parameters a and 13 discussed
above, we investigated several other parameters.
These are:
a) the exponent of' the power spectrum of' the
b) The normalization factor needed for output
input (so far assumed to be 1),
level adjustment,
o) the frame size,
d) the amount of overlap between frames,
e) the FFT order.
All of the above parameters interact with each
other and with a and 13. We shall now discuss each
parameter individually.
Exoonent of the Power Soectrwi
We investigated raising the power spectrum of
the input to some power -y before the subtraction.
In this case, (3) becomes:
let D(w) = G[P(w)-aPw)]
P(w)
if
with al, ani3. 0<13<
Window OverlaiD
Associated with the frame size is the amount
of overlap between consecutive frames. We have
used the Tukey window (flat in its middle range and
with cosine tapering at each end) in order to
overlap and add adjacent segments of processed
The overlap is necessary to prevent
speech.
discontinuities at frame boundaries. The amount of
overlap is usually taken to be 10% of the frame
10% may be
size. However, for larger frames,
excessive and might cause slurring of the signal.
FFT Order
The third window—related parameter is the
order of the FFT. In general, enough zeros are
appended at one end of the windowed data prior to
obtaining the DFT, such that the total number of
points is a power of 2 and, thus, an FFT routine
can be used. However, processing in the frequency
domain causes the non—zero valued data to extend
out of its original time—domain range into the
added zeros. If the added—zero region is not long
enough, time-domain aliasing might occur. Thus we
needed to investigate adding more zeros and using a
higher order FFT.
6. EXPERIMENTS AND RESULTS
The discussions in Sections 3 and shed some
light on the effect that each parameter has on the
We performed
quality of the processed speech.
several experiments to understand further how all
these parameters interact.
We were mainly
interested in finding an optimal range of values
for a0 and 6.
As mentioned earlier, these two
parameters give us direct control of the three
major qualitative aspects of processed speech:
remaining broadband noise, musical noise, and
speech distortion. Clearly, we desire values of a0
and 6 that would minimize those three effects.
However, the effects of the parameters c and 6 on
the quality of the processed speech are intimately
related to the input SNR, the power y, and the
window—related parameters.
Throughout our experiments, we considered
inputs with SNR in the range —5 to ÷5 dB and used
values of yrO.25, 0.5, and 1. We have experimented
with several frame sizes (15 to 60 ms), different
amounts of overlap between frames, and different
FFT orders.
Through
extensive
and 35 ms.
experimentation
we
determined the range of values for each of the
parameters of the algorithm. The ranges given
below are meant to be guidelines rather than final
Optimality is a subjective
"optimal" values.
choice and depends on the user's preference. Below
we give some of the conclusions we reached:
— Frame size: The frame size should be between 25
— Overlap: The overlap between frames should be on
the order of 2 to 2.5 ms.
— FFT order: Our investigations
did not show that
time—domain aliasing was an important issue.
Therefore, the minimum FFT order corresponding to
a given frame size is adequate,
with no
noticeable improvement in going to a higher
order. The same was reported earlier by Boll
[2].
— Exponent of the power spectrum: Of the three
values of y we tried, Y1 was found to yield
better output quality, in general.
— Subtraction factor: for yrl, an optimal range for
a0 is 3 to 6 (for yr.5, a0 should be in the range
2 to 2.2). The slope in () (or Fig. 2) is set
dB.
such that c1 for SNR20 dB, and ao0 at SNR=O
— Spectral floor: The spectral floor depends on the
average segmental SNR of the input, i.e., the
noise level. For high noise levels (SNR—5 dB) 6
should be in the range 0.02 to 0.06, and for
lower noise levels (SNRO or +5 dB) 6 should be
in the range 0.005 to 0.02.
Towards the end of our research we performed a
formal listening test to assess the quality and
intelligibility of the enhanced speech. The input
speech varied in SNE from —5 to +5 dB. The
processing was done using parameter values as given
by the above guidelines. Subjects unanimously
preferred the quality of the enhanced speech to
that of the unprocessed signal.
In addition, at
input SNR=+5 dB, using the values
6=.0O5,
Yrl, and a 32 ma frame size, the intelligibility of
the enhanced speech was the same as that of the
For lower SNR's, the
unprocessed signal.
intelligibility of the speech decreased somewhat,
Prior to performing the formal intelligibility
test, our algorithm had been tuned for optimal
quality, i.e., maximum noise reduction, without
accurate knowledge of the effect of the method on
speech intelligibility. We believe that it may be
possible to maintain the same intelligibility while
improving the listenability of the speech by
further tuning the parameters of the system (mainly
a0 and 6). The actual parameter values used in a
specific situation depend on one's purpose in using
the enhancement algorithm. In some applications a
slight loss of intelligibility may be tolerable,
provided the listenability of the speech is greatly
improved. In other applications a
loss in
intelligibility may not be acceptable.
7. CONCLUSIONS
To conclude, the main differences between the
basic spectral subtraction method and our
implementation is that we subtract an overestimate
of the noise spectrum and prevent the resultant
spectral components from going below a ectral
floor. Our implementation of the spectral noise
subtraction method affords a great reduction in the
background noise with very little effect on the
intelligibility of the speech. Formal tests have
shown that, at SNR=+5 dB, the intelligibility of
the enhanced speech is the same as that of the
unprocessed signal.
ACKNOWLEDGMENTS
The authors wish to thank A.W.F. Huggins for
his contributions to this research. This work was
sponsored by the Department of Defense.
REFERENCES
1. H. Suzuki, J.
Y. Ishii,
"Extraction of Speech in Noise by Digital
Filtering," J. Acoust. Soc. of Japan, Vol. 33,
No. 8, Aug. 1977, pp. 1O5—411.
Igarashi,
2. 5. Boll, "Suppression of Noise in Speech Using
the SABER Method," ICASSP, April 1978, pp.
606—609.
and
3. S. Boll, "Suppression of Acoustic Noise in
Speech Using Spectral Subtraction," submitted,
IEEE Trans. on Acoustics, Speech and Signal
Processing.
1. R.A. Curtis, R.J. Niederjohn, "An Investigation
of
Several Frequency—Domain Methods for
Enhancing the Intelligibility of Speech in
Wideband Random Noise," ICASSP, April 1978, pp.
602—605.
21
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
