matlab 多元线性回归.pdf-资料库

Matlab 多元线性回归 1、多元线性回归在回归分析中，如果有两个或两个以上的自变量，就称为多元回归。事实上，一种现象常常是与多个因素相联系的，由多个自变量的最优组合共同来预测或估计因变量，比只用一个自变量进行预测或估计更有效，更符合实际。在实际经济问题中，一个变量往往受到多个变量的影响。例如，家庭消费支出，除了受家庭可支配收入的影响外，还受诸如家庭所有的财富、物价水平、金融机构存款利息等多种因素的影响，表现在线性回归模型中的解释变量有多个。这样的模型被称为多元线性回归模型。（multivariable linear regression model ）多元线性回归模型的一般形式为： Y = + X + X + + X + , =1,2, i β β β 2 β μ i i i 2 i 1 ki 0 1 k n , （1）其中 k 为解释变量的数目， ( j β = 称为回归系数（regression coefficient)。上 1,2, k , ) j 式也被称为总体回归函数的随机表达式。它的非随机表达式为： , Y = + X + X + + X , =1,2, i β β β 2 β k i i 1 ki 0 1 2 i n jβ 也被称为偏回归系数（partial regression coefficient)。 2、多元线性回归计算模型 Y= + β β β + x 1 1 x 2 2 0 + + β ε ε + , x k k ∼ N (0, 2 δ ) （2）（3）多元性回归模型的参数估计，同一元线性回归方程一样，也是在要求误差平方和（Σe) 为最小的前提下，用最小二乘法或最大似然估计法求解参数。 x 设 11 ( , x 12 , , x 1 p , y 1 ), , ( x n 1 , x n 2 , , x np , y n ) 是一个样本，用最大似然估计法估计参数： ˆ ˆ b b , 取 0 1 , , ˆ b p , 当 b 0 = ˆ b b 0 1 , = ˆ b 1 , , b p = ˆ b p Q 时， = 达到最小。 n ∑ i 1 = ( y i − b 0 − b x i 1 1 − − b x p ip 2 ) ⎧ ∂ Q ⎪ ∂⎪ b 0 ⎨ ∂⎪ Q b ⎪ ∂⎩ j j 1,2, = （4）化简可得： 2 = − 2 = − n i n 1 = ( ∑ ∑ 1 = p , i ( y i − b 0 − b x i 1 1 − − b x p ip ) 0, = y i − b 0 − b x i 1 1 − − b x p ip ) x ij = 0 （4）

b n b + 0 1 n ∑ i 1 = x i 1 + b 2 n ∑ i 1 = x i 2 + + b p n ∑ i 1 = x ip = y i , n ∑ i 1 = x 2 i 1 + b 2 n ∑ 1 = x x i i 1 2 + + b p x x i ip 1 b 0 b 0 n ∑ i 1 = n ∑ i 1 = x i 1 + b 1 x ip + b 1 = x y i i 1 , i n ∑ 1 = i n ∑ 1 = i n ∑ i 1 = （5） ⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎬ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎭ n ∑ i 1 = x x ip i 1 + b 2 n ∑ i 1 = x x ip i 2 + + b p n ∑ i 1 = x 2 ip = 引入矩阵： n ∑ i 1 = x y ip i . x 11 x 21 x n 1 方程组（5）可以化简得： 1 1 1 ⎛ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ X = x 12 x 22 x n 2 p p x 1 x 2 x np , Y = ⎞ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ X XB X Y ' = ' y 1 y 2 y n ⎞ ⎟ ⎟ ⎟ ⎟ ⎠ , B = b 0 b 1 b p ⎛ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎞ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ . （6） ⎛ ⎜ ⎜ ⎜ ⎜ ⎝ 可得最大似然估计值： ˆ B = ˆ b 0 ˆ b 1 ˆ b p ⎛ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎞ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ = ( X X ' ) 1 − X Y ' ( μ x x , 1 2 , , x )p = b 0 + b x 1 1 + + b x p p 的估计是： ˆ y = ˆ b 0 + ˆ b x 1 1 + ˆ b x 2 2 + + ˆ b x p p 公式（8）为 P 元经验线性回归方程。 3、 Matlab 多元线性回归的实现多元线性回归在 Matlab 中主要实现方法如下：（1）b=regress(Y, X ) 确定回归系数的点估计值其中（7）（8） X = 1 1 1 ⎛ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ x 11 x 21 x n 1 x 12 x 22 x n 2 p p x 1 x 2 x np , Y = ⎞ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎛ ⎜ ⎜ ⎜ ⎜ ⎝ y 1 y 2 y n ⎞ ⎟ ⎟ ⎟ ⎟ ⎠ , B = b 0 b 1 b p ⎛ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎞ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ . (9)

（2）[b,bint,r,rint,stats]=regress(Y,X,alpha) 求回归系数的点估计和区间估计、并检验回归模型 ①bint 表示回归系数的区间估计. ②r 表示残差 ③rint 表示置信区间 ④stats 表示用于检验回归模型的统计量,有三个数值：相关系数 r2、F 值、与 F 对应的概率 p 说明：相关系数 r2 越接近 1，说明回归方程越显著；F>F1-alpha(p,n-p-1) 时拒绝 H0，F 越大，说明回归方程越显著；与 F 对应的概率 p<α 时拒绝 H0，回归模型成立。 ⑤alpha 表示显著性水平(缺省时为 0.05) （3）rcoplot(r,rint) 画出残差及其置信区间实例 1：（一元线性回归）测得 16 名女子的身高和腿长如下表所示（单位:cm）：身高 143 145 腿长 88 85 身高 155 156 腿长 96 98 146 88 157 97 147 91 158 96 149 92 159 98 150 93 160 99 153 93 162 100 154 95 164 102 试研究这些数据之间的关系。分析： x=[143,145,146,147,149,150,153,154,155,156,157,158,159,160,162,164] 由式（9）可得 X=[eT, xT]（eT 为单位列向量） y=[88,85,88,91,92,93,93,95,96,98,97,96,98,99,100,102] Y= yT Matlab 程序为： /输入如下命令：/ x=[143,145,146,147,149,150,153,154,155,156,157,158,159,160,162,164]; y=[88,85,88,91,92,93,93,95,96,98,97,96,98,99,100,102]; X=[ones(length(y),1),x']; Y=y'; [b,bint,r,rint,stats]=regress(Y,X); b,bint,stats 在 Matlab 图示所示：

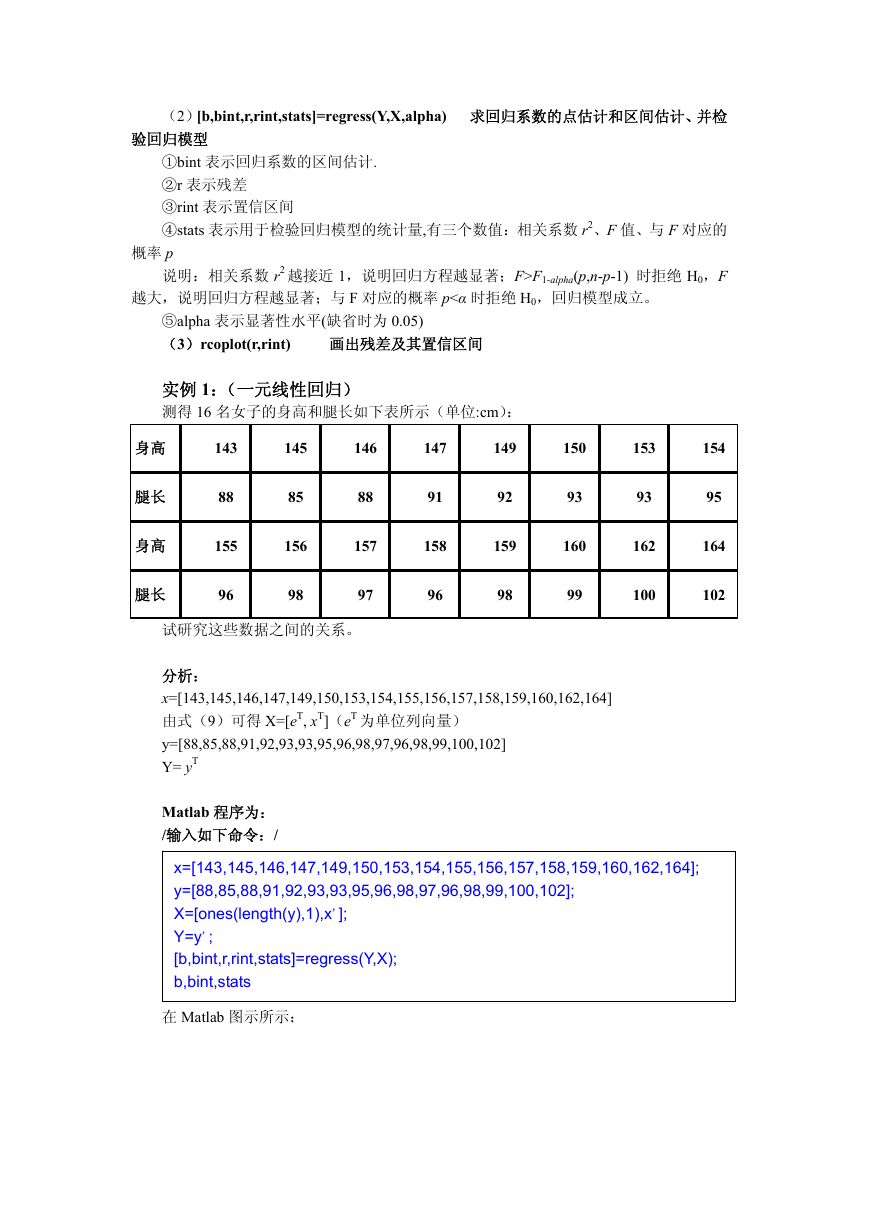
/输出结果如图所示：/ ˆ b 因此我们可得 0 ˆ b 1 = − = 16.0730, 0.7194. ˆ b ， 0 的置信区间 ( 33.7071,1.5612), − ˆ b 的置信区间 1 (0.6047, 0.834). 2 r = 0.9282, F = 180.9531, p = 0.0000. < = − 回归模型 0.05, 16.0730 0.7194 p y /残差分析/ 在 Matlab 命令窗口输入 + x . 成立 rcoplot(r,rint) 得到残差图如图所示：

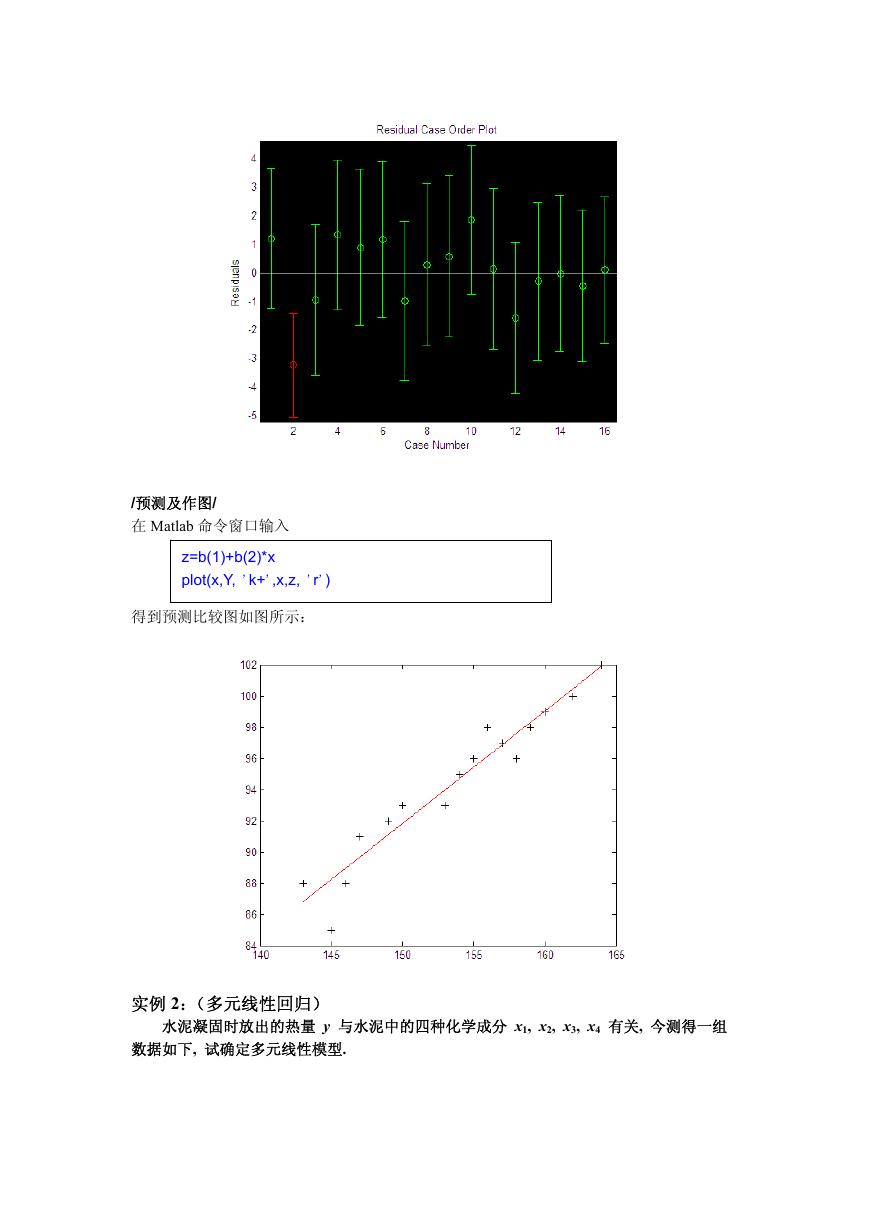
/预测及作图/ 在 Matlab 命令窗口输入 z=b(1)+b(2)*x plot(x,Y, 'k+',x,z, 'r') 得到预测比较图如图所示：实例 2：（多元线性回归）水泥凝固时放出的热量 y 与水泥中的四种化学成分 x1, x2, x3, x4 有关, 今测得一组数据如下, 试确定多元线性模型.

序号 x1 x2 x3 x4 y 序号 x1 x2 x3 x4 y 1 7 26 6 60 78.5 8 1 31 22 44 72.5 2 1 29 15 52 74.3 9 2 54 18 22 93.1 3 11 56 8 20 104.3 10 21 47 4 26 115.9 4 11 31 8 47 87.6 11 1 40 23 34 83.8 5 7 52 6 33 95.9 12 11 66 9 12 113.3 6 11 55 9 22 109.2 13 10 68 8 12 109.4 7 3 71 17 6 102.7 分析： x1=[7,1,11,11,7,11,3,1,2,21,1,11,10]; x2=[26,29,56,31,52,55,71,31,54,47,40,66,68]; x3=[6,15,8,8,6,9,17,22,18,4,23,9,8]; x4 =[60,52,20,47,33,22,6,44,22,26,34,12,12]; y=[78.5,74.3,104.3,87.6,95.9,109.2,102.7,72.5,93.1,115.9,83.8,113.3,109.4]; 由式（9）可得 X=[eT, x1 Y= yT Matlab 程序为： /输入如下命令：/ T]（eT 为单位列向量） T, x4 T, x2 T, x3 x1=[7,1,11,11,7,11,3,1,2,21,1,11,10]; x2=[26,29,56,31,52,55,71,31,54,47,40,66,68]; x3=[6,15,8,8,6,9,17,22,18,4,23,9,8]; x4 =[60,52,20,47,33,22,6,44,22,26,34,12,12]; y=[78.5,74.3,104.3,87.6,95.9,109.2,102.7,72.5,93.1,115.9,83.8,113.3,109.4]; X=[ones(length(y),1),x1',x2',x3',x4']; %把行向量转轶为列向量 Y=y'; %把行向量转轶为列向量 [b,bint,r,rint,stats]=regress(Y,X); b,bint,stats 在 Matlab 图示所示：

/输出结果如图所示：/ 因此我们可得 ˆ b 0 ˆ b 1 ˆ b 2 ˆ b 3 ˆ b 4 = = = = = − 62.4054, 1.5511, 0.5102, 0.1019, 1441. ， ˆ b 0 ˆ b 1 ˆ b 2 ˆ b 3 ˆ b 4 ( 99.1786, 223.9893), − ( 0.1663, 3.2685), − ( 1.1589, 2.1792), − ( 1.6385,1.8423), − ( 1.7791,1.4910). − 的置信区间的置信区间的置信区间的置信区间的置信区间 2 r = 0.9824, F = 111.4792, p = 0.0000. p y < = − 回归模型 0.05, x 62.4054 1.5511 1 + + 0.5102 x 2 . +0.1019 -0.1441 成立 x 4 x 3