ARMA信号预测代码直接使用.docx

发布时间：2022-06-19 发布人：admin 分类：说明书资料大小：0.08M 资料格式：docx 举报版权申诉

89605793-3f25-49fc-a722-90a3864df53a.docx.pdf-第1页.png

第1页 / 共5页

89605793-3f25-49fc-a722-90a3864df53a.docx.pdf-第2页.png

第2页 / 共5页

89605793-3f25-49fc-a722-90a3864df53a.docx.pdf-第3页.png

第3页 / 共5页

89605793-3f25-49fc-a722-90a3864df53a.docx.pdf-第4页.png

第4页 / 共5页

89605793-3f25-49fc-a722-90a3864df53a.docx.pdf-第5页.png

第5页 / 共5页

文本预览

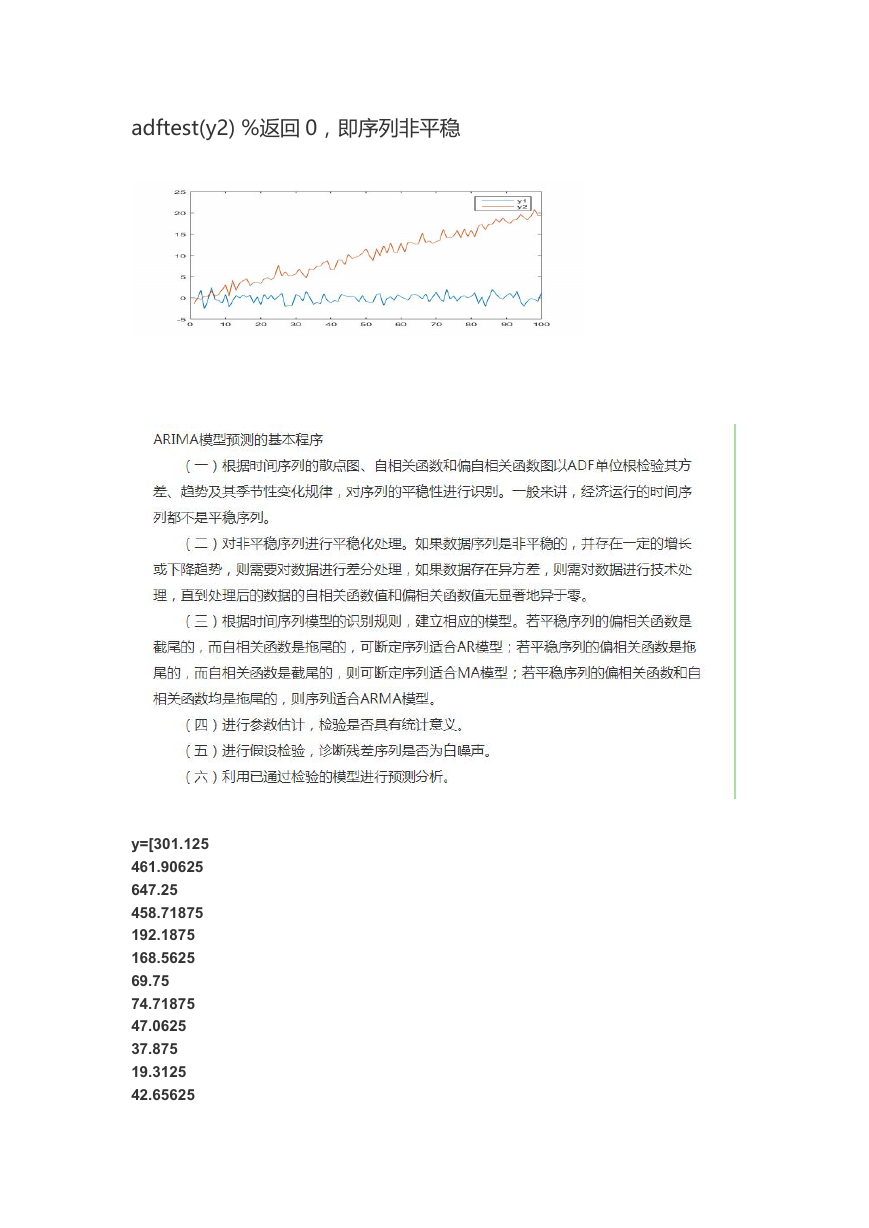
z=xlsread('F:\46.xls','A1:A1486'); y=iddata(z); m=armax(y(1:1480),'na',5,'nc',3); p=predict(m,y,1); figure plot(y(1481:1486),p(1481:1486)); %取得存在 excell 里的测量数据 1486 个 %转换到频域 %使用模型进行分析,这里系数分别为 5,3 %预测 1. 检测数值模拟的信号的平稳性检验一个时间序列是否平稳，用 ADF 检验，在 matlab 中是 adftest( ) 函数，最简单的用法就是 h = adftest(Y)，其中 Y 为待检验序列，返回值 h=1 表示序列平稳， h=0 表示非平稳。比如 %构造两个序列进行检测 t = (1:100)'; y1 = randn(100,1); %平稳序列 y2 = randn(100,1) + .2*t; %非平稳序列 plot(t,y1,t,y2); adftest(y1) %返回 1，即序列平稳

adftest(y2) %返回 0，即序列非平稳 y=[301.125 461.90625 647.25 458.71875 192.1875 168.5625 69.75 74.71875 47.0625 37.875 19.3125 42.65625

38.8125 23.34375 93 46.125 2.8125 0 0 0 0 0 16.78125 20.4375 31.96875 23.8125 37.96875 17.8125 68.8125 321 227.71875 143.71875 144.46875 148.21875 150.1875 146.625 ]; Data=y; SourceData=Data(1:24,1); step=12; TempData=SourceData; TempData=detrend(TempData);%消除时间序列中的线性趋势项 TrendData=SourceData-TempData; %--------差分，平稳化时间序列--------- H=adftest(TempData); difftime=0; SaveDiffData=[]; while ~H SaveDiffData=[SaveDiffData,TempData(1,1)]; TempData=diff(TempData); %差分，平稳化时间序列 difftime=difftime+1; %差分次数 H=adftest(TempData); %adf 检验，判断时间序列是否平稳化 end %---------模型定阶或识别-------------- u = iddata(TempData); test = [];

for p = 0:5 %自回归对应 PACF,给定滞后长度上限 p 和 q，一般取为 T/10、ln(T)或 T^(1/2), 这里取 T/10=12 for q = 0:5 %移动平均对应 ACF m = armax(u,[p q]); AIC = aic(m); %armax(p,q),计算 AIC test = [test;p q AIC]; end end for k = 1:size(test,1) if test(k,3) == min(test(:,3)) %选择 AIC 值最小的模型 p_test = test(k,1); q_test = test(k,2); break; end end %------1 阶预测----------------- TempData=[TempData;zeros(step,1)]; n=iddata(TempData); m = armax(u,[p_test q_test]); %m = armax(u(1:ls),[p_test q_test]); %armax(p,q),[p_test q_test]对应 AIC 值最小，自动回归滑动平均模型 P1=predict(m,n,1); PreR=P1.OutputData; PreR=PreR'; %----------还原差分----------------- if size(SaveDiffData,2)~=0 for index=size(SaveDiffData,2):-1:1 PreR=cumsum([SaveDiffData(index),PreR]); end end %-------------------预测趋势并返回结果---------------- mp1=polyfit([1:size(TrendData',2)],TrendData',1); xt=[]; for j=1:step xt=[xt,size(TrendData',2)+j]; end TrendResult=polyval(mp1,xt); PreData=TrendResult+PreR(size(SourceData',2)+1:size(PreR,2)); tempx=[TrendData',TrendResult]+PreR; % tempx 为预测结果 plot(tempx,'r'); hold on plot(Data,'b') legend('预测输出','期望输出')

分享到：

赞收藏

资料库

ARMA信号预测代码直接使用.docx

相关推荐

人工智能

热门标签

最新资料